Three Dimensional Numerical Analysis of Two Phase Flow Separation Using Swirling Fluidics ()
1. Introduction
Boiling water reactors (BWRs) are equipped with steam separators for splitting a two-phase mixture into steam and water before feeding the steam to dryers and turbines [1]. Steam separators are used to remove water from steam in a BWR. In the separator, a two phase flow of steam-water mixture rises through the stand pipes to strike vanes which give the mixture a swirl, forming a vortex where centrifugal forces form a vortex and where centrifugal forces separate the water from the steam in the barrel. An annular two phase dispersed flow is occurred there. The steam including the water droplets, leave the separator at the top and goes into the dryers. The separated water rises long the inside wall of the barrels, flows through pick-off rings, and exits from the discharge passages through the pick off rings. When upgrading the power density of BWR core, one of the technical issues we have to deal with is the improvement of the steam separators. Since the upgrading causes the increase in the steam quality and the flow velocity at the entrance of the steam separator. In the two phase flow regions pressure drop may increase what results in the deterioration of flow stability which is often seen in the conventional separator. Therefore, the steam separator should be improved so as to decrease the pressure drop at high steam qualities without degrading the separator performance.
Hirai and Yokobori have proposed a new two phase flow separation system using swirling fluidics [2]. Utilizing square arrangement of BWR fuel assemblies, twophase separation is achieved by adding the artificial radial flow divided partially from total axial core flow. The most important characteristic feature is the removal of stationary vane, which is replaced by the fluidics. This concept is applied in the degassing machine in the smoking room. They clarified the thermal-hydraulic behaviors of this swirl motion using small mock-up apparatus. Both water and air were used as atmospheric twophase flow and experiment small-scale test facility was fabricated [3]. They confirmed through the visualizing experiments that the two-phase flow separation was well confirmed along the flow distribution. From the laser sheet plane normal to the main flow direction, four mini scale jets were well mixed and large-scale swirling flow motion was found to be successfully created. Throughout the tests, important parameters such as flow rate, angle, the sub and main flow ratio, void fraction and sub flow axial position were varied. According to these parameter sensitivities, separated behaviors were so stable that two-phase flow was well separated in every test case.
These performances have been estimated in such mock-up tests, however, such tests are of long duration and costly. Therefore, it would be better to develop a numerical method to estimate separator performances so as to develop an innovative separator. In the present study, an idea of low cost simplified innovative separator using lattice core configuration is proposed where swirling is caused by the orthogonal driving flow. The four fuel assemblies around the control rod of BWR, the conventional separator with swirler and the proposed concept of the separator are shown in Figures 1-3, respectively. But the performance of the separator is still needed to be assed. Hence, the objective of the present study is to develop a numerical model to estimate the performance of the proposed separator and to validate the developed model with the experimental results. A three dimensional analysis of steam-water separation has been performed with the commercial numerical analysis code ANSYS FLUENT 14.0 which consists of a three-dimensional two-fluid model [4]. In the analysis, the geometry and flow conditions are chosen according to the experimental study of Hirai [3] who studied experimentally the performance of the vapor-water separation of the proposed model.
2. Steam Water Separation by ANSYS FLUENT 14.0
2.1. Numerical Models
The computational fluid dynamic code, FLUENT 14.0 was used to investigate the 3-D turbulent flow in the cylinder using the standard k − e and the realizable k − e turbulence models. In the calculation a phase–coupled SIMPLE (Semi-Implicit Method for Pressure Linked Equations) algorithm for the pressure-velocity coupling is adopted. The second order upwind schemes were used for the momentum while first order upwind schemes were used for the turbulence kinetic energy, turbulence dissipation rate, and volume fraction. Convergence was assumed when the residual of the equations dropped more than three orders of magnitude. The under relaxation parameters for pressure, momentum, volume fraction, turbulence kinetic energy and turbulence dissipationrate were selected as 0.3, 0.7, 0.5, 0.8 and 0.8,

Figure 1. Four fuel assemblies around the control rod of BWR.

Figure 2. Conventional separator with swirler.
respecttively. Since the flow simulation involved the combined effects of turbulence and two phase flow, the standard k − e and realizable k − e turbulence models are implemented in this study.
2.2. Standard k − ( Model
The standard k − e model [5] is a semi-empirical model based on model transport equations for the turbulence kinetic energy (k) and its dissipation rate (e).

Figure 3. New concept of steam water separator.
The turbulence kinetic energy, k, and its rate of dissipation, e, are obtained from the following transport equations:
 (1)
(1)
and
 (2)
(2)
In these equations,  represents the generation of turbulence kinetic energy due to the mean velocity gradients,
represents the generation of turbulence kinetic energy due to the mean velocity gradients,  is the generation of turbulence kinetic energy due to buoyancy,
is the generation of turbulence kinetic energy due to buoyancy, 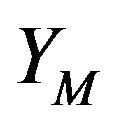 represents the contribution of the fluctuating dilatation in compressible turbulence to the overall dissipation rate,
represents the contribution of the fluctuating dilatation in compressible turbulence to the overall dissipation rate,  ,
,  and
and  are constants.
are constants.  and
and  are the turbulent Prandtl numbers for k and
are the turbulent Prandtl numbers for k and , respectively
, respectively  and
and  are user-defined source terms.
are user-defined source terms.
The turbulent (or eddy) viscosity,  , is computed by combining k and
, is computed by combining k and  as follows:
as follows:
 (3)
(3)
where  is a constant.
is a constant.
The model constants for the standard k − e model are 



 .
.
2.3. Realizable k − ( Model
The realizable k − e model proposed by Shih et al. [6] was intended to address these deficiencies of traditional k–e models by adopting the following:
• A new eddy-viscosity formula involving a variable  originally proposed by Reynolds [7].
originally proposed by Reynolds [7].
• A new model equation for dissipation (e) based on the dynamic equation of the mean-square vorticity fluctuation.
The modeled transport equations for k and in the realizable k − e model are
in the realizable k − e model are
 (4)
(4)
and
 (5)
(5)
where

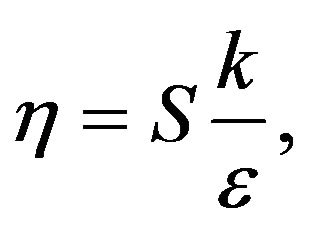

It is to be noted that the k equation in the realizable k–e model is the same as that in the standard k − e model except for the model constants. However, the form of the  equation is quite different from that in the standard k − e model.
equation is quite different from that in the standard k − e model.
The turbulence viscosity is computed from
 (6)
(6)
where
 (7)
(7)
and ,
,  where
where  is the mean rate of rotation tensor viewed in a rotating reference frame with the angular velocity
is the mean rate of rotation tensor viewed in a rotating reference frame with the angular velocity .
.
The model constants  and
and  are given by
are given by
 ,
, 
where 



The model constants for the realizable k − e model are 



2.4. Geometrical Consideration
Figure 4 shows the geometry of the present simulation. The separator has a cylindrical configuration with the diameter of 70 mm and the length of the separator is 300 mm. The fluid is passed from the bottom of the cylinder through the main inlet (inlet1) and the four side inlets. The side inlet is the inlet of the swirling pipe (swirler). Four vertical swirler of polygon in shape has been considered in this analysis. The diameter of the main flow inlet is 10 mm and the diameter of the swirling flow inlet is 2 mm. The length of the swirler is 80 mm.
2.5. Analysis System and Condition
Figure 5 shows the mesh of the analysis system generated by ICEM CFD tool. The mesh is simplified in internal octagonal cylindrical pipe as it is difficult to cut the cylindrical mesh. Nozzle is designed in square shape. Turbulence models have been adopted in the unsteady calculation using Euler method. Non-slip wall, 1 mm bubble diameter was adopted in the analysis.
Water and air velocity of mail flow was 0.3 m/s and

Figure 4. Geometry of the present simulation.

Figure 5. Hexahedron-based mesh for the analysis system.
the swirling driving flow velocity was 1.2 m/s. Inlet void fraction of air in the main flow was 68% where as inlet void fraction of swirling driving flow was 0%. The calculation was performed under the gravitational acceleration of 9.81 m/s2. The time step size, number of time steps and maximum number of iterations per time steps were 0.01s, 2000 and 1000, respectively. The angle of rotation of swirler was 90˚.
3. Results and Discussion
The results of the three dimensional numerical computations of vapor-water two phase flow separation using swirl has been presented in this section. In order to gain confidence of the modeling methodology that is required to adequately simulate the separator flow, the analysis results were compared with the experimental results performed by Hirai [3] using the same conditions. Figure 6 shows the comparison of analysis results performed using standard k − e model and realizable k − e model of air void fraction as a function of horizontal distance from the center of the separator at 40 mm height from the bottom. The experimental result of void fraction is presented in Figure 7. The analysis results indicates that the realizable k − e model predicted the maximum void fraction of

Figure 6. Numerical results of air void fraction as a function of horizontal distance from the center of the separator at 40 mm height from the bottom.

Figure 7. Experimental result of air void fraction as a function of horizontal distance from the center of the separator at 40 mm height from the bottom.
about 69% which was almost the same as input air void fraction (68%) but the void fraction computed by standard k − e model compared well with the experimental results rather than the realizable k − e model. Figures 8 and 9 represent the velocity vector computed by standard k–e model and realizable k − e model, respectively. The velocity vectors clearly indicate the generation of swirl flow for both of the cases. Figure 10 depicted the comparison of contours of volume fraction analyzed by standard k − e model and the realizable k − e model, respecttively with the experimental results. In numerical simulation, the distributions of the volume fractions are evaluated over the cross-sectional plane of the cylindrical separator using the contour maps. The portion shown in warm colors such as red and orange indicate high concentrations compared with those shown in cold colors such as blue and sky blue. It is seen from both of the Figures 8 and 9 that the separator consists of strong

Figure 8. Velocity vector computed by standard k − e model.

Figure 9. Velocity vector computed by realizable k − e model.

Figure 10. Comparison of contours of volume fraction with experiment and analysis.
swirling flow of high velocity around the center and weak swirling flow of low velocity near the wall. The strong swirling flow in the center results in centrifugal forces that propel the liquid phase (water) to the outer free vortex region, where water is collected and reside in the weak swirling intensity region (Figure 9). Thus, pure vapor phase will flow through the exit region (outlet). The higher volume fraction computed by realizable k − e model than the standard k − e model (in Figure 6) is due to the higher centrifugal forces generated at the center of the separator in case of realizable k − e model than that of standard k − e model. The reason is because the realizable k − e model underestimates the turbulence viscosity and overestimates the swirling velocity (Figures 8 and 9). In Figure 10, some discrepancies in flow pattern between the experimental and simulation results are observed which might be due to the turbulence modeling. In the k–e models, the governing equations are averaged in time, thus the detailed bubble behaviors are homogenized. In order to calculate such a detailed behavior of bubbles, more elaborate turbulence model such as large eddy simulation (LES), which does not use time-averaging approach, is needed.
4. Conclusion
The numerical methodology presented herein establishes that the proposed innovative separator has the potentially significant value in effectively separating the vapor-water two phase flow in BWR. The standard k − e turbulence model and realizable k − e turbulence models are able to predict the flow features inside the separator such as void fraction and velocity distribution. The velocity vectors clearly indicate the generation of swirl flow for both of the cases. The results of the numerical simulation were compared with the experimental data and were found in reasonable agreement. The analysis revels that the maximum air void fraction with realizable k − e model was almost the same as input air void fraction but the void fraction computed by standard k − e model compared better with the experimental results than the realizable k − e model. Some discrepancies in flow pattern between the experimental and simulation results are observed which might be due to the difference of nozzle shape. However, a more detailed model is necessary to reach in the final conclusion.
NOTES