Electromagnetic Nature of Nuclear Energy: Application to H and He Isotopes ()
1. Introduction
1.1. Historical Introduction
After one century of nuclear physics, “it is an open secret that the underlying force remains a puzzle” [1]. The parameters of the potential are still determined by fitting to experimental data [2]. No fundamental law of the nuclear interaction exists. The mysterious strong force is comparable to the “phlogiston”, a hypothetical substance qualified as a gratuitous assumption by Lavoisier [3]. In this paper, it is shown that the binding energy of 2H and 4He is obtained only from the equilibrium between electrostatic and magnetic forces in the nucleus. These forces are known since two millenaries, when the Greeks discovered the properties of amber (elektron) able to attract small objects and magnetite (mount Magnetos). Two centuries ago, the electric and magnetic Coulomb’s laws were discovered. Born had noticed “that the smallest particles carry the lightest energy. (···) From Newton’s law, one can derive that the binding energy of two massive bodies is inversely proportional to the distance between them.” Unfortunately he believed that the neutron was an uncharged particle, thus needing “forces of a different type (···) restricted to a very short range” [4]. The strong force hypothesis originated from the fact that the protons would repel one another and the nucleus should therefore fly apart. The attraction between a proton and a neutron seems still to be ignored although the discovery [5] of the magnetic moment of the neutron, showed its electric charges with no net charge.
1.2. Electromagnetic Interactions
The proton attracts a neutron as an electrized pen attracts small neutral pieces of paper. Bound up with a proton, the neutron becomes the deuteron and the induced dipole the deuteron quadrupole. The permanent dipole of an isolated neutron is negligible but a proton induces an electric dipole in a nearby not so neutral neutron. The dipole and polarizability formulas are invalid in the nonuniform electric field between a neutron and a nearby proton. In the deuteron the magnetic interaction is produced by the collinear and opposite spins of the nucleons (Figure 1). The magnetic moments of the neutron and the proton being opposite, their interaction is repulsive in the deuteron.
1.3. Fundamental Constants
The physical constants used are: elementary electric charge e, neutron and proton magnetic moments μn, μp, vacuum electric permittivity ϵ0, magnetic permeability μ0, light speed c or, equivalently, fine structure constant α, proton mass mp, neutron and proton Landé factors gn, gp, proton Compton radius RP. The formulas in the appendix show the conversion between classical electromagnetic formulas to nuclear physics formulas. The usual fundamental constants of the Coulomb’s electromagnetic potential are replaced by the rigorously equivalent nuclear fundamental constants shown in the appendix. The formula αmpc2 is not “an arbitrary manipulation of the fine structure constant α together with the proton mass”: it shows an interesting similarity with the Hartree constant (twice the Rydberg constant), RH =α2mec2.
2. Assumptions and Approximations
2.1. No Orbital Angular Momentum of the Nucleons
Although a nucleus may rotate as a solid, the nucleons cannot orbit like planets around the sun because the nucleus has no nucleus. Without orbiting nucleons, there is no kinetic energy and the binding energy is indeed the minimum of the electromagnetic interaction potential energy. Quantum mechanics intervenes only via the nucleon spins generating the nucleon magnetic moments. No Schrödinger equation, only electrostatics and magnetostatics.
2.2. No Hypothetical Strong Force
The nuclear interaction is usually assumed to be a mysterious strong force because the corresponding model is assumed to be similar to that of the Bohr atom where a centrifugal force exists. To equilibrate it in the nucleus, a new force named “strong force” was imagined around 70 years ago. A nucleus having no nucleus, the centrifugal force is problematic; therefore, in this paper this assumption is not used. Without centrifugal force, electric and magnetic Coulomb’s forces are strong enough to bind the nucleus as it will be shown below. Contrarily to the mainstream hypothesis, a strong force is not needed to calculate the binding energy of a nucleus. In fact, it is impossible because the physical laws of the strong force are unknown.
2.3. No Empirical Polarizability, Permanent Dipole or Multipole Expansion
Considering electric elementary point charges +e in the proton, +e and −e in the neutron and the original electric Coulomb’s law in 1/r is preferred, instead of empirical concepts derived from it (polarizability and dipoles vary in a non uniform electric field).
2.4. Magnetic Moments
Magnetic moments attract or repulse themselves as can be seen by manipulating magnets, depending on their orientation. In the deuteron, they are opposite as it is well known. In the α particle, the proton magnetic moments are collinear and opposite; they are inclined at 60˚ with respect to the neutron-proton edges of the 4He tetrahedron. Same thing for the neutron magnetic moments. The magnetic moments of paired identical nucleons are here assumed to be collinear and opposite, repulsing themselves, stabilized by the gyroscopic effect.
2.5. Mainly Neutron-Proton Bonds
The only bond of the deuteron is a neutron-proton bond. In A = 3 nuclides, the neutron-proton magnetic interaction, being almost zero, is replaced by the nn or pp repulsion. In the α particle, where there are four np bonds, the single nn and pp bonds may be neglected in a first approximation.
2.6. Nuclear Structure
The proton attracts the negative charge of the neutron and repulses the positive charge of the neutron. According to the electric Coulomb’s law in 1/r2, the positive charge is farther away from the proton than the negative charge. Therefore the repulsion of the positive charge is smaller than the attraction of the negative charge, resulting in a net attraction of the neutron by the proton. In order to obtain an analytical formula for the binding energy, the positive charge of the neutron is neglected in this paper, with an error of around 30% [7] (4% when positive charge taken into account [8]). In 4He, the electric and magnetic interactions between neutrons and between protons is neglected, justified by the fact that there are four neutron-proton bonds for one neutron-neutron bond and one proton-proton bond. Even if it were possible to use the electromagnetic properties and spatial structure of the quarks in the nucleons, the calculations would be intractable. The nuclear geometric structure varying with the nuclides, the specific assumptions used are detailed in the paragraphs concerning 2H, 3H, 3He, 4He and the N > 2 isotopes. Judicious approximations are necessary to obtain an analytical formula for the binding energies.
3. Electric and Magnetic Coulomb Potential Energy
The Coulomb electric potential energy between two electric charges distant from r is  that can also be written as
that can also be written as 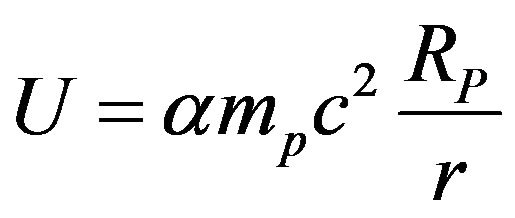 where
where 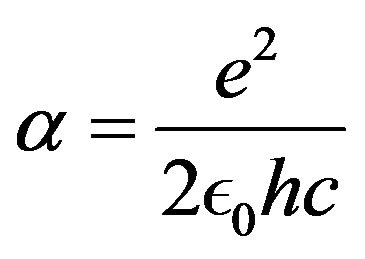 is the fine structure constant, mp the proton mass and RP the proton Compton radius.
is the fine structure constant, mp the proton mass and RP the proton Compton radius.
The Coulomb magnetic potential energy is repulsive when the magnetic moments between two magnets are collinear and opposite, as in the deuteron, thus giving a positive potential: . This formula can also be written as
. This formula can also be written as  where gi and gj are the nondimensional Landé factors. When the magnetic moments are not collinear, a coefficient Sij (see below the general formula) have to be used. It seems that it is the first time that the electric and magnetic Coulomb’s formulas are united in a single formula to describe static interactions between particles having both electric and magnetic properties [5,9,10,11].
where gi and gj are the nondimensional Landé factors. When the magnetic moments are not collinear, a coefficient Sij (see below the general formula) have to be used. It seems that it is the first time that the electric and magnetic Coulomb’s formulas are united in a single formula to describe static interactions between particles having both electric and magnetic properties [5,9,10,11].
The total electromagnetic potential energy Uem of a nucleus is the sum of the electrostatic interaction energy Ue between particles i and j with electric charges ei and ej and the magnetostatic interaction energy Um between their magnetic dipoles μi and μj. Formulas (1) and (2) show that the Coulomb potential is attractive or repulsive depending on the sign of the product of the electric charges:
 (1)
(1)
where
 (2)
(2)
is the tensor operator [12] and rij is the internucleon vector. Sij is positive for magnetic repulsion and negative for magnetic attraction, depending on the relative orientation and position of the magnetic moments of the nucleons. gi is the Landé factor of the ith nucleon. The electromagnetic nuclear potential is the product of αmpc2 = 6.8 MeV, almost equal to the α particle binding energy, and a purely numerical function to be determined (see Paragraph 11 for more details).
4. Deuteron Electromagnetic Binding Energy
The deuteron is the simplest nucleus beyond the protium, containing one proton with one positive charge +e and one neutron containing electric charges with no net charge. The electric field of the proton, acting on a neighboring neutron, separates the neutron charges, creating an induced dipole. The negative charge is attracted by the proton and the positive charge is repulsed at a greater distance from the proton than the negative charge. Therefore, according to Coulomb’s law, the attraction is larger than the repulsion, giving a net attraction (Figure 1). The positive charge of the neutron may thus be neglected in a first approximation, giving a simple equation for the electromagnetic potential, easily solvable to obtain the binding energy. As explained above, for the sake of simplicity, we shall consider, in this paper, only the negative charge of the neutron in the deuteron. The electromagnetic potential of the deuteron with one positive charge in the proton and one negative charge in the neutron, with collinear and opposite magnetic moments is, according to formulas (1) and (2):
 (3)
(3)
It is more complicated for the magnetic moments:
 (4)
(4)
The neutron-proton interaction potential energy is thus, numerically:
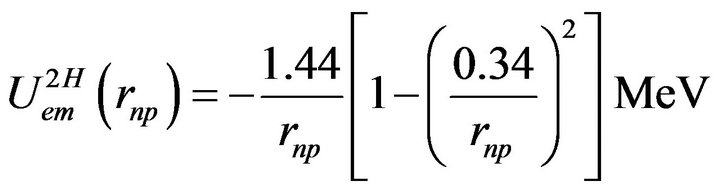 (5)
(5)
where rnp is in fm. The total binding energy is the total potential energy at its local minimum, according to the minimum potential energy principle. The derivative of the potential energy (3) relative to the radius rnp has to be a zero force at equilibrium:
 (6)
(6)
Solving this equation, one obtains the ratio :
 (7)
(7)
Replacing RP/rnp in the potential, the total binding energy writes:
 (8)
(8)
The binding energy per nucleon is, numerically:
 (9)
(9)
The calculated binding energy per nucleon of the deuteron, −0.8 MeV, is 30% weaker than the experimental value, −1.11 MeV. A better value (−1.1 MeV) is obtained when the positive charge is taken into account [8]. The binding energy of the deuteron is thus predicted electromagnetically although the precision is poor due to the neglect of the positive charge of the neutron but the advantage is to have an analytical formula. This calculation uses only classical electrostatics, magnetostatics and fundamental constants.
5. Triton Electromagnetic Binding Energy
The triton 3H (Figure 2), having only one proton, the proton-proton interaction is inexistent. The two neutrons are separated from the proton by rnp. The distance between the two neutrons being twice that between the proton and the neutrons, their electric and magnetic interactions may be neglected. The total electrostatic potential, due essentially to the two neutron-proton interaction, is given by formula (1):
 (10)
(10)

Figure 2. Approximate electromagnetic structure of the A = 3 nuclides. The electrostatic attraction between neutrons and protons is attractive as in the deuteron. The magnetic moments of the triton and the helion are approximately, respectively, equal to those of the proton and the neutron, as schematized on the picture but they have different orientation. The repulsion between the protons (or the neutrons) is smaller because they are farther away, explaining the binding energy per nucleon larger than that of the deuteron. The triton and the helion 3He and 3H being mirror nuclei, we need only to calculate the binding energy of the triton and then switch round the Landé factors.
The magnetic moment of the proton, being almost perpendicular to those of the two neutrons and to their common vector radius rnn, formula (2) becomes:
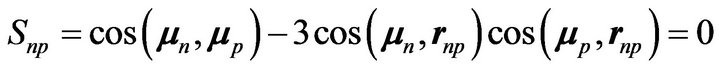 (11)
(11)
The magnetic interaction between the 2 neutrons cannot be neglected because it is the only repulsive force. According to formula (1) we have:
 (12)
(12)
The magnetic moments μn1 and μn2 of the neutrons being almost collinear and opposite, their magnetic interaction is repulsive:
 (13)
(13)
With Sn1n2 = 2 and 2 np bonds, the magnetic component of the potential between the neutrons distant by 2rnp is:
 (14)
(14)
Applying the general formula (2), the electromagnetic interaction potential in 3H is the sum of the electric attraction between the proton and the two neutrons equilibrated by the repulsion between the magnetic moments of the two neutrons as shown on Figure 2. Adding the electrostatic potential (10) and the neutron-neutron magnetic potential,  (14), the magnetic neutronproton potential being zero, equation (11), the electromagnetic potential of the 3H nucleus becomes:
(14), the magnetic neutronproton potential being zero, equation (11), the electromagnetic potential of the 3H nucleus becomes:
 (15)
(15)
The equilibrium distance is obtained by derivation, as for the deuteron:
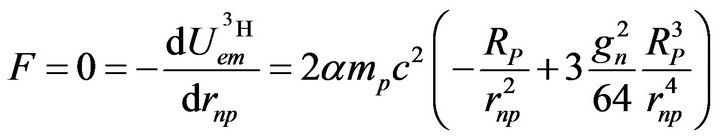 (16)
(16)
Solving the preceding equation, we have:
 (17)
(17)
Putting this value into the potential (15) gives the total binding energy of the triton:
 (18)
(18)
The binding energy per nucleon is thus −3.7 MeV for = −2.83 MeV experimental (30% error).
6. Helion Electromagnetic Binding Energy
The helion nucleus is a triton where neutrons and protons are interchanged. Therefore, to calculate the binding energy of the helion it needs only to switch round the Landé factors, as shown on Figure 2. The binding energy per nucleon of the helion is thus:
 (19)
(19)
1% weaker than the experimental value  = −2.57 MeV.
= −2.57 MeV.
7. α Particle Electromagnetic Binding Energy
It is well known that the magnetic moment of the α particle is zero. The simplest structure of the 4He nucleus being a tetrahedron, approximately regular, we shall assume that the magnetic moments are collinear and oriented oppositely along the neutron-neutron and the proton-proton vectors by reason of symmetry (Figure 3). Therefore the magnetic moments are inclined at 60˚ with respect to the neutron-proton edges and collinear with the proton-proton and neutron-neutron edges.
The helium 4He (Figure 3) has one nn, one pp and 4 np bonds. We may neglect, in a first approximation, the interactions between neutrons and between protons because there are four neutron-proton interactions for one neutron-neutron and one proton-proton interaction. Each proton inducing each neutron, the induced electric charge in one neutron is around twice that of the deuteron:

Figure 3. Tetrahedral 4He. The magnetic moment of the α particle being zero as it is well known, the magnetic moments of the nucleons are paired, collinear and oppositely oriented by reason of symmetry. Therefore, there is electric and magnetic repulsion between protons and between neutrons, neglected in a first approximation in comparison with the four neutron-proton bonds. The main magnetic interaction is the tensor repulsion between neutrons and protons whose projections on their common edge are oppositely oriented both outward (or both inward).
 (20)
(20)
As explained in the assumptions section, the magnetic moments of one proton and one neutron being perpendicular, the first term of Equation (2) is zero. Being inclined at 60˚ with respect to their rnp bond (Figure 3), their projections on their common edge have the same orientation and, thus, the same cosines because they are assumed to be both oriented outward (or inward). The projections on the edges of the tetrahedron rnp are opposite. Formula (2) becomes:
 (21)
(21)
The general formula (2) gives thus a factor Snp = 3/4 instead of 2 in the deuteron formula (5). The magnetic component of the 4He potential is thus 3/8 times that of the deuteron. According to formula (2), the magnetic component of the electromagnetic potential of the neutron-proton bond in 4He is thus:
 (22)
(22)
With 4 neutron-proton bonds, Equations (20) and (22), the total electromagnetic potential of the α particle, is:
 (23)
(23)
At equilibrium, the force, being zero, the potential is at its minimum, obtained by derivation:
 (24)
(24)
The ratio of the proton Compton radius over the distance between a proton and a neutron in a 4He nucleus is:
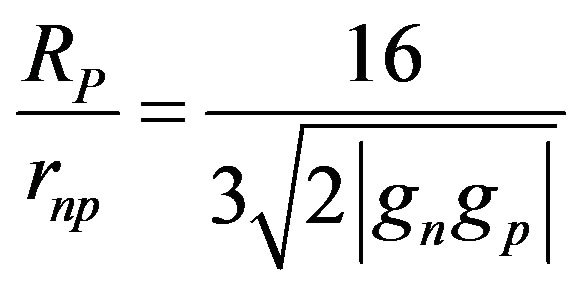 (25)
(25)
Replacing  at equilibrium in the potential gives the total binding energy of 4He:
at equilibrium in the potential gives the total binding energy of 4He:
 (26)
(26)
or, per nucleon:
 (27)
(27)
differing by 5% from the experimental value, −7.07 MeV.
8. Hydrogen and Helium Isotopes with N > 2
The 2H and 4He isotopes having halo neutrons, the excess neutrons (N > 2), are almost unbound, thus simplifying the calculations. Indeed, the total binding energy being almost constant, it suffices to divide it by the atomic number.
A preceding calculation on hydrogen isotopes [7] taking into account the interaction between neutrons has given coherent results. It has since been found that the H and He isotopes with N > 2 have almost the same total binding energy. This results in an important simplification for the hydrogen and helium isotopes with N > 2 whose binding energies are obtained by dividing the 3H or 4He total binding energy by their mass number (Figure 4).
9. Nuclear and Chemical Energies
The energy needed to separate an electron from a proton is given by the Rydberg constant, half the Hartree energy, according to the Bohr formula:
 (28)
(28)

Figure 4. Calculated and experimental binding energies per nucleon of the hydrogen and helium isotopes. 2H, 3H, 3He and 4He have been calculated individually. Nuclides with more than two neutrons have been calculated from the maximum binding energy by assuming a zero separation energy for the extra neutrons. Therefore B, for a given Z, is independent of the neutron number N > 2 and B/A decreases in proportion, thus unable to predict the peaks at even N on the experimental curves. The experimental and the theoretical isotopic curves coincide approximately. The binding energies, calculated from nuclear masses [13,14], are taken positive on the graph.
where me is the electron mass. The calculated separation energy of a neutron from a proton is the total binding energy of the deuteron [7]:
 (29)
(29)
 (30)
(30)
This calculated binding energy of the deuteron is 30% weaker than the experimental value, −2.2 MeV due to the approximations used. The order of magnitude of the nuclear/chemical energy ratio may thus be characterized by
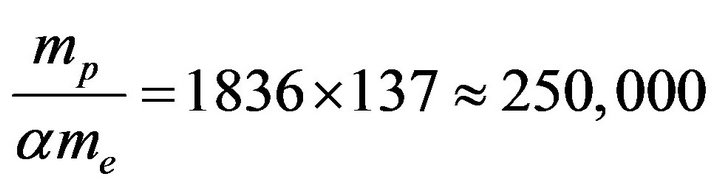 (31)
(31)
The experimental binding energies per nucleon vary from 0.6 MeV for 7H to almost 9 MeV for Fe. This gives a ratio varying from 44,000 to 662,000, coherent with the above calculated value and the usual estimation of one million for the nuclear/chemical energy ratio. The binding energy of any nuclide is given by ampc2 multiplied by a coefficient depending only on the electromagnetic structure of the nucleus. This is not numerology, it is the strict application of Coulomb’s laws.
10. Conclusions
All calculations of the binding energies of nuclei in the literature use fitting parameters, cutoff, corrections, estimations or ad hoc constants, unable to evaluate even the order of magnitude of the nuclear energy. The binding energy of the simplest nucleus beyond the proton, the deuteron, has never been calculated, only explained by saying that its size exceeds the range of the nuclear forces, thus rather weakly bound [12].
At the present time, only the electromagnetic approach is able to calculate nuclear binding energies. Figure 4 shows graphically and on Table 1, the results of the hydrogen and helium isotopes compared with the experimental values. In order to obtain analytical formulas, rough approximations are necessary. Thus the precision is between 1% and 30%, depending on the approximation used. The order of magnitude of the nuclear to chemical energy ratio has been obtained for the first time, using only fundamental constants, the fine structure constant combined with the masses of the proton and the electron.
• 11. Fundamental Constants Used [15]
• Light velocity:
 (32)
(32)
• Proton-electron mass ratio:
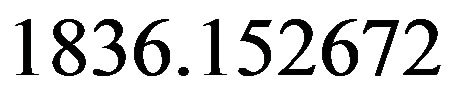 (33)
(33)
• Fine structure constant:
 (34)
(34)
• Proton mass:

Table 1. Binding energies per nucleon of 2H, 3H, 3He and 4He. The formulas are derived in the text of the paper. Discrepancies appear between calculated binding energies, due to the approximations used, with or without the positive charge of the neutron. 3H and 3He differ only by their Landé g factor, explaining why 3H has a greater binding energy than 3He. The ratio between the binding energies of the deuteron and the α particle is found to be between 6 and 8, for 6.5 experimental.
 (35)
(35)
• Proton Compton radius:
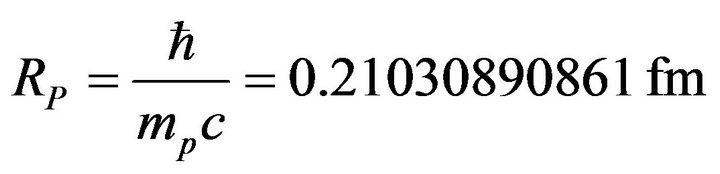 (36)
(36)
• Nuclear magneton:
 (37)
(37)
• Magnetic moments of the neutron and the proton: μn and μp and their corresponding Landé factors,
 (38)
(38)
where i means n or p.
• Relation between vacuum dielectric permittivity and magnetic permeability:
 (39)
(39)
• Nuclear electrostatic energy constant:
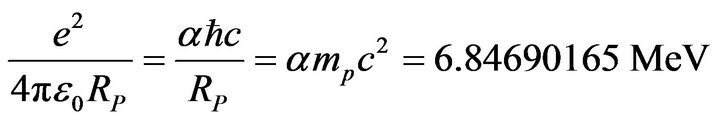 (40)
(40)
This fundamental constant, 4% weaker than the α particle binding energy per nucleon (−7.07 MeV), is the nuclear equivalent of the Hartree energy or twice the hydrogen atom binding energy (Rydberg constant).
• Nuclear magnetic energy constant:
 (41)
(41)