A Fractal Menger Sponge Space-Time Proposal to Reconcile Measurements and Theoretical Predictions of Cosmic Dark Energy ()
1. Introduction
The discrepancy between theoretical prediction and cosmological measurements of the entire energy content of our universe [1-3] is resolved in the present work. This is achieved by combining classical Newtonian mechanics with a novel fractal interpretation of our familiar classical space. We start by assuming that space itself is a Cantorian set-like fractal akin to a Menger sponge [4,5]. This immediately leads us to qualitative and equally important, if not more important, quantitative results [6]. From the topology and geometry of the Menger sponge [4,5,7] and the classical expression for kinetic energy we can draw the inference that only 4.5% of the entire energy of the cosmos is ordinary matter and energy [1,3,6]. The rest of what Einstein’s equation predicted, namely 100% − 4.5% = 95.5% is actually due to the zero fractal volume of the Menger sponge-like “non-space” (see Figures 1 and 2) which exists indirectly by not being there or being there only in the Aristotelian sense of Potentia not unlike many other things in quantum mechanics such as the well documented Bohm-Aharonov effect [4-6]. The matter and energy corresponding to this space structure with a relatively large Hausdorff dimension but a zero classical 3D volume, if they can be called matter and energy in the ordinary sense at all, are for the time being and the foreseeable future completely inaccessible to us [1-3]. The situation is not dissimilar to the zero and empty set of transfinite set theory because zero and negative Menger-Urysohn dimensions [6,7], although referring to zero and empty sets, are still indispensible to a logical, coherent, complete and consistent set theory and
thus mathematics and consequently physics [7,8].
The present analysis starts by showing that Einstein’s  [9,10] must be revised to
[9,10] must be revised to  and conclude that
and conclude that
 (1)
(1)
in complete agreement with the WMAP and supernova measurements [1-3]. This means that only 4.5% of the expected energy exists while the rest of 95.5% must be assumed to be missing and is therefore referred to as “dark” or missing energy [1-3,6]. Subsequently the analysis is refined and extended to find the exact  which turned out to be 1/22.18033989 being the ratio of
which turned out to be 1/22.18033989 being the ratio of

Figure 2. The entire cosmos as a cotton candy. This would be a possibility for explaining how such a huge form is only 4.5% of what it seems to be.
 and
and  where
where
 . Consequently the exact
. Consequently the exact  is given by
is given by
 (2)
(2)
It should be noted that  is the well known Hardy’s probability of quantum entanglement [11]. This fact reveals the quantum roots of our classical theory and we note on passing that dark energy is the absolute value of the negative energy of the quantum Schrödinger wave while the positive ordinary energy is that of the quantum particle, a subject which will not be discussed within the present work but is explained in some detail in Overview Charts No. 1-3 as well as Figures 3 and 4 [8,11].
is the well known Hardy’s probability of quantum entanglement [11]. This fact reveals the quantum roots of our classical theory and we note on passing that dark energy is the absolute value of the negative energy of the quantum Schrödinger wave while the positive ordinary energy is that of the quantum particle, a subject which will not be discussed within the present work but is explained in some detail in Overview Charts No. 1-3 as well as Figures 3 and 4 [8,11].
2. Analysis
2.1. Classical Analysis Using the Menger Sponge
A Menger sponge is basically a three dimensional fractal [4,5,7] constructed by drilling infinitely many cubic holes into it iteratively, the result of which is shown in Figure 1(c). A discussion of this well known fractal with numerous applications in physics, chemistry and biology may be found in many of the excellent text books on the subject [4,5,7]. Assuming empty space itself and not

Figure 3. A naive geometrical interpretation of geometrical density or Hausdorff measure  which decides upon the magnitude of dark energy density of the quantum wave
which decides upon the magnitude of dark energy density of the quantum wave .
.
merely matter to be a Menger sponge fractal, then the Hausdorff dimension of this space could be set equal to the Menger sponge (see Figure 1(a)):
 (3)
(3)
Let us now ponder carefully what DH (M) really measures and refers to. Since the original cube was obviously 3 dimensions and we have at least in theory removed almost the entire substance, i.e. space which makes it upthen it follows that the large dimension of  refers basically the quasi-Hausdorff value to the space removed rather than the sparse Cantor point set left. Said in a different way the volume of the Menger sponge space is now zero and nothing is left except a zero measure infinitely long and infinitely thin fractal line in three dimensional classical spaces. What could be said to have remained from this 3D space is a zero volume Menger fractal of a Hausdorff dimension equal to that of the complement space of the Menger sponge and given by (see Figure 1(b))
refers basically the quasi-Hausdorff value to the space removed rather than the sparse Cantor point set left. Said in a different way the volume of the Menger sponge space is now zero and nothing is left except a zero measure infinitely long and infinitely thin fractal line in three dimensional classical spaces. What could be said to have remained from this 3D space is a zero volume Menger fractal of a Hausdorff dimension equal to that of the complement space of the Menger sponge and given by (see Figure 1(b))
 (4)
(4)

Figure 4. A naive geometrical interpretation of  of the ordinary energy density of the quantum particle
of the ordinary energy density of the quantum particle .
.
It is important to realize that the relative ratio of what is left of real space to the original 3D cube is obviously the difference between 3D “solid” and “smooth” Euclidean space and a cotton candy-like (see Figure 2) Menger sponge dimension divided by 3D. In other words our space “density” ratio is
 (5)
(5)
It is thus imperative to understand that this  must be included in the classical kinetic energy expression of Newton which presupposes a “smooth” “solid” nonfractal space. Consequently
must be included in the classical kinetic energy expression of Newton which presupposes a “smooth” “solid” nonfractal space. Consequently

must be logically extended to

and therefore

That means
 (6)
(6)
This is only 4.5% from what the relativistic nonquantum equation of Einstein predicts. However it is clear from the full agreement of the energy predicted by EQR with the accurate experimental measurement of WMAP and others [1-3] that  does not apply to extreme situations like when considering the cosmos as a whole.
does not apply to extreme situations like when considering the cosmos as a whole.
In the next section we will give some deeper and mathematically more sophisticated reasons why EQR is the correct equation for calculating the energy of the cosmos and that  could be seen as resulting from accounting for a fundamental quantum mechanical effect, namely quantum entanglement [8,11].
could be seen as resulting from accounting for a fundamental quantum mechanical effect, namely quantum entanglement [8,11].
2.2. Quantum Relativity Analysis
It is well known that Hardy’s quantum probability [8,11] is generic and is given by

where  [8,11]. At least in theory the two particles
[8,11]. At least in theory the two particles  which were tested to very high accuracy experimentally lead to the conclusion that for a single particle we would have
which were tested to very high accuracy experimentally lead to the conclusion that for a single particle we would have
 .
.
Now Einstein’s equation is a one particle equation
 .
.
Intersecting this relativistic formula with the quantum formula, a quantum relativistic energy formula is easily found to be (see Figures 5 and 6)
 (7)
(7)
This is almost the same result obtained earlier on using classical mechanics and the Menger sponge space in the previous Section 2.1.
2.3. Analysis Using K3 Kähler Manifold
The Kähler manifolds are used for compactification in superstrings and related theories [8]. Let us assume that

Figure 5. Quantum relativity theory as an intersection of the three major fundamental theories of physics.

Figure 6. The effective quantum gravity energy formula  as a synthesis of Newton, Einstein and quantum theories.
as a synthesis of Newton, Einstein and quantum theories.
space and time are fused together and modeled by such a Kähler manifold. The Betti number b2 for K3 is given by [12,13]
 (8)
(8)
This number could be thought of as counting the number of 3D holes in K3. Thus compared with Einstein’s 4D smooth manifold for which b2 = 1, our K3 has 22 times more 3D holes in it [12,13]. Thus we could write the ratio  as [12,13]
as [12,13]
 . (9)
. (9)
This is obviously a very useful scaling exponent and we see that  and consequently multiplied with
and consequently multiplied with  of Einstein we find again our EQR energy formula
of Einstein we find again our EQR energy formula
 (10)
(10)
Thinking deeply about this result one may be yet again surprised to realize that in retrospect, it should have been expected for the following obvious reason. The difference between Newton’s kinetic energy formula
 and Einstein’s maximal energy
and Einstein’s maximal energy  is formally a factor half and setting v = c. Subsequently we showed that
is formally a factor half and setting v = c. Subsequently we showed that  by assuming a different Menger fractal geometry instead of the smooth geometry of Newton’s space. Here again EQR kept the same form of Newton and Einstein and everything else was taken care of by a simple factor 1/22. Then in our second derivation the same result was found after fusing quantum entanglement with special relativity. Again if we remember that gauge theory started with the idea of Weyl scaling and that Nottale’s high energy particle physics and cosmology theory is based on scale relativity principle, then we realize that this was also to be expected in our case. For these reasons the ratio of the homology of a classical geometry such as b2 = 1 of Einstein’s space and the b2 = 22 of a complex manifold like our K3 used here [12,13] harbors more than meets the eyes in the harmless appearance of a simple scaling factor.
by assuming a different Menger fractal geometry instead of the smooth geometry of Newton’s space. Here again EQR kept the same form of Newton and Einstein and everything else was taken care of by a simple factor 1/22. Then in our second derivation the same result was found after fusing quantum entanglement with special relativity. Again if we remember that gauge theory started with the idea of Weyl scaling and that Nottale’s high energy particle physics and cosmology theory is based on scale relativity principle, then we realize that this was also to be expected in our case. For these reasons the ratio of the homology of a classical geometry such as b2 = 1 of Einstein’s space and the b2 = 22 of a complex manifold like our K3 used here [12,13] harbors more than meets the eyes in the harmless appearance of a simple scaling factor.
2.4. The Lorentz-Like Transformation Leading to Quantum Relativity
To connect all the preceding three different derivations with the original theory of Lorentz and Einstein, it is instructive to see that a similar derivation in the spirit of Lorentz-Einstein transformation holds and leads to the same result of quantum relativity . Accepting the three fundamental phenomenological effects of special relativity, the following transformations are evidently consistent, i.e. [7]
. Accepting the three fundamental phenomenological effects of special relativity, the following transformations are evidently consistent, i.e. [7]
 (11)
(11)
where  is a boost which does not need to be defined by anything related directly to v/c where c is the phenomenologically and experimentally accepted constant speed of light. Inserting in Newton’s kinetic energy we find
is a boost which does not need to be defined by anything related directly to v/c where c is the phenomenologically and experimentally accepted constant speed of light. Inserting in Newton’s kinetic energy we find
 (12)
(12)
On the other hand we could use the conventional Lorentz transformation in the unconventional form of light cone velocity used in superstrings quantization [14,15] and extend it to encompass a light cone mass as follows:
 . (13)
. (13)
Inserting again the Newton kinetic energy we find
 . (14)
. (14)
Setting v = c, c = m = 1 and equating E1 and E2 one finds
 (15)
(15)
This leads to a quadratic equation in  with the only positive root
with the only positive root  [16]. Inserting in E1 one finds immediately that
[16]. Inserting in E1 one finds immediately that
 (16)
(16)
which confirms without any doubt the correctness of all the previous three derivations of Sections 2.1, 2.2 and 2.3 of the present work. In Chart Nos. 4 and 5 we give an overview comparing different Lorentz-like transformations leading to the same robust result .
.
3. Negative Gravity as Compactified Dimensions
When an elastic surface is acted upon with a load, it curves [17,18]. The theory of such elastic surfaces is highly developed in a remarkably successful theory called theory of elasticity [17-20]. This theory and its sister, theory of plasticity, is the basis of all structural engineering science which gave us shell structures [17-19] covering large sports and airport halls without supporting columns and thin fuselages which carry passengers across the Atlantic in a few hours. When such an elastic or elasto-plastic surface is sufficiently thick, long and narrow then an interesting curvature phenomena takes place called anticlastic curvature [20]. The point is that when the long thick elastic structure is bent, then its cross section curves in the opposite direction. This classical analogy is helpful to visualize the effect of the compactified 22 dimensions belonging to the 26 dimensions of say the heterotic superstring theory or the old bosonic string theory of Veneziano and Nambu [14]. Thus we are suggesting here that 26 − 4 = 22 compactified dimensions are a string analogy to the anticlastic curvature observed in thick elastic structural beams as well as long, thin walled elastic tubes subjected to local singular loads somewhere in the middle of the length direction [18]. In turn this anticlastic curvature and the corresponding compactified 22 dimensions produce the effect of negative gravity which can explain the observed increased acceleration in the expansion of the universe [1-3,6]. Figure 7 and Chart No. 6 may help in understanding the basic idea behind negative gravity. Thus we advocate that the 22 compactified, curled extra dimensions are not only the cause of dark energy, but that they also play the role of Einstein’s cosmological constant or negative gravity. Similar qualitative conclusions may be drawn using the theory of polar media due to the brothers

Figure 7. Here D(4) = 4 is the dimension of Einstein’s spacetime, R(4) = 20 are the number of independent components of Riemann curvature tensor in dour dimensions and R(4) = 256 are the number of all the components of the same curvature tensor, v is the velocity and c is the speed of light.
Cosserat [19] and also using Cartan’s torsional curvature [9,10,17].
4. The Role of Transfinite and Hyperbolic Geometry
The thread connecting the different themes of all the preceding sections is the profound impact of non-classical and hyperbolic geometry on physics. In this section we stress this point by referring to the explicit impact of non-classical geometry and its Lie symmetry groups as presented in overview Chart 7 on physics [12-16].
5. Conclusions
Assuming that space-time is akin to a Menger sponge fractal we were able to show that a purely classical energy expression  changes to
changes to

The result of this Newtonian non-relativistic and nonquantum derivation is confirmed using a variety of sophisticated mathematical methods including a Lorentzlike transformation as well as an intersection between Hardy’s quantum entanglement

and Einstein’s maximal energy . Thus
. Thus
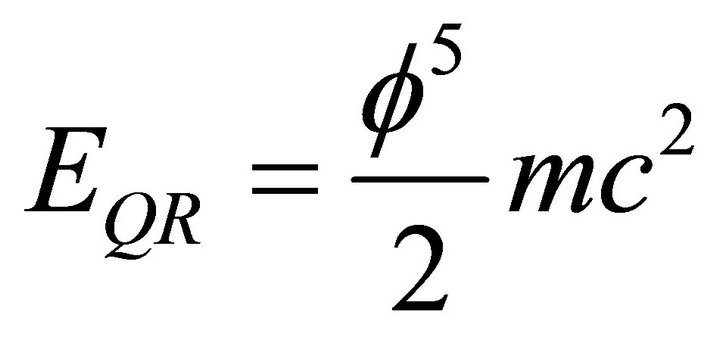 may be regarded as a quantum relativity formula and therefore
may be regarded as a quantum relativity formula and therefore  may be viewed in various ways as:
may be viewed in various ways as:
1) A Weyl-Nottale scaling expression for quantum relativity [6].
2) A measure for the hypothetical dark energy of the cosmos

in full agreement with measurements [1-3,6].
2) The magnitude of quantum entanglement involved in quantum relativity at the Hubble radius scale of the universe [6].
3) A measure for the negative gravity or anticlastic curvature effect responsible for the increasing rate of expansion of the universe.
4) The ratio of two Betti numbers characterizing the homology of Einstein’s space and a K3 Kähler space namely  [12,13].
[12,13].
It is important to note that recent investigation by the present author has revealed that  is the energy of the quantum particle while
is the energy of the quantum particle while  is the dark energy of the quantum wave. The sum is Einstein’s energy
is the dark energy of the quantum wave. The sum is Einstein’s energy . Thus Einstein’s formula is blind to any distinction between ordinary energy and dark energy. (See also Overview Charts 1-3 and Figures 6 and 7).
. Thus Einstein’s formula is blind to any distinction between ordinary energy and dark energy. (See also Overview Charts 1-3 and Figures 6 and 7).
Overview Chart

Chart No. 1. The Kaluza-Klein energy of the quantum particle and the dark energy of the quantum wave.

Chart No. 2. Einstein energy as the sum of the ordinary energy of the zero set particle and the dark energy of the empty set wave in five dimensions.

Chart No. 3. The energy corresponding to the wave-particle duality and the corresponding empty set-zero set duality in D = 5 Kaluza-Klein spacetime.

Chart No. 4. Flow chart for probabilistic strategy to derive E-quantum relativity using Hardy’s quantum entanglement probability method for .
.

Chart No. 5. Flow chart for the on light cone strategy to derive E-quantum relativity as in the light cone quantization of super string theory.


Chart No. 6. The dark energy of the quantum wave as deduced from the ordinary energy of the quantum particle using general relativity and Heterotic superstrings.

Chart No. 7. Geometrical interpretation of the ordinary energy of a quantum particle and the existence of minimal areas.