Elasticity Mapping Analysis of Apical Cell Periphery Actin Structures of Normal Fibroblasts and Cervical Cancer Cells ()
1. Introduction
The mechanical features of cells are unique indicators for cellular states and diseases. In mesenchymal stem cells, these features are attributed to their diverse characteristics and states [1,2]. Malignant cancer cells exhibit lower stiffness than the corresponding normal cells [3,4]. Thus, it is hoped that the cell mechanical features play significant roles in cell diagnosis and analysis.
There are several methods to measure the mechanical features of cells including micropipette aspiration [5], optical stretcher [6], and atomic force microscopy (AFM) [7]. These technologies measure the surface tension, stiffness, or deformation of cells wholly or locally in physiological conditions. The micropipette aspiration elucidates cell surface tension partially. The optical stretcher elucidates whole cell deformation and AFM measures the cell stiffness or viscoelasticity locally. Especially the spatial resolution of AFM measurements for cell mechanical features is outstanding compared to other methods [8-10]. AFM can investigate the mechanical properties of cell surface with high-sensitivity (~1 pN) and -spatial resolution (~1 nm) under physiological cell culture conditions based on the employed cantilever.
The mechanical features are largely attributable to the actin cytoskeleton [11-14]. Stress fibers are specific determinants of cell mechanics [15], and cortical actin has also been reported to promote cortical rigidity [16,17]. Dominant actin substructures differ by cell type as well as their subcellular localization. Thus, by analyzing the mechanical features of cells, it is possible to shed light on the characteristics of their intricate actin networks. Highly sensitive and spatially resolved AFM measurements are promising analytical methods for investigation of biological surfaces. The cortical rigidity of mitotic round cells is less than that of trypsinized round cells despite of similar cell morphology and optical-microscopy visible actin networks [18]. It is also known that the stiffness of the cleavage furrow region of cells in cytokinesis, which contains an actomyosin contractile ring, drastically increases [10].
The mechanical features are cell-type specific. Cancer and normal cells exhibit different mechanical features because of the difference of their optical-microscopy defined actin cytoskeleton structures [4,19]. Our previous study showed that the regulatory mechanisms for actin cytoskeleton structures are different in normal stromal and cancer cells [20]. We demonstrated that the mechanical responsiveness to actin-modifying agents was different between these cells. In particular, the mechanical responsiveness of cancer cells was relatively affected by calyculin A treatment but hardly affected in normal stromal cells. Calyculin A is a myosin light chain phosphatase inhibitor that activates actomyosin formation and enhances actin polymerization (Figure 1) [21]. Additionally, the cortical rigidity of Drosophila embryonic S2R+ cells was increased via accelerating cortical actin formation by calyculin A treatment [17]. However, it is unclear why and how actin cytoskeleton structures generate these variations. Because surface stiffness measurement by AFM is a highly sensitive method which can detect optical-microscopy invisible information about the maturation or strength of the actin cytoskeleton network near cell surface [18,20], in this study to clarify the actin cytoskeleton structures responsible for these variations in each cell type, we examined the surface mechanical structures of normal fibroblasts and cancer cells using local elasticity mapping method of AFM.
2. Materials and Methods
2.1. Materials
The pyramidal probe (SN-AF01S-NT; spring constant: 0.09 N/m) was purchased from Seiko Instruments Inc. (Tokyo, Japan). Human fetal lung normal fibroblast TIG-1 cells [22] and human cervical cancer Hela cells were obtained from Health Science Research Resources Bank (Osaka, Japan). Antibiotics were purchased from Sigma-Aldrich (St. Louis, MO). pEGFP-actin vector was purchased from Clontech (Mountain View, CA). Other reagents were purchased from Sigma-Aldrich, Wako Pure Chemical Industries Ltd. (Osaka, Japan), or Life Technologies Japan Ltd. (Tokyo, Japan).
2.2. Cell Culture
TIG-1 and Hela cells were maintained in DMEM containing 10% FBS and antibiotics (100 units/mL penicillin G, 100 μg/mL streptomycin sulfate, and 0.25 μg/mL amphotericin B). The culture medium was replaced three times a week. Cells adhered to the culture dishes were manipulated by AFM.
2.3. Transfection and Fluorescence Observation
TIG-1 and Hela cells were transfected with pEGFP-actin
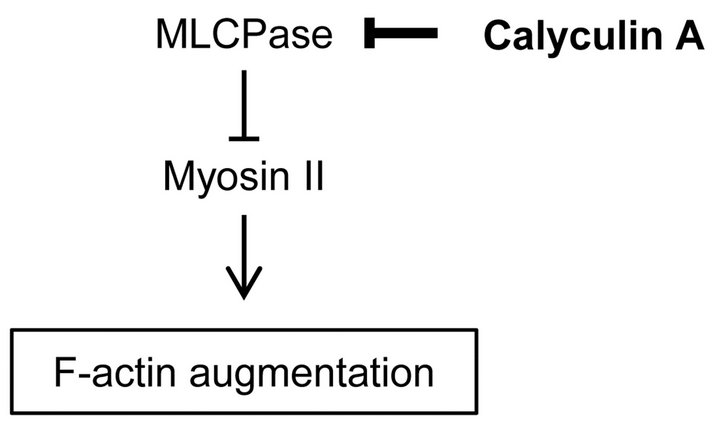
Figure 1. Regulation pathway of actin filaments formation by calyculin A.
vector by electroporation (ECM399; BTX, Holliston, MA), as recommended by the manufacturer. The transfected cells were observed by confocal laser scanning microscopy (CLSM) (FV-1000; Olympus, Tokyo, Japan) using a 60× oil immersion lens (NA = 1.42). The images were obtained from the upper part of the cell at intervals of 30 sec after treatment with 0.1 nM of calyculin A.
2.4. AFM Measurements
TIG-1 and Hela cells were manipulated by AFM (Nanowizard 3; JPK Instruments AG, Berlin, Germany) at 37˚C. Combining the optical microscope (IX-71; Olympus) with AFM allows the probe to be placed on a particular region of the cell surface. In this study, the scanning area of the cell surface was set at 5.0 × 5.0 μm on the nuclear region. The scanning area was set to a grid of 128 pixels × 128 lines with a loading force of up to 0.5 nN at 93.75 μm/s. The cells were continuously scanned after calyculin A treatment. Each scanning round took about 12 min. The Young’s modulus of each pixel was calculated using the Hertz model [23]. Each force-distance curve was fitted using JPK data processing software (JPK instruments AG) as
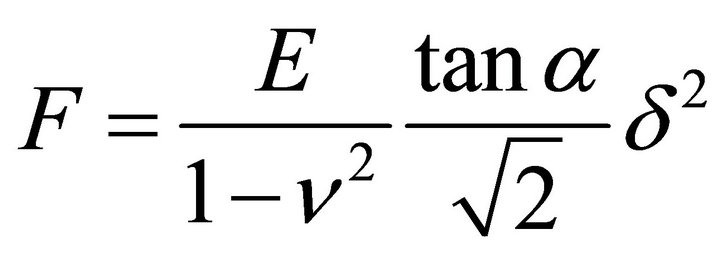 , (1)
, (1)
where F = force, δ = depth of the probe indentation, ν = Poisson’s ratio (0.5), α = half-angle to the face of the pyramidal probe (20˚), and E = Young’s modulus. More than 5 cells were used per experiment. The distribution of the Young’s modulus of each point was indicated with log scale [2,24].
3. Results and Discussion
3.1. Optical Microscopy Analysis of Actin Cytoskeleton of Cells Treated with Calyculin A
In this study, we used 2 types of cells: human TIG-1 fibroblasts and human cancer Hela cells. We previously demonstrated that the distribution of Young’s modulus and the mechanical responsiveness to calyculin A of these cells were different [20]. The Young’s modulus of TIG-1 cells slightly increased by calyculin A treatment, whereas that of Hela cells increased.
Firstly, we characterized these alterations by observing the reaction of the actin cytoskeleton of these cells to calyculin A. The cells were transfected with pEGFPactin vector by electroporation to force the EGFP-actin expression. In TIG-1 cells, EGFP-actin clearly localized in stress fibers, but in case of Hela cells distributed in cytoplasm (Figure 2). Then we time-lapse observed the alterations of apical actin structures in these cells during calyculin A treatment. Although it appeared that apical stress fibers of TIG-1 cells decreased a bit, calyculin A treatment did not cause any alterations in the actin cytoskeleton of these cells (Figure 2). Thus, it was difficult to define an alteration of actin cytoskeleton structures of these cells by optical microscopy.
3.2. Details of Mechanical Structures of TIG-1 and Hela Cells
We then determined the surface mechanical structures of these cells by the elasticity mapping method of AFM. The elasticity mapping method enables the visualization of those cell-periphery mechanical structures which are invisible by optical microscopy. In this study, in order to define the details of the mechanical structures of cell surface, we scanned a grid of 5.0 × 5.0 μm consisting of 128 pixels × 128 lines and scan resolution of 39.4 nm on the nuclear region of cell surface.
Figure 3(a) shows the sub-surface elasticity mapping images of TIG-1 and Hela cells. TIG-1 cell had many aligned stiff (>60 kPa) filamentous structures. On the other hand, Hela cell had some crooked filamentous structures whose stiffness was less than 10 kPa. The histogram of these elasticity data (Young’s modulus, E) are shown in Figure 3(b). The Young’s modulus was broadly distributed and followed a log-normal pattern as reported