Survival Probability of the Quantum Walk with Phase Parameters on the Two-Dimensional Trapped Lattice ()
1. Introduction
In recent years, the quantum walk on the trapped lattice has been intensively investigated due to importance applications in quantum information and computing. Therefore, many theoretical and experimental studies have been carried out to understand the effect of the trapping states on the quantum walk. For example, Agliari [1] considered a continuous-time quantum walk propagating on Erdos-Renyi random graphs in the presence of a random distribution of traps, and showed that the survival probability exhibits an exponential character which fluctuates depending on the trap concentration. Zahringer et al. [2] implemented a quantum walk using trapped ions. They used an experimental technique to determine the probability distribution along a line in phase space. It is shown that instabilities in the trapping frequency leads to decoherence and by change in the coupling strength due to high phonon numbers. Schimitz et al. [3] implemented the proof of principle for the quantum walk of one ion in a linear ion trap. It is shown that quantum interference enforces asymmetric, nonclassical distributions in the highly entangled degrees of freedom (of coin and position states). Xue et al. [4] implemented a multi-step quantum walk for a single trapped ion with interpolation between quantum and random walk by randomizing the generalized Hadamard coin flip phase. It is shown that the distribution of the walker spreads over unbounded position space rather than being folded back on itself. Agliari et al. [5] studied the continuous time quantum walk focusing on trapping processes on a ring and show that when the traps are arranged periodically the survival probability decays asymptotically, when the traps are arranged to form a cluster the survival probability decays exponentially, on the other hand for randomly distributed traps the survival probability decays algebraically. Eckert et al. [6] implemented the quantum walk with a neutral atom trapped in a ground state of optical potentials by using the concept of spatially delocalized quibits, that is, a coin defined through the presence of the atom in one out of two trapping potentials. It is shown that the shaking of the trap position on the quantum walk leads to a flat distribution in the transition from quantum to classical in the intermediate. Wojcik et al. [7] studied changing a phase at a single point in a discrete quantum walk. For certain values of this phase change and the internal coin-state of the walker it is shown the distribution exhibits the localization phenomenon. Altmann et al. [8] studied chaotic scattering, it is shown that noise enhances the trapping of trajectories in scattering systems. In particular, they show that weak noise leads to a slower decay of the survival probability. Karksi et al. [9] implemented a quantum walk on the line with single neutral atoms by deterministically delocalizing them over the sites of a one-dimensional spin-dependent optical lattice. For symmetric and asymmetric quantum walks, it is shown that the distribution is double peaked with large amplitude close to the edges of the distribution. Xu [10] studied coherent exciton dynamics modeled by continuous-time quantum walks on long-time range interacting cycles in which the distribution is shown to display a power law. Muelken et al. [11] in their quest for signatures of coherent transport studied exciton trapping in the continuous-time quantum walk, and show that the survival probability displays different decay domains. Finally, Gonulol et al. [12,13] shown that the time dependence of the survival probability of quantum walkers has a piecewise stretched exponential character depending on the density of traps.
It can be seen from the brief review that, in these studies, the focus is on how the traps affect the distribution of the survival probability of the usual quantum walk governed by Hadamard, Grover or Fourier coin operators. Recently, the quantum walk with phase parameters has been considered by a number of authors, see [14] for example. In this study, they proposed a different coin operator with parameters that alters the phase of the states of the walk on the line, and they show that the parameters in the coin operators affects the resulting probability distribution of quantum walk. The variance and shape of the probability distribution of states of the quantum walk depending on the phase parameters may be valuable results in point of view of the theory of quantum computation. Therefore in this paper we will study the survival probability of quantum walk with phase parameters on the two dimensional trapped lattice. To this end, we consider usual quantum walk with a special parametrization of the Fibonacci coin operator  [15] and define the coin operator as
[15] and define the coin operator as  where
where  is a two-dimensional generalizetion of the Fibonacci operator of
is a two-dimensional generalizetion of the Fibonacci operator of  and
and  is the diagonal phase adjustment. We show that the survival probability of the quantum walk with phase parameters on the trapped two dimensional lattice decays with time as the stretched exponentially for different initial states of walkers. We have also shown that stretched exponential decay parameter β of the walk can be arranged by phase parameter combination.
is the diagonal phase adjustment. We show that the survival probability of the quantum walk with phase parameters on the trapped two dimensional lattice decays with time as the stretched exponentially for different initial states of walkers. We have also shown that stretched exponential decay parameter β of the walk can be arranged by phase parameter combination.
This paper is organized as follows. In Section 2, we define the quantum walk on the square lattice with phase parameters. We also present in this section the time evolution for a single-particle walk as well as multi-particle walk in which the particles are distinguishable. In Section 3, we derive the survival probability using the exact numeration method of [18]. To account for randomization, we also calculate the mean survival probability in this section. In Section 4 the numerical analysis of the survival probability to determine how the traps affect its distribution is given. Section 5 is devoted to the conclusions.
2. The Quantum Walk with Phase Parameters on the Square Lattice
We consider the discrete-time quantum walk on the square lattice with boundary conditions. The coin space of a single walker is given by  where
where  corresponds to the chirality states left, right, up, and down respectively. In this paper we will put,
corresponds to the chirality states left, right, up, and down respectively. In this paper we will put,
 (1)
(1)
The position space is given by . The Hilbert space of the total system is given by
. The Hilbert space of the total system is given by . Recall that the evolution of the walk is given by
. Recall that the evolution of the walk is given by , where
, where  is the shift operator,
is the shift operator, 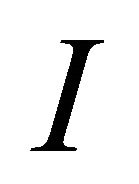 is the identity operator and
is the identity operator and  is the coin operator governing the walk. In this paper we will take
is the coin operator governing the walk. In this paper we will take , where
, where  is a two-dimensional generalization of the Fibonacci operator and
is a two-dimensional generalization of the Fibonacci operator and 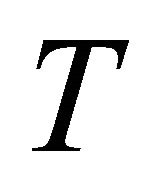 is the diagonal phase adjustment. In particular, diagonal phase adjustment can be defined as
is the diagonal phase adjustment. In particular, diagonal phase adjustment can be defined as , where
, where ;
;
 (2)
(2)
Denote the total number of sites on the lattice by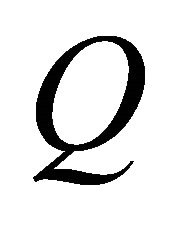 , then the shift operator is given by,
, then the shift operator is given by,
 (3)
(3)
We shall write the wave function of the walker at time  as,
as,
 (4)
(4)
with . We define the state of the particle by,
. We define the state of the particle by,
 (5)
(5)
where  for
for  represent probability amplitudes of the particle at site
represent probability amplitudes of the particle at site  at time
at time , depending on the chirality state of the particle. In terms of the initial state
, depending on the chirality state of the particle. In terms of the initial state , the evolution of the walk is given by
, the evolution of the walk is given by . The density operator of the quantum walk is given by
. The density operator of the quantum walk is given by . In terms of the density operator we can write the probability distribution of the walker at time
. In terms of the density operator we can write the probability distribution of the walker at time  as,
as,
 (6)
(6)
We should note that  can be written as,
can be written as,
 (7)
(7)
which is standard in papers on the quantum walk instead of the representation above involving the density operator.
On the other hand, single particle quantum walks can be easily generalized multi-particle quantum walks if the particles are assumed as uncorrelated, non-interacting and distinguishable. The multi-particle walk has been investigated by the author of the present paper [16,17]. The case where indistinguishability plays a role has also been considered. For simplicity in this study we consider walkers which are non-interacting distinguishable particles and they are initially uncorrelated. If we assume the 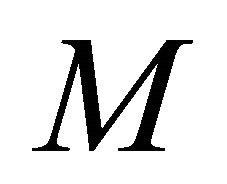 particles are distinguishable and are initially uncorrelated the Hilbert space is given by
particles are distinguishable and are initially uncorrelated the Hilbert space is given by
 (8)
(8)
or
 (9)
(9)
where  is the Hilbert space of the
is the Hilbert space of the  walker for
walker for . The evolution of the
. The evolution of the  -particle walk in which indistinguishability does not play a role is given by
-particle walk in which indistinguishability does not play a role is given by , where
, where  is the same for each walker. The initial state of the
is the same for each walker. The initial state of the  particles is written as
particles is written as
 (10)
(10)
Alternatively, Equation (10) is given by a tensor product of the single walker initial states as
 (11)
(11)
where  for
for  is the
is the  particle state with chirality
particle state with chirality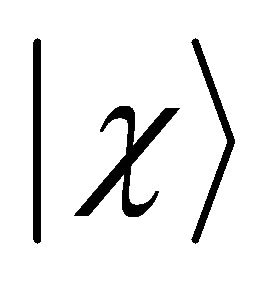 , and position
, and position  (recall we are assuming that there are
(recall we are assuming that there are  sites on the square lattice). In terms of
sites on the square lattice). In terms of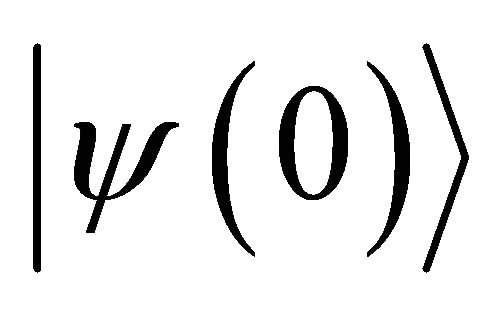 , the evolution of the walk is given by
, the evolution of the walk is given by . Using the reduced density operator
. Using the reduced density operator  we can write the probability distribution of a single walker at time
we can write the probability distribution of a single walker at time  by
by
 (12)
(12)
where .
.  in Equation (12) represents the probability of a single walker at site
in Equation (12) represents the probability of a single walker at site 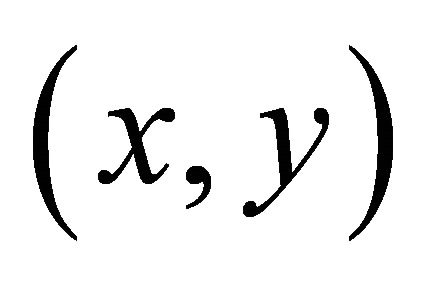 at time
at time  when the walker starts from site
when the walker starts from site 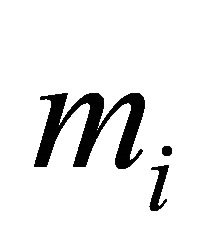 at
at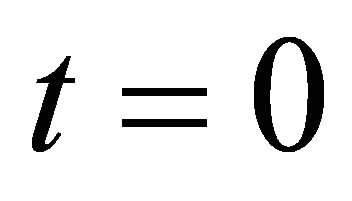 . The set
. The set  is the set of transition probabilities from
is the set of transition probabilities from  to
to  of a single particle, which is the same interpretation given by Equation (6).
of a single particle, which is the same interpretation given by Equation (6).
3. Survival Probability
In [18] the exact numeration method was used to calculate the survival probability in the classical random walk. This method was used by the authors in [12] to calculate the survival probability of quantum walkers on a Cayley graph of the cyclic group of size  with absorbing trapped sites. In this section we adapt the exact numeration method to the square lattice to calculate the survival probability. We assume every untrapped site is occupied by a walker. At each step, the
with absorbing trapped sites. In this section we adapt the exact numeration method to the square lattice to calculate the survival probability. We assume every untrapped site is occupied by a walker. At each step, the  walkers perform a classical random walk on the square lattice, for which the probability of finding the particle at site
walkers perform a classical random walk on the square lattice, for which the probability of finding the particle at site  is calculated with the sum of the corresponding probabilities at its nearest neighbor sites divided by four. The survival probability at time t is given by,
is calculated with the sum of the corresponding probabilities at its nearest neighbor sites divided by four. The survival probability at time t is given by,
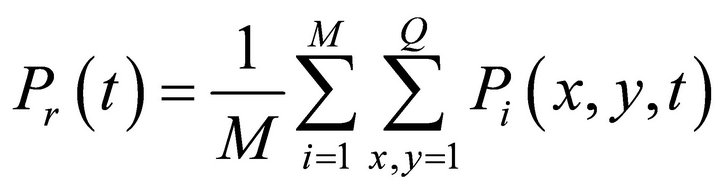 (13)
(13)
Here  enumerates a particular independent initial configuration of the system. Note that
enumerates a particular independent initial configuration of the system. Note that  or
or , where
, where  is the number of traps on the square lattice and
is the number of traps on the square lattice and 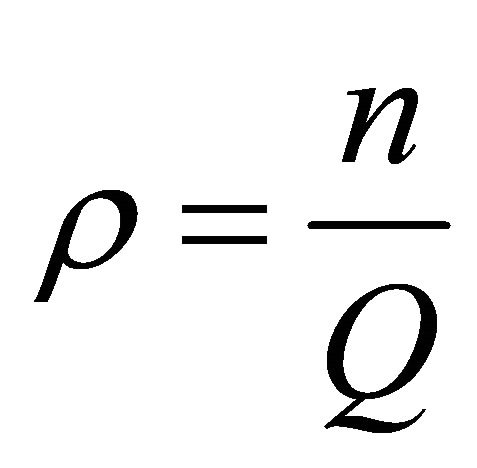 is the trapping density. We take the lattice sites at
is the trapping density. We take the lattice sites at . If site
. If site  is a trapping site, we let
is a trapping site, we let , so that the summation above is not restricted to the untrapped sites. We also assume that the initial configurations on the walkers are such that the
, so that the summation above is not restricted to the untrapped sites. We also assume that the initial configurations on the walkers are such that the 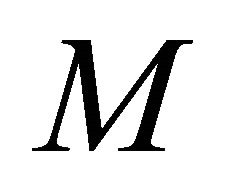 walkers occupy all the untrapped sites. To account for randomization we calculate the mean survival probability,
walkers occupy all the untrapped sites. To account for randomization we calculate the mean survival probability,
 (14)
(14)
where  denotes the number of different configurations. Recall we assumed the
denotes the number of different configurations. Recall we assumed the  walkers are distinguishable and uncorrelated, so the evolution of the Mparticle walk is equivalent to a single-particle walk with an ensemble of initial configurations. So by quantum computation of the single-particle distribution, the classical survival probability is useful.
walkers are distinguishable and uncorrelated, so the evolution of the Mparticle walk is equivalent to a single-particle walk with an ensemble of initial configurations. So by quantum computation of the single-particle distribution, the classical survival probability is useful.
4. Numerical Analysis of the Survival Probability of M-Walkers with Phase Parameters
In this section we numerically analyze the dynamics of the survival probability in the two-dimensional multiparticle quantum walk with phase parameters. Firstly, we investigate the survival probability for three different initial states with fixed phase parameters. Initial chirality states of untrapped cites are chosen as in the first case,  , in the second case
, in the second case  sequentially and in the last case, randomly chosen either of
sequentially and in the last case, randomly chosen either of  or
or . We call them left, sequential and mixed initializations respectively. In numeric simulations, the number of sites on the square lattice is taken to be
. We call them left, sequential and mixed initializations respectively. In numeric simulations, the number of sites on the square lattice is taken to be . To account for random distribution of traps, a statistical configurational average of the mean survival probability is calculated over different independent realizations of the initial system with
. To account for random distribution of traps, a statistical configurational average of the mean survival probability is calculated over different independent realizations of the initial system with  different configurations. We should remark that the coin operator governing the walk is given by
different configurations. We should remark that the coin operator governing the walk is given by , where
, where  is a two-dimensional generalization of the Fibonacci operator and
is a two-dimensional generalization of the Fibonacci operator and  is the diagonal phase adjustment (see Section 2 for details).
is the diagonal phase adjustment (see Section 2 for details).
Survival probability of QW are plotted in Figures 1(a)-(c) for left, sequential and mixed initializations and for different trap densities  and
and 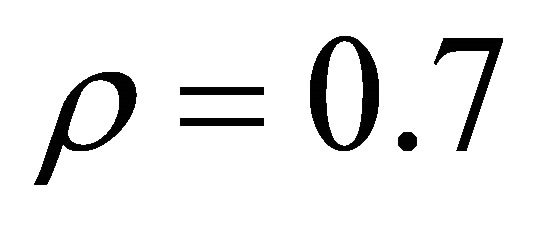 with arbitrary fixed phase parameters
with arbitrary fixed phase parameters . Figures are plotted in the double logarithmic scale. We see that the survival probability decreases in time and is less at higher trap densities. All different initializations show same behavior and the survival probability is seen to exhibit a linear dependence on time in the double logarithmic scale. When we fit the lines to the curves in the time regime, line fits obey the Kohlrausch-Williams-Watts stretched exponential function [19] which is given by,
. Figures are plotted in the double logarithmic scale. We see that the survival probability decreases in time and is less at higher trap densities. All different initializations show same behavior and the survival probability is seen to exhibit a linear dependence on time in the double logarithmic scale. When we fit the lines to the curves in the time regime, line fits obey the Kohlrausch-Williams-Watts stretched exponential function [19] which is given by,
 (15)
(15)
where exponent  determines the decay rate of the sur-
determines the decay rate of the sur-

Figure 1. The time dependence of the survival probability in the QW for trap densities  phase parameters
phase parameters 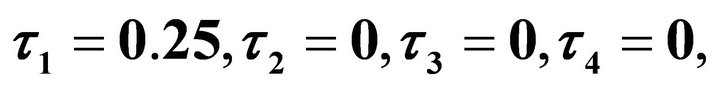 with the initializations (a) left, (b) sequential, (c) mixed.
with the initializations (a) left, (b) sequential, (c) mixed.
vival probability. Figure 1 shows that the survival probability of the Fibonacci walk with phase parameters evaluate with time as stretched exponential obey to Equation (1). As it can be seen form Figure 1, there’s no qualitatively different dynamical regime in decay of the survival probability of the quantum walk for long time regime. Whereas, in Ref. [12], authors have found that the time decay of the survival probability of the Hadamard walk in the trapped space has qualitatively different dynamical regime for different initial configuration of the walker states. They have explained the time crossover behavior in dynamical regime as transition from Rosenstock to the Donkser and Varadhan regime. In short time regime in Figure 1, the numerical error appears which may probably cause from insufficient statistical average due to lack of computational ability of our personal computer. If the time crossover was being in the survival probability it would be appear for example at the trap density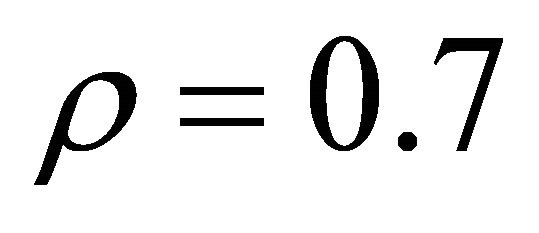 . Indeed, the survival probability curves for all trap densities and different initial configurations systematically show the linear behavior in the double logarithmic scale for relatively long time regime. Furthermore, the numerical anomaly of the survival probability lines in the short time regime can be affected by the phase parameter
. Indeed, the survival probability curves for all trap densities and different initial configurations systematically show the linear behavior in the double logarithmic scale for relatively long time regime. Furthermore, the numerical anomaly of the survival probability lines in the short time regime can be affected by the phase parameter . On the other hand, Figure 1 does not clearly give any information about depending of the decay parameters
. On the other hand, Figure 1 does not clearly give any information about depending of the decay parameters  on phase parameters while it gives some information about depending of the exponent
on phase parameters while it gives some information about depending of the exponent  on the trap density
on the trap density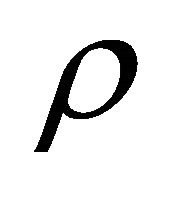 . Therefore, in order to clarify the trap density dependence of the decay rate
. Therefore, in order to clarify the trap density dependence of the decay rate  for different initializations and fixed phase parameters,
for different initializations and fixed phase parameters,  is plotted versus the trap density
is plotted versus the trap density  in Figure 2. It can be seen from this figure that stretched exponential parameter
in Figure 2. It can be seen from this figure that stretched exponential parameter  of the survival probability of quantum walk depends on trap density. Indeed it exhibits almost a linear dependence on trap density for all different initializations and fixed phase parameters
of the survival probability of quantum walk depends on trap density. Indeed it exhibits almost a linear dependence on trap density for all different initializations and fixed phase parameters 
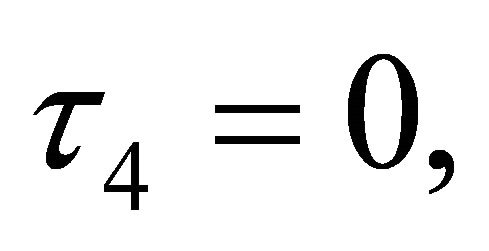 . Clearly
. Clearly  increases with increasing trap density. Similar behavior for Hadamard walk on the one dimensional randomly trapped lattice has been observed in the Donkser and Varadhan regime in Ref. [12].
increases with increasing trap density. Similar behavior for Hadamard walk on the one dimensional randomly trapped lattice has been observed in the Donkser and Varadhan regime in Ref. [12].
In order to further investigate and clarify the phase parameter dependence of the decay parameter  we will consider different phase combination for quantum walk on the two dimensional randomly trapped lattice. However here we have considered only left initialization since it has been shown in Figures 1 and 2 that the stretched exponential parameter
we will consider different phase combination for quantum walk on the two dimensional randomly trapped lattice. However here we have considered only left initialization since it has been shown in Figures 1 and 2 that the stretched exponential parameter  of survival probability almost linearly increases with increasing trap density for all initializations at fixed phase parameters. For four different combination of the parameter, the time dependence of the survival probability of quantum walk has been plotted in Figures 3(a)-(d) in the double logarithmic scale for several trap densities. For the trap den-
of survival probability almost linearly increases with increasing trap density for all initializations at fixed phase parameters. For four different combination of the parameter, the time dependence of the survival probability of quantum walk has been plotted in Figures 3(a)-(d) in the double logarithmic scale for several trap densities. For the trap den-
 in the cases of the left, sequential and mixed initializations.
in the cases of the left, sequential and mixed initializations.
 ; (d)
; (d) .
.
sities 
 and
and , we have chosen different phase parameter combinations in Figure 3(a) as
, we have chosen different phase parameter combinations in Figure 3(a) as , in Figure 3(b) as
, in Figure 3(b) as , in Figure 3(c) as
, in Figure 3(c) as  and finally in Figure 3(d) as
and finally in Figure 3(d) as . As it can be seen from all subfigures of Figure 3, the time behavior of the survival probability of the Fibonacci walks with different phase combination on the trapped space obey to stretched exponential law. Furthermore, this figures also shows that time dependence of the survival probability of walks are affected by phase combinations. Indeed, it clearly seems that the survival probability curves in Figures 3(a) and (b) are quite different that of Figures 3(c) and (d). To see the phase parameter dependence of the stretched exponential parameter
. As it can be seen from all subfigures of Figure 3, the time behavior of the survival probability of the Fibonacci walks with different phase combination on the trapped space obey to stretched exponential law. Furthermore, this figures also shows that time dependence of the survival probability of walks are affected by phase combinations. Indeed, it clearly seems that the survival probability curves in Figures 3(a) and (b) are quite different that of Figures 3(c) and (d). To see the phase parameter dependence of the stretched exponential parameter , we have plotted survival probability for the different phase combinations at fixed trap densities in Figure 4. As it can be seen that the slopes of the survival probability curves for the three different phase combination fixed density
, we have plotted survival probability for the different phase combinations at fixed trap densities in Figure 4. As it can be seen that the slopes of the survival probability curves for the three different phase combination fixed density  in Figure 4(a). For example, while the curves for the phase combinations
in Figure 4(a). For example, while the curves for the phase combinations  and
and  are almost coincident, they are quite different for the phase combinations
are almost coincident, they are quite different for the phase combinations  and
and . Similar behavior for different phase combination at fixed trap density value
. Similar behavior for different phase combination at fixed trap density value  appears in Figure 4(b). These numerical results demonstrate that the stretched exponential parameter
appears in Figure 4(b). These numerical results demonstrate that the stretched exponential parameter  of the survival probability of the quantum walks depends on the combination of the phase parameters.
of the survival probability of the quantum walks depends on the combination of the phase parameters.
In Figure 5 the phase parameter dependence of the  is given for several combinations of the phase parameters which used in Figures 3 and 4. As it can be seen this
is given for several combinations of the phase parameters which used in Figures 3 and 4. As it can be seen this

Figure 4. The time dependence of the survival probability in the QW for different phase parameters and fixed trap densities (a) ; (b)
; (b) 

Figure 5. The time dependence of the decay parameters  on the trap density
on the trap density  for different phase parameters.
for different phase parameters.
figure that the decay parameter  dramatically changes due to phase combination. For all different phase parameters the decay parameter
dramatically changes due to phase combination. For all different phase parameters the decay parameter  almost linearly increases with increasing trap density.
almost linearly increases with increasing trap density.
These results show that the phase variables of the coin operator of walkers can be used as an control parameter to adjust the decay rate of the survival probability of the quantum walk on the trapped lattice for all initial states of walkers.
5. Conclusion
In this study, the coin operator was taken to be a parametrization of the usual quantum walk governed by a two-dimensional generalization of the Fibonacci operator and by adapting the exact numeration method of Havlin et al. [18] we have calculated the survival probability in a two-dimensional quantum walk with phase parameters on a trapped lattice. We have shown that the survival probability of the quantum walk decays with time obey to the stretched exponential law for all initial states of walkers. On the other hand we have shown that stretched exponential decay parameter  can be arranged by phase parameter combination. Obtained numerical results provide that phase parameters can be used as an control parameter to determine the decay rate of the survival probability of the quantum walk.
can be arranged by phase parameter combination. Obtained numerical results provide that phase parameters can be used as an control parameter to determine the decay rate of the survival probability of the quantum walk.
6. Acknowledgements
This work was partially supported by the Istanbul University under Project No: 28432.