1. Introduction
The Lambert W function, named after Johann Heinrich Lambert [1], is a standard function in both Mathematica, where it’s called Product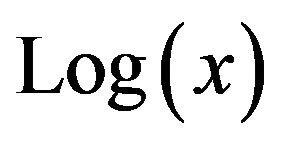 , and in Maple, where you can use both Lambert
, and in Maple, where you can use both Lambert  or Lambert
or Lambert . The zero in this latter expression denotes the principal branch of the inverse of
. The zero in this latter expression denotes the principal branch of the inverse of . The actual usage of the letter W has a rather vague origin. One source attributes it to some earlier papers on the subject that wrote the standard equation as
. The actual usage of the letter W has a rather vague origin. One source attributes it to some earlier papers on the subject that wrote the standard equation as  using a small w. Programming protocol with Maple then forced the letter to be capitalized [2]. Another source [3] attributes the W to honor the British mathematician Sir Edward M. Wright (famous co-author with G. H. Hardy of An Introduction to the Theory of Numbers) who did a lot of pioneering work with the function. Finally, Robert Corless and David Jeffrey of the University of Western Ontario have written, during the past several decades, a number of journal articles on the function. Their paper in 1996, in collaboration with Gaston Gonnet, David Hare, and Donald Knuth, was where Lambert’s name got attached to the function [2]. It could have been coined the Euler W function, since Euler had studied the equation
using a small w. Programming protocol with Maple then forced the letter to be capitalized [2]. Another source [3] attributes the W to honor the British mathematician Sir Edward M. Wright (famous co-author with G. H. Hardy of An Introduction to the Theory of Numbers) who did a lot of pioneering work with the function. Finally, Robert Corless and David Jeffrey of the University of Western Ontario have written, during the past several decades, a number of journal articles on the function. Their paper in 1996, in collaboration with Gaston Gonnet, David Hare, and Donald Knuth, was where Lambert’s name got attached to the function [2]. It could have been coined the Euler W function, since Euler had studied the equation  [4] (although Euler credits Lambert as studying the equation first [5]), but they decided Euler had enough items attached to his name!
[4] (although Euler credits Lambert as studying the equation first [5]), but they decided Euler had enough items attached to his name!
2. Definition
The exponential function  is defined for all real x, but has a codomain of
is defined for all real x, but has a codomain of . This function (Figure 1(a)) is the product of two elementary functions, each defined on the entire real line, and each being one-to-one; but the product is not injective. Consequently, if we restrict the domain to
. This function (Figure 1(a)) is the product of two elementary functions, each defined on the entire real line, and each being one-to-one; but the product is not injective. Consequently, if we restrict the domain to , then
, then  will possess an inverse, which is a function, and it’s this function that is now known as the (principal) Lambert W function (Figure 1(b)), written as
will possess an inverse, which is a function, and it’s this function that is now known as the (principal) Lambert W function (Figure 1(b)), written as . An alternative branch for W would be defined for that portion of
. An alternative branch for W would be defined for that portion of  when
when . We won’t consider that situation in this article.
. We won’t consider that situation in this article.
Several function values of W are easy to computesuch as .
. and
and . The value of
. The value of , known as the omega constant, has the approximate value 0.567143. The number
, known as the omega constant, has the approximate value 0.567143. The number  is, in some sense, a distant cousin of the golden ratio
is, in some sense, a distant cousin of the golden ratio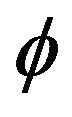 , since
, since 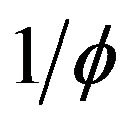 is a solution to
is a solution to , and
, and 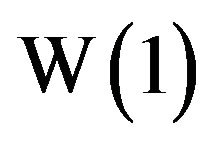 is the solution to
is the solution to , and
, and  is the linear Maclaurin approximation to
is the linear Maclaurin approximation to  (Figure 2). Since W is the inverse of
(Figure 2). Since W is the inverse of , it follows that
, it follows that  and that the slope of the curve in Figure 1(b) at the point
and that the slope of the curve in Figure 1(b) at the point
 is
is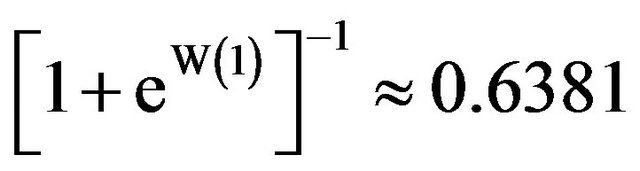 .
.
3. Computation
A natural question is how to compute arbitrary values of . One result, from the Lagrange inversion theorem, asserts that the Lambert W function has the Taylor series expansion [6,7]
. One result, from the Lagrange inversion theorem, asserts that the Lambert W function has the Taylor series expansion [6,7]
 (1)
(1)
which, unfortunately, has a radius of convergence of merely . Since the denominator n! grows rapidly it’s
. Since the denominator n! grows rapidly it’s
advantageous to write the series with the coefficients defined recursively as , with
, with
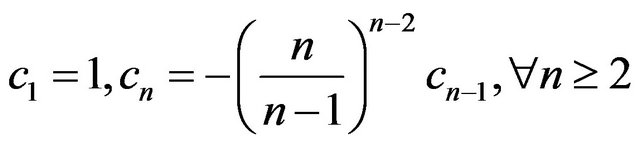 . This recursion lends itself to easy programming evaluation. Testing this, with say a series of 150 terms (which is plenty, considering that
. This recursion lends itself to easy programming evaluation. Testing this, with say a series of 150 terms (which is plenty, considering that ), with
), with , we obtain a partial sum value of
, we obtain a partial sum value of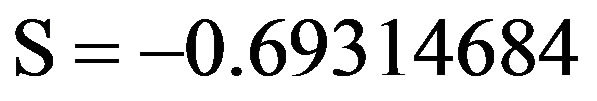 , which differs from the exact value of
, which differs from the exact value of  by 0.0000003. We also note that
by 0.0000003. We also note that , so the use of the series is justified.
, so the use of the series is justified.
On the other hand, a TI-graphing calculator returns “overflow error” if we try to determine , primarily since the coefficients grow rapidly.
, primarily since the coefficients grow rapidly.
Suppose that  and we wish to compute
and we wish to compute .
.
One possibility is the series
 (2)
(2)
where  and
and
 denotes a Stirling number of the first kind [3]. The series (2) is somewhat impractical to use because of the difficulty in determining
denotes a Stirling number of the first kind [3]. The series (2) is somewhat impractical to use because of the difficulty in determining ; it turns out to be more useful to employ some standard numerical schemes for approximating
; it turns out to be more useful to employ some standard numerical schemes for approximating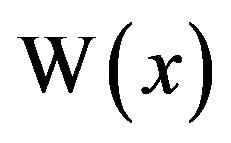 .
.
First, setting , we need to solve
, we need to solve . Defining the function g by
. Defining the function g by , we use Newton’s method to approximate y in
, we use Newton’s method to approximate y in . This gives
. This gives . To determine
. To determine
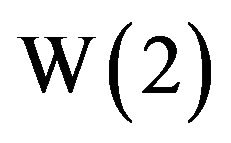 , for example, starting with an initial approximate of
, for example, starting with an initial approximate of , after 7 more iterations we get
, after 7 more iterations we get  , which is an excellent approximation to
, which is an excellent approximation to  because
because  returns 2 on the calculator. If x is a relatively small number, then an initial approximate of 0 will suffice for the algorithm; but if x is large, then ln x can be chosen for
returns 2 on the calculator. If x is a relatively small number, then an initial approximate of 0 will suffice for the algorithm; but if x is large, then ln x can be chosen for . For instance, if
. For instance, if , choose
, choose , and after 5 iterations we get W(10) ≈ 1.745528003.
, and after 5 iterations we get W(10) ≈ 1.745528003.
Newton’s method is a favorite iteration scheme for many because of its simplicity, though the convergence, quadratic in general, is typically relatively slow. A faster choice is furnished by Halley’s method (of Halley’s comet fame), which produces cubic convergence, and happens to be the choice implemented by the software Maple; this scheme gives [8]

Employing this gives W(10) ≈ 1.745528003 after 3 iterations. This complex looking scheme is actually what you get when you apply Newton’s method to the function
 [9]. An alternative root-finding scheme, using continued fraction expansion, is described in [10].
[9]. An alternative root-finding scheme, using continued fraction expansion, is described in [10].
4. Calculus
We know that since  is an increasing and differentiable function for all
is an increasing and differentiable function for all  then its inverse
then its inverse  is likewise increasing and differentiable for all
is likewise increasing and differentiable for all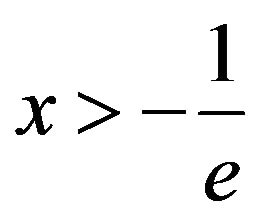 .
.
Differentiating this latter equation with respect to y, we obtain
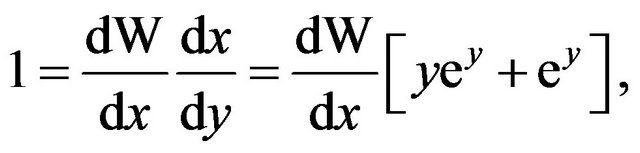
so
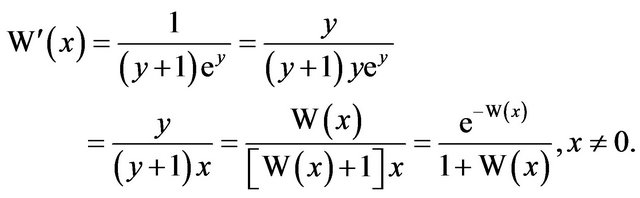 (3)
(3)
In particular, 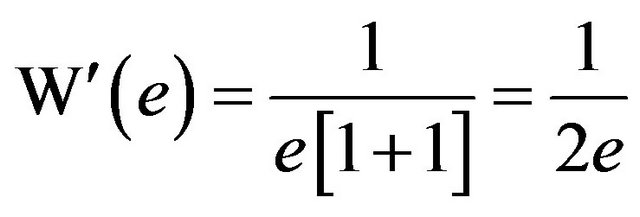 , and similarly,
, and similarly, . What about
. What about  the right-hand side of (3) is indeterminant at
the right-hand side of (3) is indeterminant at , but division of both sides of (1) by x and taking the limit as
, but division of both sides of (1) by x and taking the limit as  give
give
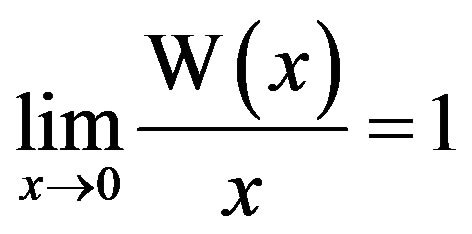 . This yields
. This yields

For large x, the graph of 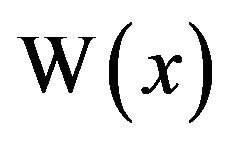 bears strong resemblance to
bears strong resemblance to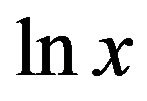 , since from (2) we have
, since from (2) we have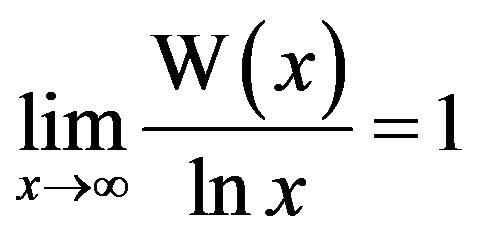 although we have to be careful here because the difference
although we have to be careful here because the difference  increases without bound as
increases without bound as 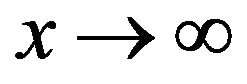 [7]. The graph of
[7]. The graph of , like that of
, like that of , is concave downward for all x since
, is concave downward for all x since  is concave upward. If we differentiate (3), and omit the argument x for brevity, then
is concave upward. If we differentiate (3), and omit the argument x for brevity, then

Rewriting  as
as 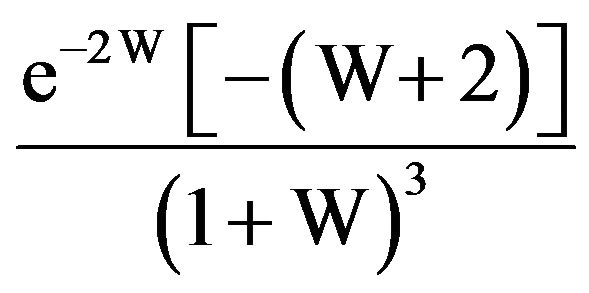 puts this into the form which fits the general case for
puts this into the form which fits the general case for 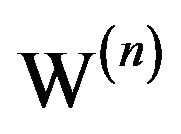 [5]. In fact, from this form, we readily see that there is a point of inflection on the curve when
[5]. In fact, from this form, we readily see that there is a point of inflection on the curve when , which actually falls on the other branch of the W function.
, which actually falls on the other branch of the W function.
Continuing along the calculus vein, we should examine, if possible, the integral of . To this end, recall that
. To this end, recall that  iff
iff . Thus,
. Thus,
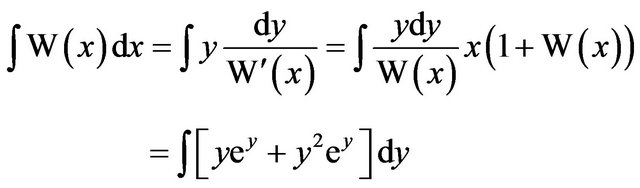
and integrating this last integral by parts, we obtain
 , which now gives
, which now gives
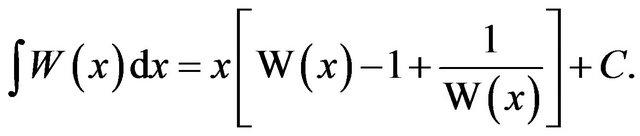 (4)
(4)
In particular, the area of the region bounded by the curve , the x-axis, and the line
, the x-axis, and the line 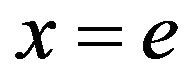 is, therefore,
is, therefore,

We note this result agrees with evaluating the integral via inverse functions [11], because then
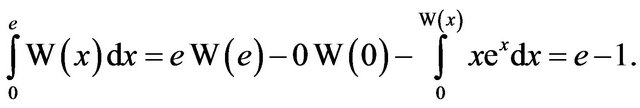
Other integrals, involving functions containing W, can be computed, some just with a special change of variable [6]. For instance,
 .
.
The function  is concave up, connecting
is concave up, connecting 
and , hence its area
, hence its area  is less than
is less than . Similarly we find
. Similarly we find
 , and this is greater than
, and this is greater than  since
since  is increasing and concave down from
is increasing and concave down from to
to .
.
5. Applications
An article appeared in the February, 2000, issue of FOCUS, the newsletter of the Mathematical Association of America, touting the merits of the W function as a candidate for a new elementary function to be studied in schools and to be included in textbooks [12]. The rationale for this was that not only is W a radically different function from the traditional elementary functions of polynomials, rationals, exponentials, logarithmics, and trigonometrics, but its calculus provides a wealth of interesting, and powerful, applications. A number of these are mentioned in a paper by Corless et al., where they describe such applications as enumeration of trees, combustion, enzyme kinetics, linear delay equations, population growth, spread of disease, and the analysis of algorithms [3]. An article [13] by Packel and Yuen shows that W is instrumental in determining the maximum range for a projectile with linear resistance (problems of this type have certainly been important for several thousand years). The solution for the current in a series diode/resistor circuit can also be written in terms of W. Applications of W are found in complex cases involving atomic, nuclear, and optical physics. The first physics problem to be solved explicitly in terms of W was one in which the exchange forces between two nuclei within the hydrogen molecular ion  were calculated [14]. Several other cases involve generalized Gaussian noise, solar winds, black holes, general relativity, quantum chromodynamics, fuel consumption, Stirling’s formula for n!, cardiorespiratory control, water-wave heights in oceanography, enumeration of trees in combinatorics, and statistical mechanics [5,15-17]. A really interesting analog of
were calculated [14]. Several other cases involve generalized Gaussian noise, solar winds, black holes, general relativity, quantum chromodynamics, fuel consumption, Stirling’s formula for n!, cardiorespiratory control, water-wave heights in oceanography, enumeration of trees in combinatorics, and statistical mechanics [5,15-17]. A really interesting analog of  is given by Dan Kalman [18], where he defines a function glog, similar to W, in that glog is the inverse to
is given by Dan Kalman [18], where he defines a function glog, similar to W, in that glog is the inverse to . The glog function bears a strong resemblance to W, possessing similar properties and useful common applications, such as solving exponential-linear equations. The two functions are intimately related by
. The glog function bears a strong resemblance to W, possessing similar properties and useful common applications, such as solving exponential-linear equations. The two functions are intimately related by
 and
and .
.
In the remainder of this article I wish to focus on a couple of applications dealing with ordinary algebraic equation solving.
6. Algebra
In a high-school precalculus course one might be presented with the elementary equation  to solve. Now, instead, let’s solve a similar equation
to solve. Now, instead, let’s solve a similar equation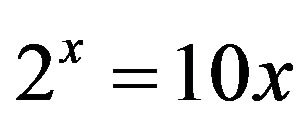 , which means that it won’t suffice to begin by taking the logarithm of both sides. Instead, we proceed as follows:
, which means that it won’t suffice to begin by taking the logarithm of both sides. Instead, we proceed as follows:

Since the right-hand side of this last equation is of the form , and since we know
, and since we know 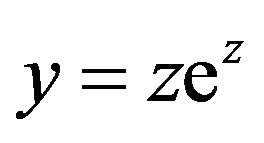 iff
iff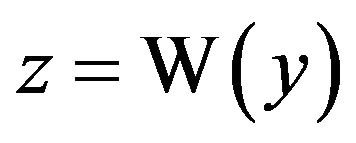 then
then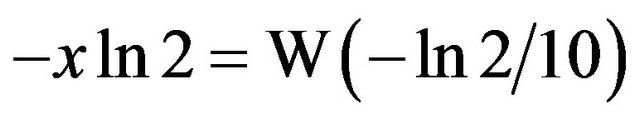 , or
, or .
.
Using Kalman’s glog function we can solve 
and get . Since
. Since
 we can use (1) to approximate
we can use (1) to approximate  and get −0.0746900848, so x = 0.1077550149. Checking, we find 2x = 1.07755015 = 10x.
and get −0.0746900848, so x = 0.1077550149. Checking, we find 2x = 1.07755015 = 10x.
The equation 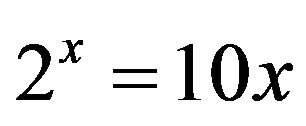 is a special case of a more general setting
is a special case of a more general setting , where we assume the base
, where we assume the base  and where neither b nor d equals zero. The substitution
and where neither b nor d equals zero. The substitution  then gives
then gives
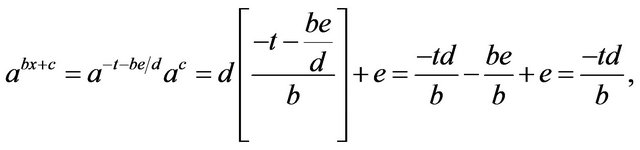
and, thus,

Multiplication of both sides by  gives
gives
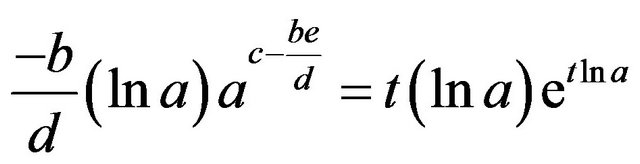 , which now has the form
, which now has the form , so
, so 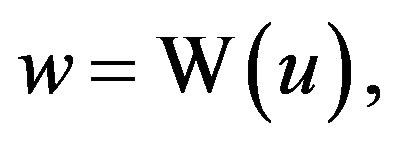 or
or 
and, hence,

that is, 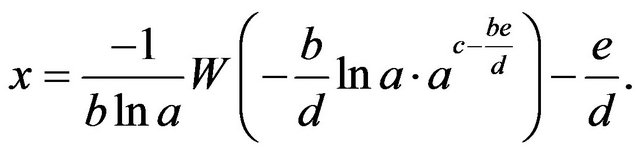
Another interesting algebraic application involves the infinite tower of exponents , which will be denoted by
, which will be denoted by . To solve the particular equation
. To solve the particular equation  one might argue that this is equivalent to
one might argue that this is equivalent to , in which case we have
, in which case we have , so
, so , which is the correct solution to
, which is the correct solution to  But what about T(x) = 3, T(x) = 4, or T(x) = y. It stands to reason that as y increases, so does x. But with
But what about T(x) = 3, T(x) = 4, or T(x) = y. It stands to reason that as y increases, so does x. But with , we can write this as
, we can write this as , or
, or , so
, so 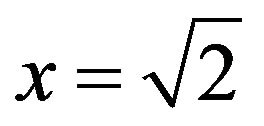 again! Something isn’t right.
again! Something isn’t right.
The problem lies with the domain of T. We find in [19] that the infinite tower of exponents is only defined (i.e.its interval of convergence) for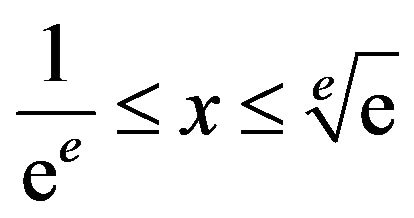 , or approximately
, or approximately . So if x is selected from this interval, what is
. So if x is selected from this interval, what is ? If we set
? If we set  then
then
 .
.
Note also that  when
when , and the above expression for y gives a function continuous at
, and the above expression for y gives a function continuous at since
since . Hence, if
. Hence, if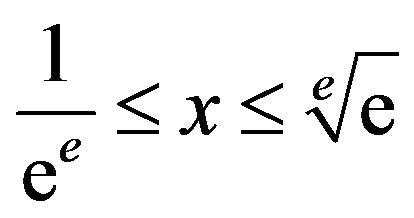 , then
, then , so
, so , and this is why the equation
, and this is why the equation  is solvable, but
is solvable, but  is not.
is not.
The graph of T is therefore an increasing function with domain 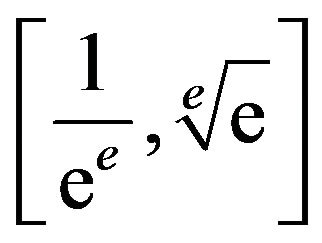 and range
and range . It also passes through the two obvious points of
. It also passes through the two obvious points of
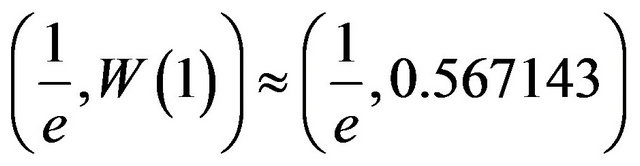 and
and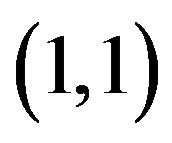 . What else can we deduce? Checking for differentiability, we have from (3),
. What else can we deduce? Checking for differentiability, we have from (3),

and since the limit of this expression is 1 as , then
, then , and hence
, and hence  is never 0, so T is always strictly increasing. The following small table (Table 1) of values will prove helpful.
is never 0, so T is always strictly increasing. The following small table (Table 1) of values will prove helpful.
Alternatively, we could have found 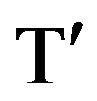 by implicit differentiation of
by implicit differentiation of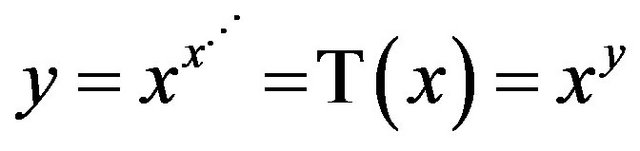 . Thus
. Thus
 or
or ; so again
; so again
 . Use of this form for easier access to
. Use of this form for easier access to  then gives, after some algebraic manipulations and cancellations,
then gives, after some algebraic manipulations and cancellations,

This complex expression appears to yield negative values for all  and positive values for all
and positive values for all , and
, and . Hence, we have an inflection point at
. Hence, we have an inflection point at . Also
. Also
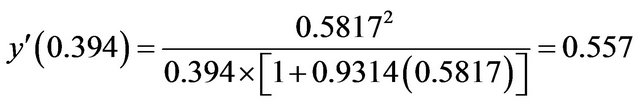 . Putting all of these pieces of the puzzle together, we obtain a decent graph of T, as shown in Figure 3.
. Putting all of these pieces of the puzzle together, we obtain a decent graph of T, as shown in Figure 3.
The tower function T must necessarily possess an inverse . We note then that
. We note then that
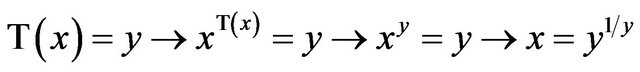
and, consequently, this inverse is . Composition of the two functions give the interesting pair of identities,
. Composition of the two functions give the interesting pair of identities,
