Runge-Kutta Schemes Coefficients Simulation for Comparison and Visual Effects ()
1. Introduction
The versatility of Runge-Kutta scheme as a numerical tool in engineering (most especially nonlinear dynamics) is well acknowledged among researchers in this field. [1] has employed Runge-Kutta scheme in modelling Lorenz system. In the authors’ paper, the classical fourth-order Runge-Kutta was modified to obtain new methods which are of order five. These techniques were tested on the Lorenz system involving chaotic and nonchaotic characteristics. The results obtained shows that Lorenz model is highly sensitive to the initial conditions of the system. The paper concluded that modified fifth-order RungeKutta method appears to be the best method to approximate Rayleigh-Benard convection. This is attributed to its high accuracy. [2] has also demonstrated the versatility of the Runge-Kutta scheme. In their paper, an em-
bedded Runge-Kutta with orders 3 and 4 with the aim to deliver an estimation of the local error for adaptive stepsize control purposes in the interaction picture method. The results of their study showed that the embedded Runge-Kutta method 4(3) with interaction picture preserves the features of the RK4-IP method and provides a local error estimate at no significant cost. The outcome of their study is of immense advantage in step-size control in the interaction picture method. A recent developed Runge-Kutta scheme has been applied in non-slip rolling [3]. This method is referred to as Accelerated RungeKutta Methods (ARM). This method benefits from precise parameter selection technique that increases their order of accuracy for some problems. The paper showed that an efficient and effective Accelerated Runge-Kutta Method capable of modelling complex nonlinear mechanical systems has been developed. A parametric study of nonlinear beam vibration resting on linear elastic foundation was carried out by [4]. A well known Duffing oscillator was analyzed numerically using Runge-Kutta scheme. The result of the study shows that the stretching potential energy was responsible for generating the cubic nonlinearity in the system dynamic. A low-dispersion and low-dissipation implicit Runge-Kutta has been introduced by [5]. This new implicit Runge-Kutta scheme is of great advantage because high order accuracy is achieved with fewer stages when compared to the standard explicit Runge-Kutta schemes. This method has high application potentials in wall-bounded flows with solid boundaries in the computation as well as sound generation by reacting flows. Visual tools have in no small measure contributed immensely in exploring dynamics of nonlinear systems. [6] carried out a study on the visual effects of filtered chaotic signals. It was understood from the paper that filtered chaotic signals is capable of exhibiting an increase in observed fractal dimension. The approach towards providing an interesting insight into this dynamic is through the use of computer animation and three-dimensional ray-tracings. [7] in his paper reported how fuzzy dynamic system can illustrate chaotic phenomena and chaotic dynamics in comparison to other nonlinear systems. It is concluded from the paper that fuzzy chaotic dynamic model of a cubic map results in the same (visual effects) as bifurcation diagrams, and that it reveals stable equilibrium points, periodic-doubling and chaotic attractors. This study has extensively justified the numerous benefits of visual effects. The possibilities for describing sitting postural control using nonlinear method have been investigated by [8] during a long-term driving. The results obtained show that contrary to conventional analysis procedures, nonlinear measures demonstrated the capability of identifying a threshold behaviour describing the change in discomfort. The visual recurrence plots showed an outstanding change in the underlying dynamics after one hour of driving. [9] explained that the challenge of many other methods used for analyzing chaotic systems was that they depicts local nature and exhibited only limited information about a group of parameters. This challenge motivated these authors in exploring visualization technique on the basis of Mandelbrot set methodology. This help immensely in giving the overall view of chaotic systems dynamic performance in the parameter space. A periodic parametric perturbation has been designed for controlling and chaotification from a three-dimensional autonomous system [10]. Lyapunov exponents and bifurcation diagram were used as visual aids for explaining the abundant dynamic characteristics of a three-dimensional system. The authors’ paper has shown that when there is a small parametric perturbation, highly unique dynamic system behaviour will be experienced. A 4-dimensional Chua system has been characterized by [11] using Lyapunov exponent diagrams. With the introduction of a feedback controller into the system, both the largest and the second largest Lyapunov exponents were considered in Lyapunov exponent diagrams. [12] reported that in exploring the nonlinear dynamics of a periodically Driven Duffing resonator coupled to a Van der pol oscillator, bifurcation diagram was adopted as the visual aids. The behaviour of the coupled system as well as the dependence of the system dynamics on the parameter have been studied using bifurcation analysis. [13] focused on simulation and visualisation of chaotic systems. The study implemented fundamental algorithms from the field of chaotic system dynamics such as the reconstruction of the system trajectory in the appropriate embedding space, and the estimation of Lyapunov exponents and the fractal dimension. The bifurcation diagrams produced provides a significant visual effect for identifying chaotic regions in the parameter space.
Although the available literature on the use of RungeKutta scheme for engineering applications is inexhaustible; the dearth of relevant literature bordering on visual impression possibility among different schemes coefficients is a subject of concern. This strongly motivated the present study of the third and fourth order schemes.
2. Methodology
[14] refers, the numerical method of Runge-Kutta is devoted to solving ordinary differential equations of the general form given by Equation (1). However the step by step numerical solution of Equation (1) is given by Equation (2), with  being an incremental weighting function. The general form for
being an incremental weighting function. The general form for  is given by Equation (3). According to Equation (3), the slope estimate of
is given by Equation (3). According to Equation (3), the slope estimate of  is used to extrapolate from an old value
is used to extrapolate from an old value 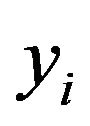 to a new value
to a new value  over a step size h.
over a step size h.
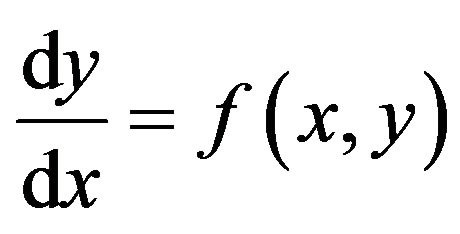 (1)
(1)
 (2)
(2)
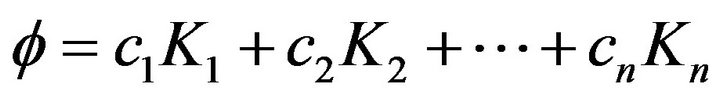 (3)
(3)
The functions  to
to  for the third and fourth order Runge-Kutta schemes are given by Equations (4) to (7). However, the equivalent of Equation (2) for the third and fourth schemes is given respectively by (8) and (9).
for the third and fourth order Runge-Kutta schemes are given by Equations (4) to (7). However, the equivalent of Equation (2) for the third and fourth schemes is given respectively by (8) and (9).
 (4)
(4)
 (5)
(5)
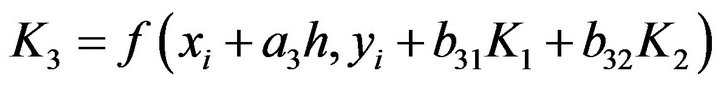 (6)
(6)
 (7)
(7)
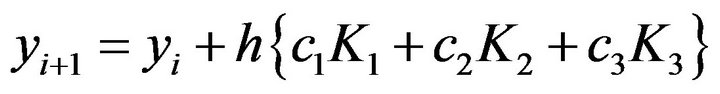 (8)
(8)
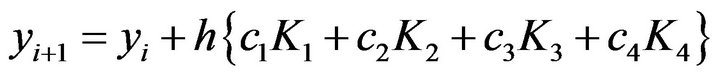 (9)
(9)
[15] executed the tedious computation of the unknown constant coefficients in Equations (4) to (9) using the equivalent relationship with the corresponding coefficients in Taylor series expansion of the function 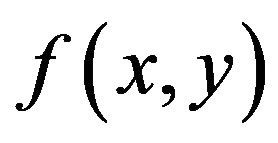 to the nth-order terms. The computation was aided by Butcher simplifying assumption implied by Equation (10).
to the nth-order terms. The computation was aided by Butcher simplifying assumption implied by Equation (10).
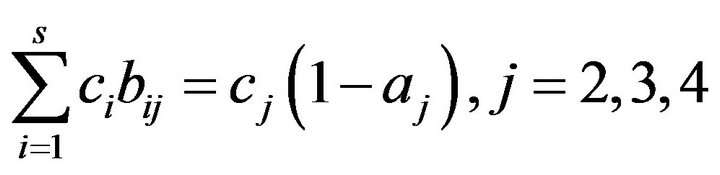 (10)
(10)
As such the coefficients definitions for the third and fourth order schemes are (11) to (16) and (18) to (28) respectively subject to arbitrary choices of 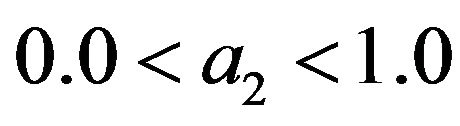 and
and .
.
2.1. Third Order Scheme
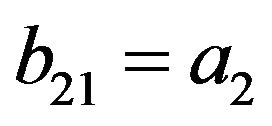 (11)
(11)
 (12)
(12)
 (13)
(13)
 (14)
(14)
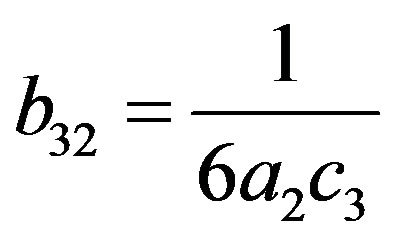 (15)
(15)
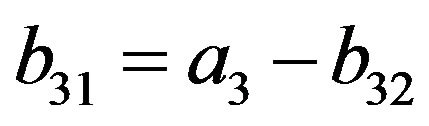 (16)
(16)
The constraint conditions for Equations (11) to (16) are detailed in Equation (17).
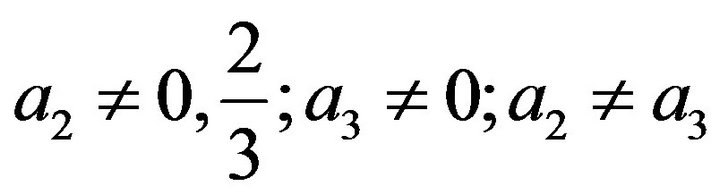 (17)
(17)
2.2. Fourth Order Scheme
 (18)
(18)
 (19)
(19)
 (20)
(20)
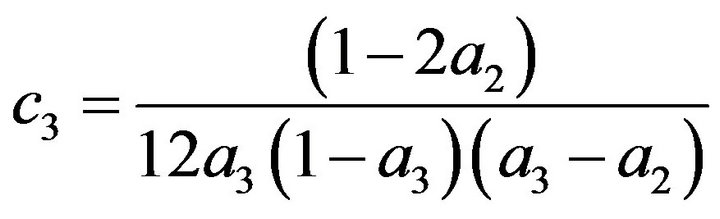 (21)
(21)
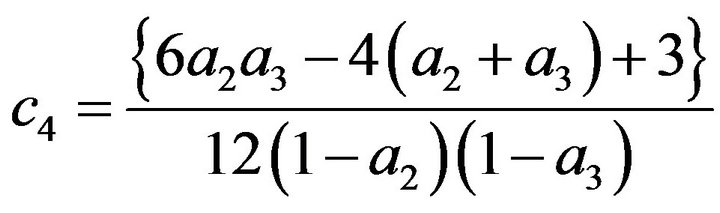 (22)
(22)
 (23)
(23)
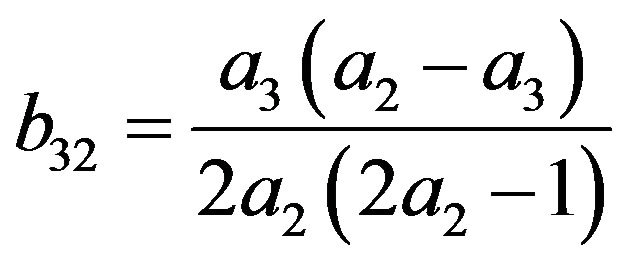 (24)
(24)
 (25)
(25)
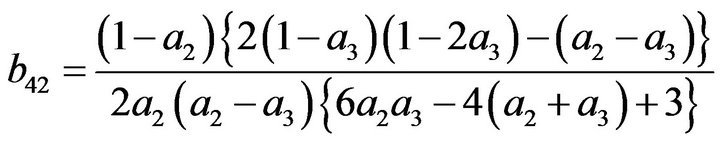 (26)
(26)
 (27)
(27)
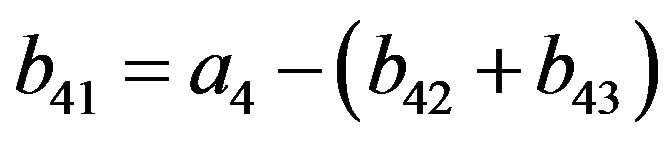 (28)
(28)
The constraint conditions for Equations (18) to (28) are detailed in Equations (29) and (30).
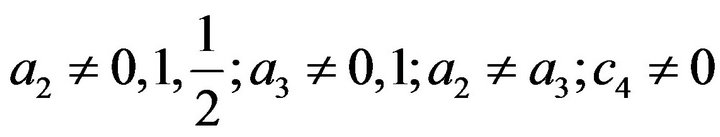 (29)
(29)
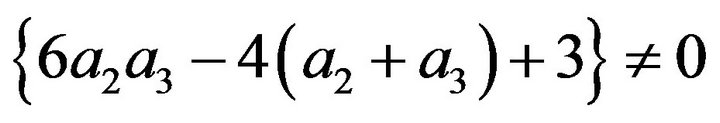 (30)
(30)
2.3. Simulation Parameters
The simulation parameters included arbitrarily selected random number generation seed value of 9876 which drives the random selection of 5000 distinct combination of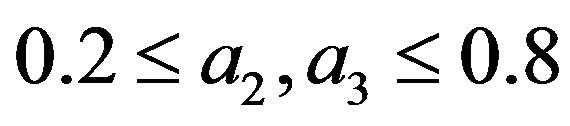 . The success criterion for a trial is that the absolute value of all the coefficients be less or equal to 5.0.
. The success criterion for a trial is that the absolute value of all the coefficients be less or equal to 5.0.
3. Results and Discussions
The simulation results were obtained using FORTRAN 90 while the graphical package is Microsoft Excel 2003. The sample results for the third and fourth order RungeKutta scheme are shown in Tables 1 and 2.
Tables 1 and 2 refers. It is observed that at least one of the coefficients (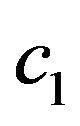 to
to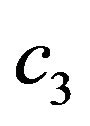 ) require in Equation (8) is less than zero. Similarly, at least one of the coefficients (
) require in Equation (8) is less than zero. Similarly, at least one of the coefficients (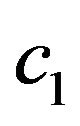 to
to ) require in Equation (9) is also less than zero. However Table 3 shows that none of the two schemes have above three of these coefficients lesser than zero. The percentage of simulation results with two coefficients lesser than zero are respectively 56.88 and 77.10 for third and fourth order schemes. It is interesting to note that both popular third and fourth order RungeKutta schemes belong to none of the coefficients being zero classification.
) require in Equation (9) is also less than zero. However Table 3 shows that none of the two schemes have above three of these coefficients lesser than zero. The percentage of simulation results with two coefficients lesser than zero are respectively 56.88 and 77.10 for third and fourth order schemes. It is interesting to note that both popular third and fourth order RungeKutta schemes belong to none of the coefficients being zero classification.
Figures 1 to 5 show dramatic visual differences between corresponding scatter plots with the exception only in Figure 2 in which the plots almost agreed perfectly. Figures 3 and 4 look visually identical. The visual appearance of Figures 6(a) to (c) resemble distorted saddle which is a manifestation of nonlinear dependence of b41, b42 and b43 on a2, a3 and a4 as independent variables
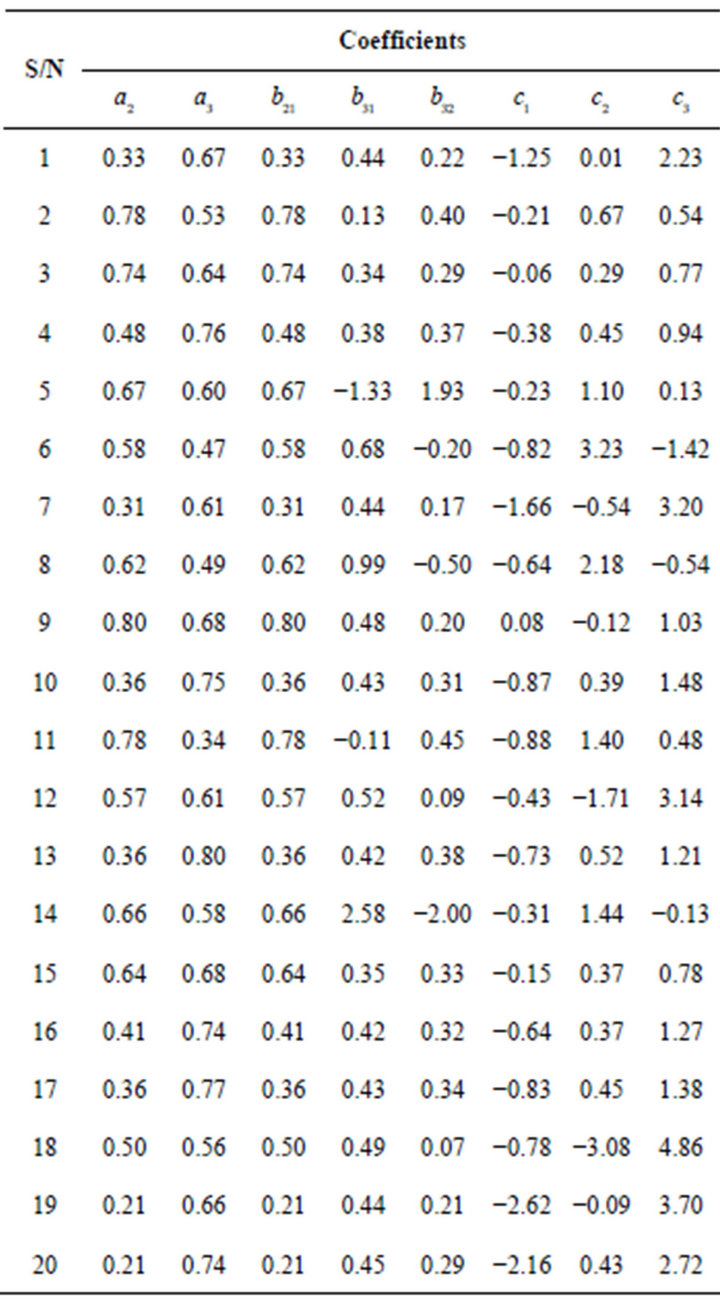
Table 1. Selected simulation results for the third order scheme.
(see Equations (26)-(28)) while there is no corresponding figures for the third order scheme. Similarly Figures 7(b) and (c) look identical to each other while Figure 7(a) is a plane mirror image of Figure 7(b). The region of valid coefficients pair combination is very small compared to total available space region for all the plots in Figures 1 to 7. Despite this space bound constraint majority of the plots are noted for their visual excitement. The observed visual differences in these plots can be a good explanation for the noted computation accuracy potential of fourth scheme over its counterpart third order scheme.
4. Conclusion
This study have shown that the coefficients of the slope estimate for the third and fourth schemes have mix sign for large number of simulated cases. However, none of

Table 2. Selected simulation results for the fourth order scheme.
the two schemes have above three of these coefficients lesser than zero. The percentages of simulation results with two coefficients lesser than zero dominate and are
respectively 56.88 and 77.10 for third and fourth schemes. The popular third and fourth schemes belong to none of the coefficients being zero classification with respective percentage of 0.72 and 3.28 in total simulated cases. The comparisons of corresponding scatter plots are visually exciting. The noted overall visual differences between corresponding scatter plots and distribution results
can be used to justify the accuracy of fourth scheme over its counterpart third scheme.