Topological-Geometrical and Physical Interpretation of the Dark Energy of the Cosmos as a “Halo” Energy of the Schrödinger Quantum Wave ()
1. Introduction, Objective and Background Information
Dark energy is the absolute value of the negative energy of the quantum wave i.e. the quantum surface of the quantum particle and is the cause of negative repulsive gravity while ordinary positive energy which we can measure is the positive or ordinary energy of the quantum particle. The sum of both energies is equal to the energy given by Einstein’s relativity formula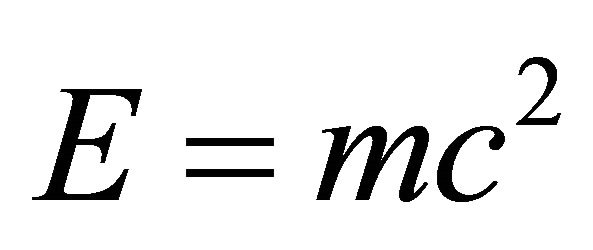 . It is the main objective of the present work to prove the above.
. It is the main objective of the present work to prove the above.
Accurate cosmic measurements over quite a long period of time have revealed beyond reasonable doubt that only 4.5% of the energy contained in the universe, according to the theory of relativity, could be measured directly, while the rest is supposed to be a mysterious kind of “halo” energy which could not be detected using our present measurement technology, if at all. To elucidate this as briefly and as simply as possible, we start by considering a line segment representing a unit interval, which in turn represents a one dimensional idealized “spacetime”. Subsequently we randomly remove parts of this line except for the end points, in a manner reminiscent of what we do when we construct a deterministic middle third Cantor set except for adding uniform randomness to the iteration [1,2]. In the case of the classical Cantor set we end up, after infinitely many iterations, with a Hausdorff dimension amounting to 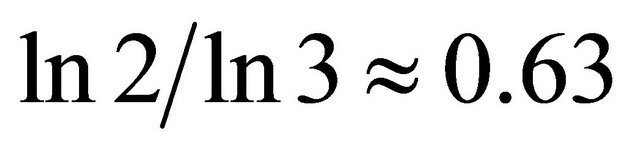 [1-4]. Noting that we have nothing left except uncountably many points of topological dimensions equal zero [1-4], a Hausdorff dimension equal 0.63 is relatively speaking quite substantial [2-4]. For the random Cantor set at hand, the situation is quite similar but instead of
[1-4]. Noting that we have nothing left except uncountably many points of topological dimensions equal zero [1-4], a Hausdorff dimension equal 0.63 is relatively speaking quite substantial [2-4]. For the random Cantor set at hand, the situation is quite similar but instead of 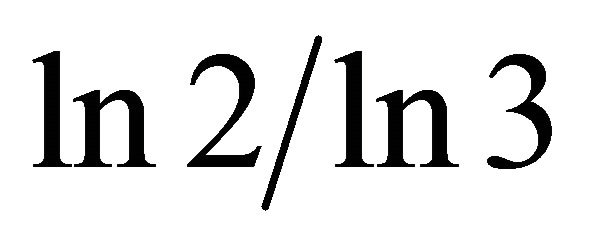 as a Hausdorff dimension we end up with the remarkable golden mean value
as a Hausdorff dimension we end up with the remarkable golden mean value
 as was shown some time ago by the two American mathematicians, Mauldin and Williams [5-7]. Considering now that for the original line segment, both the topological and the Hausdorff dimensions coincide and are equal to
as was shown some time ago by the two American mathematicians, Mauldin and Williams [5-7]. Considering now that for the original line segment, both the topological and the Hausdorff dimensions coincide and are equal to , then it follows that for the gaps left, representing by definition and construction, regions of No space and No time, we have a Hausdorff dimension equal to
, then it follows that for the gaps left, representing by definition and construction, regions of No space and No time, we have a Hausdorff dimension equal to  [3-6]. From these elementary considerations we will proceed in the next sections to derive exact energy expressions for ordinary energy and dark energy and show how the sum of these two energies constitute a novel derivation of Einstein’s famous energy expression E = mc2 [8].
[3-6]. From these elementary considerations we will proceed in the next sections to derive exact energy expressions for ordinary energy and dark energy and show how the sum of these two energies constitute a novel derivation of Einstein’s famous energy expression E = mc2 [8].
2. Topological-Geometrical Density Analysis
Let us analyze the two complementary Cantor sets introduced in Section 1. Thus we have the following two sets to consider [1,2,6,7]:
(a) An uncountable infinite number of Zero dimensional points with Zero measure [2,7] i.e. Zero length and a points set possessing a Hausdorff dimension equal to [3-7]
 (1)
(1)
(b) An infinite but countable number of gaps with a complementary Hausdorff dimension equal to [8-11]
 (2)
(2)
By contrast to the measure i.e. the length of the complementary set is still equal to .
.
Our next step is to lift both the  points set and the
points set and the  collection of gaps to Kaluza-Klein five dimensional spacetime [12,13]. Proceeding in this way we encounter two distinct situations:
collection of gaps to Kaluza-Klein five dimensional spacetime [12,13]. Proceeding in this way we encounter two distinct situations:
i) For  we calculate a quasi-Hausdorff hyper volume [8-11] by extending our familiar area and volume definition to formally five dimensions. That means we have a topological density
we calculate a quasi-Hausdorff hyper volume [8-11] by extending our familiar area and volume definition to formally five dimensions. That means we have a topological density
 (3)
(3)
for a Kaluza-Klein  spacetime [12,13]. Since the topological probability of finding a “Cantor point” in our set is
spacetime [12,13]. Since the topological probability of finding a “Cantor point” in our set is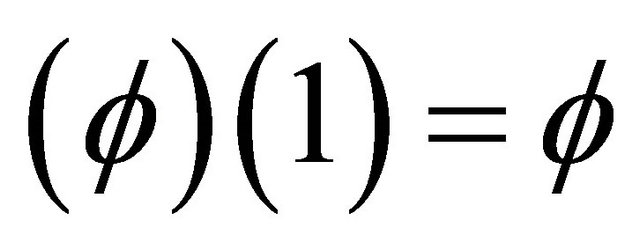 , then
, then 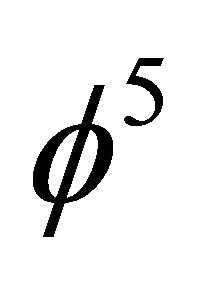 given by Equation (3) can be understood as an application of the intersection rule of sets or alternatively as the multiplication theorem of probabilistic events [2,6-8].
given by Equation (3) can be understood as an application of the intersection rule of sets or alternatively as the multiplication theorem of probabilistic events [2,6-8].
ii) For  on the other hand, we have a dual additive quasi-Hausdorff measure representing the total length of the circumference of a pentagon with the length of each side being equal to
on the other hand, we have a dual additive quasi-Hausdorff measure representing the total length of the circumference of a pentagon with the length of each side being equal to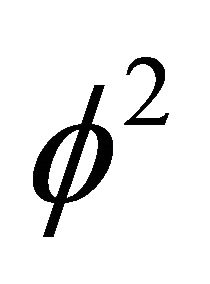 . In other words lifting additively the Hausdorff dimension of the complementary set i.e.
. In other words lifting additively the Hausdorff dimension of the complementary set i.e. 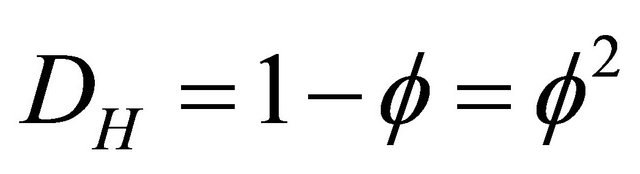 to
to  would give us a topological density equal to a quasi-hyper volume
would give us a topological density equal to a quasi-hyper volume
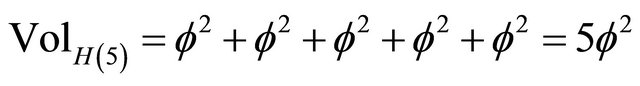 (4)
(4)
Similar to , the result given by Equation (4) may be interpreted as application of the addition rule of events of probability theory or equivalently as the union rule of sets [2,6-8]. In the Appendix we give more details of the above, in addition to instructive graphical illustrations (see Figures A1and B1).
, the result given by Equation (4) may be interpreted as application of the addition rule of events of probability theory or equivalently as the union rule of sets [2,6-8]. In the Appendix we give more details of the above, in addition to instructive graphical illustrations (see Figures A1and B1).
3. Adding Dynamics to Topology
Next we look at the magnitude of Newtonian kinetic energy
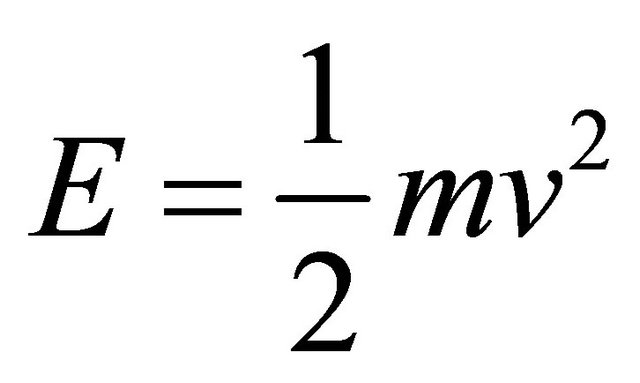 (5)
(5)
Inside 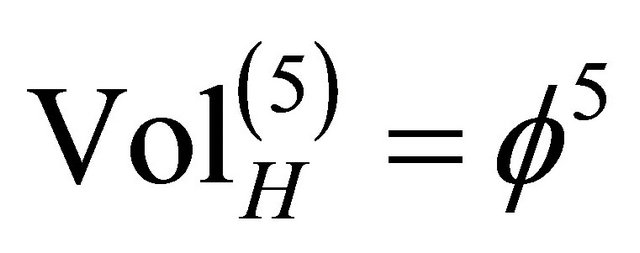 and
and 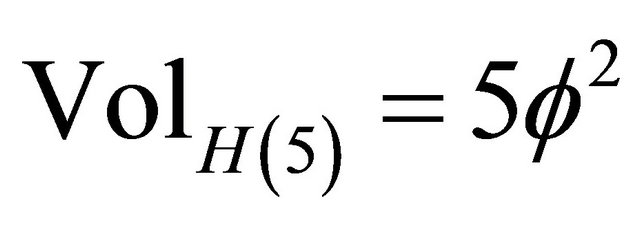 which represent a pure topological-geometrical density when
which represent a pure topological-geometrical density when  where m is mass, v is velocity and c is the speed of light [8,14] (see Appendix Part 3 and Part 4). In a similar manner to the above, we find two different types of energies:
where m is mass, v is velocity and c is the speed of light [8,14] (see Appendix Part 3 and Part 4). In a similar manner to the above, we find two different types of energies:
1) The energy associated with the geometrical or in fact topological density 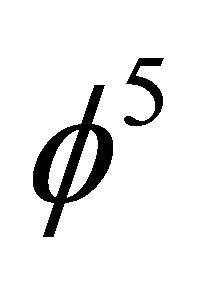 is obviously
is obviously
 (6)
(6)
Noting that  is equal to the celebrated Hardy probability for quantum entanglement [8,15] where
is equal to the celebrated Hardy probability for quantum entanglement [8,15] where is the Hausdorff dimension for the zero set fractal (i.e. a set of only Zero in it) modeling the quantum particle given by
is the Hausdorff dimension for the zero set fractal (i.e. a set of only Zero in it) modeling the quantum particle given by
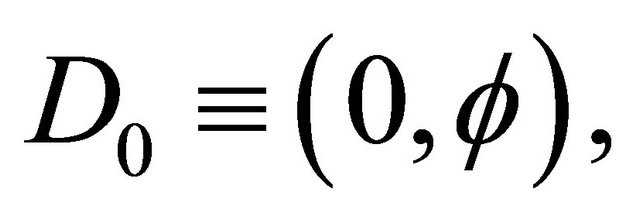 (7)
(7)
then we see that this is the ordinary energy of a quantum particle which will be denoted by[14]
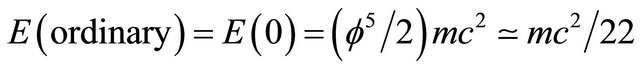 (8)
(8)
This energy density is only 4.5% of what Einstein’s relativity theory predicts classically and is thus equal to the energy density found from the WMAP measurement and Supernova cosmological data analysis [14,16] (For more detail see Appendix Figure A1).
2) By contrast for the energy density due to the density 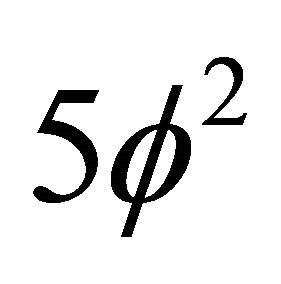 associated with Pentagonal surface or halo of the
associated with Pentagonal surface or halo of the  particle connected to a set with nothing in it i.e. the empty set
particle connected to a set with nothing in it i.e. the empty set
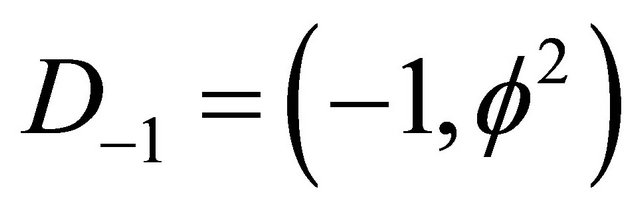 (9)
(9)
by which classical set theory starts, or the quantum wave in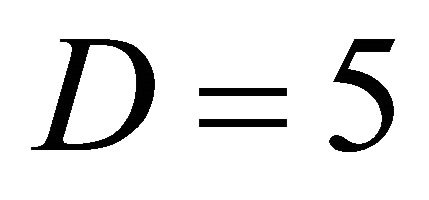 , we have
, we have 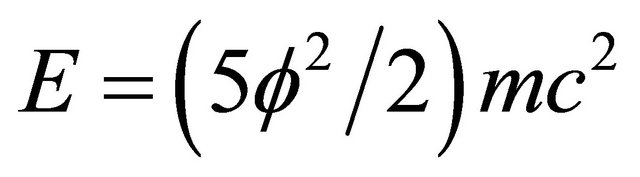 [5] (see Appendix Figure B1). It is easily shown that this is the value of the supposedly missing dark energy of the cosmos [14,16,17] and will therefore be denoted by
[5] (see Appendix Figure B1). It is easily shown that this is the value of the supposedly missing dark energy of the cosmos [14,16,17] and will therefore be denoted by
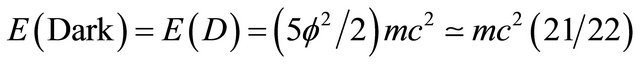 (10)
(10)
This energy obviously has a different sign to 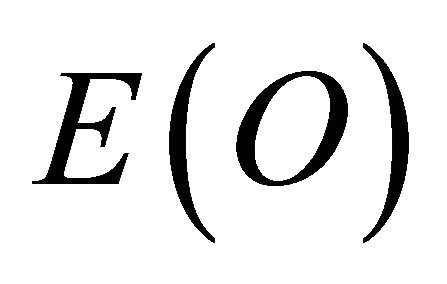 and therefore produces a form of antigravity force [16] which explains the increased rate of cosmic expansion observed in relatively recent accurate cosmological measurements [16] and attributes it to the negative anticlastic curvature of the compactified 22 bosonic dimensions of spacetime as distinct from the normal 4 large dimensions (i.e. three space and one time dimension fused together relativistically).
and therefore produces a form of antigravity force [16] which explains the increased rate of cosmic expansion observed in relatively recent accurate cosmological measurements [16] and attributes it to the negative anticlastic curvature of the compactified 22 bosonic dimensions of spacetime as distinct from the normal 4 large dimensions (i.e. three space and one time dimension fused together relativistically).
From the above we must conclude that when summing up  and
and  we will obtain E(Einstein) which is easily verified using elementary arithmetic based on the fact that
we will obtain E(Einstein) which is easily verified using elementary arithmetic based on the fact that 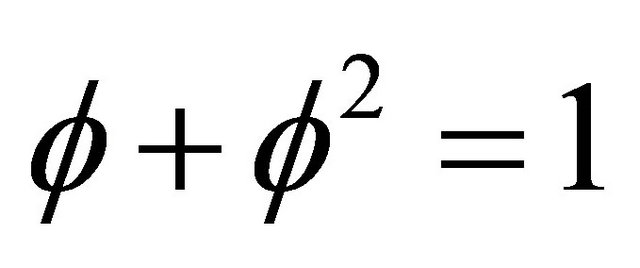 and
and 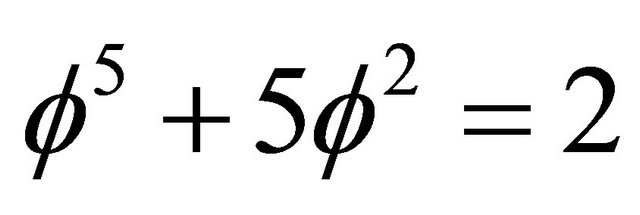 (see also Appendix Part 3 and Part 4 for more details). Thus we have the wonder which is no wonder namely that
(see also Appendix Part 3 and Part 4 for more details). Thus we have the wonder which is no wonder namely that
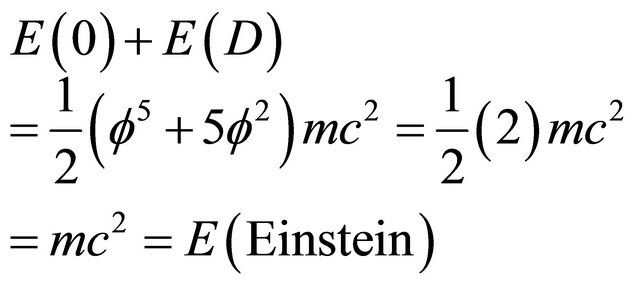 (11)
(11)
Equations (1) to (11) maybe regarded as a new insightful derivation of Einstein’s iconic equation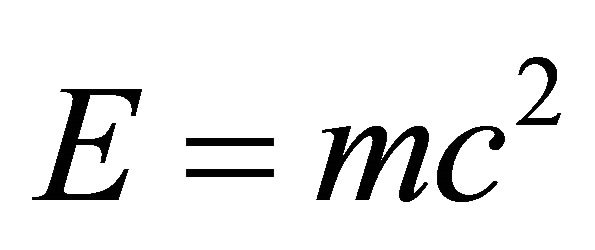 . More details of the above computation are given in the appendix where an alternative derivation using the theory of varying speed of light [18,19] is presented (see Appendix Part 5).
. More details of the above computation are given in the appendix where an alternative derivation using the theory of varying speed of light [18,19] is presented (see Appendix Part 5).
4. Discussion and Conclusion
Dark energy is the negative energy of the quantum surface or the outside of the quantum particle i.e. the quantum wave while ordinary energy is the energy of the inside core of the quantum wave which is the quantum particle (see Figures A1 and B1 as well as Part 3 and Part 4 of the Appendix). In Set Theoretical terminology [5], ordinary energy is the energy of the zero set while dark energy is the complementary energy of the empty set. An equivalent string theoretical explanation leading to the same conclusion is to consider dark energy to be the anticlastic curvature caused by the 22 compactified dimensions of the 26 dimensions of bosonic strings’ spacetime theory. The situation is thus just the opposite of a Faraday cage or a black hole where all vital quantities i.e. electric charge and entropy are proportional to the outside surface area and not to the inside core or volume (see Appendix Part 1 and Part 2).
Einstein’s energy is thus blind to any distinction between dark energy and ordinary energy density. However our present day apparatus feels the difference and can register only ordinary positive energy and that is the explanation for the result of the cosmological measurement, be it that only 4.5% of the energy predicted by the Theory of Relativity [16] is present or that the universe is pushed apart rather than being pulled together as we previously presumed and which new accurate measurements have now contradicted [14,16,17].
We note that because the Axiomatic structure of set theory and mathematical consistency could not be guaranteed without the introduction of the empty set as well as the zero set, then by the same token it follows that fundamental quantum physics and quantum gravity could not be consistent nor understood except by embracing the vital role of the particle-wave duality and its connection to the zero set-empty set duality. In a nutshell traditional physics does not recognize the empty set and equate it to an absolute nothingness. It is imperative to recognize that physics depends upon logical structure and it should never confuse the zero set with the empty set. It is equally imperative to confuse neither the zero set nor the empty set with insubstantial total nothingness.
One should not be entirely surprised that an empty set has a physical effect because a quantum Schrödinger wave which is merely a probability wave, devoid of ordinary matter and energy, also has a physical effect. It is an elementary fact of quantum physics discovered long ago by Max Born that the square of the probability wave function gives the probability of finding the spatial location of a quantum particle [6]. In a way dark energy discloses the mystery of the quantum wave function and vice versa. That may be a circulatory explanation or worse still tautology. However logical understanding is partially achieved by reducing the number of concepts. At a minimum this is what we have done and explained once more in details using Magueijo-Smolin Theory of Varying Speed of Light in the Appendix Part 5.
Appendix
Part 1

Figure A1. The zero set particle and the empty set wave.
Part 2

Figure B1. Wave-particle duality in five dimensions.
Part 3
(C) Quantum Relativity Energy by Generalizing Newton’s Kinetic Energy
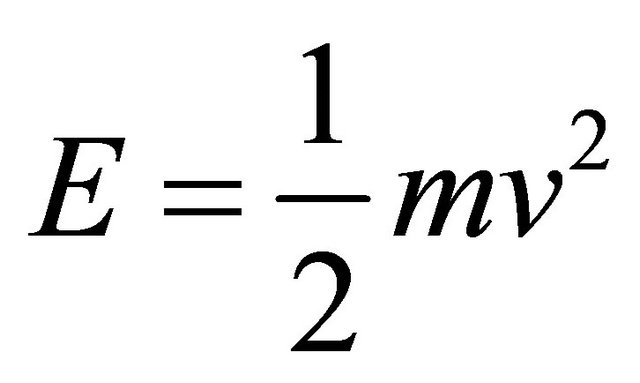 for
for  (A1)
(A1)
where E is the energy, m is the mass, v is the velocity and c is the speed of light is [14]:
(1) Energy of the quantum particle  Ordinary Energy
Ordinary Energy
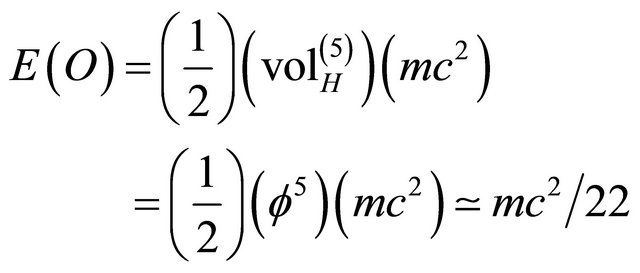 (A2)
(A2)
(2) Energy of the quantum wave  Dark (halo) energy
Dark (halo) energy
 (A3)
(A3)
(3) The sum of the ordinary energy E(O) of the quantum particle and the dark energy E(D) of the quantum wave is equal to Einstein’s energy [8,15]:
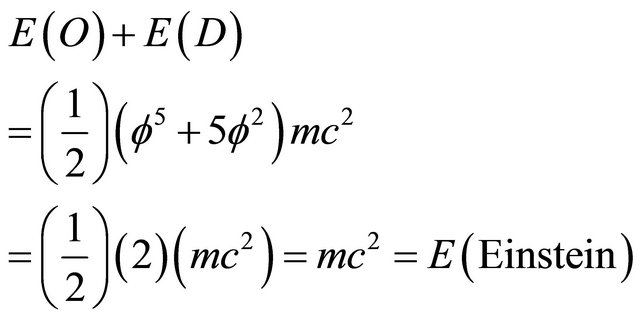 (A4)
(A4)
Conclusion:
Einstein’s 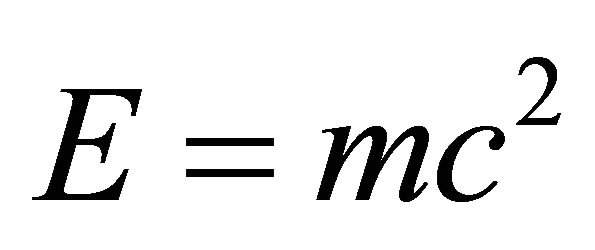 is blind to the distinction between ordinary energy and dark energy. The formula overlooks the fractality of the universe and that spacetime voids resemble the air in a gigantic cotton candy.
is blind to the distinction between ordinary energy and dark energy. The formula overlooks the fractality of the universe and that spacetime voids resemble the air in a gigantic cotton candy.
Part 4
(D) Intermediate Discussion:
A fractal 5D Kaluza-Klein spacetime [12,13] with
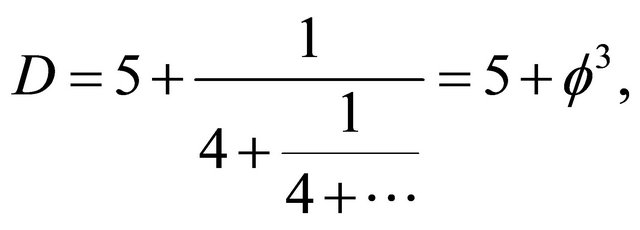 (A5)
(A5)
can be the explanation for the “missing” dark energy in the cosmos. Our measurement instruments register only the ordinary part of the following total energy given by:
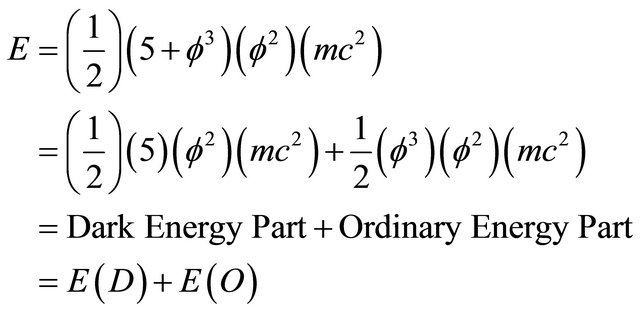 (A6)
(A6)
That means at present our technology makes it possible to measure directly only the ordinary energy given by:
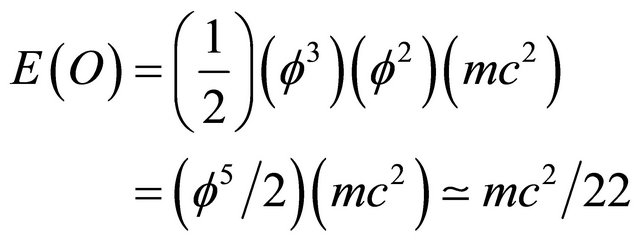 (A7)
(A7)
We have not yet developed instruments which can measure directly the negative dark energy of the vacuum i.e. the energy of the fractal spacetime voids which are devoid of space and time. This is not entirely surprising when we recall that dark energy is the energy of the quantum “probability” wave. Now we have maybe for the first time a deep physical and mathematical understanding of this otherwise puzzling “probability” wave [8].
Part 5
(E) Dark and Ordinary Energy from the Theory of Varying Speed of Light and T-Duality [18,19]
We start from Magueijo-Smolin varying speed of light quantum gravity energy formula [18,19]
 (A8)
(A8)
where 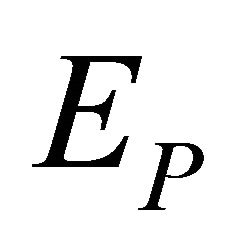 is the Planck energy. Subsequently we look at E when transformed using Witten’s T-duality [8]. That means
is the Planck energy. Subsequently we look at E when transformed using Witten’s T-duality [8]. That means
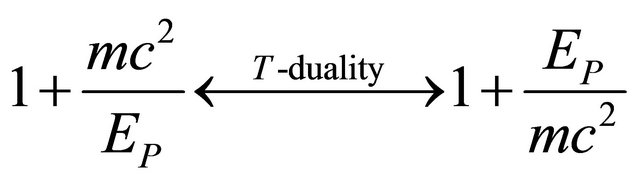 (A9)
(A9)
Here  is Hardy’s quantum entanglement probability [15] and m is Kaluza-Klein five dimensional mass
is Hardy’s quantum entanglement probability [15] and m is Kaluza-Klein five dimensional mass  while
while  is Sigalotti’s critical velocity [5-7]. Consequently we have two dual critical ratios
is Sigalotti’s critical velocity [5-7]. Consequently we have two dual critical ratios
 (A10)
(A10)
For 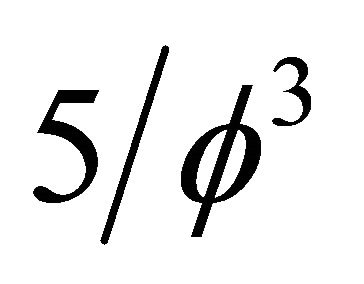 we find the quantum particle ordinary energy to be
we find the quantum particle ordinary energy to be 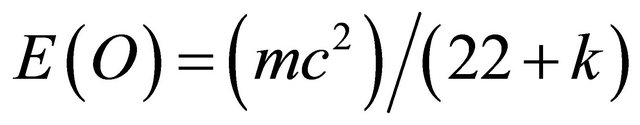 while for
while for 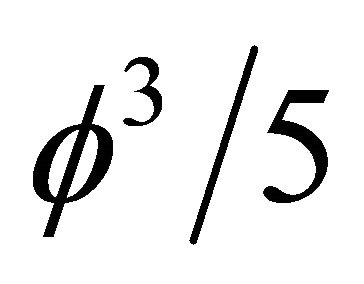 we find the so called dark energy of the quantum wave to be
we find the so called dark energy of the quantum wave to be
 . Adding
. Adding 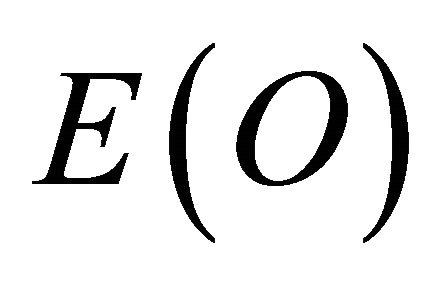 and
and
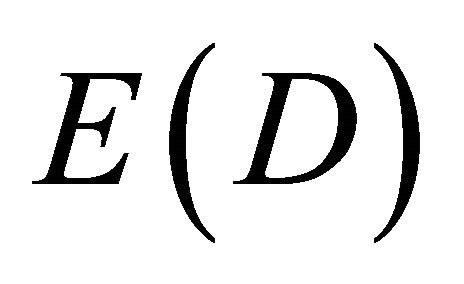 we find
we find 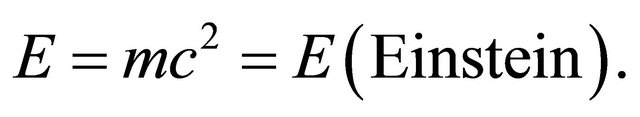
Letting the empty set  tend to a totally empty set
tend to a totally empty set 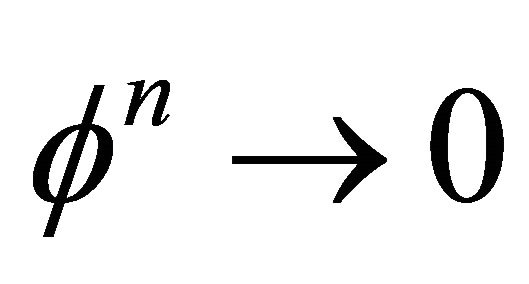 for
for  one finds
one finds 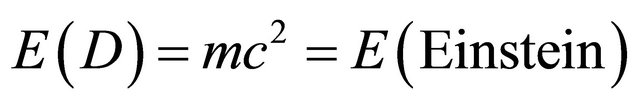 . On the other hand for
. On the other hand for
 we find the energy E to be that of a semiclassical Newtonian mechanics, namely
we find the energy E to be that of a semiclassical Newtonian mechanics, namely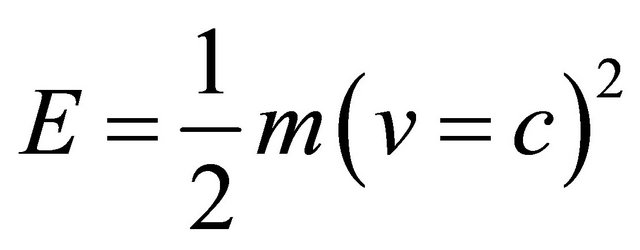 .
.
In a sense Einstein was not that far off when he described the quantum wave as a “Ghost” wave [8]. In fact the so-called missing dark energy of the cosmos belongs to the same esoteric ghostly entities. However far from being the work of sorcery, it is a rational magic emanating from the stringent Kantian “pure reasons” and logic of modern transfinite set theory [5-8]. Thus, our last and maybe most important conclusion is that we cannot detect or measure the dark energy of the quantum Hawking-Hartle wave of the universe because measurement leads to state vectors reduction and wave collapse. The only hope for detecting and utilizing dark energy in future reactors is the development of Nondemolition measurement instruments, if at all possible.