Appearance of Negative Differential Conductivity in Graphene Nanoribbons at High-Harmonics ()
1. Introduction
Graphene has attracted much attention since its discovery in 2004 by Geim and his team [1]. The great interest in studying graphene is driven by its unique band structure [2] and many unusual physical properties like electrical, thermal and mechanical properties [3]. Despite these, there have been difficulties in realizing graphene-based electronic devices, probably, the fact that the graphene sheet lacks band gap, edge defects, disorder, etc. However, various attempts have been made to introduce 2D graphene sheet, for the purpose of overcoming some of these challenges, into a 1D + quantization. This phenomenon results into graphene nanoribbon (GNR) which is assumed as an unrolled single-wall carbon nanotube (SWCNT).
Depending on the nature of the nanoribbon edges, one gets two symmetry groups; armchair graphene nanoribbon (aGNR) and zigzag graphene nanoribbon (zGNR). Armchair and zigzag GNRs show metallic or semicon-ducting electronic properties [4] depending on the number of dimer rows,  along transverse direction.
along transverse direction.  is related to the width of the nanoribbon as
is related to the width of the nanoribbon as 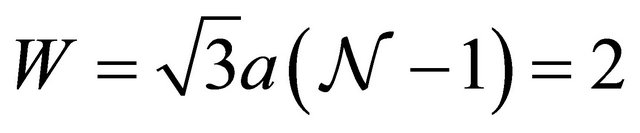 [5]. Electron dynamics of both ribbons have different properties, mostly due to the berry phase and pseudo spin [6]. Edge states have significant contribution to graphene properties, because in a nano-meter size ribbon, massless Dirac fermions can reach the edges within a femto-second before encountering any lattice effects, and avoiding electron-electron interaction, eletron-phonon interaction, etc.
[5]. Electron dynamics of both ribbons have different properties, mostly due to the berry phase and pseudo spin [6]. Edge states have significant contribution to graphene properties, because in a nano-meter size ribbon, massless Dirac fermions can reach the edges within a femto-second before encountering any lattice effects, and avoiding electron-electron interaction, eletron-phonon interaction, etc.
In this paper, we employ Boltzmann transport equation based on relaxation time approximation to study negative differential conductivity (NDC) in GNRs. In conventional semiconductor devices including semiconductor superlattices, an NDC behavior is known to offer great potential for high frequency applications as Bloch oscillators, frequency multipliers, and fast switching devices. For this reason, the NDC effect has been greatly explored and discussed in several graphene nanostructures, particularly in [7]. NDC can also be observed in other graphene allotropes; carbon nanotubes (CNT) [8]. The unique energy spectrum of holes and electrons in GNRs, especially its narrow gap nature leads to nontrivial features such as NDC in the THz regime [7].
The rest of this paper is organized as follows; In Section 2, we derived the electronic current density of aGNR and zGNR and imposed certain conditions to reduce the equations to forms appropriate for our model. The results obtained in Section 3 are discussed in great details in Section 4. The paper finally concludes in Section 5 where some recommendations for future applications are made.
2. The Theory
Following the approach of refs, [8,9] for SWCNT and semiconductor superlattices, we consider an undoped GNR (both zigzag and armchair) exposed simultaneously to  electric field
electric field
 (1)
(1)
which is seen as a superposition of n harmonic waves polarized along one direction with angular frequency. The phase difference between the  th and
th and  th component being
th component being  is arbitrary,
is arbitrary,  is an integer.
is an integer.  are the field amplitudes. We require that
are the field amplitudes. We require that  . This will correspond to the DC component of the applied field. The dynamics of free
. This will correspond to the DC component of the applied field. The dynamics of free  -electrons in graphene can be describe by the time-dependent Boltzmann transport equation (BTE) based on relaxation time approximation in zero magnetic field as
-electrons in graphene can be describe by the time-dependent Boltzmann transport equation (BTE) based on relaxation time approximation in zero magnetic field as
 (2)
(2)
We also assume a spatial uniform graphene nanoribbon. Again, the inverse of the relaxation time  is momentum independent. In Equation (1),
is momentum independent. In Equation (1),  and
and  are the equilibrium and non-equilibrium Fermi electron distribution functions, respectively.
are the equilibrium and non-equilibrium Fermi electron distribution functions, respectively.  is the electronic charge,
is the electronic charge, 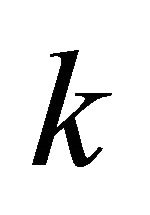 is the electron wave vector and
is the electron wave vector and  is the reduced plank constant. In the following section, we will calculate electronic current density for GNRs.
is the reduced plank constant. In the following section, we will calculate electronic current density for GNRs.
2.1. Armchair and Zigzag Nanoribbon Band Structures
The energy band structure of aGNR and zGNR is characterized by three parameters; band index , phase
, phase  and wave vector
and wave vector  [5,6]. For aGNR,
[5,6]. For aGNR,
 (3)
(3)
and for zGNR,
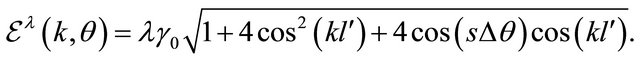 (4)
(4)
where  with (+) for conduction band and (−) for valence band.
with (+) for conduction band and (−) for valence band. 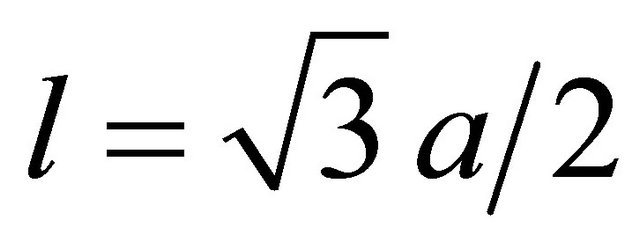 and
and ,
,  is the lattice spacing which has numerical value of 0.246 nm,
is the lattice spacing which has numerical value of 0.246 nm,  is the overlap integral and
is the overlap integral and  is the phase perpendicular to the quasi-momentum
is the phase perpendicular to the quasi-momentum . The 1 BZ of aGNR is bounded by
. The 1 BZ of aGNR is bounded by  and the zGNR is
and the zGNR is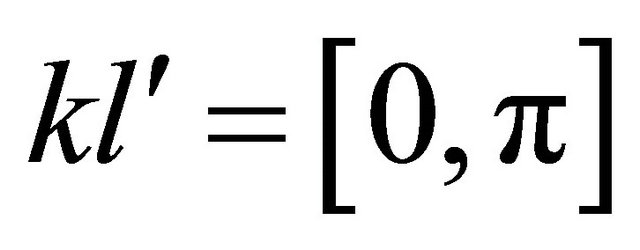 .
.  is parallel to the edge and has translational symmetry along this direction. For aGNR, the transverse wave vector (phase) is quantized according to the rule [6]
is parallel to the edge and has translational symmetry along this direction. For aGNR, the transverse wave vector (phase) is quantized according to the rule [6]  with
with 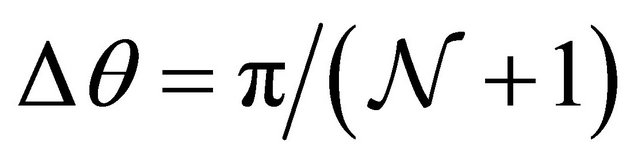 and
and  . Unlike aGNR, the nature of transverse wave vector quantization is complicated in zGNR, depending on both
. Unlike aGNR, the nature of transverse wave vector quantization is complicated in zGNR, depending on both 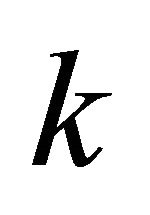 and
and  as
as . However, for simplicity we assume
. However, for simplicity we assume  is constant, say
is constant, say , so that
, so that  . Except this little subtlety for zGNRs, all that will be discussed in the following for aGNR are equally applied to the zGNR.
. Except this little subtlety for zGNRs, all that will be discussed in the following for aGNR are equally applied to the zGNR.
Now, we employed the translational invariance of graphene ribbon in the reciprocal space and expand in Fourier series functions  and
and  along the edge having periodicity in
along the edge having periodicity in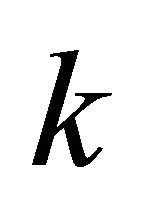 . i.e.,
. i.e.,
 (5)
(5)
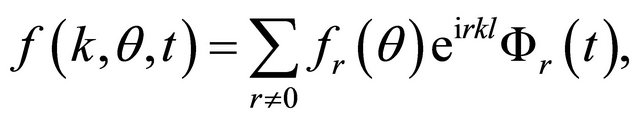 (6)
(6)
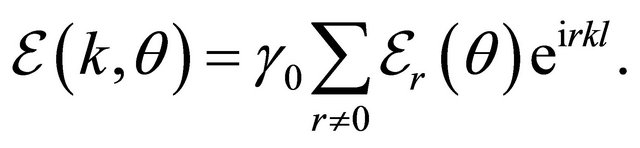 (7)
(7)
The Fourier coefficient  is expressed as
is expressed as
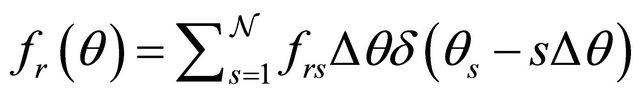 with
with
 (8)
(8)
and
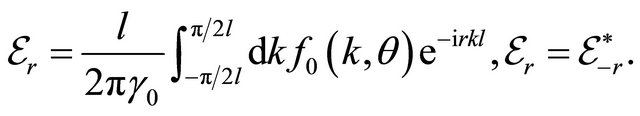 (9)
(9)
In (6),  counts the number of dimers
counts the number of dimers  in the GNRs. The factor
in the GNRs. The factor  in the equation is a central point in this paper and so has to be determined.
in the equation is a central point in this paper and so has to be determined.  is an integer and not equal to zero. We consider a classical limit in which energy levels could be excited due to thermal fluctuations, i.e.
is an integer and not equal to zero. We consider a classical limit in which energy levels could be excited due to thermal fluctuations, i.e. . This condition is also necessary for large enough field, so that charge carriers can escape low energy scattering [10]. The energy level spacing
. This condition is also necessary for large enough field, so that charge carriers can escape low energy scattering [10]. The energy level spacing ,
,  is the charging energy,
is the charging energy,  is Boltzmann constant,
is Boltzmann constant,  is lattice temperature and
is lattice temperature and  is the graphene nonoribbon width. In what follows, we will compute
is the graphene nonoribbon width. In what follows, we will compute  To do this, (5), (6) and (7) are substituted in (1) following the simplification scheme
To do this, (5), (6) and (7) are substituted in (1) following the simplification scheme  and
and . We obtained
. We obtained
 (10)
(10)
where 
2.2. Sheet Current Density
The sheet current density of graphene can be determined from the relation
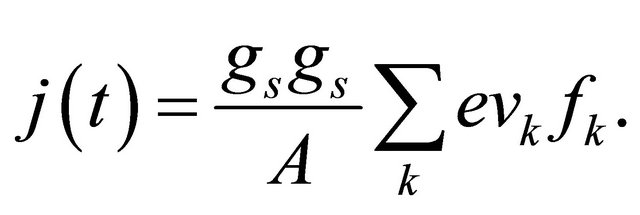 (11)
(11)
the sheet area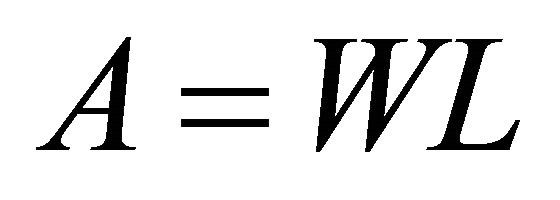 .
. ,
, 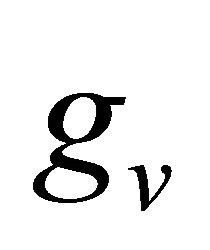 are the spin and valley degeneracies, respectively. The current density can also be written as
are the spin and valley degeneracies, respectively. The current density can also be written as
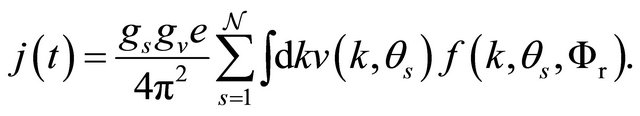 (12)
(12)
the velocity of Dirac fermions in graphene is defined as . In terms of the Fourier coefficients,
. In terms of the Fourier coefficients,
 (13)
(13)
Giving
 (14)
(14)
with
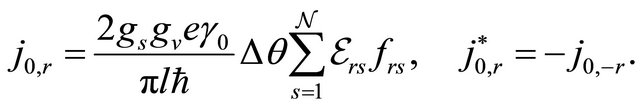
Note the  dependence of
dependence of ,
,  and the summation over the index in (10). Using the formalism by Litvinov and Manasson [9]. Equation (14) can be put in a Taylor-like expansion in terms of
and the summation over the index in (10). Using the formalism by Litvinov and Manasson [9]. Equation (14) can be put in a Taylor-like expansion in terms of . i.e.,
. i.e.,
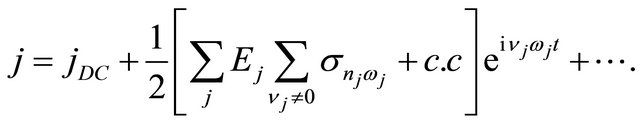 (15)
(15)
where
 (16)
(16)
is the differential  current density (for
current density (for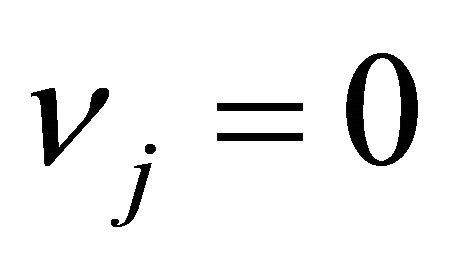 ), and
), and
 (17)
(17)
is the large-signal dynamic nonlinear conductivity at  harmonic with drive frequency
harmonic with drive frequency .
.
3. Negative Differential Conductivity
3.1. Pure DC Limit
To see immediately that (16) demonstrates NDC, we consider a pure DC limit where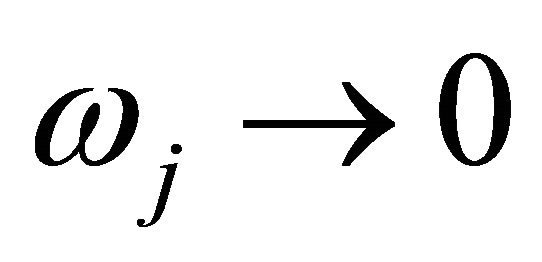 . The Bessel functions except the
. The Bessel functions except the  term will vanish. The real part of the differential conductivity
term will vanish. The real part of the differential conductivity 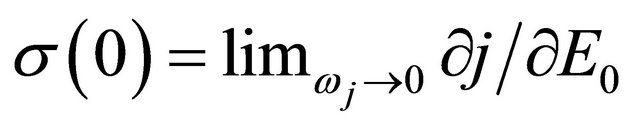 become
become
 (18)
(18)
So that if  the differential conductivity is negative and NDC is manifest in GNRs. Electron dynamics may be come more complicated in the presence of high-frequency components in addition to the static electric fields. High negative differential conductivity thus may result in GNRs if an external drive force is applied.
the differential conductivity is negative and NDC is manifest in GNRs. Electron dynamics may be come more complicated in the presence of high-frequency components in addition to the static electric fields. High negative differential conductivity thus may result in GNRs if an external drive force is applied.
3.2. Monoharmonics
If one component of the AC field in (2) is applied, then  and (16) simplifies to
and (16) simplifies to
 (19)
(19)
after dropping the subscript on  Here, it not clear immediately how NDC can be seen. To observe the phenomenon, we plot
Here, it not clear immediately how NDC can be seen. To observe the phenomenon, we plot  with
with 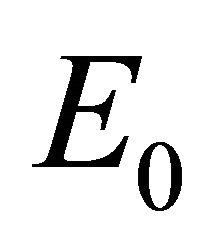 for
for  as shown in Figure 1 (top) for armchair ribbon and in Figure 1 (buttom) for zigzag ribbon,
as shown in Figure 1 (top) for armchair ribbon and in Figure 1 (buttom) for zigzag ribbon,
The effect of NDC is strong in zigzag graphene than in armchair graphene. Especially, in the limit of high harmonic field, NDC is greatly suppressed in aGNR.
3.3. Biharmonics
In practical situations, one can also allow graphene nanoribbon subject to two AC field components. In that case, we let  in our general formalism in Section 2. Equation (15) takes the form
in our general formalism in Section 2. Equation (15) takes the form
 (20)
(20)
and from which (17) follows. We have eliminated the time dependence by averaging over the period of the fields to find the time-independent current . In the left hand side, we replaced
. In the left hand side, we replaced , and in the right hand side a delta function emerges which ensures that
, and in the right hand side a delta function emerges which ensures that . If
. If , then one must put
, then one must put  and
and  so that
so that . However, we shall generalize this to a case of commensurate frequencies. We exemplified the case by a biharmonic having frequencies which can be periodic
. However, we shall generalize this to a case of commensurate frequencies. We exemplified the case by a biharmonic having frequencies which can be periodic  or non-periodic,
or non-periodic,  with
with 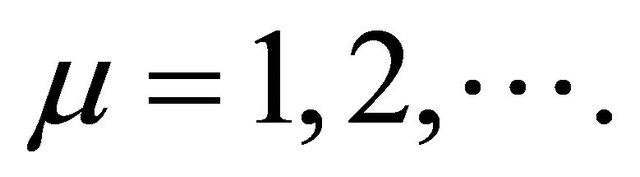 These two cases were studied in [11,12] for semiconductor superlattices. Simplifying further, we linearize with respect to one of the field amplitudes (say,
These two cases were studied in [11,12] for semiconductor superlattices. Simplifying further, we linearize with respect to one of the field amplitudes (say, ). For a week field,
). For a week field,  and
and , which allows us to take
, which allows us to take . Finally, the AC current density becomes
. Finally, the AC current density becomes
 (21)
(21)
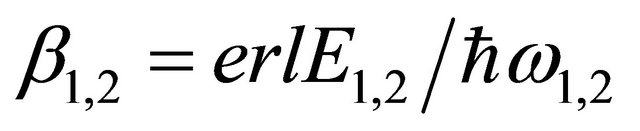 . Equation (21) reduces to the monoharmonic case when
. Equation (21) reduces to the monoharmonic case when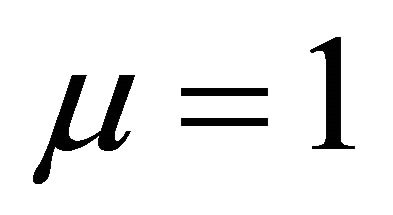 .
.
The nature of the NDC is observed for a simultaneously varying harmonic field and phase difference in a three dimensional plot shown in Figure 2.
4. Discussion and Conclusions
In Figure 1 normalized current density  is plotted against reduced static electric field
is plotted against reduced static electric field  for aGNR (left) and zGNR (right) for an applied
for aGNR (left) and zGNR (right) for an applied  field. At low fields up to
field. At low fields up to , the quantum derivative of the
, the quantum derivative of the  characteristic yields a positive slope. A negative slope results for
characteristic yields a positive slope. A negative slope results for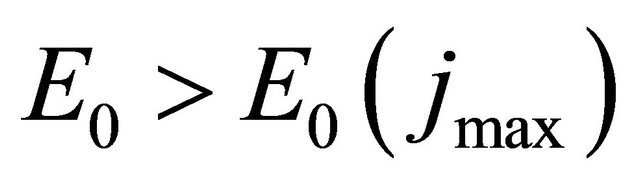 . In the whole region,
. In the whole region,  graphene nanoribbon device will operate under Negative Differential Conductivity (NDC). A consequence of NDC in GNR is a formation of electric field domains that impedes a continuous motion of electrons generated by the external electric field and thus blocks high frequency oscillations in the nanoribbon. NDC disappears quite faster in aGNR as
graphene nanoribbon device will operate under Negative Differential Conductivity (NDC). A consequence of NDC in GNR is a formation of electric field domains that impedes a continuous motion of electrons generated by the external electric field and thus blocks high frequency oscillations in the nanoribbon. NDC disappears quite faster in aGNR as  compared to zGNR which is more rubust at this limit.
compared to zGNR which is more rubust at this limit.
The curves in Figure 3 demonstrate NDC phenomenon. They are obtained at wave mixing of two commensurate frequencies,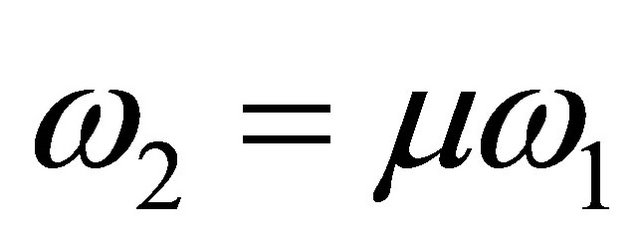 . Figure 3 (left),
. Figure 3 (left),  and Figure 3 (right),
and Figure 3 (right),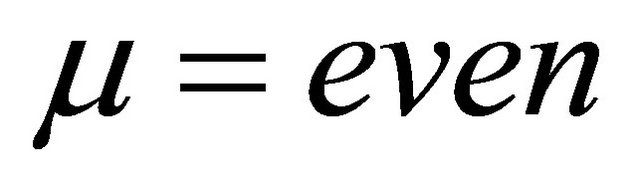 . The onset of NDC in oddharmonics occurs around
. The onset of NDC in oddharmonics occurs around  and in even-harmonics it starts at
and in even-harmonics it starts at . In both cases, as in the previous NDC graphs,
. In both cases, as in the previous NDC graphs,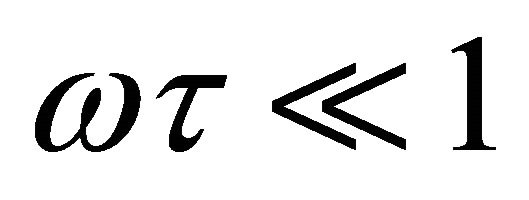 .
.
The combined effect of phase shift , between two
, between two 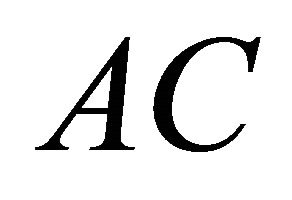 fields and amplitude on NDC is depicted in Figure 2. There are three peaks at low bias fields at points
fields and amplitude on NDC is depicted in Figure 2. There are three peaks at low bias fields at points ,
, 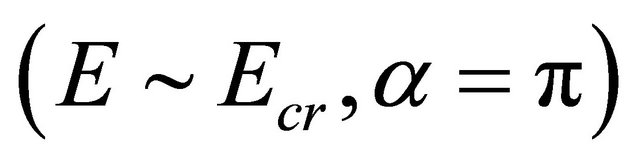 and
and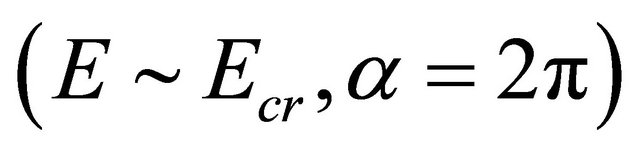 . It is not very clear what these crests and troughs mean, they might be associated with field domains along one direction (for
. It is not very clear what these crests and troughs mean, they might be associated with field domains along one direction (for ) and others along the opposite direction (for
) and others along the opposite direction (for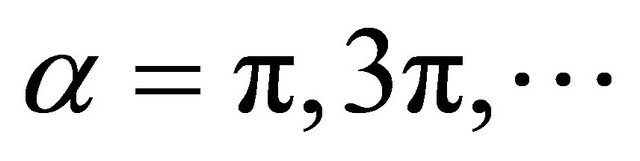 ) and vice-versa. This means that electron velocity is higher in the domain with the same polarization along the electron direction and lower in the domain with opposite polarization.
) and vice-versa. This means that electron velocity is higher in the domain with the same polarization along the electron direction and lower in the domain with opposite polarization.
In conclusion, we have demonstrated that graphene nanoribbons exhibit NDC regions in its  characteristics at low bias field when
characteristics at low bias field when . NDC is observed either in the presence of bias field alone or by superimPosing AC fields on the bias field. For one AC field component, NDC occurs around
. NDC is observed either in the presence of bias field alone or by superimPosing AC fields on the bias field. For one AC field component, NDC occurs around . When two AC fields at commensurate frequencies are applied, highharmonic NDC emerge for both even and odd harmonics at rather very low frequencies
. When two AC fields at commensurate frequencies are applied, highharmonic NDC emerge for both even and odd harmonics at rather very low frequencies . The evenseries gives pronounced high-harmonic NDC than the odd-series. The presence of high-harmonic NDC means that it is possible for high-frequency generation in graphene nanoribbons when electric field domains are suppressed at high enough applied frequencies
. The evenseries gives pronounced high-harmonic NDC than the odd-series. The presence of high-harmonic NDC means that it is possible for high-frequency generation in graphene nanoribbons when electric field domains are suppressed at high enough applied frequencies  and
and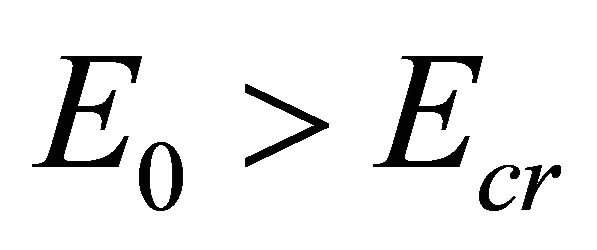 . We therefore suggest this approach for the
. We therefore suggest this approach for the

Figure 2. Negative differential conductivity of aGNR due to applied static field amplitude, 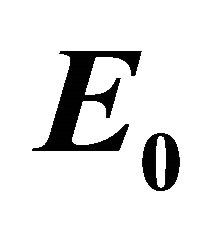 and phase shift,
and phase shift,  between two AC fields.
between two AC fields.
study of terahertz generation in graphene.