Thermal, infrared spectroscopy and molecular modeling characterization of bone: An insight in the apatite-collagen type I interaction ()
1. INTRODUCTION
Biominerals such as teeth, shells, eggshells and bones are subject of a significant research because of their characteristic structural arrangements and unique mechanical and physicochemical properties [1-7]. The determination of their structure at the nanoscale is a critical step in understanding their properties and formation mechanismsand to design new biomimetic solids [5,8-10]. Among these hard biostructures, bone has two main components:
the carbonate apatite (≈70%), and the collagen type I protein (≈30%) [9]. The structure of bone at the nanoscale as the organic-inorganic interactions, are not yet completely understood, and this information might be essential for the synthesis of new composite materials for biocompatible ceramics or other nanostructured biomimetic materials [1,4,6,9]. The extraordinary hierarchical structure of bone originates different interactions between the crystalline apatite phase, collagen macromolecules, and cells producing a complex structure at different scales [4]. Crystal size, morphology and properties of the mineral component might be originated from a collagen template [9,11], making up a genetically-controlled crystallization [12]. Some authors recently determined crystal sizes approximately of 5 nm thick, 70 nm wide and several hundred nm long [13]. It is possible that the biological process exploits the existence of unique repetitive motifs in the organic molecule [14], to control the fine structures of the inorganic solids [15,16]. [15-17] the exploitation of molecular recognition at the organicinorganic interface offers the opportunity to systematically use specific macromolecules [8,16] for binding of previously selected crystalline faces, stimulating or inchibiting the crystal growth in a predictable manner, as in biological hard tissues [7,11]. Significant studies on hard tissues were performed to know the thermal changes through different temperatures [18-21]. In such cases, the thermal transitions below 120˚C offered information about the non covalent changes in collagen [19]. Studies at higher temperatures (150˚C up to ca. 600˚C) used successfully differential scanning calorimetry (DSC) together with X-rays in bones [18,22,23] to characterize the thermal behavior of the biomineral [20,24]. For instance, the ΔH values, obtained by DSC, of the collagen from Achilles tendon and organic extracts from bone are not very different, although the characteristic maximum reaction peak (Tmax) of collagen (ca. 550˚C) shifts towards lower temperatures (365˚C), apparently due to interactions with apatite nanocrystals [18]. This assumption is based on the fact that apatite does not exhibit such shifts at those temperatures, e.g. nor in the bone-extracted inorganic material neither in the synthetic apatite samples [25].
Nonetheless, very scarce information on thermal analysis in biominerals remains and whether or not the role of the chemical differences of the surface of apatite nanocrystals exerts changes in the interacting collagen [25,26]. Herein, we attempt to give a further explanation of the nature of the thermal behavior of bone and the interactions between the model of the collagen type I and bone apatite by using Fourier transform infrared (FTIR) spectroscopy, DSC and molecular modeling.
2. MATERIALS AND METHODS
2.1. Materials
Bones used as controls in anthropological research [27,28] were supplied from the contemporary material from the Archaeometry laboratory at the Anthropological Research Institute at National Autonomous University of Mexico. Healthy young human adult radium (bone) was used in the experiments with no visible signs of illness. The pieces were cut and washed by gentle shaking with distilled water in an agate mortar for 1 h. The water was removed and substituted by 96% ethanol, and again the samples were washed by shaking during 5 days; the ethanol was changed every 3 hours [18,22]. The ethanol removes the lipids and other fat components of the collagen matrix. After rinsing, the samples were milled in the agate mortar and sieved to a 325 mesh. The organic content was obtained by boiling the powdered bone samples in distilled water for 1 h and evaporated by desiccation.
Commercial collagen type I extracted from bovine Achilles tendon (Sigma-Aldrich C-9879) was analyzed by DSC as control samples.
2.2. Experimental
FTIR analyses were carried out using a Nicolet 680 spectrophotometer. Commercial Sigma Collagen, extracted bone collagen, and bone samples were mixed with crystalline KBr powder (1:100 ratio) and compressed into pellets and scanned with a resolution of 4 cm−1 over 64 scans.
DSC measurements were performed on a Thermal Analysis System 9900, Du Pont 910 (DSC module). The heating was constant at a rate of 10˚C/min, in air atmosphere. The samples (1.0 mg for collagen and 2.0 mg for bone samples) were placed in aluminum pans [18].
SEM imaging for structural properties of the bones were studied using a scanning electron microscope (JSM-6300, Japan). Samples were coated with a thin film of carbon and then examined with an accelerating voltage of 15 kV with an Energy-dispersive X-ray spectroscopy (EDX) facility (Noran Vantage, USA). Samples were exposed to the electron beam for 30 seconds acquiring secondary electrons for the EDX spectra and images.
2.3. Molecular Modeling
Fragments of hydroxyapatite surface were constructed using ATOMS Version 6.0 (by Shape Software) for Windows, by extending and editing the unit cell. The resulting surface fragments represent (100) and (001) crystal planes and have an approximate size of 38 × 32 and 32 × 27 Å, respectively. For the modeling, we used the (100) plane and two (001) models, with phosphate and calcium-rich sides; they are shown in Figure 1.
MM+ molecular mechanics implemented in HyperChem Version 7.1 package [29] was used. As a collagenlike model, we used the fragment Gly-L-Pro-L-HypGly-L-Pro-L-Hyp-Gly-L-Pro-L-Hyp nonapeptide with zwitterionic terminations and helical structure. The peptide model was placed in the working space close to the apatite surface models (approximately over its center, at ca. 5 Å distance). By selecting (Selection Tool) the former and leaving the latter deselected, the surface fragment was frozen (as the simplest approach to simulate a crystal plane) [30], and only the peptide geometry was optimized. Geometry optimization was performed with the Polak-Ribiere conjugate gradient algorithm and a root mean square (RMS) gradient of 0.01 kcal Å−1×mol−1. To find different possible conformations and their corresponding local minima, we tested different starting orientations of the peptide with respect to the surfaces, as well as molecular dynamics annealing (step size of 0.001 ps; run time of up to 10,000 ps; simulation temperature of 300 K).
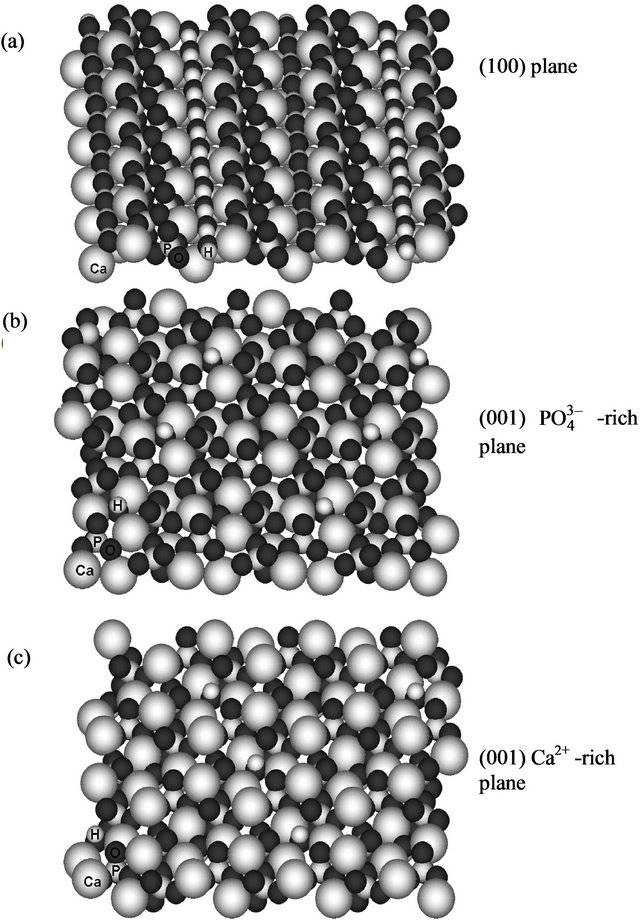
Figure 1. Surface fragments of hydroxyapatite used for MM+ molecular mechanics modeling: (a) (100) model; (b, c) (001) models, with phosphate (b) and calcium-rich sides (c). Atomic symbols are shown for several atoms at the bottom left.
3. RESULTS
3.1. FTIR Spectra
When analyzing FTIR spectra of the samples, we focused on variations in the signals related to amide bands [31-33]. The FTIR spectra of bone exhibit the bands of peptides (“amide I” at ca. 1650 cm−1 and “amide II” at ca. 1550 cm−1, in the segmented box) and apatite (Figure 2) [34]. For comparison, the FTIR spectra of the collagens purchased from Sigma, the extracted from the bone and the bone are presented in Figure 2. The band at 3400 cm−1 from secondary amines, in the extracted collagen from bone tissue shows a decrease in its intensity, probably due to the elimination of amines from non-collagen molecules and elimination of apatite, always containing adsorbed water and molecules [20,33,35].
Changes are seen in the peak corresponding to “amide I” C=O stretching vibrations [32] (A I in Figure 2, ≈1650 cm−1), what might be involved in the macromolecular interactions with the apatite phase. In the bone sample, Sigma and extracted collagen samples, “amide I” and “amide II” (≈1550 cm−1 [32]) signals exhibit different intensities compared to the FTIR bone spectrum too. Noticeable is that in the FTIR spectra of the whole bone tissue (Figure 2), the “amide II” band presents a higher intensity compared to those from the extracted collagens (dashed line inset in Figure 2). The reason, is likely the double bond character of peptide bond [36] that might change the distribution of its dipole moment of the helix when the collagen type I interacts with the nanocrystal
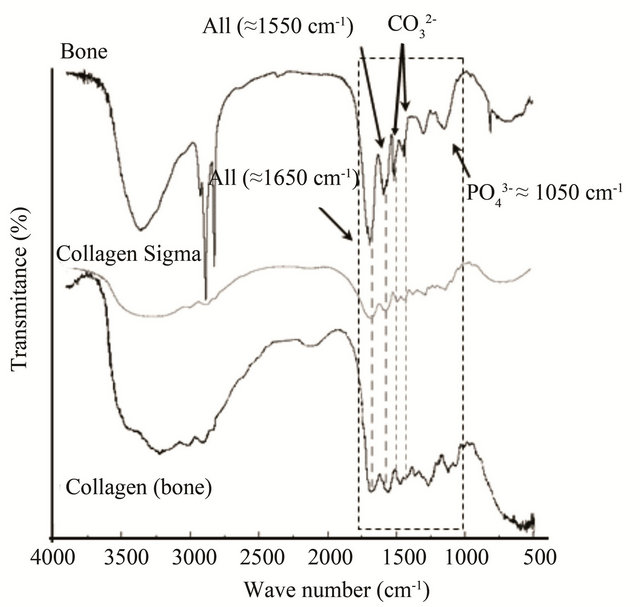
Figure 2. FTIR spectrum of healthy bone sample between 4000 and 500 cm−1. Some of the bands corresponding to the apatite (P-O at 1050 cm−1, and for carbonate group 1420 and 1470 cm−1) and the collagen “amide I” and “amide II” (“A I” and “A II” respectively) are shown.
[37]. Indeed the amide region is dependent on cross-links to the mineral [38]. The chemical and structural docking between the chemical groups in the peptide bond makes difficult to interpret the changes in the amide I and amide II bands.
3.2. Thermal Analysis
Figure 3 shows typical DSC curves for bone and collagen samples, these curves are consistent with other studies [18,21]. The single endothermic peak at 50˚C - 90˚C is probably due to the dehydration process, water molecules are present on the sample surfaces, as well as the macromolecular denaturalization and conformational changes or other different processes in collagen type I macromolecule. In bone sample, it is possible to observe an exothermic peak with a Tmax around 345˚C with a right shoulder at 425˚C. These signals comprising the range from 220˚C to 530˚C, represent complex processes of collagen degradation and combustion [18,20,23].
The thermal analysis of the human bone sample shows mainly two thermal transitions near 350 and 450˚C; Sigma collagen shows three exothermic transitions, namely at 185˚C (small but sharp), ca. 300˚C (diffuse) and 480˚C (main). The extracted collagen from bone exhibits three transitions at ca. 270˚C (diffuse), 455˚C (shoulder) and 500˚C (main).
3.3. Scanning Electron Microscopy
The investigation of the surface morphology of bone
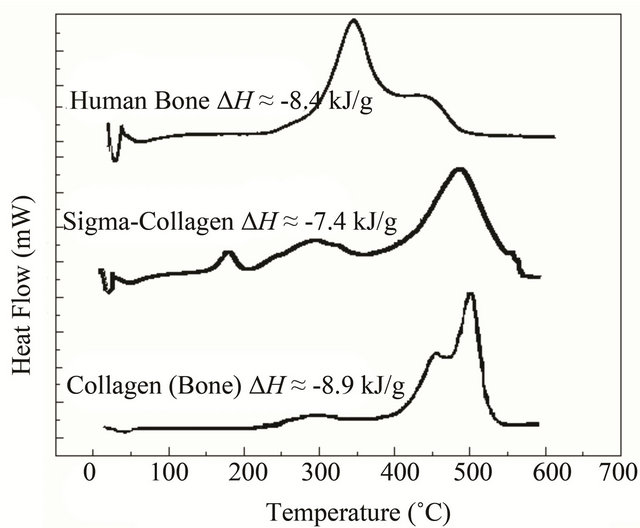
Figure 3. DSC comparison of thermal transitions from adult human bone, Sigma collagen and collagen extracted from bone. The exothermic transition represents the degradation and combustion process from 200˚C to 550˚C. The upper DSC shows a Tmax at 345 and a right shoulder at about ≈425˚C. The maximum of Sigma collagen is at temperatures lower than 550˚C. In the extracted collagen the peak of maximum thermal flow is at about 525˚C and it has on the left side a shoulder at about 465˚C. DH values [18] suggest that combustion is the same molecule.
using scanning electron microscope gave more details about the state of the surface (Figure 4), showing a very smooth surface in the control samples. Heating the samples the surface was coarse and some pittings were noticed. The deterioration was clearer the higher the temperature (Figure 4(d)), with some cracks. Destruction of the surface was coarse and the equality in the surface could be recognized in the control (Figure 4(a)) but not at higher temperatures in the micrograph Figures 4(b)-(d). After EDS analysis at different hours of thermal treatment the elemental analysis did not show clear changes in elemental content (Table 1, Figure 4(e)), although the destruction increased and the surface flattening was absent in most of the surface at the highest temperature.
This EDS analysis shows effectively the persistence of the inorganic material confirming that the reactions in the DSC experiments correspond to collagen type I (Table 1, Figure 4). EDS shows the stability of the apatite through the different temperatures [39].
3.4. Molecular Modeling
The fragments of hydroxyapatite surfaces were constructed by matching and editing the crystal face structure. For modeling, we used the (100) plane and two (001) models with phosphate and calcium-rich sides (shown in Figure 1). The final structures (Figure 5) obtained by geometry optimization reflected both the geometric correspondence of the collagen models with the surface fragments and the charge interactions. In this way, the order of affinity of the collagen type I model to hydroxyapatite surfaces is as follows: 4.31 kcal/mol (100) < 0.04 kcal/mol (001) phosphate-rich < 5.98 kcal/mol (001) calcium-rich. In our molecular model the (001) plane has more affinity to the simulated macromolecule, perhaps promoting a preferential growth in the (001) axis. The affinity is apparently favored by the interactions of collagen with the ,
,  tetrahedral groups as
tetrahedral groups as
Table 1. Elemental content of bone by weight after 30 minutes of thermal treatment.

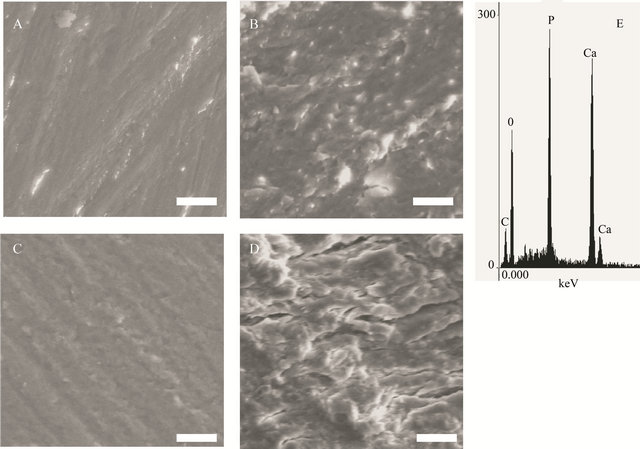
Figure 4. Scanning electron micrographs illustrate the change in the surface of bone, after exposure to different temperatures. (a) control, (b) 340˚C, (c) 500˚C, (d) 530˚C and (e) (scale bar 10 mm). Typical EDS analysis from the sample treated at 530˚C.
substantiated experimentally [40] and with the divalent ions of Ca2+ in this plane. We assume that the number of organic-inorganic contacts, the distance among the groups and their geometrical order produce the higher stability in the interaction between the collagen model to the (001) phosphate-rich < (001) and calcium-rich models (Figure 4).
4. DISCUSSION
From the FTIR spectra it can be noticed that only the bands due to apatite and collagen type I are seen, no other major solid phases can be identified in bone tissue.
From thermal analysis, it is possible to conclude that the human bone is thermally the less stable structure studied here (Figure 3). Pure Sigma collagen (from Achilles tendon) is more stable than the collagen extracted from bone. In the case of Sigma collagen, its high stability compared to the one of collagen extracted from bone might be explained by its interaction with bone apatite remnants (as Ca2+ ions) because our extraction method is not the most suitable to obtain pure collagen [18,22]. On the contrary, in bone biomineral these cations interact with the amide groups, resulting in a partial loss of the structure of the collagen. A possible mechanism of the collagen-apatite interaction, is a transfer of the resonant electron density from N to C=O group in the resonant peptide bond [36]. This assumption is supported by changes in the infrared bands amide I (at about 1650 cm−1) and amide II (at about 1550 cm−1) (Figure 2), since these characteristic bands are sensitive to the chemical state of the N-C groups [36]. Furthermore, the electrostatic attraction between the Ca2+ cations and the carbonyl groups, might distort partially the collagen backbone resulting in a decrease in the thermal stability of the molecule. It manifests itself in the change of Tmax (the three thermograms in Figure 3) from 550˚C (Sigma collagen) to two shoulders (in collagen from bone) and finally to 365˚C (bone) and in the distortions of the molecule in the simulation (Figure 5). In other experiments performed with bones demineralized with EDTA [20], the organic phase recovered has its Tmax at 550˚C, as for type I collagen.
The most stable interactions in the simulation among different crystal faces and collagen-like molecules, correspond to the apatite (001)  and Ca2+-rich lattice planes. In these planes, the order of the
and Ca2+-rich lattice planes. In these planes, the order of the  and Ca2+ groups are remarkably in contact with the organic molecule. Indeed in our models (Figure 5), these two (001) planes are the nearest to the molecule’s covalent backbone. This closest interaction might have an effect
and Ca2+ groups are remarkably in contact with the organic molecule. Indeed in our models (Figure 5), these two (001) planes are the nearest to the molecule’s covalent backbone. This closest interaction might have an effect
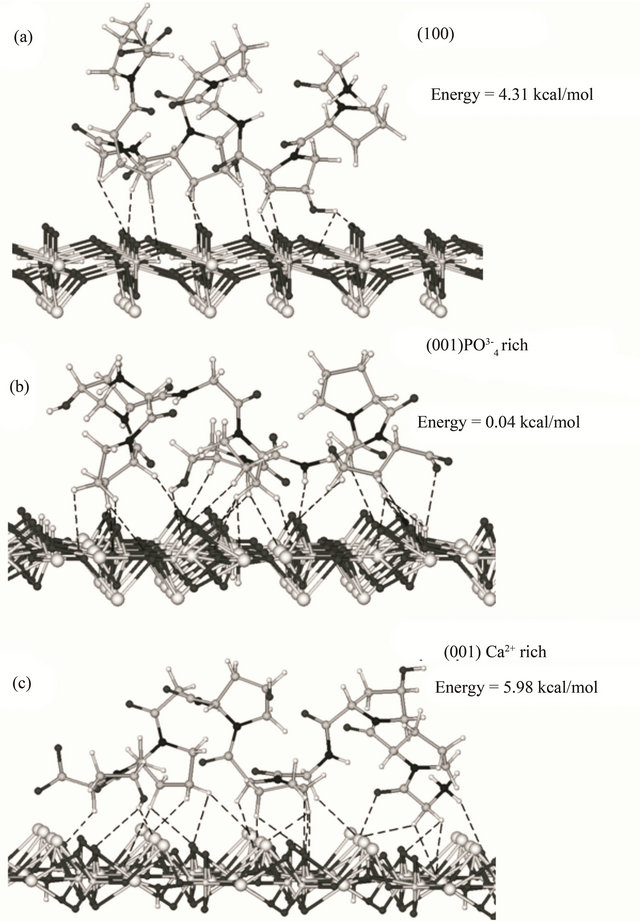
Figure 5. Lowest energy conformations for the model peptide Gly-L-Pro-L-HypGly-L-Pro-L-Hyp-Gly-L-Pro-L-Hyp on hydroxyapatite surfaces, according to MM+ molecular mechanics modelling: (a) (100), (b) phosphate-rich (001), and (c) calcium-rich (001) surface. Dashed lines show contacts closer than 3 Å (10, 24 and 22 contacts, respectively).
on the structure of the peptide and the corresponding infrared spectra in the development and peptide synthesis. For this, time-dependent FTIR studies of bone tissue showed that the amide bands from bone are sensitive to changes in mineralization in function of time [35] corresponding to our assumption. From the above observations we suggest that the collagen molecule changes its physicochemical properties by loosing the thermal stability when it interacts with apatite crystals in the bone tissue. These assumptions derived from the experimental data correlate well with the results of molecular modeling and from the fact that in other sessile organisms the interaction between the biomineral crystallites are mineral bridges conferring structural rigidity as a whole structure [41]. In contrast, the possible dynamic ultrastructure similar to a spring in bone [42] might need less rigidity.
The energy of interaction between the crystal planes and collagen models was plane-dependent, favouring the (001) calcium-rich models, what coincides with our assumption on the role of Ca2+ cations in the hybrid (organic-inorganic) interaction. Another situation the dependency to Ca2+ ion in some proteins of bone, as the osteopontin, seems to be important in the control of the mechanical properties of bone at the molecular scale [43]. This might happen in other collagen-related tissues, as tendon, at different hierarchies studied already by force spectroscopy [44]. It might be possible that the molecular interactions of the type one collagen to the apatite control the order of the collagen I dipole moments in the volume, possibly modifying the piezoelectric behaviour of bone at different structural levels [45].
As a further prospect, in the future it could be important and helpful the use of computational models combined with DSC and FTIR experiments to elucidate the nature of hybrid interactions in biominerals. Additional methods as Atomic Force Microscopy (AFM), used to figure out the different ordering of the structure at the nanoscale, might be useful [46] along with new methods, as Piezoresponse Force Microscopy (PFM) [47]) to bring new information about the organic molecules and their interactions with ions or biominerals.
5. CONCLUSIONS
The mineral phase reduces the thermal stability of collagen in bone, as demonstrated by DSC curves. We attribute this phenomenon to the change of the structure of the covalent backbone in the collagen type I as a result of the interaction with the apatite, potentially with the (001) crystal face.
In our molecular models, the most stable assembly is the  rich surface (0.04 kcal/mol), showing that this arrangement is important for the interaction with bone collagen.
rich surface (0.04 kcal/mol), showing that this arrangement is important for the interaction with bone collagen.
More detailed studies on the interactions of the apatite or related ions with collagen type I and progressive mineralization experiments might help to understand the collagen type I thermal properties at different structural hierarchies giving answers to properties of the biomineral such as piezoelectricity and apatite crystal growth and assembly. These interactions are of crucial importance for explaining and predicting the properties of biominerals. It is relevant the use of AFM and other bionanotechnological methods to identify the differences in adhesion in the main biomineral crystalline planes. It is necessary the use of new nanotechnological methods to elucidate how the highly complex biological nature of peptide exerts controls on the crystal morphology by preferring some crystalline planes to change its properties at different scales. The use of FTIR, DSC, piezoresponse force microscopy and molecular modeling is useful to determine the changes in structure and thermal properties of polymers associated to ions or crystals and can be considered a helpful tool to study biominerals as a whole material.
6. ACKNOWLEDGEMENTS
We thank the National Autonomous University of Mexico for financial support (grant DGAPA-IN100303). A. H. thanks the National Council of Science and Technology of Mexico (CONACyT) and DAAD for scholarships. We are grateful to Margarita Reyes and Sonia Angeles for their technical assistance in SEM studies at Instituto de Geología, UNAM.
NOTES