De Sitter Space as a Computational Tool for Surfaces and Foliations ()
1. Introduction
One of the topics in the theory of foliations is studying geometric properties of leaves e.g. being totally geodesic, totally umbilical, constant mean curvature etc. Two surveys [1,2] by the first author together with Paweł Walczak and Badura descibe progress of this research in the last years.
Conformal geometry using the Sitter space was studied by Langevin and many of his collaborators. Up to now the most extensive explanation is given in [3].
The idea of representing oriented spheres in the de Sitter space is widely presented in [4] by Langevin and Paweł Walczak. They succesfully applied this method to the theory of foliations. Together with Bartoszek they studied properties of so called canal surfaces i.e. envelopes of one parameter families of spheres (cf. [5,6]).
In the paper below we recall some notions of conformal geometry and extend them to study intersections of spheres. The main application is some partial characterizations of totally umbilical foliations on the hyperbolic space 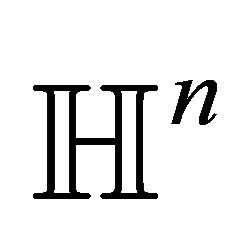 in its conformal ball model.
in its conformal ball model.
2. Space of Spheres
Every 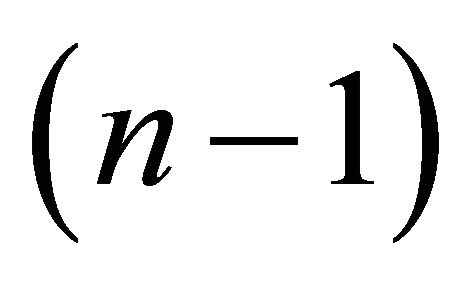 -dimensional round sphere in the Euclidean space
-dimensional round sphere in the Euclidean space 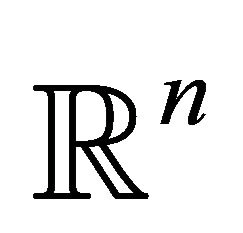 is determined by
is determined by  coordinates of its center and one positive parameter (radius). A hyperplane is the limit of spheres internally tangent to each other when radius tends to infinity. Anyway, in that case there are many different families of spheres having the same limit hyperplane.
coordinates of its center and one positive parameter (radius). A hyperplane is the limit of spheres internally tangent to each other when radius tends to infinity. Anyway, in that case there are many different families of spheres having the same limit hyperplane.
More natural is to consider hyperplanes and spheres on the unit sphere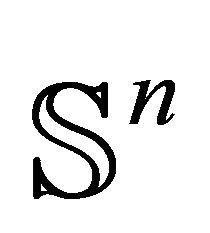 . Here all the hyperplanes and spheres are simply round
. Here all the hyperplanes and spheres are simply round 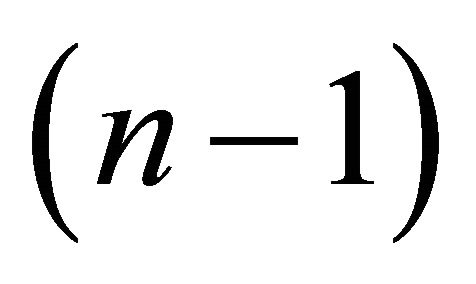 -spheres. Thus the set of
-spheres. Thus the set of  -spheres and hyperplanes in
-spheres and hyperplanes in  is endowed with a differential structure of
is endowed with a differential structure of  -dimensional manifold.
-dimensional manifold.
It is well known that conformal diffeomorphisms of 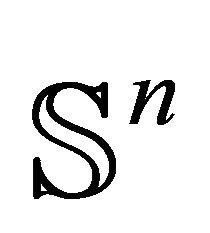 form the Möbius group Möb
form the Möbius group Möb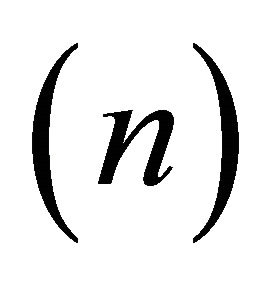 isomorphic to the group
isomorphic to the group 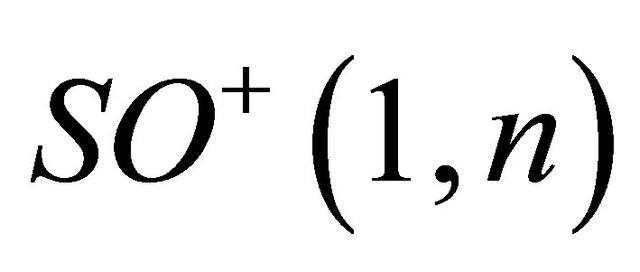 consisting of linear transformations with determinant equal to 1 preserving the Lorentz form and orientation. Thus the Lorentz product preserves all the conformal properties.
consisting of linear transformations with determinant equal to 1 preserving the Lorentz form and orientation. Thus the Lorentz product preserves all the conformal properties.
We shall describe this idea more explicitely.
Consider 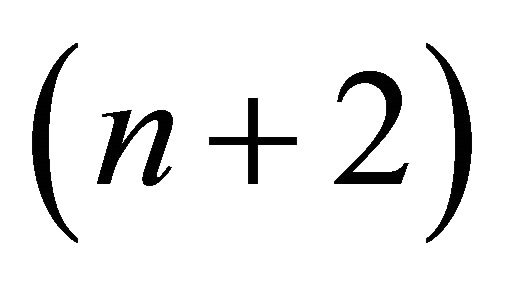 -dimensional Lorentz space
-dimensional Lorentz space , i.e. the space
, i.e. the space 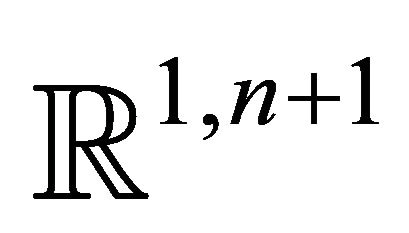 with the Lorentz form
with the Lorentz form 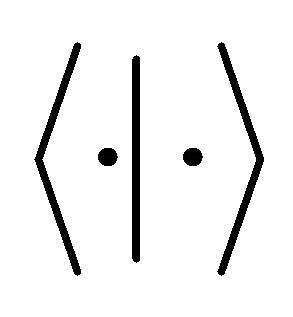 given by
given by
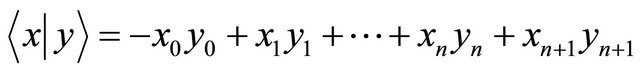
In 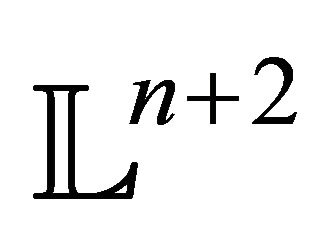 the canonical basis
the canonical basis 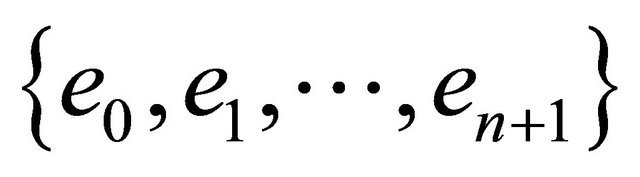 is considered.
is considered.
For  we use the notation
we use the notation
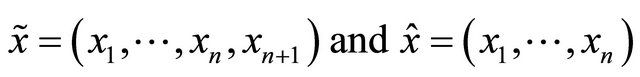
The terminology comes from the special relativity, so we traditionally say that vectors of positive Lorentz norm (i.e.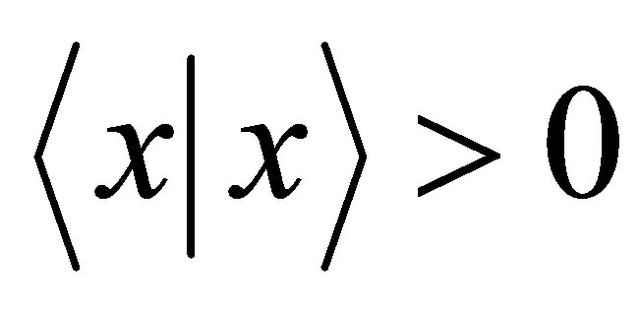 ) are called space-like while those of negative (resp. zero) Lorentz norm are time-like (resp. light-like).
) are called space-like while those of negative (resp. zero) Lorentz norm are time-like (resp. light-like).
On the space-like  -plane
-plane 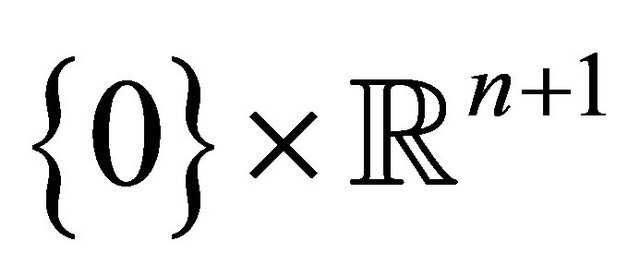 the Lorentz form reduces to the standard scalar product
the Lorentz form reduces to the standard scalar product  and the respective Euclidean norm
and the respective Euclidean norm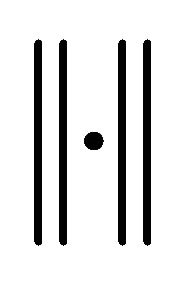 .
.
Definition 1 The sets
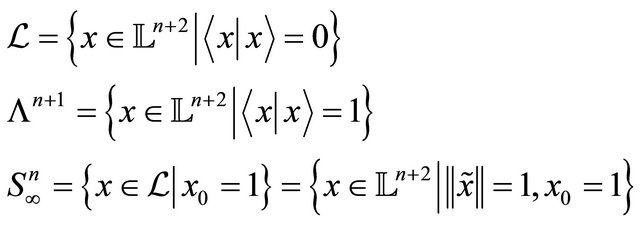
are called respectively: the light cone, the de Sitter 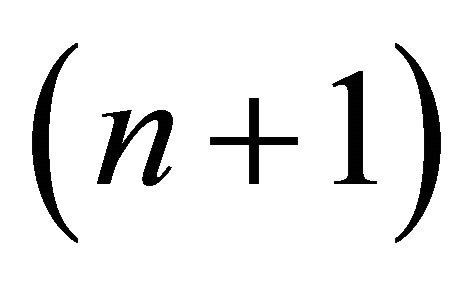 -space, the limit sphere.
-space, the limit sphere.
Furthemore we denote by S the set of oriented (round) 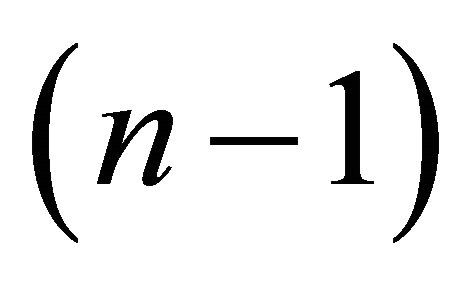 -spheres contained in
-spheres contained in 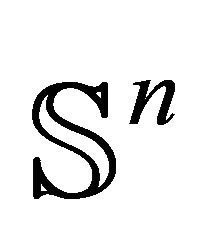 which is in fact
which is in fact .
.
Proposition 2 Assigning to any 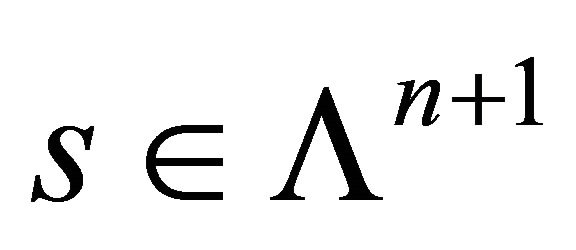 an intersection
an intersection 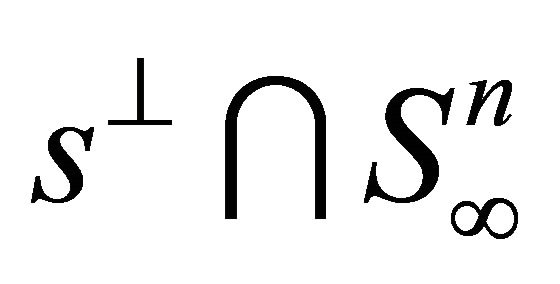 is an one-to-one correspondence between
is an one-to-one correspondence between 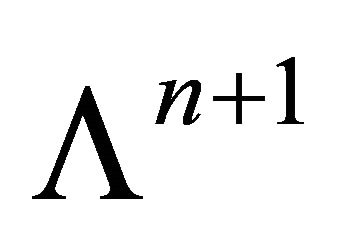 and S.
and S.
Proof: Observe that for  we have
we have
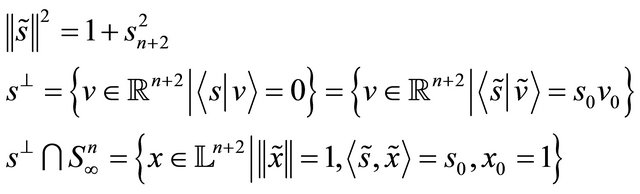
Since in the affine hyperplane 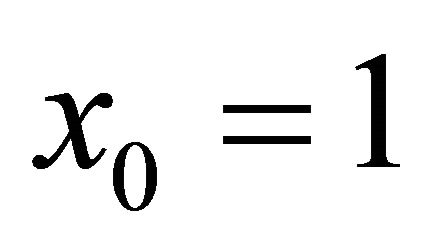 the distance from an
the distance from an 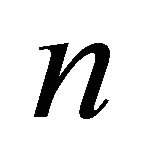 -plane
-plane 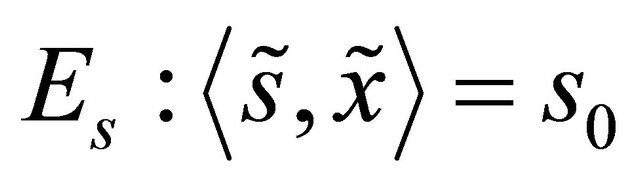 to the origin
to the origin 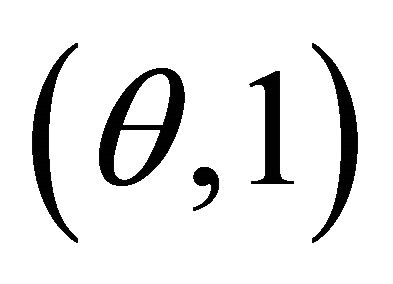 equals
equals
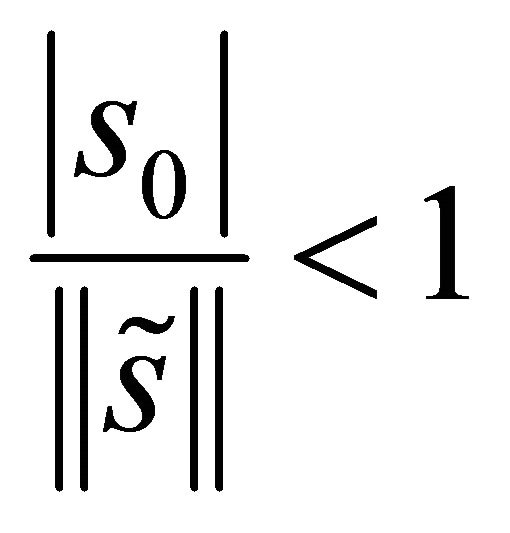
hence  intersects the sphere
intersects the sphere  along
along  - sphere what is clearly visible in Figure 1.
- sphere what is clearly visible in Figure 1.
The 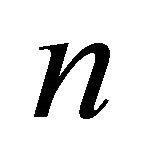 -planes
-planes 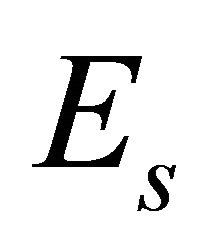 and
and  (and therefore respective
(and therefore respective 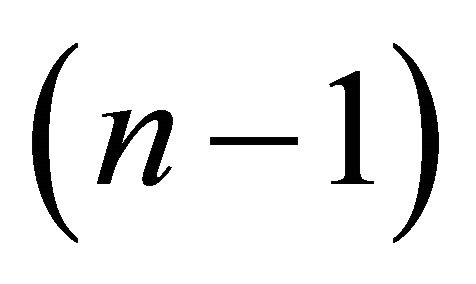 -spheres) are equal if
-spheres) are equal if 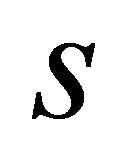 and
and 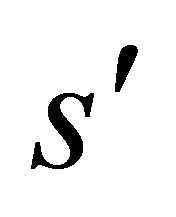 are linearly dependent. But
are linearly dependent. But  intersects every 1-dimensional vector space
intersects every 1-dimensional vector space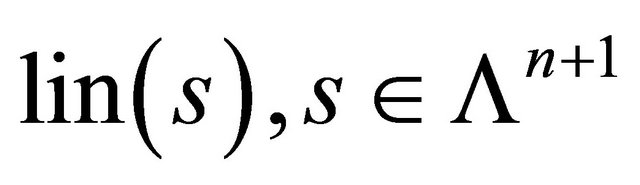 , in exactly two points, so we can think of them as of distinct orientations of the sphere
, in exactly two points, so we can think of them as of distinct orientations of the sphere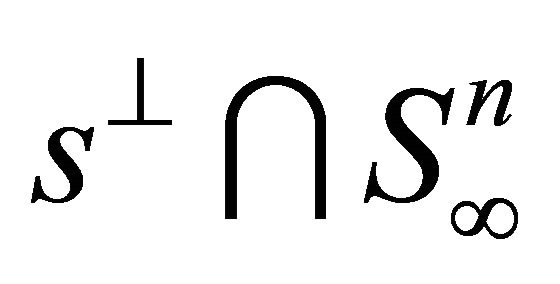 .
.
The above proposition motivates.
Definition 3 Given  we say that
we say that 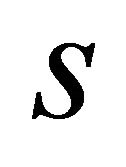 is the representation of sphere
is the representation of sphere  in the de Sitter
in the de Sitter 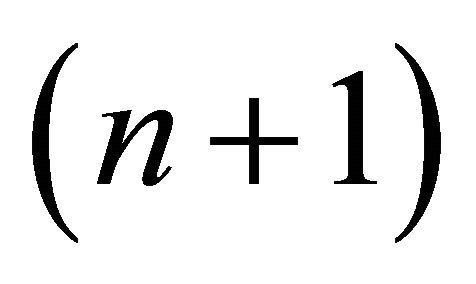 -space.
-space.
Since we are interested only in conformal properties of spheres (mainly angle of intersection), we shall proceed with stereographic projection which transforms them conformally onto codimension 1 spheres or affine subspaces.
Proposition 4 Assume that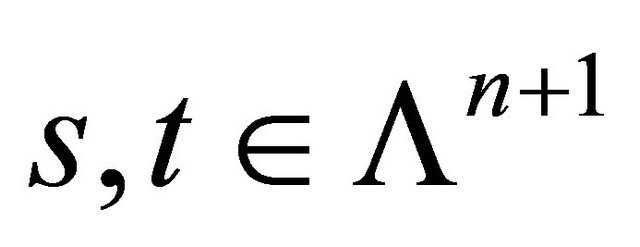 . Then spheres
. Then spheres 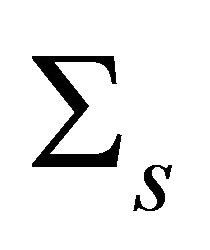 and
and 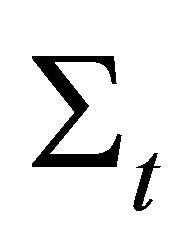 represented by them:
represented by them:
1) are disjoint if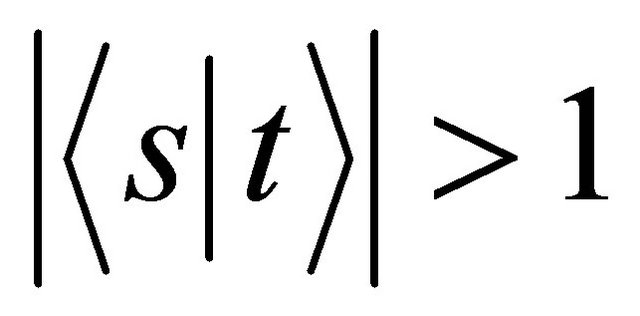 2) meet at angle
2) meet at angle  if
if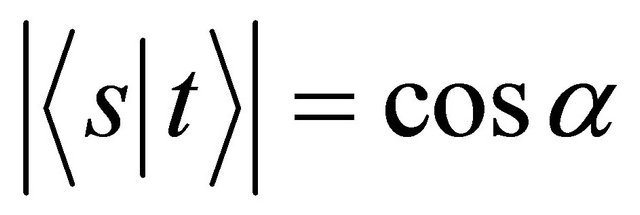 .
.
Proof: The Lorentz form is invariant under Möbius transformations so it is enough to check the statement for spheres (not) meeting a fixed sphere.
Fix the sphere represented by 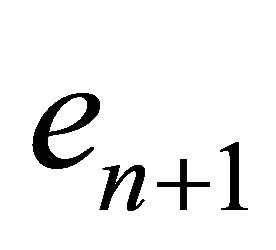 and observe that
and observe that
 for any
for any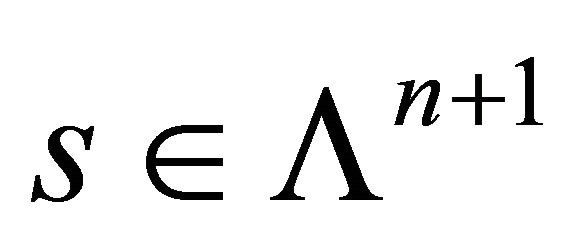 . Let
. Let  denote the stereographic projection of
denote the stereographic projection of 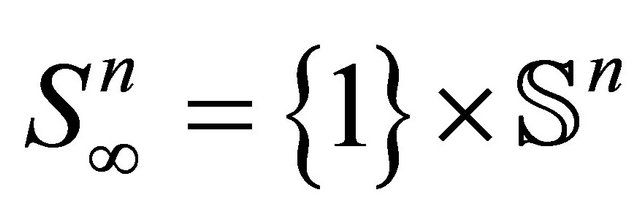 onto
onto 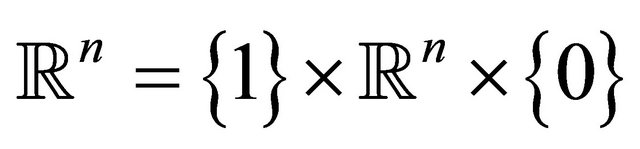 from the point
from the point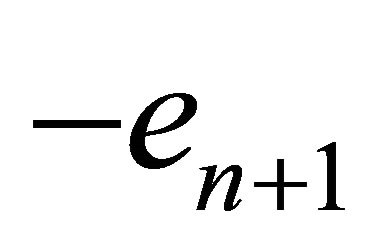 .
.
Thus the projection  is given by the formula
is given by the formula
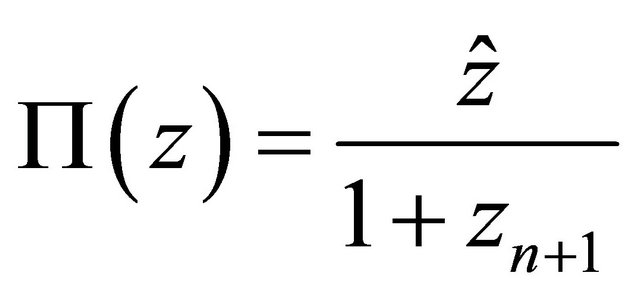
and its inverse by

It is obvious that 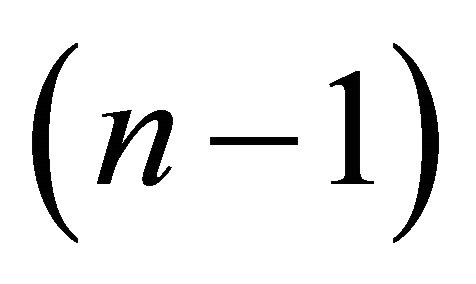 -sphere
-sphere 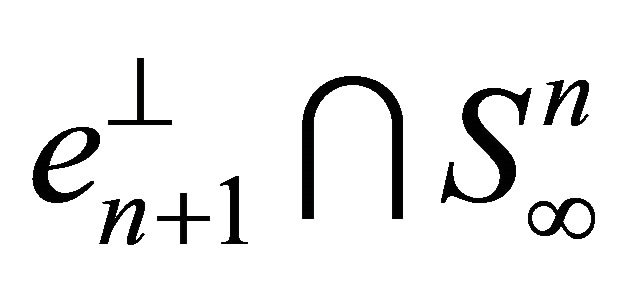 is invariant under
is invariant under .
.
For  we have an equation of
we have an equation of 

or equivalently

Hence two cases occur:
1) If  then
then  is a hyperplane
is a hyperplane
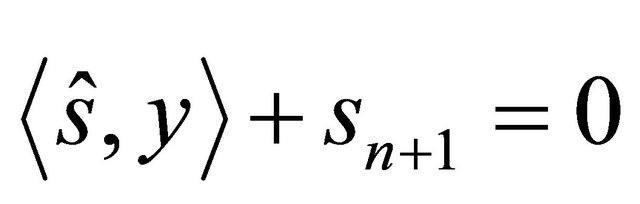 2) If
2) If 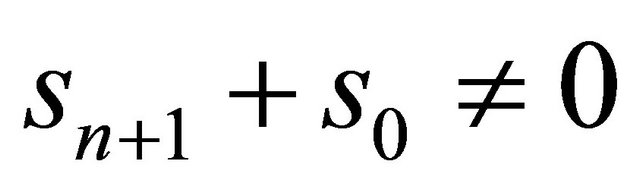 then
then  is the sphere
is the sphere
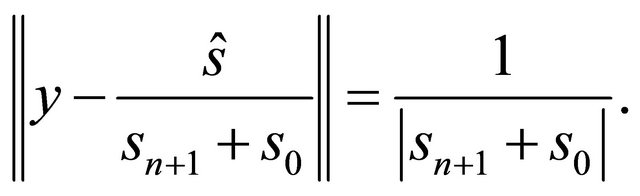
For the angle of intersection we obtain:
1) In case of a hyperplane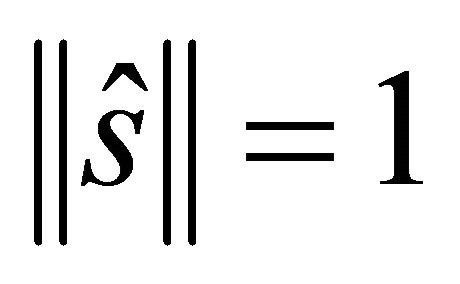 ) so
) so 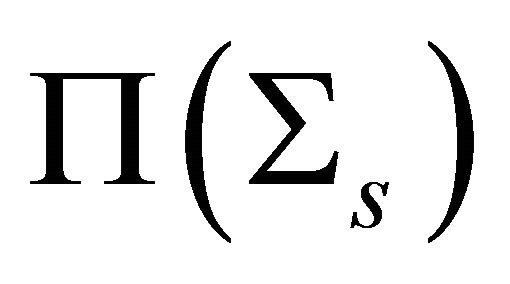 meets the unit sphere at angle
meets the unit sphere at angle  if the Euclidean distance of the center from
if the Euclidean distance of the center from 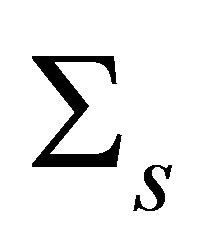 equals
equals . Thus we have
. Thus we have
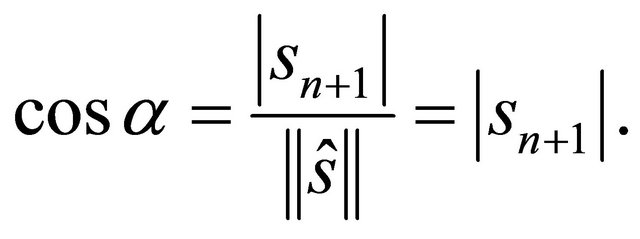
2) If  is a sphere then it meets the unit sphere at angle
is a sphere then it meets the unit sphere at angle 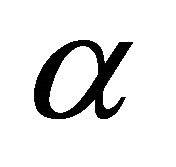 if at any point of intersection the angle at this point in the triangle formed by centers is exactly
if at any point of intersection the angle at this point in the triangle formed by centers is exactly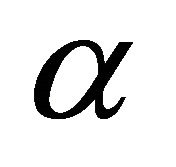 . Equivalently, by law of cosines
. Equivalently, by law of cosines
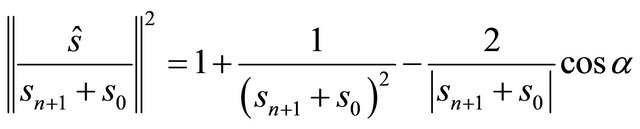
which could be simplified to
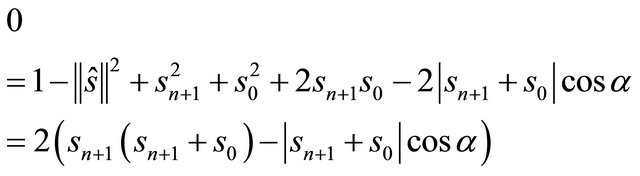
or directly 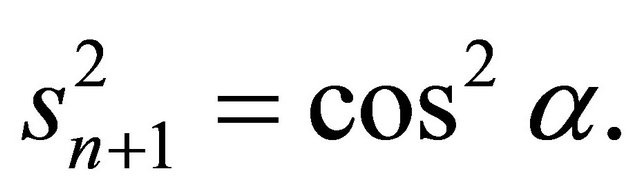
Example 5
1) 2-dimensional de Sitter space  is one-sheeted hyperboloid in 3-dimensional space. Points of
is one-sheeted hyperboloid in 3-dimensional space. Points of 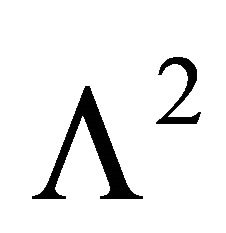 represent 0-dimensional oriented spheres on the unit circle. Thus they are arcs of this circle. According to Prop. 4 a) these arcs are disjoint if the Lorentz product of their representations is
represent 0-dimensional oriented spheres on the unit circle. Thus they are arcs of this circle. According to Prop. 4 a) these arcs are disjoint if the Lorentz product of their representations is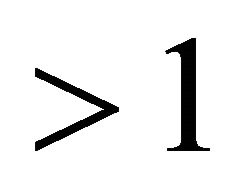 b) they are nested if the product is
b) they are nested if the product is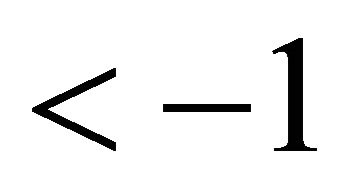 c) they are knotted if the product is between −1 and 1.
c) they are knotted if the product is between −1 and 1.
Excluding the case of representing the same unoriented sphere the product equal −1 means that one arc is include-ed in another, while 1 is the condition for having exactly one point in common.
2) Oriented circles (i.e. discs) on 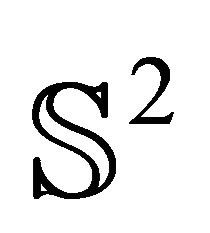 are represented in
are represented in . The circles have 2 (resp. 1, 0) common points provided that the absolute value of their Lorentz product is in
. The circles have 2 (resp. 1, 0) common points provided that the absolute value of their Lorentz product is in  (resp. 1,
(resp. 1,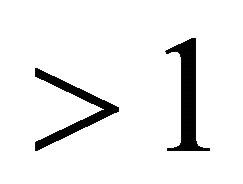 ).
).
3) 2-dimensional spheres on 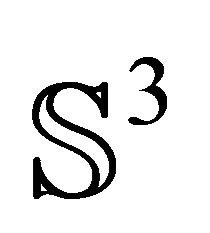 are tangent if their representations on
are tangent if their representations on  have the Lorentz product equal
have the Lorentz product equal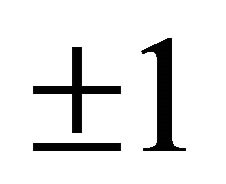 . They intesect along a circle if the product is between −1 and 1. Otherwise they are nested.
. They intesect along a circle if the product is between −1 and 1. Otherwise they are nested.
3. Application to Foliations
3.1. Umbilical Foliations of 
Hyperbolic 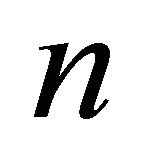 -space
-space 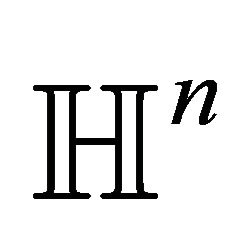 has the Poicaré ball model which is the unit
has the Poicaré ball model which is the unit 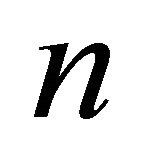 -ball with conformally changed Euclidean metric. At every point
-ball with conformally changed Euclidean metric. At every point  the Euclidean Riemannian metric is multiplied by
the Euclidean Riemannian metric is multiplied by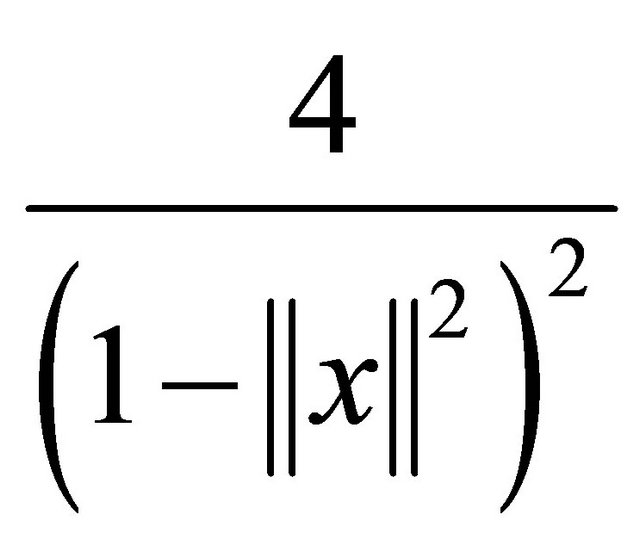 . The ball model is conformal so angles at
. The ball model is conformal so angles at 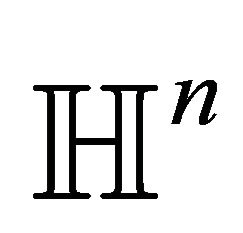 are preserved.
are preserved.
Complete totally umbilical hypersurfaces in the Euclidean space are spheres and hyperplanes. Conformality of the ball model implies the same is true for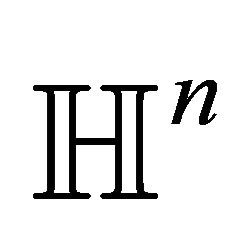 . Thus every totally umbilical hypersurface in the ball model is intersection of
. Thus every totally umbilical hypersurface in the ball model is intersection of 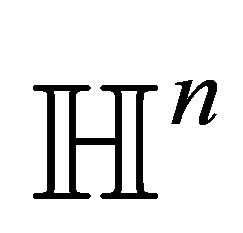 with a (Euclidean) sphere or a (Euclidean) hyperplane.
with a (Euclidean) sphere or a (Euclidean) hyperplane.
If we denote by 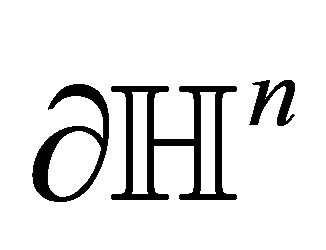 the ideal boundary of
the ideal boundary of 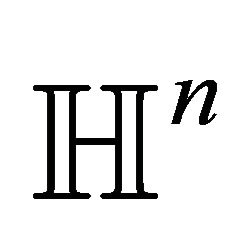 which is in fact
which is in fact 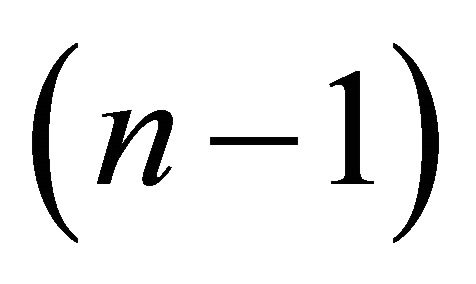 -sphere then spheres orthogonal to
-sphere then spheres orthogonal to 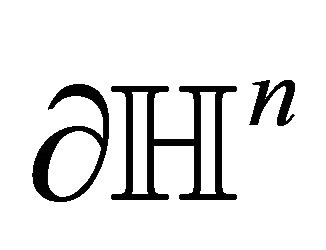 contain totally geodesic hypersurfaces. Moreover, every sphere making angle
contain totally geodesic hypersurfaces. Moreover, every sphere making angle 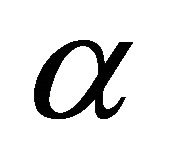 with
with 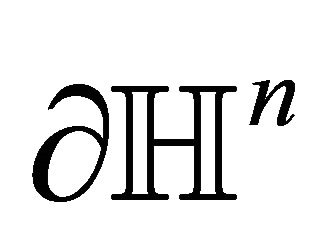 contains a hypersurfaces with all principal curvatures equal to
contains a hypersurfaces with all principal curvatures equal to 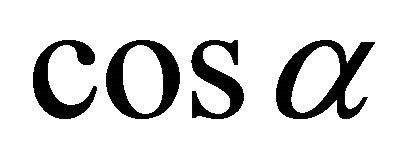 sharing ideal boundary with a totally geodesic hypersurface from which a given part of the sphere is equidistant.
sharing ideal boundary with a totally geodesic hypersurface from which a given part of the sphere is equidistant.
Geodesic spheres in 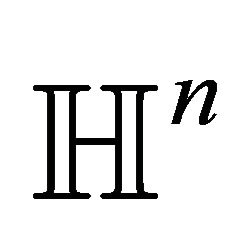 do not touch the ideal boundary. They bound balls which cannot be foliated by spheres in codimension 1 which allows us to exclude them from the further analysis. From now on we shall study only unbounded totally umibilical hypersurfaces.
do not touch the ideal boundary. They bound balls which cannot be foliated by spheres in codimension 1 which allows us to exclude them from the further analysis. From now on we shall study only unbounded totally umibilical hypersurfaces.
This makes sense to analyse totally umbilical hypersurfaces of 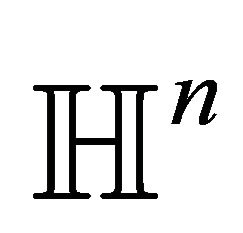 as well as codimension
as well as codimension  totally umbilical foliations using only notions for spheres coming from
totally umbilical foliations using only notions for spheres coming from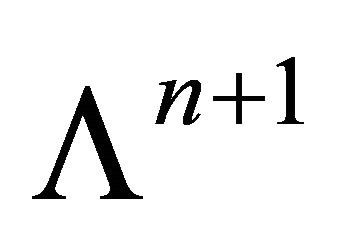 .
.
Choose a model for  as
as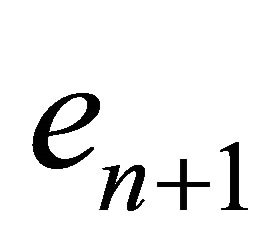 . This oriented
. This oriented 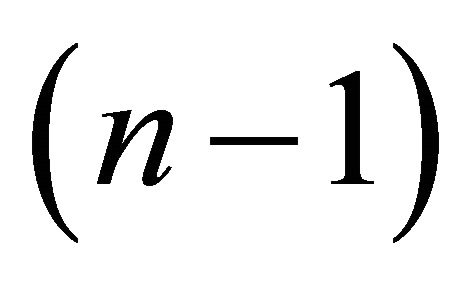 -sphere could be treated as a unit ball. From Prop. 4 and its proof we obtain directly.
-sphere could be treated as a unit ball. From Prop. 4 and its proof we obtain directly.
Corollary 6 Assume that 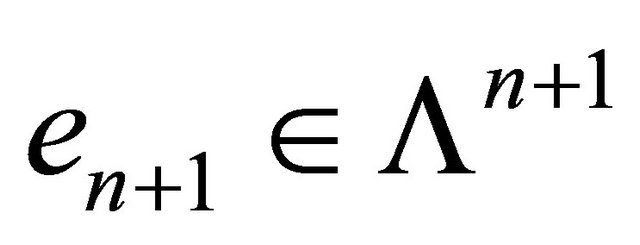 is a ball model of
is a ball model of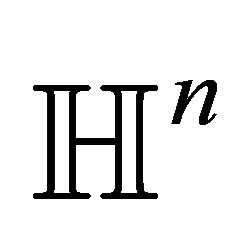 . An element
. An element 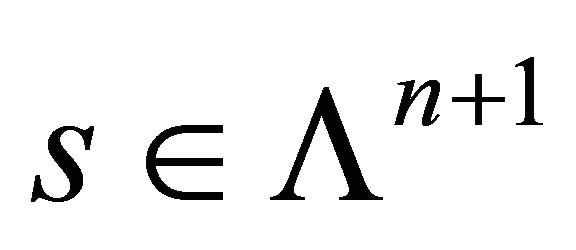 represents an unbounded totally umbilical hypersurface of
represents an unbounded totally umbilical hypersurface of 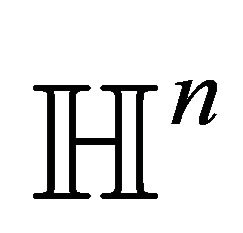 if
if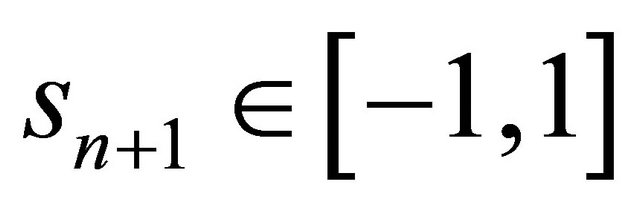 . Moreover, the element
. Moreover, the element  represents:
represents:
1) a totally geodesic hypersurface if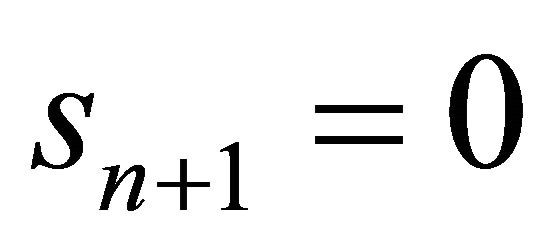 2) a hypersphere meeting ideal boundary at angle
2) a hypersphere meeting ideal boundary at angle  if
if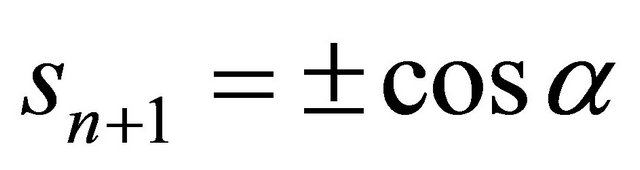 3) a horosphere which is internally tangent to the ideal boundary if
3) a horosphere which is internally tangent to the ideal boundary if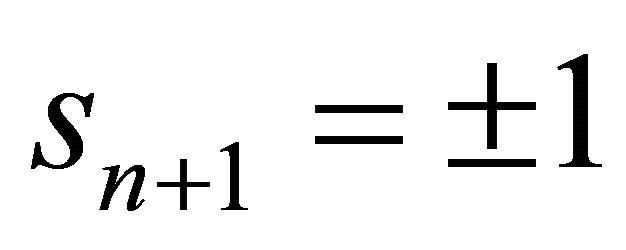 .
.
Every unbounded totally umbilical hypersurface of  divides the hyperbolic space into two domains with nonempty ideal boundary. From this we conclude that every totally umbilical codimension 1 foliation of
divides the hyperbolic space into two domains with nonempty ideal boundary. From this we conclude that every totally umbilical codimension 1 foliation of 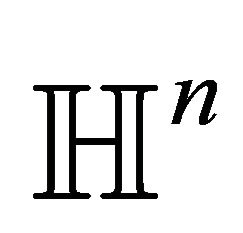 has leaves entirely contained in spheres which form oneparameter family.
has leaves entirely contained in spheres which form oneparameter family.
Corollary 7 Every totally umbilical codimension 1 foliation of  is represented by a curve
is represented by a curve 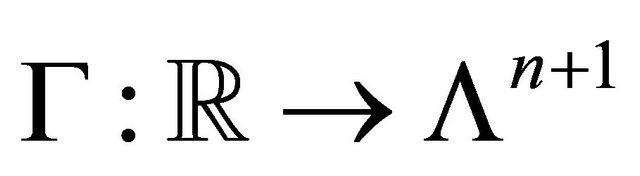 which lies in the region bounded by hyperplanes
which lies in the region bounded by hyperplanes .
.
Denote by 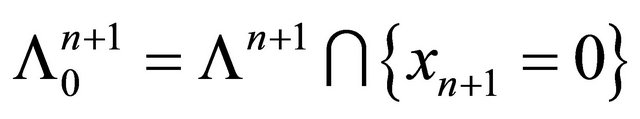 the set of totally geodesic hypersurfaces and by
the set of totally geodesic hypersurfaces and by 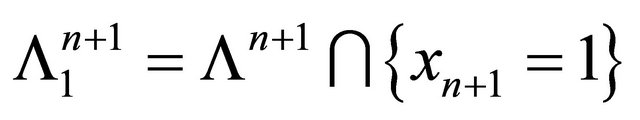
—the set of horospheres. It is easy to see that 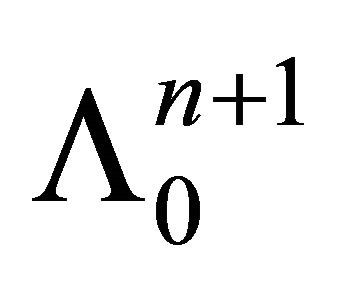 is simply
is simply  -dimensional de Sitter space
-dimensional de Sitter space 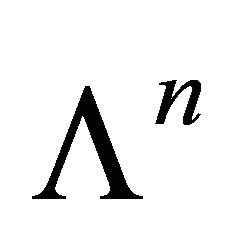 while
while 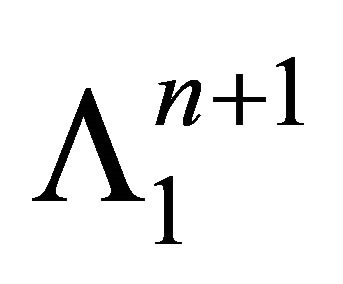 is the light cone corresponding to
is the light cone corresponding to 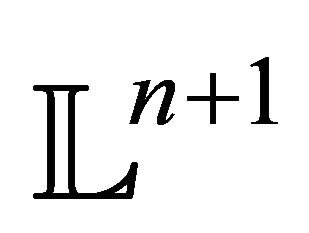 with the vertex
with the vertex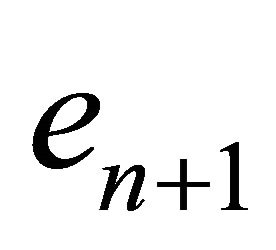 . Similarly, the set of totally umbilical hypersurfaces with the mean curvature equal to
. Similarly, the set of totally umbilical hypersurfaces with the mean curvature equal to  is rescaled
is rescaled  - dimensional de Sitter space given by
- dimensional de Sitter space given by 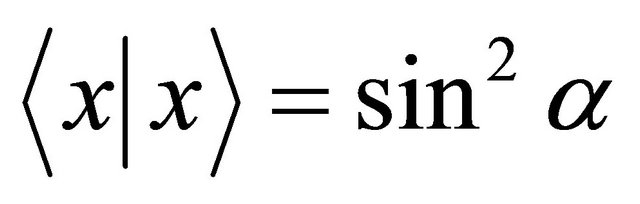 for the first
for the first 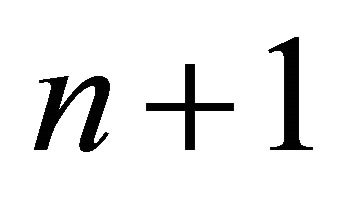 coordinates.
coordinates.
The converse to Cor. 7 is obviously not true. Some local conditions are studied by Langevin and the first author in [7]. More global conditions were found for totally geodesic foliations (see e.g. Figure 2).
Theorem 8 (Cz, Langevin [7]) Any unbounded curve 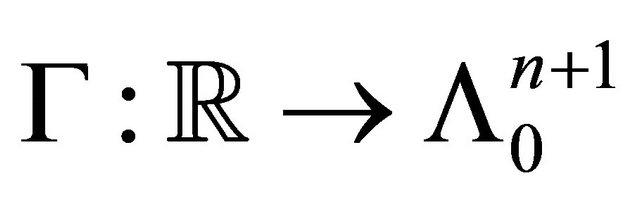 such that
such that
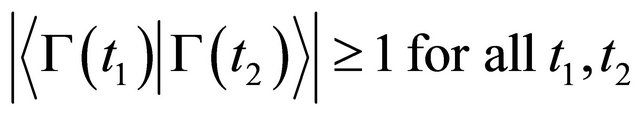
represents a totally geodesic codimension 1 foliation of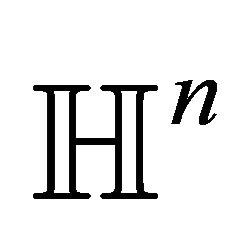 . Moreover, any such foliation is transversely oriented and is represented by a curve
. Moreover, any such foliation is transversely oriented and is represented by a curve  as above.
as above.
The proof uses mainly the fact that spheres orthogonal to a given sphere are disjoint inside this sphere if they are at most tangent on the given sphere.
The above works even for 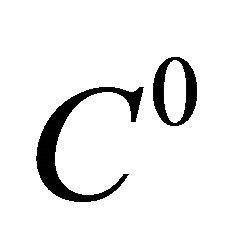 foliations. For differentiable case we have the following Corollary 9 An unbounded
foliations. For differentiable case we have the following Corollary 9 An unbounded 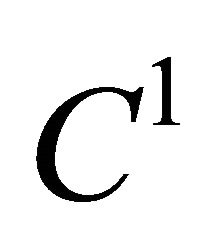 curve
curve  represents a totally geodesic codimension 1 foliations of
represents a totally geodesic codimension 1 foliations of 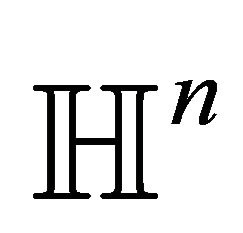 if
if  is time-or-light-like i.e.
is time-or-light-like i.e. 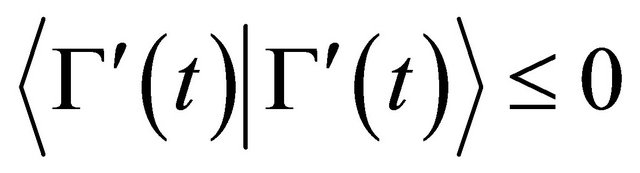 for any
for any .
.
Strictly metrical characterization of totally umbilical foliations of  were described by Lużyńczyk and the first author in [8] under assumption that an orthogonal transversal is a geodesic.
were described by Lużyńczyk and the first author in [8] under assumption that an orthogonal transversal is a geodesic.
Example 10 Well known examples of totally umbilical foliations of 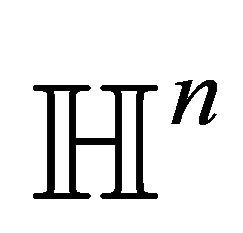 are those by horospheres of the same end, totally geodesic orthogonal to a given geodesic or to a horocycle.
are those by horospheres of the same end, totally geodesic orthogonal to a given geodesic or to a horocycle.
1) A light ray of the shifted light cone 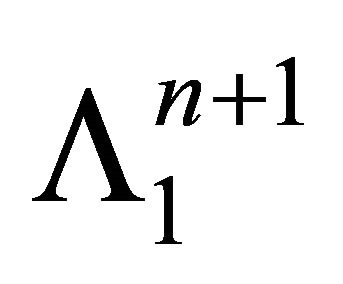 repre-
repre-
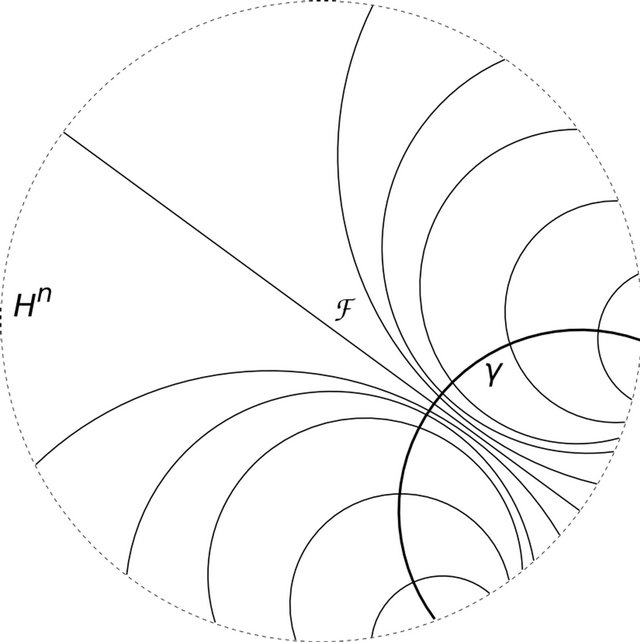
Figure 2. Totally geodesic foliation  orthogonal to a geodesic
orthogonal to a geodesic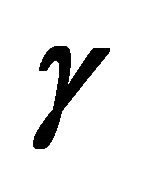 .
.
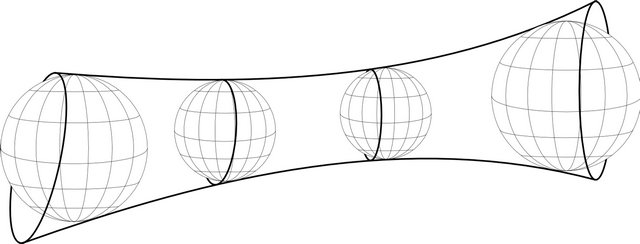
Figure 3. A canal surface with its spheres.
sents a foliation by horospheres with the same endpoint on the ideal boundary.
2) The intersection of de Sitter 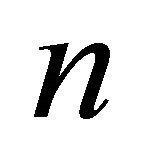 -space
-space 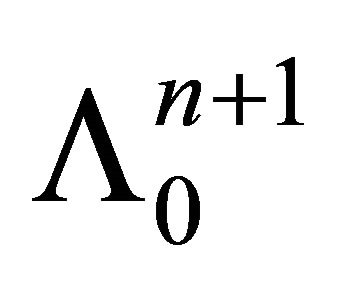 with the time-like plane
with the time-like plane 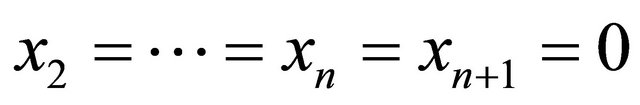 represents a totally geodesic foliation orthogonal to a geodesic.
represents a totally geodesic foliation orthogonal to a geodesic.
3) The intersection of de Sitter 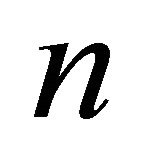 --space
--space  with the space-like plane
with the space-like plane 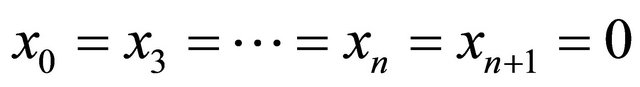 represents a totally geodesic foliation orthogonal to a horocycle.
represents a totally geodesic foliation orthogonal to a horocycle.
3.2. Foliatons by Surfaces
Some of hypersurfaces are envelopes of families of spheres. In particular, envelopes of one-parameter families of 2-spheres are objects which are well understable. They are easily represented as curves in de Sitter space .
.
Definition 11 An envelope of an one-parameter family of 2-spheres is called a canal surface.
If a canal surface is a common envelope of two distinct one-parameter families of spheres we say that this surface is a Dupin cyclide.
Typical examples of a canal surface are a torus, a round cylinder, a cone of revolution or more generally a regular surface of revolution. A conformal image of a cylinder with a family of generating spheres is shown on Figure 3.
Dupin cyclides could characterized in another way as conformal images of tori, cylinders and cones.
In [5,6] the authors characterized foliations of  with canal leaves proving that such foliation comes only from the Reeb foliation by inserting a torical region filled out by tori and cylinders.
with canal leaves proving that such foliation comes only from the Reeb foliation by inserting a torical region filled out by tori and cylinders.
Some sophisticated methods led Langevin and Paweł Walczak to the fact that foliating compact hyperbolic 3-manifold is impossible neither by umbilical nor Dupin leaves.
NOTES
2010 Mathematics Subject Classification: 53C12, 53A05, 53A35, 53A30, 53C50.