1. Introduction
The calculations on the virial theorem are done to obtain an equation explaining the relations between the kinetic energy and potential energy of a particle and an equation describing the maximum distance travelled by this particle in a stable system. In Section 2, these equations are obtained due to the calculations. The previous works are searched. It was realized that the Equations (13) and (16) are first presented in this study. The calculations done in this study will be useful in astronomy. In Section 3, the results of this study are discussed.
2. Calculations
The virial theorem gives the general equation between kinetic energy and potential energy of a stable system of n particles bound by potential forces. R. J. E. Claussius formulated the virial theorem in 1870 after twenty years long study [1]. The word “virial” comes from the Latin word vis which means “force” or “energy”. The reader who likes to learn more about the virial theorem is recommended to see the book [2]. The article [3] includes an extensive research on the virial theorem. The article [4] includes a search about finite deformations in the boundary conditions.
For system of masses at points 
the equations of motion are;
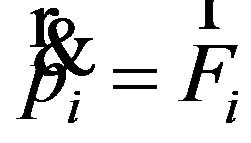(1)
A quantity G is defined in [5] as:
(2)
The time derivative of this quantity is
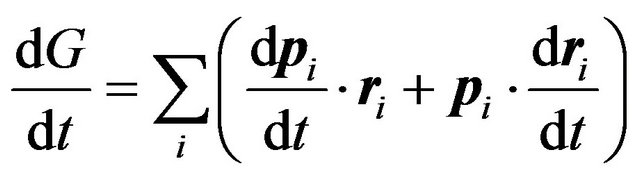(3)
where
(4)
In Equations (3) and (4) T is the kinetic energy, m is the mass of the particle, p is the momentum related to the particle, F is the force acting on the particle, and r is the distance vector of the particle. We are going to obtain the virial theorem from the Equations (3) and (4) as below.
For a bounded quantity G, in a time interval of
, one can write:
(5)
and
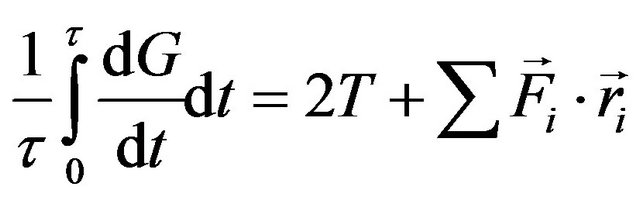(6)
if the momentum is periodic. Then we get the virial theorem as
(7)
Writing T as
(8)
and dropping the summation sign, the Equation (7) is written in the form:
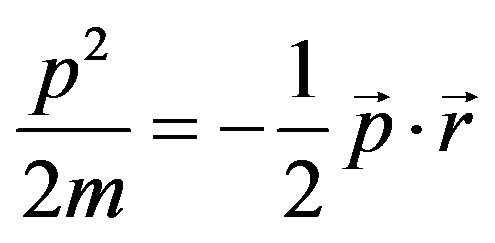(9)
In [6] the force is related to the Hamiltonian by
(10)
The scalar product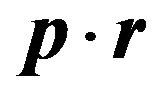 
has to result in a scalar quantity. Therefore, the vector r changes to the distance r in the following equations. By using this, the Equation (9) is written as
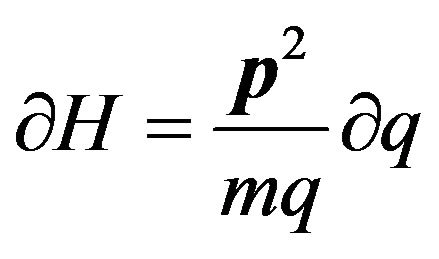(11)
Here, the notation 
is used as the differential d. Integrating this equation we get
(12)
For a particle moving with constant speed and using H = E = T + V and q = r one can integrate from r0 to r to find the relation between kinetic energy T and potential energy V in time averaged values as
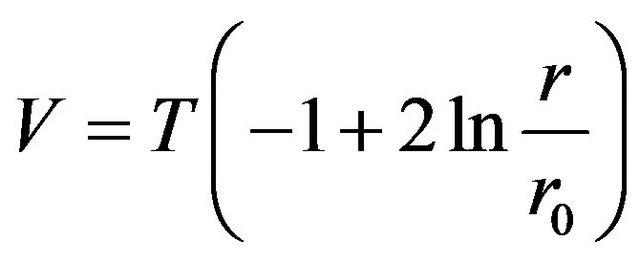(13)
For circular motion the equation is
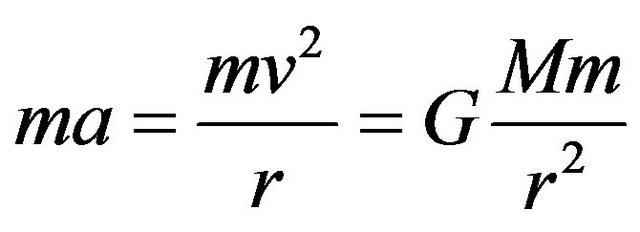(14)
In this case, the Equation (12) gives the correct classical gravitational potential energy if we integrate it from 
;
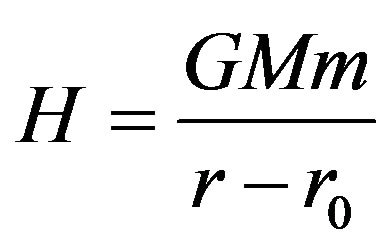(15)
If we relate to this study, M is the mass of the set of particles in the system and m is the mass of the particle under consideration. The Equation (13) can be written as
(16)
This is the equation for the kinetic energy T of a particle in a stable system at distance r from the origin of the system. E is the total energy of the particle, and 
is the initial distance of the particle from the origin of the system.
3. Conclusion
The Equation (16) derived in this study explains that the distance of a moving particle in a stable system has a maximum distance r if it remains in the system. The maximum distance must be the distance from the origin of the system to the outer surface of the system at most. When something moves away from the distance to the outer surface, it is out of the system. In other words, it can be said that; when this is reached, the stability of the system is destroyed or the travelled body is not a member of the system. The Equations (13) and (16) are first derived here comparing to the previous works.
4. Acknowledgements
I would like to thank to Prof. Dr. Amirullah Mamedov for his valuable discussion.