Sufficient Fritz John Type Optimality Criteria and Duality for Control Problems ()
1. Introduction
Optimal control models represent a variety of common situations, notably, advertising investment, production and inventory, epidemic, control of a rocket, etc. The optimal planning of a river system which is an invincible resource of nature, where it is needed to make the best use of the water, can also be modelled as an optimal control problem. Optimal control models are also potentially applicable to economic planning and to the world models of the “Limits to Growth” kind in general.
Optimality criteria for any optimization problem are of great significance and lay the foundation of the concept of duality. Fritz John optimality criteria for a control problem were first derived by Berkovitz [1]. Subsequently Mond and Hanson [2], who first investigated duality in optimal control pointed out that from Fritz John optimal criteria, Karush-Kuhn-Tucker optimality criteria can be deduced if normality of the solution of a control problem which replaces a regularity conditions is assumed. Later, treating a nondifferentiable control problem as a nondifferentiable mathematical programming problem in an infinite-dimensional space, Chandra et al. [3], obtained Fritz John as well as Karush-Kuhn-Tucker optimality criteria.
For a nondifferentiable control problem Using KarushKuhn-Tucker optimality criteria, they formulated Wolfe type dual and derived usual duality results under appropriate convexity assumptions.
In this research exposition, sufficient Fritz John criteria are derived for a differentiable control problem in which objective functional is pseudoconvex and constraint functions are quasiconvex or semi-strictly pseudoconvex. A number of duality results are proved for relating the solution of the control problem with that of its proposed dual under suitable generalized convexity requirements. The relationship of our duality results to those of a nonlinear programming problem is indicated.
2. Control Problem and Related Preliminaries
Let denotes a n-dimensional Euclidean space,
denotes a n-dimensional Euclidean space, 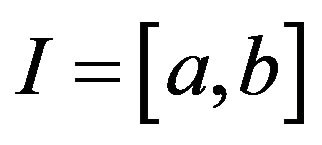 be a real interval and
be a real interval and  be a continuously differentiable with respect to each of its arguments. For the function
be a continuously differentiable with respect to each of its arguments. For the function  where
where  is differentiable with its derivative
is differentiable with its derivative 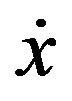 and
and  is the smooth function, denote the partial derivatives of
is the smooth function, denote the partial derivatives of  by
by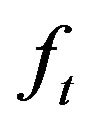 ,
,  and
and , where
, where

For m-dimensional vector function  the gredient with respect to
the gredient with respect to  is
is

a  matrix of first order derivatives.
matrix of first order derivatives.
Here 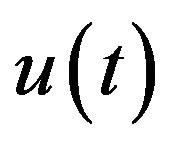 is the control variable and
is the control variable and  is the state variable,
is the state variable,  is related to
is related to  via the state equation
via the state equation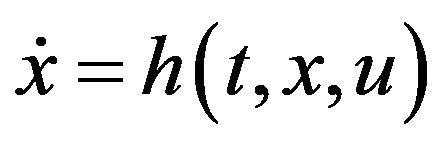 . Gradients with respect to
. Gradients with respect to  are defined analogously.
are defined analogously.
A control problem is to transfer the state vector from an initial state  to a final state
to a final state  so as to minimize a functional, subject to constraints on the control and state variables.
so as to minimize a functional, subject to constraints on the control and state variables.
A control problem can be stated formally as(CP):  subject to
subject to
 (1)
(1)
 (2)
(2)
 (3)
(3)
1) 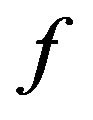 is as before,
is as before,  and
and  are continuously differentiable functions with respect to each of its arguments.
are continuously differentiable functions with respect to each of its arguments.
2) X is the space of continuously differentiable state functions  such that
such that  equipped with the norm
equipped with the norm , and
, and  is the space of piecewise continuous control functions
is the space of piecewise continuous control functions  has the uniform norm
has the uniform norm  and 3) The differential Equation (2) for
and 3) The differential Equation (2) for  with the initial conditions expressed as
with the initial conditions expressed as  may be written as
may be written as 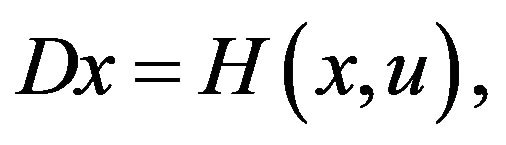 where the map
where the map  being the space of continuous functions from
being the space of continuous functions from , defined by
, defined by 
Following Craven [4], the control problem can be expressed as(ECP):  subject to
subject to


where  is function from
is function from  into
into  given by
given by  from
from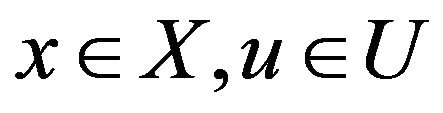 , and
, and ;
;  is the convex cone of functions in
is the convex cone of functions in  whose components are non-negative; thus
whose components are non-negative; thus 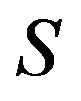 has interior points.
has interior points.
Necessary optimality conditions for existence of extermal solution for a variational problem subject to both equality and inequality constraints were given by valentine [5]. Invoking Valentine’s [5] results, Berkovitz [1] obtained corresponding necessary optimality criteria for the above control problem (CP). Here we state the Fritz John type optimality conditions derived by Chandra et al. [3] in of the following proposition which will be required in the sequel.
Proposition 1
(Necessary Optimality Conditions)
If  an optimal solution of (CP) and the Frechet derivatives
an optimal solution of (CP) and the Frechet derivatives 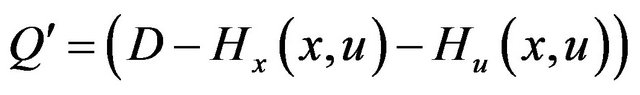 is surjective, then there exist Lagrange multipliers
is surjective, then there exist Lagrange multipliers , and piecewise smooth functions
, and piecewise smooth functions 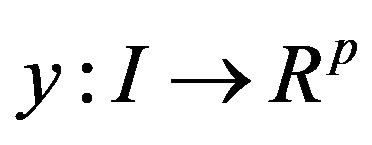 and
and  satisfying, for all
satisfying, for all ,
,
 (4)
(4)
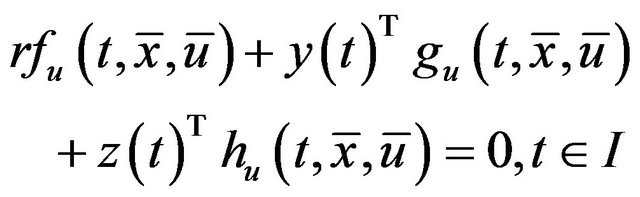 (5)
(5)
 (6)
(6)
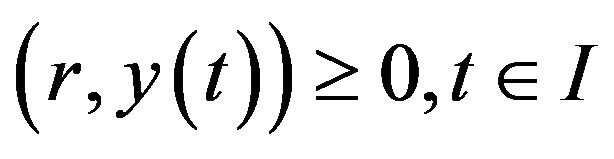 (7)
(7)
 (8)
(8)
The above conditions will become Karush-Kuhn-Tucker conditions if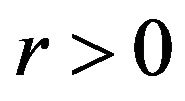 . Therefore, if we assume that the optimal solutions
. Therefore, if we assume that the optimal solutions  is normal, then without any loss of generality, we can set
is normal, then without any loss of generality, we can set . Thus from the above we have the Karush-Kuhn-Tucker type optimality conditions
. Thus from the above we have the Karush-Kuhn-Tucker type optimality conditions

Using these optimality conditions, Mond and Hanson [2] constructed following Wolfe type dual.
(CD):  subject to
subject to

In [6], [CP] and (CD) are shown to from a dual pair if ,
, 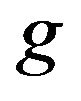 and
and  are all convex in
are all convex in 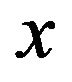 and
and . Subsequently, Mond and Smart [6] extended this duality under generalized invexity.
. Subsequently, Mond and Smart [6] extended this duality under generalized invexity.
As a follows up, Husain et al. [7] formulated the following dual (CD) to the primal problem (CP) in the spirit of Mond and Weir [8].
(CD): Maximize 
subject to

They proved sufficiency of the optimality criteria and duality for the pair of dual problems (CP) and (CD) under pseudoinvexity of  and quasi-invexity of
and quasi-invexity of
 .
.
3. Sufficiency of Fritz Type Optimality Criteria
Before proceeding to the main results of this section, we formulate the following definitions which will be required in the forthcoming analysis:
Definitions: 1) For the functional
the functional 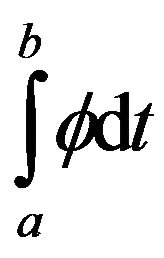 is said to be strict pseudoconvex, if all
is said to be strict pseudoconvex, if all 

Equivalently

2) 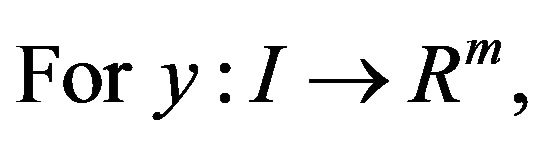 the functional
the functional  is semistrictly pseudoconvex if
is semistrictly pseudoconvex if 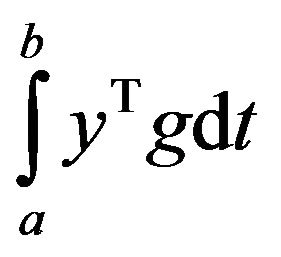 is strictly pseudoconvex for all
is strictly pseudoconvex for all
If 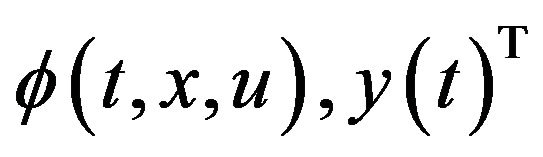 and
and 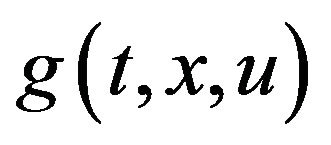 are independent of t and u then the above definitions reduce to those of [6].
are independent of t and u then the above definitions reduce to those of [6].
Theorem 1 (Sufficiency): If  is pseudoconvex,
is pseudoconvex,
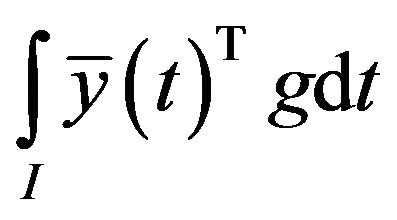 is semi-strictly pseudoconvex and
is semi-strictly pseudoconvex and  is quasiconvex, and if there exist
is quasiconvex, and if there exist
 and piecewise smooth
and piecewise smooth  and
and 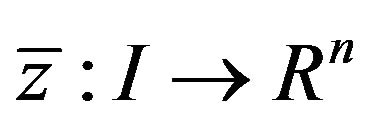 such that from (4)-(8) are satisfied, then
such that from (4)-(8) are satisfied, then 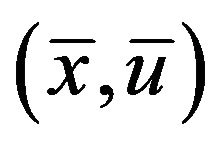 is an optimal solution of (CP).
is an optimal solution of (CP).
Proof: Suppose that  is not optimal for (CP) i.e. there exist
is not optimal for (CP) i.e. there exist  such that
such that

This, by pseudoconvexity of  implies
implies

and
 (9)
(9)
with strict inequality in (9) if .
.
Feasibility of  for (CP) together with (6) implies,
for (CP) together with (6) implies,

which by semi-strict pseudoconvexity of  implies
implies
 (10)
(10)
with strict inequality in (10) if some
 .
.
Also

This, in view of quasiconvexity of 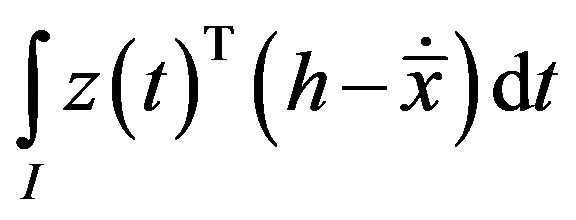 yields
yields

(By integrating by parts)
 (11)
(11)
(Using (1))
Combining (9)-(11), we have

This contradicts (4) and (5). Hence  is an optimal solution of (CP).
is an optimal solution of (CP).
4. Fritz Type Duality
The following is the Fritz john type dual to the problem (CP):
 Maximize
Maximize 
subject to
 (12)
(12)
 (13)
(13)
 (14)
(14)
 (15)
(15)
 (16)
(16)
 (17)
(17)
 (18)
(18)
Theorem 2 (Weak Duality): Assume that
(A1) satisfies  is feasible for (CP) and
is feasible for (CP) and  is feasible for (FrCD).
is feasible for (FrCD).
(A2):  is pseudo-convex,
is pseudo-convex,
 is semi-strictly pseudo-convex and
is semi-strictly pseudo-convex and
 is quasi-convex.
is quasi-convex.
Then

Proof: Suppose
This, because of pseudo-convexity of  yields
yields 
and
 (19)
(19)
with strict inequality in the above with . From the constraints of (CP) and (FrCD), we have
. From the constraints of (CP) and (FrCD), we have

which by semi-strictly pseudo-convexity of
 implying
implying
 (20)
(20)
with strict inequality with ,
,  Also, we have
Also, we have

Using quasi-convexity of 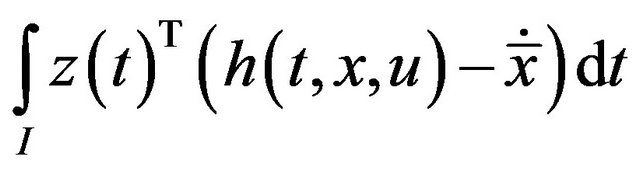 in the above, we have
in the above, we have
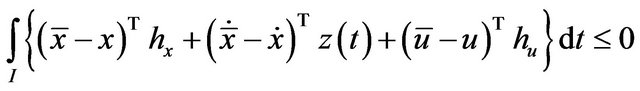 (21)
(21)
which as earlier becomes

Combining (19)-(21), we have
 (22)
(22)
From (13) and (14), we get
 i.e.
i.e.
 (23)
(23)
The relation (22) and (23) are in contradiction, thus

Implying

Theorem 3 (Strong Duality): If is an optimal solution of (CP), then there exist
is an optimal solution of (CP), then there exist  and piecewise smooth
and piecewise smooth  and
and 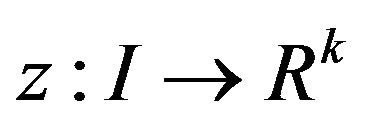 such that
such that 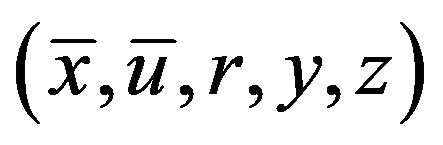 is feasible for (FrCD) and objective values are equal. If hypotheses of Theorem 2 hold, then
is feasible for (FrCD) and objective values are equal. If hypotheses of Theorem 2 hold, then  is an optimal solution of (FrCD).
is an optimal solution of (FrCD).
Proof: Since is an optimal solution of (CP) by Proposition 1, there exist
is an optimal solution of (CP) by Proposition 1, there exist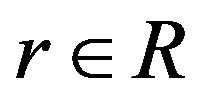 , piecewise smooth
, piecewise smooth  and
and  such that
such that
 (24)
(24)
 (25)
(25)
 (26)
(26)
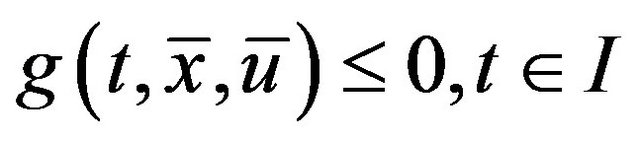 (27)
(27)
 (28)
(28)
 (29)
(29)
 (30)
(30)
The relation (26) implies
 (31)
(31)
and the relation (28) along  gives
gives
 (32)
(32)
The relation (24), (25), (29)-(32), yields the feasibility of 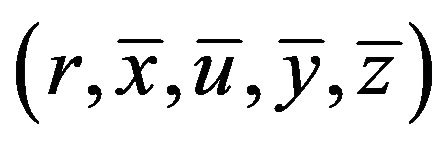 for (FrCD). Equality of objective functionals of (CP) and (FrCD) is obvious from their formulations.
for (FrCD). Equality of objective functionals of (CP) and (FrCD) is obvious from their formulations.
Consequently the optimality for (FrCD) follows, given the pseudo-convexity of the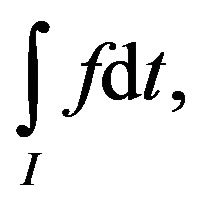 semi-strict pseudoconvexity of
semi-strict pseudoconvexity of  and quasi-convexity of
and quasi-convexity of  by Theorem 2.
by Theorem 2.
Theorem 4 (Strict-Converse duality): Assume that
(A1):  is strictly pseudo-convex,
is strictly pseudo-convex,  is semi-strictly pseudo-convex and
is semi-strictly pseudo-convex and  is quasi-convex.
is quasi-convex.
(A2): 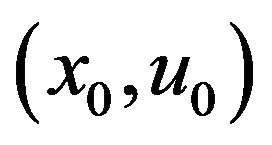 is an optimal solution of (CP) and
is an optimal solution of (CP) and
(A3):  is an optimal solution of (FrCD).
is an optimal solution of (FrCD).
Then  is an optimal solution of (CP) with
is an optimal solution of (CP) with .
.
Proof: we suppose  and exhibit a contradiction. Since
and exhibit a contradiction. Since 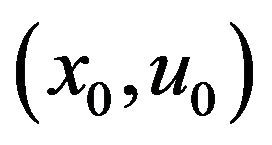 is an optimal solution of (CP) by theorem (Strong Duality) that there exist
is an optimal solution of (CP) by theorem (Strong Duality) that there exist  where
where  and piecewise smooth
and piecewise smooth  and piecewise smooth
and piecewise smooth 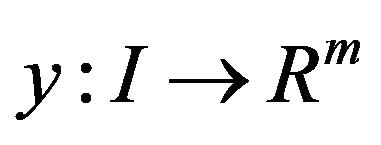 and
and 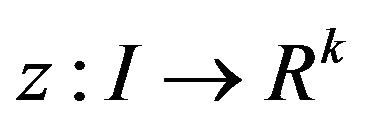 such that
such that  is also an optimal solution for (FrCD), it follows that
is also an optimal solution for (FrCD), it follows that

By strict pseudo-convexity of gives, this implies
gives, this implies

and multiplying the above by 
 (33)
(33)
with strict inequality if  From the constraints of (CP) and (FrCD), we have
From the constraints of (CP) and (FrCD), we have
 (34)
(34)
Also
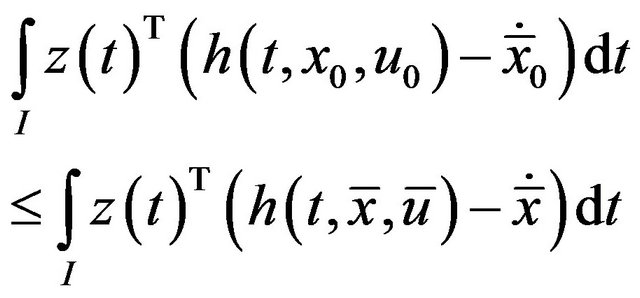 (35)
(35)
By semi-strict pseudoconvexity of and from (34), we have
and from (34), we have
 (36)
(36)
with strict inequality in the above if,

By quasi-convexity of  and from (35), we get
and from (35), we get
 (37)
(37)
As earlier, this reduces to

combining (33), (36), and (37), we have

This contradicts the feasibility of 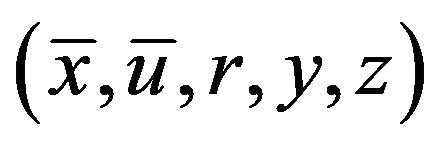 for (FrCD), hence
for (FrCD), hence 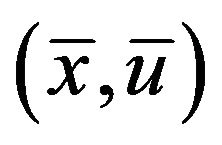 is an optimal solution of (CP) and
is an optimal solution of (CP) and .
.
Theorem 5 (Converse duality): Let  be an optimal solution of (FrCD), Assume
be an optimal solution of (FrCD), Assume
(A1)  is pseudo-convex,
is pseudo-convex,  is semi-strictly pseudo-convex and
is semi-strictly pseudo-convex and  is quasiconvex.
is quasiconvex.
(A2) The set  or
or
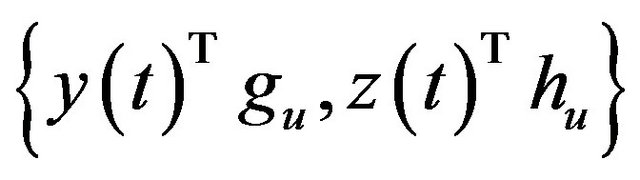 is linearly independent.
is linearly independent.
(A3)  for some column vector
for some column vector 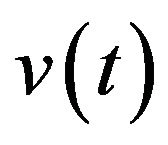 and where
and where

and (A4) 
Then  is optimal for (CP).
is optimal for (CP).
Proof: By Proposition 1, there exist 
 piecewise smooth
piecewise smooth  and
and  such that
such that
 (38)
(38)
 (39)
(39)
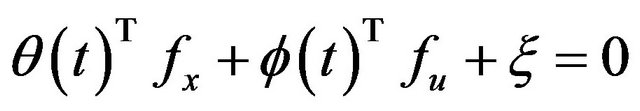 (40)
(40)
 (41)
(41)
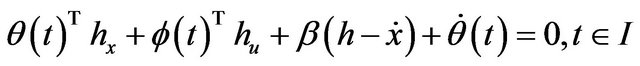 (42)
(42)
 (43)
(43)
 (44)
(44)
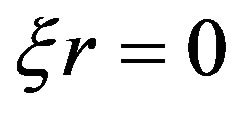 (45)
(45)
 (46)
(46)
 (47)
(47)
 (48)
(48)
Multiplying (41) by 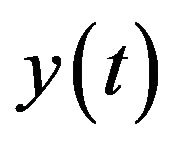 and integrating, and then using (43) and (46), we have
and integrating, and then using (43) and (46), we have

which can be written as
 (49)
(49)
Multiplying (42) by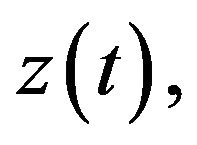 and then integrating we get
and then integrating we get

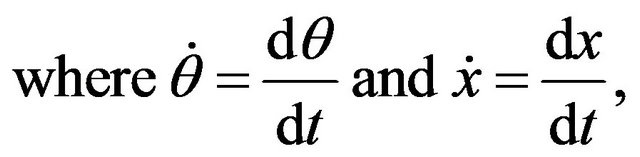 using (44), this yields
using (44), this yields

(by integrating by parts)
which in view of (A4), implies

This can be written as
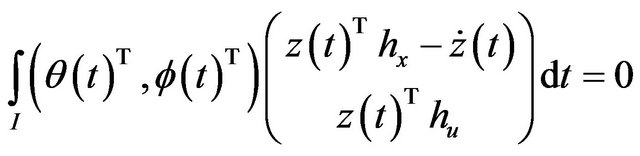 (50)
(50)
Using (13) in (38) and (14) in (39), we have
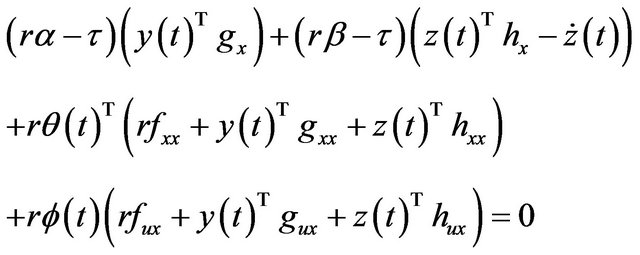
These can be combined as


Pre-multiplying this by  and then integrating we have
and then integrating we have

Using (49) and (50) , this implies

which in view of (A2) implies
 implies
implies
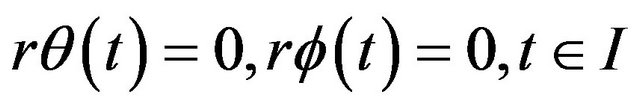 (51)
(51)
In view of (A3), the equality constraint implies  Consequently, we have
Consequently, we have
 (52)
(52)
Using (52), along with , we have
, we have

This, in view of (A3),
 (53)
(53)
If  (53), implies
(53), implies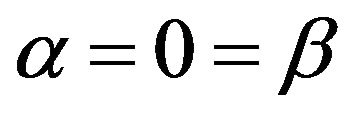 . Thus
. Thus
 contradiction.
contradiction.
Hence  and consequently
and consequently  and
and .
.
From (41) and (42), we have

These relations yield the feasibility of  for (CP) and objective functionals of (CP) and (FrCD) are equal there. Hence under the stated convexity hypotheses, by Theorem 2,
for (CP) and objective functionals of (CP) and (FrCD) are equal there. Hence under the stated convexity hypotheses, by Theorem 2,  is an optimal solution of (CP).
is an optimal solution of (CP).
5. Mathematical Programming Problems
If the problems (CP) and (FrCD) are independent of t and x, these problems reduce to essentially to the static cases of nonlinear programming problem. Letting , the problems (CP) and (FrCD) become the pair of dual nonlinear programming problems formulated by Husain and Srivastav [9].
, the problems (CP) and (FrCD) become the pair of dual nonlinear programming problems formulated by Husain and Srivastav [9].
(CD0): Minimize 
subject to

(FrCD): Maximize 
subject to

where is pseudoconvex,
is pseudoconvex,  is semi-strictly pseudoconvex and
is semi-strictly pseudoconvex and  is quasi-convex. If only inequality constraint in (CD0) is given, then (CP0) and (FrCD0) become a pair of dual the nonlinear programming problems considered by Weir and Mond [10].
is quasi-convex. If only inequality constraint in (CD0) is given, then (CP0) and (FrCD0) become a pair of dual the nonlinear programming problems considered by Weir and Mond [10].
6. Conclusion
In this paper, sufficient optimality conditions are derived for a control problem which appears in various real life situations under generalized convexity assumptions. In order to formulate the dual to this control problem, Fritz John optimality conditions are used instead of KarushKuhn-Tucker optimality condition and hence the requirement of regularity condition is eliminated. Various duality results are obtained and the linkage of our duality results to those of a nonlinear programming problem is indicated. Our results can be seen in the setting of multiobjective control problems.
7. Acknowledgements
The authors acknowledge anonymous referees for their valuable comments which have improved the presentation of this research paper.