Rapid Transport of Biomolecules along Frictionless Wavy-Rough Interfaces ()
1. Introduction
The discovery of water channel proteins, termed aquaporins, has revealed the molecular basis for understanding fluid absorption and secretion through cell membranes in response to even very small osmotic gradients created by solute movement [1,2]. Aquaporins form water channels that play major roles in a variety of physiological processes so that altered expression or function may underlie pathological conditions [3-5]. Note that water transport across the cell membrane is essential for the maintenance of the intracellular environment. Physiological evidence has shown that water molecules move through a selective pore. Despite some qualitative similarities in fluid behavior in cylindrical and slit-like pores, the transport of fluids in confined nanodomains is different in important details, especially for narrow pores [6]. Thus, the boundary conditions for the microscopic domain must be well prescribed!
One prominent difference between the fluid motions in microscale tubes and those in macroscale tubes is the strong fluid-wall interactions observed in microdomains and nanodomains. As the tube size decreases, the surface-to-volume ratio increases. Therefore, various properties of the walls or interfaces, such as surface roughness, greatly affect the fluid motions in microdomains and nanodomains. Although laminar flows have been known to be only slightly influenced by surface roughness in macroscale tubes [7], the effect of surface roughness is expected to be significant in microtubes and nanotubes. Indeed, the amplitude of surface roughness is only one or two orders of magnitude lower than the channel height for many microtubes. In this paper, we shall adopt the verified transition-state or absolute-reaction approach [8,9] which was confirmed [10] that this model developed originally by Eyring [8] can be used to describe fluid flows on the nanoscale. To consider the more realistic but complicated boundary conditions in the walls or interfaces of microdomians and nanodomains (which could be a basic element of a bio-membrane); however, we will use the boundary perturbation technique [7,9] to handle the presumed (approximately) wavyroughness along the walls or interfaces of nanotubes. The relevant boundary conditions [11,12] along the wavyrough surface will be prescribed below after we introduce the Eyring’s model [8,13].
2. Theoretical Formulations
Generally, aquaporins facilitate the movement of water across cell membranes in response to osmotic gradients, functioning in cellular and organismal osmoregulation and solute transport [14,15]. Recent high-resolution structures (via electron and X-ray crystallography) suggest that selectivity for water is accomplished by a filter that excludes larger molecules and a hydrophobic entrance to the pore that blocks the passage of hydrated ions [16-18]. Electrostatic interactions between highly conserved asparagine residues and water molecules in the pore disrupt the hydrogen bonding pattern that would be formed by the chain of water molecules, thereby preventing the conduction of protons [17]. The unusual combination of a hydrophobic pore and a small number of solute binding sites was proposed to facilitate water transport [18]. With above knowledge, we shall borrow and introduce the Eyring’s approach.
Eyring derived a hyperbolic sine relation between the shear rate 
and the shear stress 
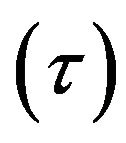[8,13] with sound physical foundation from the thermal activation process [8,9,10,13].
This polymeric fluid is associated with the momentum transfer between neighboring atomic clusters on the microscopic scale and reveals the atomic interaction in the relaxation of viscous flow. It is worth pointing out that the Eyring fluid requires the interaction between atoms in the direction perpendicular to the shearing direction for the momentum transfer. The momentum transfer depends on the activation shear volume, which is associated with the center distance between atoms and is proportional to 
(kB is the Boltzmann constant, T is the temperature in Kelvin, and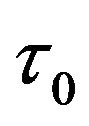 
a constant with the dimension of stress).
We consider a steady fully developed flow of the polymeric fluid in a wavy-rough microtube of a in meanaveraged radius and the outer wall being a fixed wavyrough surface, r = a + εsin(kθ) where (r, θ) is the cylindrical coordinate we adopt, ε is (peak) amplitude of the (wavy) roughness, and k is the wave number (cf. Figure 1).
Firstly, the polymeric fluid can be expressed as [8,9]
(1)
with the forcing parameter
(2)
where
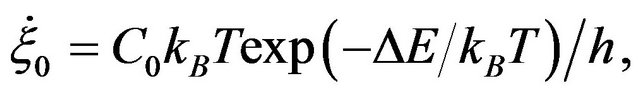(3)
with C0: a constant relating rate of strain to the jump frequency, accounting for the interchain co-operation required; ∆E is the activation energy, h is the Planck constant, 
(=2kBT/Vh) is functions of temperature
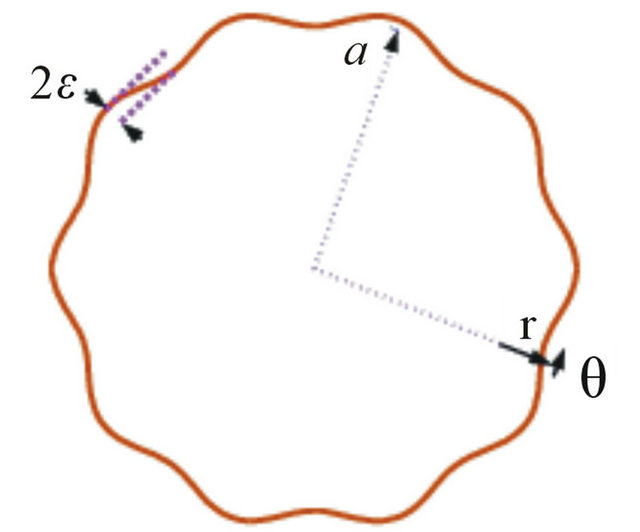
Figure 1. Schematic of a microtube with wavy-rough wall. ε is the amplitude of the roughness and the wave number of wavy roughness is k (=10).
and have the same dimension as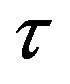
; dp/dz is the pressure-gradient along the microtube-axis direction (z) (for small shear stress
, 
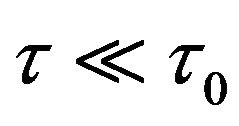represents the viscosity of the material). Note that Vh = ll2l3 is the activation volume for the molecular event [8,9] with l being the average distance between equilibrium positions in the direction of motion, l2 being the distance between neighboring molecules in this same direction (which may or may not equal l), l3 being the molecule to molecule distance in the plane normal to the direction of motion (cf. Figure 2) [8].
Slip Velocity
As 
= −du/dr (u is the velocity of the fluid flow in the longitudinal (z-)direction of the microtube), after integration, we obtain
(4)
here, us ≡ uslip is the velocity over the surface of the microtube [11], which is determined by the boundary condition [7]. We noticed that a general slip boundary condition for transport over a solid surface was proposed [12] as
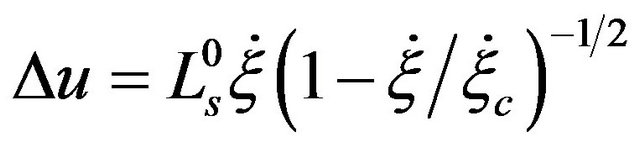, (5)
where ∆u is the velocity jump over the boundary (solid) surface, 
is a constant slip length, 
is the critical shear rate at which the slip length diverges. With the boundary condition from [9,12], we shall derive the velocity field and volume flow rate along the wavy-rough microtube below using the boundary perturbation technique [7,9].
We firstly select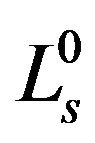 
to be the characteristic length scale and set
. After this, for simplicity, we drop all the primes. It means, from now on, r, z, R0, and ε become dimensionless. Along the boundary, we have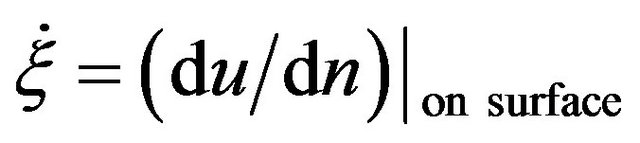
. Here, n means the normal.
Let u be expanded in ε:
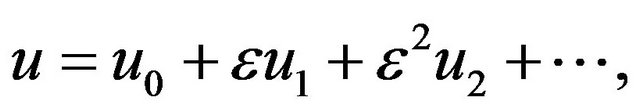(6)
and on the boundary, we expand u(R0 + εdr, θ(=θ0)) into
Figure 2. Schematic model of transport in a polymeric fluid (composed of composite biomolecules) [8,13]. Under an applied force (f) of sufficient magnitude a kink in the composite particles will overcome the activation barrier and jump to an available hole (at A or B).
(7)
where
, (8)
and
.
Now, on the wall (for
), we have [7,9]
(9)
From above equations, we can obtain the velocity fields (up to the second order) and then we can integrate them with respect to the cross-section to get the volume flow rate Q ≡ Qrough = Qsmooth + ε2Q2 up to the second order here.
3. Numerical Results and Discussion
The following figures are for our primary interest: Higher flux or lower resistance (viscosity) which means rather low resistance of the pressure-driven transport of many biomolecules. This can be understood from the net transport Q (µsinhΠ). We have the average velocity: v = Q/Am with Am being the effective area. After this, we then have the flux: rv = |J| which is proportional to the inverse of the flow resistance. The latter is directly relevant to the frictional resistance or shear stress along the tube wall considering the balancing of the driven pressure force when the transport is finally steady or fully developed. This can be evidenced easily once Π is small then we have v µ sinhΠ µ Π µ |dp/dz|.
With the Eyring’s transition-state model [8,13] (of stress-biased thermal activation), structural rearrangement is associated with a single energy barrier (height) 
that is lowered or raised linearly by a (shear) yield stress
. If the transition rate is proportional to the shear strain rate (with a constant ratio: 
≈ 2Vh/Vm), we can calculate the shear stress
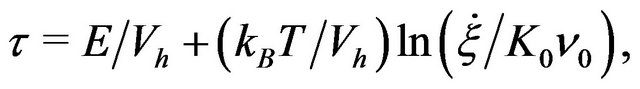(10)
with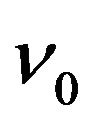 
is an attempt frequency [8,13].
Figure 3 shows that when the shear strain rate (
) is of the order of magnitude O (103 s−1) there are possible frictionless states for pressure driven many-biomolecule flows at the room temperature regime (Tc ~ 300 K). Here a = r2 = 0.1 μm and ε = 0.1. The activation energy is 9 ´ 10−20 Joule and the activation volume is 3.12 ´ 10−21 m3 (T ~ 300 K). We can observe that there is a sharp decrease of shear stress (or resistance) starting from around T ~ 300.5 K. Below around 300 K, the pressure driven transport of many biomolecules is nearly frictionless.
Possible explanation for this almost frictionless transport could be due to the tunneling as the shear thinning removes the barriers. It might be understood that the creation of a large amount of free volume (voids or
Figure 3. Calculated (shear) stresses or resistance using an activation energy 9 ´ 10−20 J. There is a sharp decrease of shear stress starting from around T ~ 300 K. Below around 300 K, the pressure driven transport of many biomolecules is nearly frictionless where the shear strain rate (
) is of the order of the magnitude O (103 s−1).
holes) reduces the barrier for biomolecules or holes to move; i.e., it enhances the mobility of the biomolecules or holes. We remind the readers that aquaporins are members of the Major Intrinsic Protein (MIP) superfamily, found in animals, plants, insects, and bacteria [19-24]. To be specific, aquaporin-mediated water transport across cellular membranes is an ancient, ubiquitous mechanism within cell biology. This family of integral membrane proteins includes both water selective pores (aquaporins) and transport facilitators of other small molecules such as glycerol and urea (aquaglyceroporins).
Eukaryotic aquaporins are frequently regulated posttranslationally by gating, whereby the rate of flux through the channel is controlled, or by trafficking, whereby aquaporins are shuttled from intracellular storage sites to the plasma membrane [25]. With present approach and numerical calculations, we can apply them to the diverse fields of researches related to aquaporins or MIPs in the future [26-29].
4. Conclusion
In brief summary, we have numerically obtained the possible rapid transport (up to the second order) inside the wavy-rough microconduits by using the boundary perturbation method and demonstrated the possible very-low resistance state via the tuning of the activation energy and volume at room temperature regime. Our theoretical results show that for smaller forcing (along the microtube-axis direction; relative to the referenced shear stress), there are significantly different flow rates for different amplitudes of wavy-rough microconduits. The latter result could be directly applied to the efficient biomolecular sieving and separation. Our results should be useful to the design of microfiltration devices (using microtube networks and assemblies), flow control in microfluidics, and other similar applications in biophysics and biochemistry researches. Our next goal is to design and achieve a generic molecular sieving structure for an integrated biomolecule sample preparation and analysis system.
5. Acknowledgements
The only author would like to thank the partial support of 2013—Inner Mongolia University of Science and Technology—Starting Funds for Scientific Researcher. The only author will be at: 2/F, 24, Lane 260, Section 1, Road Muja, Taipei, Taiwan 116, China after 2013-June.