1. Introduction
A semihyperring is essentially a semiring in which addition is a hyperoperation [1]. Semihyperring is in active research for a long time. Vougiouklis [2] generalize the concept of hyperring  by dropping the reproduction axiom where
by dropping the reproduction axiom where  and
and  are associative hyper operations and
are associative hyper operations and  distributes over
distributes over  and named it as semihyperring. Chaopraknoi, Hobuntud and Pianskool [3] studied semihyperring with zero. Davvaz and Poursalavati [4] introduced the matrix representation of polygroups over hyperring and also over semihyperring. Semihyperring and its ideals are studied by Ameri and Hedayati [5].
and named it as semihyperring. Chaopraknoi, Hobuntud and Pianskool [3] studied semihyperring with zero. Davvaz and Poursalavati [4] introduced the matrix representation of polygroups over hyperring and also over semihyperring. Semihyperring and its ideals are studied by Ameri and Hedayati [5].
Zadeh [6] introduced the notion of a fuzzy set that is used to formulate some of the basic concepts of algebra. It is extended to fuzzy hyperstructures, nowadays fuzzy hyperstructure is a fascinating research area. Davvaz introduced the notion of fuzzy subhypergroups in [7], Ameri and Nozari [8] introduced fuzzy regular relations and fuzzy strongly regular relations of fuzzy hyperalgebras and also established a connection between fuzzy hyperalgebras and algebras. Fuzzy subhypergroup is also studied by Cristea [9]. Fuzzy hyperideals of semihyperrings are studied by [1,10,11].
The generalization of Krasner hyperring is introduced by Mirvakili and Davvaz [12] that is named as Krasner (m, n) hyperring. In [13] Davvaz studied the fuzzy hyperideals of the Krasner (m, n)-hyperring. Generalization of hyperstructures are also studied by [1,14-16].
In this paper, we introduce the notion of the generalization of usual semihyperring and called it as (m, n)- semihyperring and set fourth some of its properties, we also introduce fuzzy (m, n)-semihyperring and its basic properties and the relation between fuzzy (m, n)-semihyperring and its associated (m, n)-semihyperring.
The paper is arranged in the following fashion:
Section 2 describes the notations used and the general conventions followed. Section 3 deals with the definitions of (m, n)-semihyperring, weak distributive (m, n)- semihyperring, hyperadditive and multiplicative identity elements, zero, zero sum free, additively idempotent and some examples of (m, n)-semihyperrings.
Section 4 describes the properties of (m, n)-semihyperring. This section deals with the definitions of hyperideals, homomorphism, congruence relation, quotient of (m, n)-semihyperring and also the theorems based on these definitions.
Section 5 deals with the fuzzy (m, n)-semihyperrings, fuzzy hyperideals and homomorphism theorems on (m, n)- semihyperrings and fuzzy (m, n)-semihyperrings.
2. Preliminaries
Let  be a non-empty set and
be a non-empty set and  be the set of all non-empty subsets of
be the set of all non-empty subsets of . A hyperoperation on
. A hyperoperation on 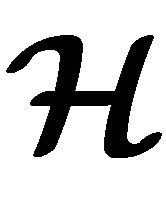 is a map
is a map 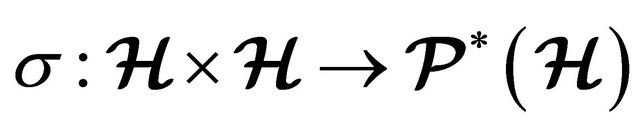 and the couple
and the couple  is called a hypergroupoid. If A and B are non-empty subsets of
is called a hypergroupoid. If A and B are non-empty subsets of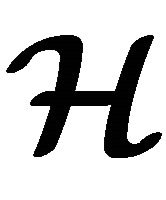 , then we denote
, then we denote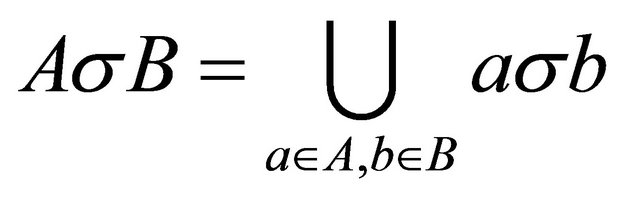 ,
,
 and
and .
.
Let  be a non-empty set,
be a non-empty set,  be the set of all nonempty subsets of
be the set of all nonempty subsets of  and a mapping
and a mapping  is called an m-ary hyperoperation and m is called the arity of hyperoperation [14].
is called an m-ary hyperoperation and m is called the arity of hyperoperation [14].
A hypergroupoid 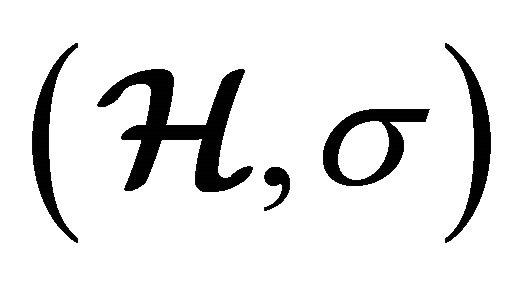 is called a semihypergroup if for all
is called a semihypergroup if for all  we have
we have  which means that
which means that

Let f be an m-ary hyperoperation on 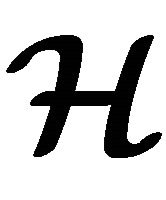 and
and  subsets of
subsets of . We define
. We define

for all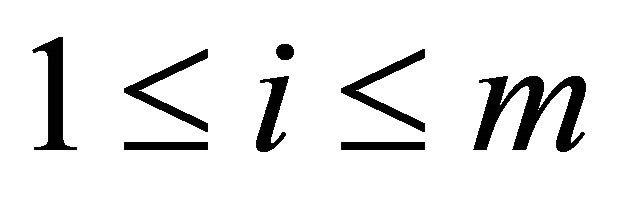 .
.
Definition 2.1  is a semihyperring which satisfies the following axioms:
is a semihyperring which satisfies the following axioms:
1)  is a semihypergroup;
is a semihypergroup;
2)  is a semigroup and;
is a semigroup and;
3)  distributes over
distributes over ,
,
 and
and
 for all
for all  [3].
[3].
Example 2.2 Let  be a semiring, we define
be a semiring, we define
1) 
2) 
Then  is a semihyperring.
is a semihyperring.
An element 0 of a semihyperring  is called a zero of
is called a zero of  if
if  and
and  [3].
[3].
The set of integers is denoted by , with
, with 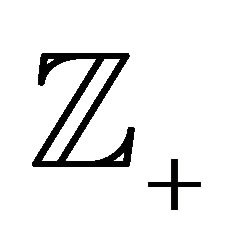 and
and 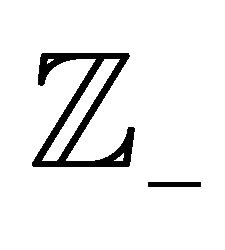 denoting the sets of positive integers and negative integers respectively. Elements of the set
denoting the sets of positive integers and negative integers respectively. Elements of the set  are denoted by
are denoted by 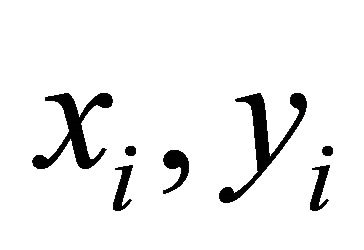 where
where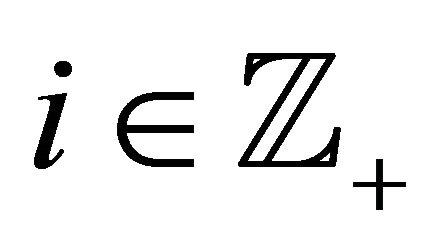 .
.
We use following general convention as followed by [10,17-19]:
The sequence 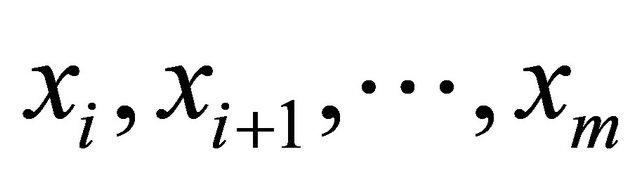 is denoted by
is denoted by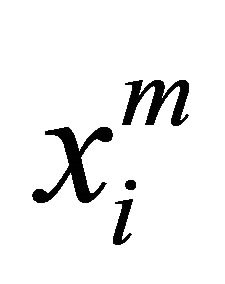 .
.
The following term:
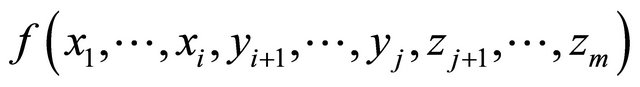 (1)
(1)
is represented as:
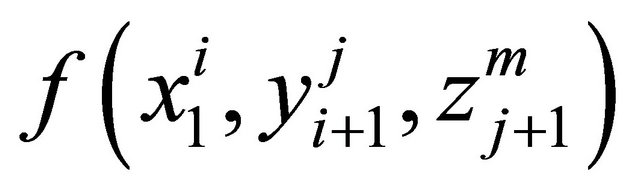 (2)
(2)
In the case when , then (2) is expressed as:
, then (2) is expressed as:

Definition 2.3 A non-empty set 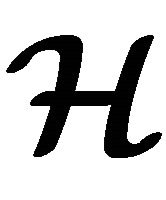 with an m-ary hyperoperation
with an m-ary hyperoperation 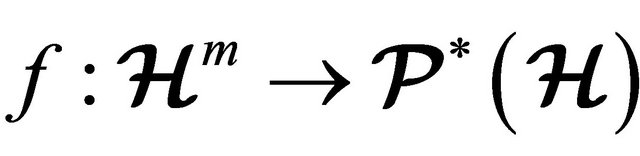 is called an m-ary hypergroupoid and is denoted as
is called an m-ary hypergroupoid and is denoted as . An m-ary hypergroupoid
. An m-ary hypergroupoid  is called an m-ary semihypergroup if and only if the following associative axiom holds:
is called an m-ary semihypergroup if and only if the following associative axiom holds:

for all  and
and 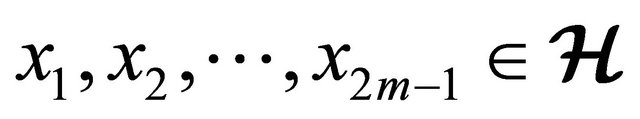 [14].
[14].
Definition 2.4 Element e is called identity element of hypergroup  if
if

for all 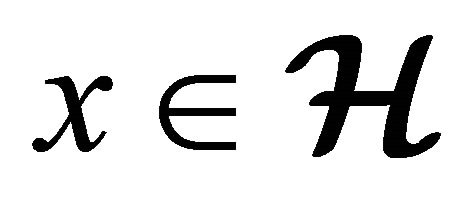 and
and  [14].
[14].
Definition 2.5 A non-empty set 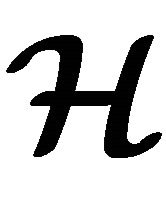 with an n-ary operation g is called an n-ary groupoid and is denoted by
with an n-ary operation g is called an n-ary groupoid and is denoted by  [19].
[19].
Definition 2.6 An  -ary groupoid
-ary groupoid  is called an n-ary semigroup if g is associative, i.e.,
is called an n-ary semigroup if g is associative, i.e.,

for all  and
and  [19].
[19].
3. Definitions and Examples of (m, n)-Semihyperring
Definition 3.1  is an (m, n)-semihyperring which satisfies the following axioms:
is an (m, n)-semihyperring which satisfies the following axioms:
1) 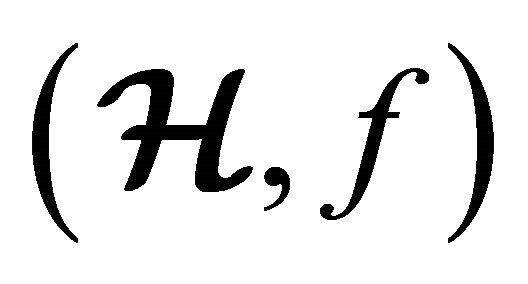 is a m-ary semihypergroup;
is a m-ary semihypergroup;
2) 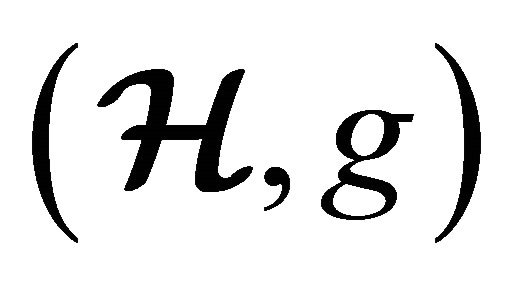 is an n-ary semigroup;
is an n-ary semigroup;
3)  is distributive over f i.e.,
is distributive over f i.e.,

Remark 3.2 An (m, n)-semihyperring is called weak distributive if it satisfies Definition 3.1 1), 2) and the following:
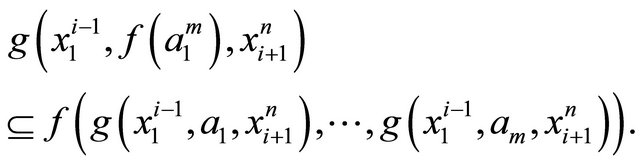
Remark 3.2 is generalization of [20].
Example 3.3 Let 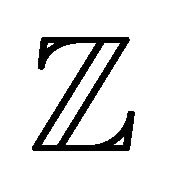 be the set of all integers. Let the binary hyperoperation
be the set of all integers. Let the binary hyperoperation  and an n-ary operation g on
and an n-ary operation g on  which are defined as follows:
which are defined as follows:

and
 .
.
Then  is called a
is called a  -semihyperring.
-semihyperring.
Example 3.3 is generalization of Example 1 of [1].
Definition 3.4 Let e be the hyper additive identity element of hyperoperation f and 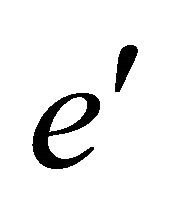 be multiplicative identity element of operation g then
be multiplicative identity element of operation g then
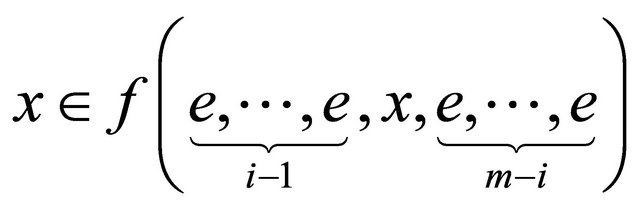
for all 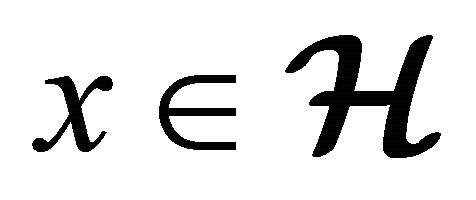 and
and 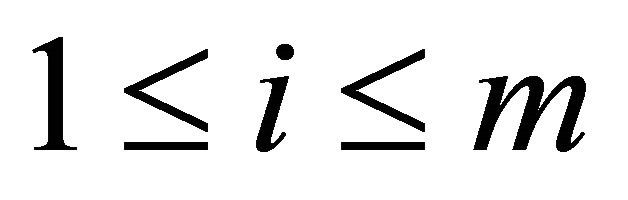 and
and
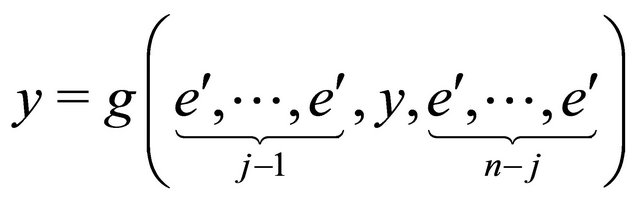
for all  and
and .
.
Definition 3.5 An element 0 of an (m, n)-semihyperring  is called a zero of
is called a zero of  if
if

for all .
.

for all .
.
Remark 3.6 Let  be an (m, n)-semihyperring and e and
be an (m, n)-semihyperring and e and  be hyper additive identity and multiplicative identity elements respectively, then we can obtain the additive hyper operation and multiplication as follows:
be hyper additive identity and multiplicative identity elements respectively, then we can obtain the additive hyper operation and multiplication as follows:

and  for all
for all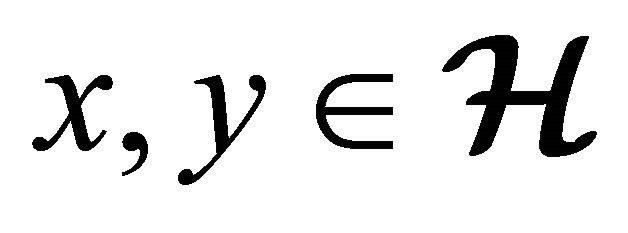 .
.
Definition 3.7 Let  be an (m, n)-semihyperring.
be an (m, n)-semihyperring.
1) (m, n)-semihyperring  is called zero sum free if and only if
is called zero sum free if and only if  implies
implies  .
.
2) (m, n)-semihyperring  is called additively idempotent if
is called additively idempotent if 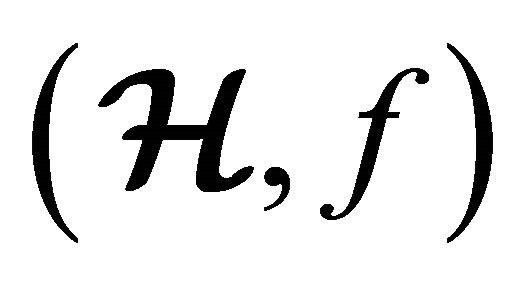 be a m-ary semihypergroup, i.e. if
be a m-ary semihypergroup, i.e. if .
.
4. Properties of (m, n)-Semihyperring
Definition 4.1 Let  be an (m, n)-semihyperring.
be an (m, n)-semihyperring.
1) An m-ary sub-semihypergroup  of
of 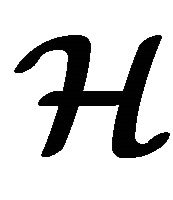 is called an (m, n)-sub-semihyperring of
is called an (m, n)-sub-semihyperring of  if
if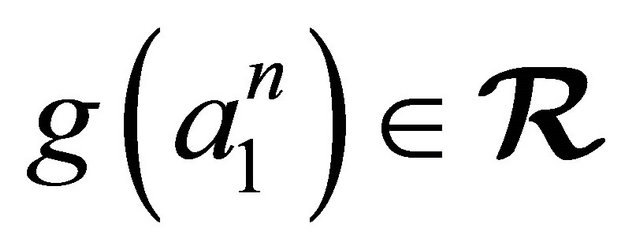 , for all
, for all .
.
2) An m-ary sub-semihypergroup  of
of  is called a) a left hyperideal of
is called a) a left hyperideal of 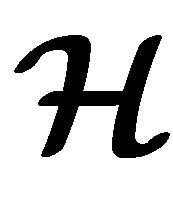 if
if ,
,  and
and .
.
b) a right hyperideal of  if
if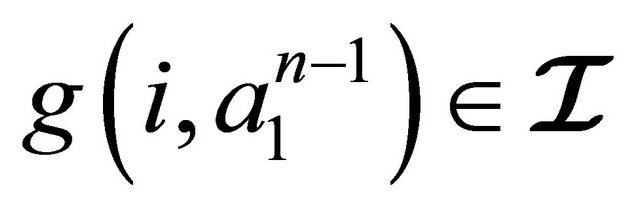 ,
,  and
and .
.
If  is both left and right hyperideal then it is called as an hyperideal of
is both left and right hyperideal then it is called as an hyperideal of .
.
c) a left hyperideal  of an (m, n)-semihyperring of
of an (m, n)-semihyperring of  is called weak left hyperideal of
is called weak left hyperideal of  if for
if for  and
and  then
then 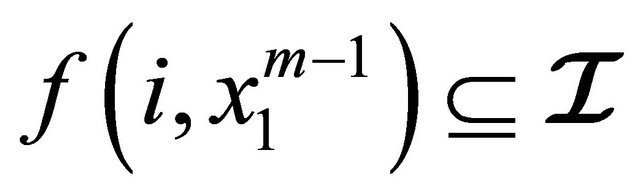 or
or  implies
implies .
.
Definition 4.1 is generalization of [21].
Proposition 4.2 A left hyperideal of an (m, n)-semihyperring is an (m, n)-sub-semihyperring.
Definition 4.3 Let  and
and  be two (m, n)-semihyperrings. The mapping
be two (m, n)-semihyperrings. The mapping  is called a homomorphism if following condition is satisfied for all
is called a homomorphism if following condition is satisfied for all ,
, .
.

and

Remark 4.4 Let  and
and  be two (m, n)-semihyperrings. The mapping
be two (m, n)-semihyperrings. The mapping 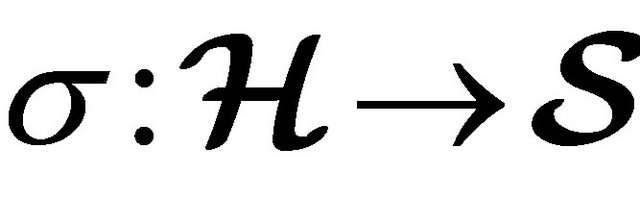 for all
for all ,
, 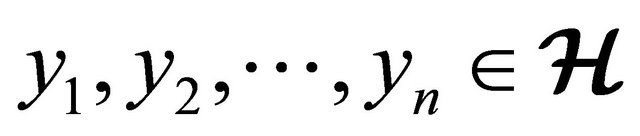 is called an inclusion homomorphism if following relations hold:
is called an inclusion homomorphism if following relations hold:

and

Remark 4.4 is generalization of [7].
Theorem 4.5 Let ,
,  and
and 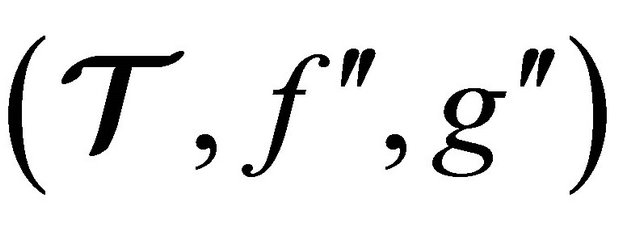 be (m, n)-semihyperrings. If mappings
be (m, n)-semihyperrings. If mappings  and
and  are homomorphisms, then
are homomorphisms, then 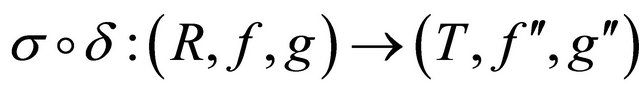 is also a homomorphism.
is also a homomorphism.
Proof. Omitted as obvious.
Definition 4.6 Let 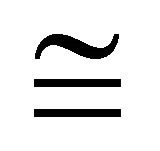 be an equivalence relation on the (m, n)-semihyperring
be an equivalence relation on the (m, n)-semihyperring  and Ai and Bi be the subsets of
and Ai and Bi be the subsets of  for all
for all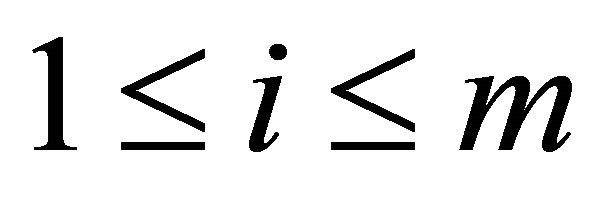 . We define
. We define  for all
for all  there exists
there exists 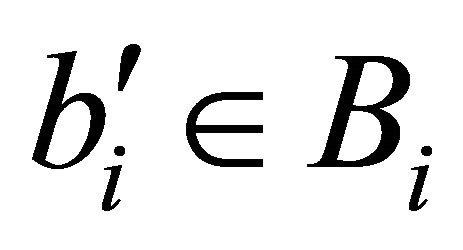 such that
such that  holds true and for all
holds true and for all 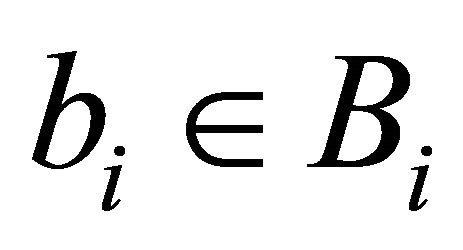 there exists
there exists  such that
such that  holds true [22].
holds true [22].
An equivalence relation  is called a congruence relation on
is called a congruence relation on  if following hold:
if following hold:
1) for all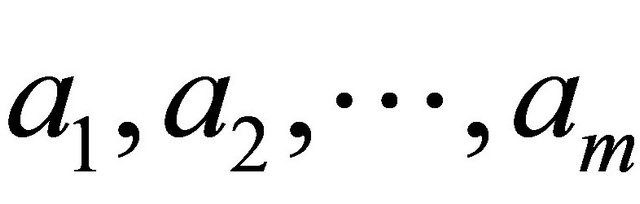 ,
, ; if
; if 
then , where
, where  and2) for all
and2) for all ,
,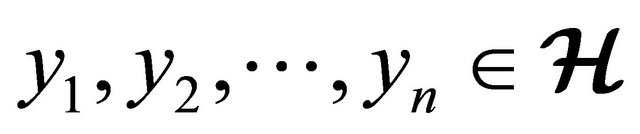 ; if
; if  then
then , where
, where 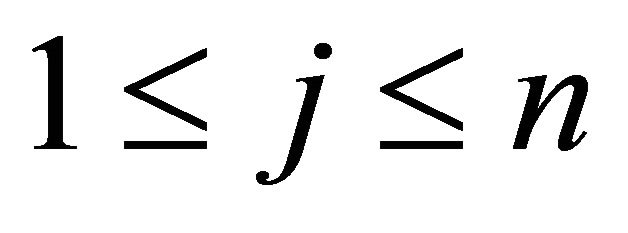 [23].
[23].
Lemma 4.7 Let  be an (m, n)-semihyperring and
be an (m, n)-semihyperring and  be the congruence relation on
be the congruence relation on  then 1) if
then 1) if  then
then

for all 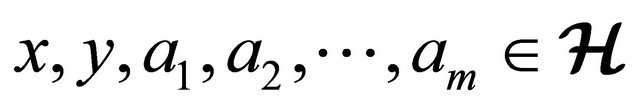
2) if  then following holds:
then following holds:

for all 
Proof.
1) Given that
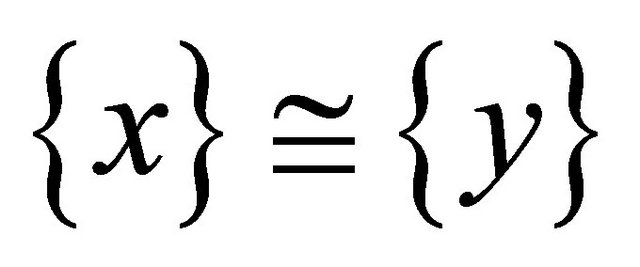 (3)
(3)
for all . Let e be the hyper additive identity element, then (3) can be represented as follows:
. Let e be the hyper additive identity element, then (3) can be represented as follows:
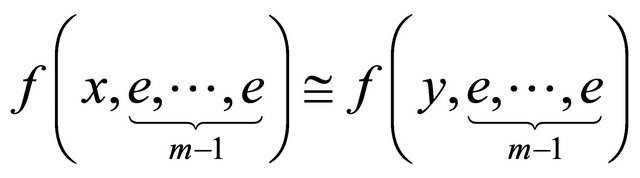 (4)
(4)
do f hyperoperation on both sides of (4) with  to get
to get
 (5)
(5)
 (6)
(6)
 (7)
(7)
do f hyperoperation on both sides of (7) with  to get the following equation:
to get the following equation:
 (8)
(8)
 (9)
(9)
 (10)
(10)
Similarly we can do f hyperoperation till  to get the following result:
to get the following result:
 (11)
(11)
Which can also be represented as:
 (12)
(12)
2) Given that
 (13)
(13)
for all . Let
. Let  be the multiplicative identity element
be the multiplicative identity element
 (14)
(14)
do g hyperoperation on both sides of (14) with  to get
to get
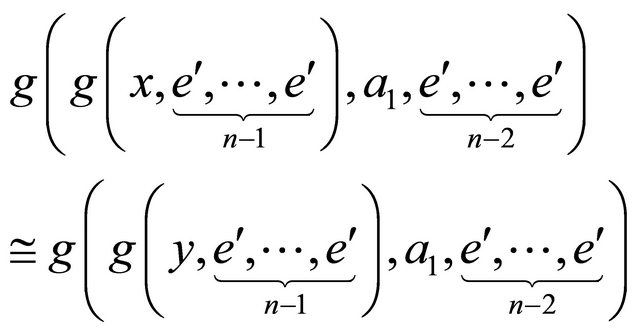 (15)
(15)
 (16)
(16)
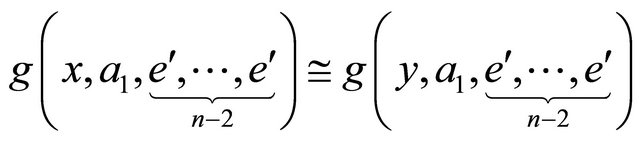 (17)
(17)
do g hyperoperation on both sides of (17) with 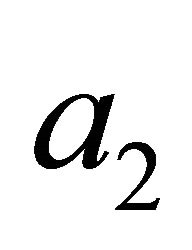 to get the following equation:
to get the following equation:
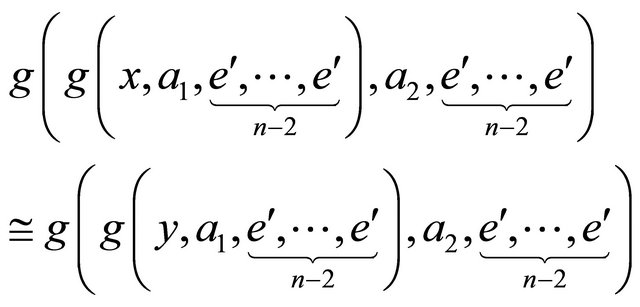 (18)
(18)
 (19)
(19)
 (20)
(20)
Similarly we can do g operation till  to get the following result:
to get the following result:

Theorem 4.8 Let  be an (m, n)-semihyperring and
be an (m, n)-semihyperring and  be the congruence relation on
be the congruence relation on . Then if
. Then if  and
and 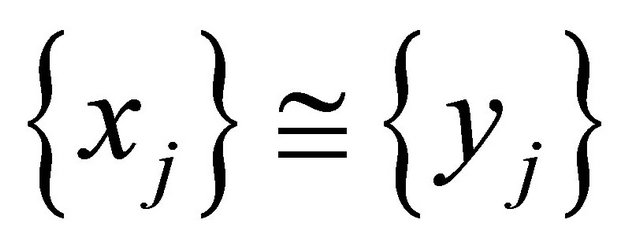 for all
for all 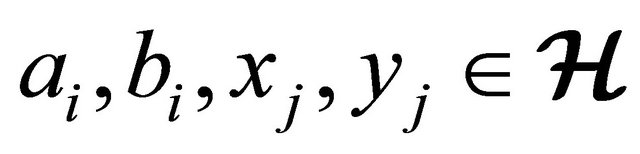 and
and  then the following is obtained: for all
then the following is obtained: for all 

Proof. Can be proved similar to Lemma 4.7.
Definition 4.9 Let  be a congruence on
be a congruence on . Then the quotient of
. Then the quotient of  by
by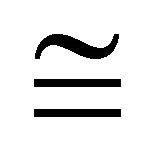 , written as
, written as , is the algebra whose universe is
, is the algebra whose universe is  and whose fundamental operation satisfy
and whose fundamental operation satisfy
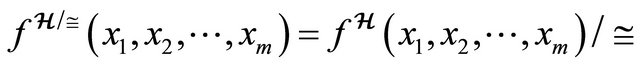
where  [23].
[23].
Theorem 4.10 Let  be an (m, n)-semihyperring and
be an (m, n)-semihyperring and 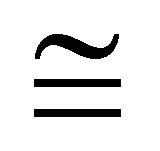 be the equivalence relation and strongly regular on
be the equivalence relation and strongly regular on  then
then  is also an (m, n)-semihyperring.
is also an (m, n)-semihyperring.
Definition 4.11 Let  be an (m, n)-semihyperring and
be an (m, n)-semihyperring and 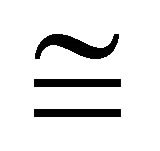 be the congruence relation. The natural map
be the congruence relation. The natural map  is defined by
is defined by 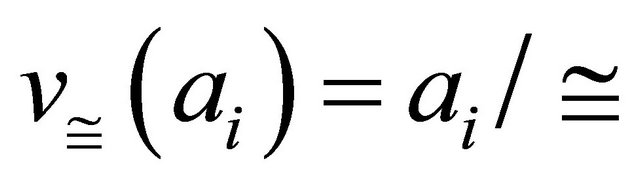 and
and  where
where  for all
for all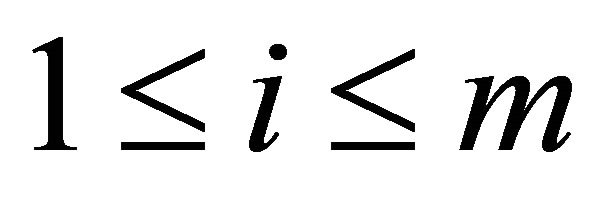 ,
,  .
.
Theorem 4.12 Let  and
and  be two congruence relations on (m, n)-semihyperring
be two congruence relations on (m, n)-semihyperring 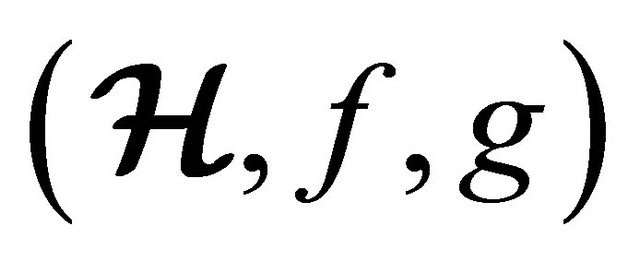 such that
such that . Then
. Then

is a congruence on  and
and 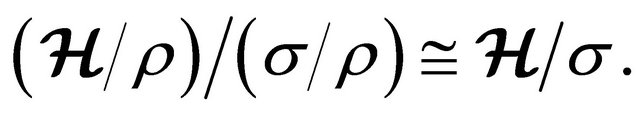
Proof. Similar to [24], we can deduce that  is an equivalence relation on
is an equivalence relation on . Suppose
. Suppose  for all
for all  and
and  for all
for all  . Since
. Since  is congruence on
is congruence on  therefore
therefore  and
and  which implies
which implies
 and
and  respectively, therefore
respectively, therefore  is a congruence on
is a congruence on .
.
Theorem 4.13 The natural map from an (m, n)-semihyperring  to the quotient
to the quotient 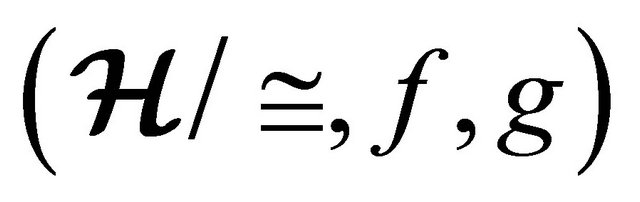 of the (m, n)-semihyperring is an onto homomorphism.
of the (m, n)-semihyperring is an onto homomorphism.
Definition 4.11 and Theorem 4.13 is generalization of [23].
Proof. let  be the congruence relation on (m, n)- semihyperring
be the congruence relation on (m, n)- semihyperring  and the natural map be
and the natural map be  . For all
. For all , where
, where  following holds true:
following holds true:

In a similar fashion we can deduce for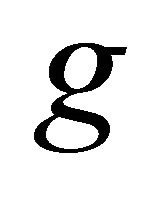 , for all
, for all , where
, where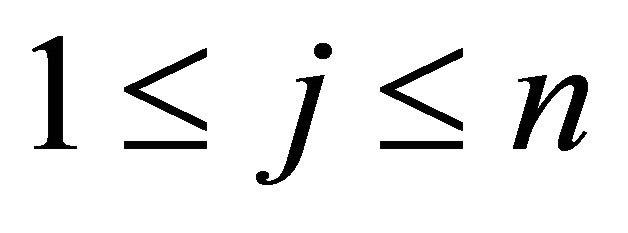 :
:

So 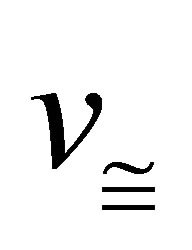 is onto homomorphism.
is onto homomorphism.
Proof is similar to [23].
5. Fuzzy (m, n)-Semihyperring
Let  be a non-empty set. Then 1) A fuzzy subset of
be a non-empty set. Then 1) A fuzzy subset of  is a function
is a function ;
;
2) For a fuzzy subset  of
of  and
and , the set
, the set  is called the level subset of
is called the level subset of  [1,6,13,25].
[1,6,13,25].
Definition 5.1 A fuzzy subset  of an (m, n)-semihyperring
of an (m, n)-semihyperring  is called a fuzzy (m, n)-sub-semihyperring of
is called a fuzzy (m, n)-sub-semihyperring of  if following hold true:
if following hold true:
1) 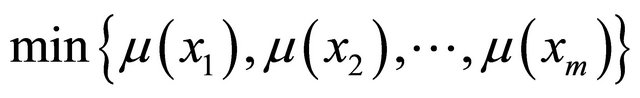
 for all
for all 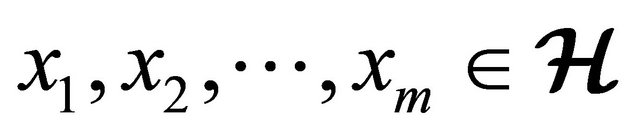
2) 
 for all
for all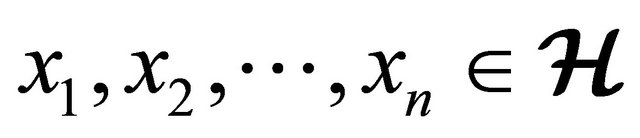 .
.
Definition 5.2 A fuzzy subset  of an (m, n)-semihyperring
of an (m, n)-semihyperring  is called a fuzzy hyperideal of
is called a fuzzy hyperideal of 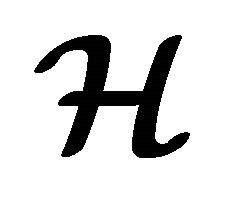 if the following hold true:
if the following hold true:
1) 
 for all
for all 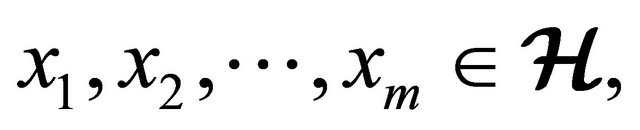
2) , for all
, for all  3)
3) , for all
, for all  ,
,

4) , for all
, for all 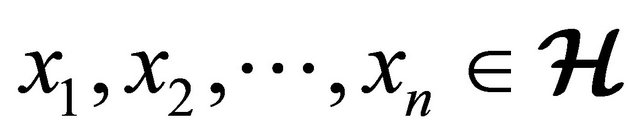 .
.
Theorem 5.3 A fuzzy subset  of an (m, n)-semihyperring
of an (m, n)-semihyperring 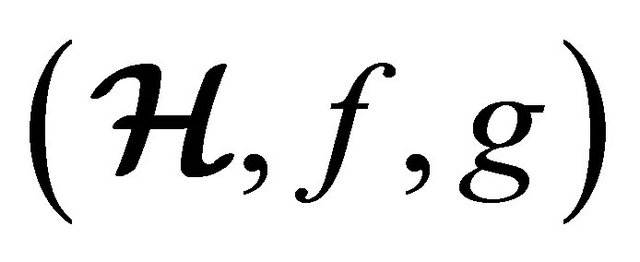 is a fuzzy hyperideal if and only if every non-empty level subset is a hyperideal of
is a fuzzy hyperideal if and only if every non-empty level subset is a hyperideal of .
.
Proof. Suppose subset  is a fuzzy hyperideal of (m, n)-semihyperring
is a fuzzy hyperideal of (m, n)-semihyperring  and
and 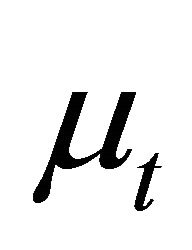 is a level subset of
is a level subset of .
.
If  for some
for some 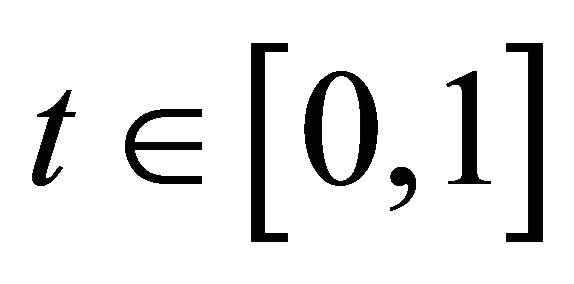 then from the definition of level set, we can deduce the following:
then from the definition of level set, we can deduce the following:

Thus, we say that:

Thus:
 (21)
(21)
So, we get the following:
 , for all
, for all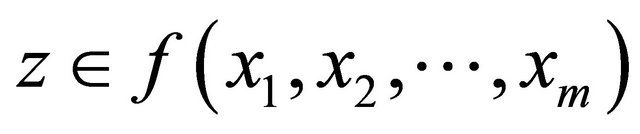 .
.
Therefore, .
.
Again, suppose that  and
and , where
, where . Then, we find that
. Then, we find that .
.
So, we obtain the following:
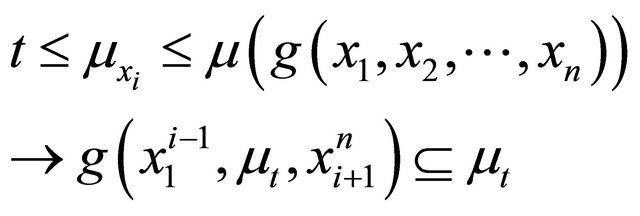 (22)
(22)
Thus, we find that  is a hyperideal of
is a hyperideal of .
.
On the other hand, suppose that every non-empty level subset 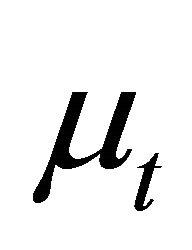 is a hyperideal of
is a hyperideal of .
.
Let , for all
, for all  .
.
Then, we obtain the following:

Thus,

We can also obtain that:

Thus,
 (23)
(23)
Again, suppose that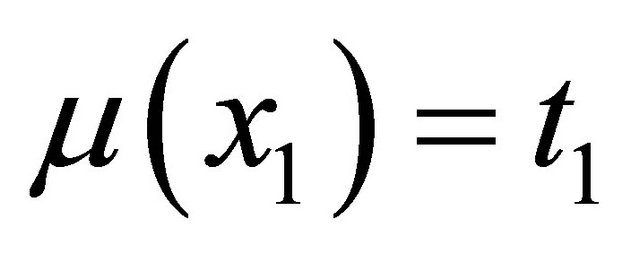 . Then
. Then .
.
So, we obtain:
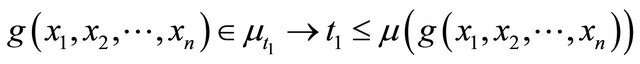
Thus, .
.
Similarly, we obtain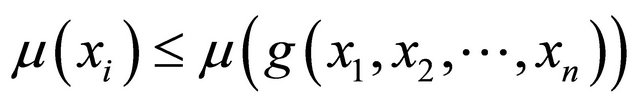 , for all
, for all .
.
Thus, we can check all the conditions of the definition of fuzzy hyperideal.
This proof is a generalization of [1].
Theorem 5.3 is a generalization of [1,11,26].
Jun, Ozturk and Song [27] have proposed a similar theorem on hemiring.
Theorem 5.4 Let 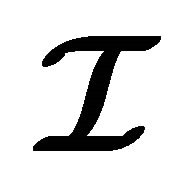 be a non-empty subset of an (m, n)-semihyperring
be a non-empty subset of an (m, n)-semihyperring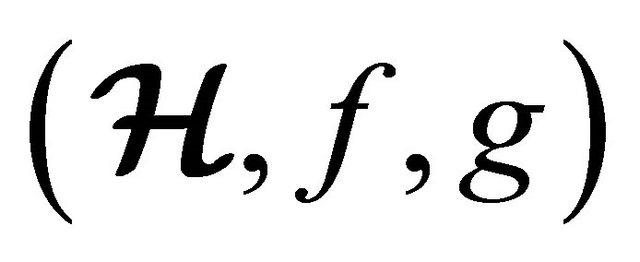 . Let
. Let 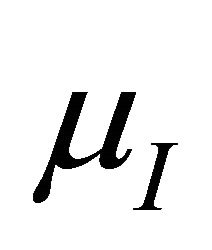 be a fuzzy set defined as follows:
be a fuzzy set defined as follows:

where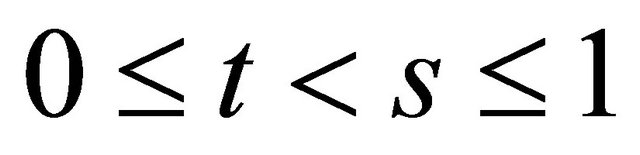 . Then
. Then  is a fuzzy left hyper ideal of
is a fuzzy left hyper ideal of  if and only if
if and only if  is a left hyper ideal of
is a left hyper ideal of .
.
Following Corollary 5.5 is generalization of [1].
Corollary 5.5 Let  be a fuzzy set and its upper bound be
be a fuzzy set and its upper bound be  of an (m, n)-semihyperring
of an (m, n)-semihyperring . Then the following are equivalent:
. Then the following are equivalent:
1)  is a fuzzy hyperideal of
is a fuzzy hyperideal of .
.
2) Every non-empty level subset of  is a hyperideal of
is a hyperideal of .
.
3) Every level subset  is a hyperideal of
is a hyperideal of 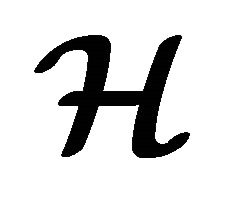 where
where .
.
Definition 5.6 Let 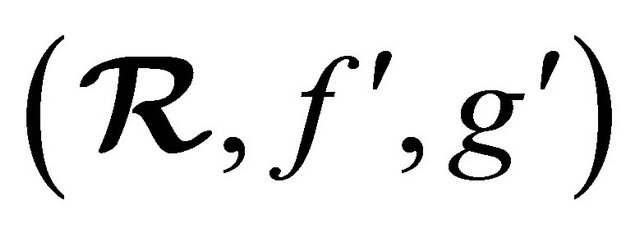 and
and  be fuzzy (m, n)-semihyperrings and
be fuzzy (m, n)-semihyperrings and  be a map from
be a map from  into
into . Then
. Then  is called homomorphism of fuzzy (m, n)- semihyperrings if following hold true:
is called homomorphism of fuzzy (m, n)- semihyperrings if following hold true:

and

for all 
Theorem 5.7 Let  and
and  be two fuzzy (m, n)-semihyperrings and
be two fuzzy (m, n)-semihyperrings and  and
and 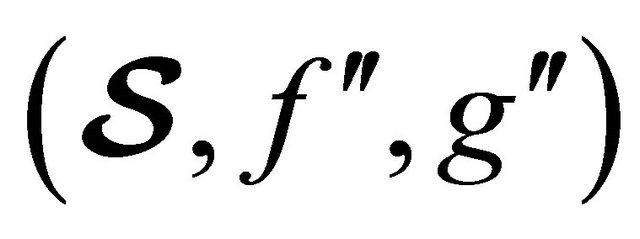 be associated (m, n)-semihyperring. If
be associated (m, n)-semihyperring. If  is a homomorphism of fuzzy (m, n)-semihyperrings, then
is a homomorphism of fuzzy (m, n)-semihyperrings, then  is homomorphism of the associated (m, n)-semihyperrings also.
is homomorphism of the associated (m, n)-semihyperrings also.
Definition 5.6 and Theorem 5.7 are similar to the one proposed by Leoreanu-Fotea [16] on fuzzy (m, n)-ary hyperrings and (m, n)-ary hyperrings and Ameri and Nozari [8] proposed a similar Definition and Theorem on hyperalgebras.
6. Conclusion
We proposed the definition, examples and properties of (m, n)-semihyperring. (m, n)-semihyperring has vast application in many of the computer science areas. It has application in cryptography, optimization theory, fuzzy computation, Baysian networks and Automata theory, listed a few. In this paper we proposed Fuzzy (m, n)- semihyperring which can be applied in different areas of computer science like image processing, artificial intelligence, etc. We found some of the interesting results: the natural map from an (m, n)-semihyperring to the quotient of the (m, n)-semihyperring is an onto homomorphism. It is also found that if 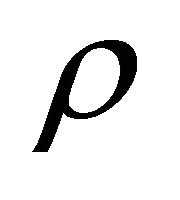 and
and  are two congruence relations on (m, n)-semihyperring
are two congruence relations on (m, n)-semihyperring  such that
such that , then
, then 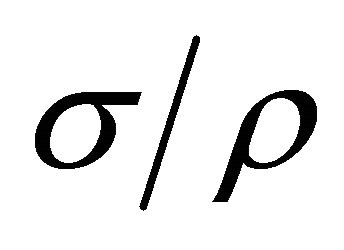 is a congruence on
is a congruence on  and
and  We found many interesting results in fuzzy (m, n)-semihyperring as well, like, a fuzzy subset
We found many interesting results in fuzzy (m, n)-semihyperring as well, like, a fuzzy subset  of an (m, n)-semihyperring
of an (m, n)-semihyperring  is a fuzzy hyperideal if and only if every non-empty level subset is a hyperideal of
is a fuzzy hyperideal if and only if every non-empty level subset is a hyperideal of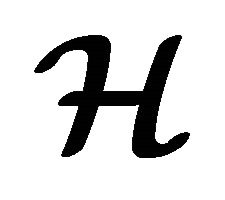 . We can use (m, n)-semihyperring in cryptography in our future work.
. We can use (m, n)-semihyperring in cryptography in our future work.
7. Acknowledgements
The first author is indebted to Prof. Shrisha Rao of IIIT Bangalore for encouraging him to do research in this area. A few basic definitions were presented when the first author was a master’s student under the supervision of Prof. Shrisha Rao at IIIT Bangalore.