Chaotic Fractals at the Root of Relativistic Quantum Physics and Cosmology ()
1. Introduction
The closing report of a notable Nobel conference [1] held in Stockholm in 1984 contained the remarkable and at the time prophetic statement about the role which the science of nonlinear dynamics, chaos and fractals is expected to play in quantum physics. In fact it was stated in clear terms that nonlinear dynamics, chaos and fractals will “invade” the foundations of quantum physics [1,2]. In the present work we will give a short summary of some truly exciting developments confirming the Nobel conference prophecy not only in quantum physics but also in cosmology and specifically in resolving the mystery of the so called missing dark energy of the cosmos [3,4] as well as the fractal meaning of the constancy of the speed of light, negative gravity and negative absolute temperature in Kelvin scale [3-6].
2. Non-Commutative Geometry and Fractal Cantorian Space-Time
Besides M-theory, super strings and loop quantum gravity, A. Connes’ non-commutative geometry is generally accepted as a most promising theory for high energy particle physics and quantum gravity [7]. Vital for understanding this theory is to realize its close connection to chaotic fractals and nonlinear dynamics [7-13]. The simplest way to see that is to start from von Neumann-Connes’ dimensional function and then establish its equivalence to the bijection equation and the formalism of E-infinity Cantorian space-time and Penrose fractal tiling [9- 11]. The said dimensional function is given by [9]
 (1)
(1)
where 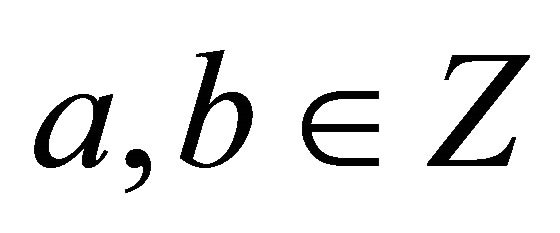 and
and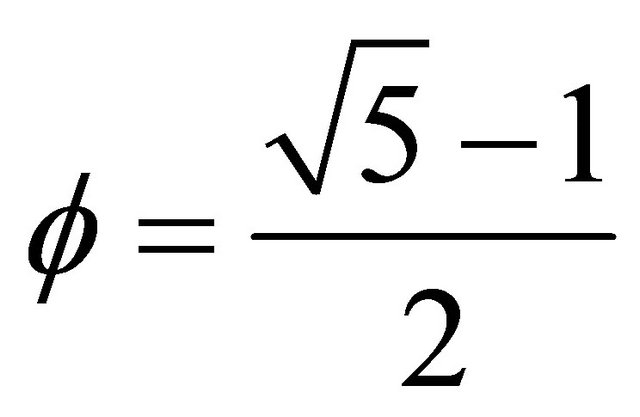 . Starting with the seed
. Starting with the seed
 and
and 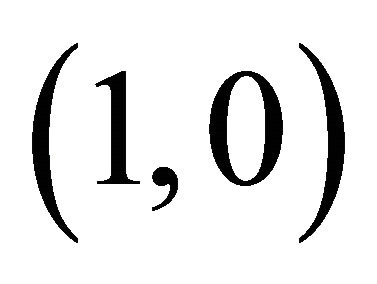 then proceeding in a Fibonacci manner one finds [9]
then proceeding in a Fibonacci manner one finds [9]
 (2)
(2)
and so on.
Proceeding inductively one finds
 (3)
(3)
where a, b represents the classical Fibonacci numbers and consequently moving in the direction of negative Menger-Urysohn dimension one finds [9-11]
 (4)
(4)
Thus
 (5)
(5)
is just another way of writing the bijection formula of Einfinity Cantorian space-time [9-11]
 (6)
(6)
where  is the Hausdorff dimension of a randomly constructed elementary triadic Cantor set, i.e. a chaotic version of the classical triadic set
is the Hausdorff dimension of a randomly constructed elementary triadic Cantor set, i.e. a chaotic version of the classical triadic set  [10,11]. We note the proximity of the magnitude of
[10,11]. We note the proximity of the magnitude of 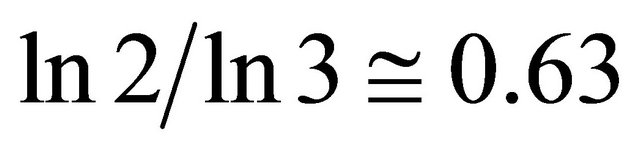 to the golden mean
to the golden mean  [10,11]. Two important results can immediately be established, namely that [7,9-11]
[10,11]. Two important results can immediately be established, namely that [7,9-11]  the Hausdorff dimension of the classical empty set [2,10,11] while
the Hausdorff dimension of the classical empty set [2,10,11] while  is the Hausdorff dimension of the truly empty set [2,10,11].
is the Hausdorff dimension of the truly empty set [2,10,11].
Consequently the distance between  and
and
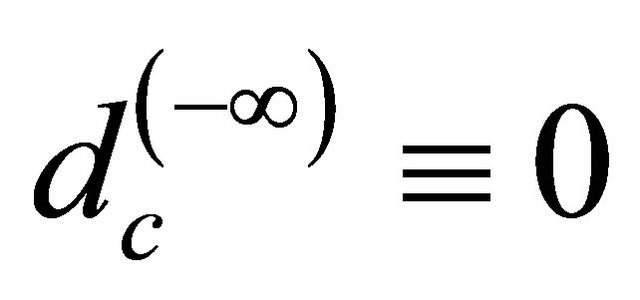 measures the degree of emptiness of an empty Cantor set (dust) [9-11].
measures the degree of emptiness of an empty Cantor set (dust) [9-11].
3. Penrose Quasi-Periodic Fractal Tiling Universe
One of the most fundamental connections between noncommutative geometry and E-infinity theory is undoubtedly the famous Penrose quasi-periodic tiling universe with its golden mean proportionality [9]. It is easy to see the connection to random Cantor sets and the compactified Klein modular curve when realizing the existence of an isomorphic length for this space equal to [9-11]
 (7)
(7)
where  and
and 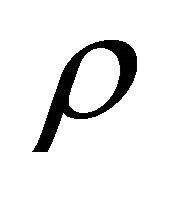 is an arbitrary radius. In other words, latest after moving a distance equal
is an arbitrary radius. In other words, latest after moving a distance equal  the space reproduces itself exactly. This is clearly a universe which is its own multi-verse. We see here how the self-similarity and self-affinity of fractals can solve seemingly and superficial contradictory notions such as whether we live in a multi-verse or a universe.
the space reproduces itself exactly. This is clearly a universe which is its own multi-verse. We see here how the self-similarity and self-affinity of fractals can solve seemingly and superficial contradictory notions such as whether we live in a multi-verse or a universe.
From the above we see that in a fractal universe of the Penrose non-commutative type the problem resolves itself.
4. Quantum Entanglement as a Consequence of a Zero Measure Fractal Geometry
The totally incomprehensive riddle of spatial separation in quantum mechanics may easily be resolved using the property of zero Lebesque measure of all totally disjointed Cantor sets [12,13]. There is irrefutable theoretical and experimental proof for this E-infinity based proposal [12,13]. The story goes as follows: Using an ingenious Gedanken experiment L. Hardy [14] was able to establish via Dirac’s orthodox quantum mechanical computation that the probability for quantum entanglement of two quantum particles is given by . On close examination by first Mermin [15] and then the second author [12], it becomes evident that Hardy rounded off the result concealing its exact numerical magnitude namely that [12,13,15]
. On close examination by first Mermin [15] and then the second author [12], it becomes evident that Hardy rounded off the result concealing its exact numerical magnitude namely that [12,13,15]
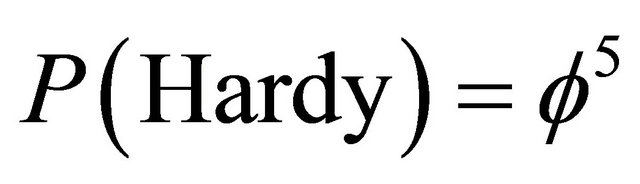 (8)
(8)
where 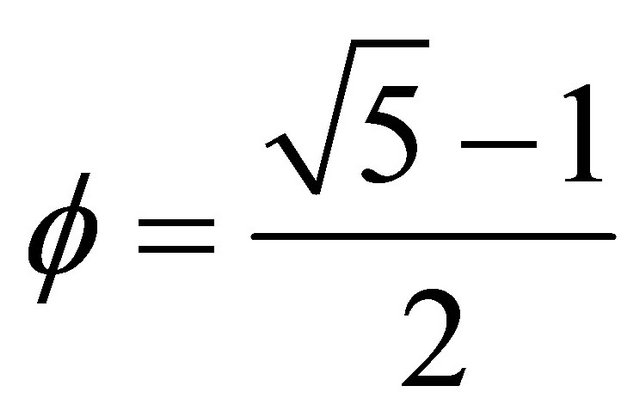 is the golden mean. The E-infinity interpretation stems from the general E-infinity formula for the probability of quantum entanglement [13]
is the golden mean. The E-infinity interpretation stems from the general E-infinity formula for the probability of quantum entanglement [13]
 (9)
(9)
where n is the number of quantum particles and  is the inverse of the Hausdorff dimension of the E-infinity fractal space-time core [10,11]
is the inverse of the Hausdorff dimension of the E-infinity fractal space-time core [10,11]
 (10)
(10)
For two particles this means
 (11)
(11)
Seen that way quantum entanglement can be understood as a natural consequence of the zero length (i.e. zero measure) of a Cantor set and the problem of spatial separation in quantum mechanics is swept away. In a zero measure space-time manifold there is simply no meaning for spatial separation [13]. This incredible result of Hardy-Mermin and El Naschie was experimentally confirmed using various accurate methods in many international laboratories [13-15].
5. The Missing Energy of the Universe
At present the problem, of dark energy or the missing energy in the universe, constitutes the most challenging problem in physics and cosmology alike [3,5,6]. Accurate measurement has shown that only 4.5% of the total energy thought to be contained in the universe is detectable [3,5]. The simple conclusion for these results which were awarded the 2011 Nobel Prize in Physics is that either Einstein’s equation contains some error or 95.5% of the energy in the universe is due to mysterious dark matter and dark energy which cannot be detected with any known methods [3,5,6]. The nonlinear-dynamical fractal resolution of this problem however is unbelievably simple, more than one could imagine [3,5]. The rationale behind this is as follows: If space-time itself is a real Cantorian fractal then it resembles an unimaginably large cotton candy [5,7,11,13]. The majority of this cosmic cotton candy is naturally voids containing nothing, not even space or time. Consequently Einstein’s famous equation [5]
 (12)
(12)
must be modified to take all these fractal voids into consideration. This can be done in various equivalent ways. The simplest is to take bosonic strings compactified “dark” dimensions into account in the form of a Weyl-Nottale scaling factor. Since bosonic string space has 26 dimensions and Einstein’s relativity is only 4 dimensional then the “dark” dimensions are 26 – 4 = 22 and our scaling factor must be [5]
 (13)
(13)
Consequently the revised E is
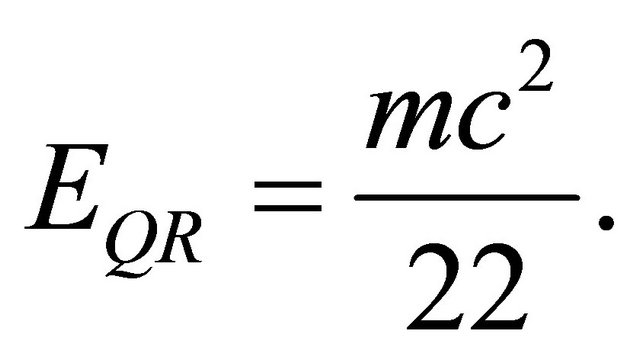 (14)
(14)
Noting that , we see that the new EQR accurately accounts for the cosmological measurements [3].
, we see that the new EQR accurately accounts for the cosmological measurements [3].
Another way to come to the same conclusion is to reason that from high energy particle physics point of view  is based on the existence of one messenger particle, namely the photon
is based on the existence of one messenger particle, namely the photon  However this was in 1905 when Einstein conceived his theory. In the meantime we know that we have 12 messenger photon-like particles given by the Lie symmetry groups of the standard model of particle physics [10,11]
However this was in 1905 when Einstein conceived his theory. In the meantime we know that we have 12 messenger photon-like particles given by the Lie symmetry groups of the standard model of particle physics [10,11]
 . (15)
. (15)
Consequently by inserting  in Newton’s kinetic energy and letting
in Newton’s kinetic energy and letting  one finds
one finds
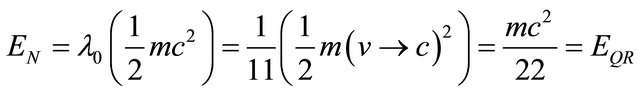 (16)
(16)
exactly as in the first derivation, namely Equation (14).
6. Unifying Relativity and Quantum Theory via Zero Measure Fractals
The previous derivations of the revised Einstein equation
 were only very accurate approximations. However an exact derivation can be obtained when taking the exact fractal nature of quantum entanglement in deriving EQR. Again this could be done in several equivalent ways. Here we give two methods only. The first is based upon formal analogy between the E-formula of the theory of varying speeds of light (see Figure 1) [16,17]
were only very accurate approximations. However an exact derivation can be obtained when taking the exact fractal nature of quantum entanglement in deriving EQR. Again this could be done in several equivalent ways. Here we give two methods only. The first is based upon formal analogy between the E-formula of the theory of varying speeds of light (see Figure 1) [16,17]
 (17)
(17)
and the Cantor set unit interval physics of Ultimate L and F and Taiji-El Naschie theory [18,19] (see Figure 2). Here denotes the Planck energy [15,16]. Now within Taiji-El Naschie theory
denotes the Planck energy [15,16]. Now within Taiji-El Naschie theory  is simply equal to
is simply equal to 
 while the devisor m is the five dimensionality of Kaluza-Klein and similarly the devisor c is Sigalotti’s critical speed [20-22]
while the devisor m is the five dimensionality of Kaluza-Klein and similarly the devisor c is Sigalotti’s critical speed [20-22] . Inserting in E one finds (see Figures 1-3)
. Inserting in E one finds (see Figures 1-3)
 (18)
(18)
In other words the exact  of quantum relativity is equal Einstein
of quantum relativity is equal Einstein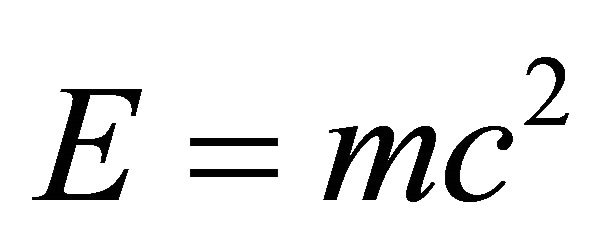 multiplied with half of Hardy’s
multiplied with half of Hardy’s 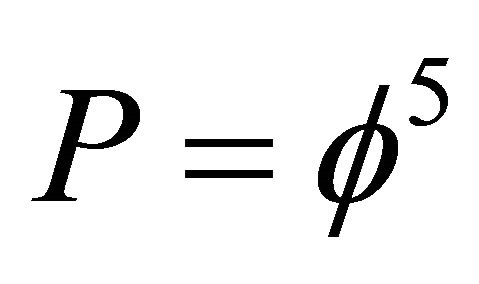 [12-15]. That means
[12-15]. That means
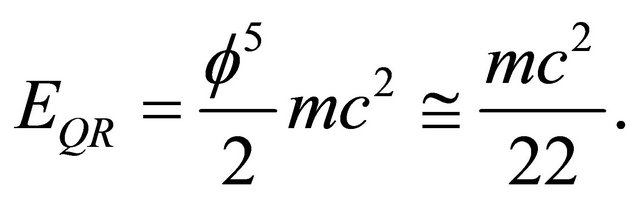 (19)
(19)
Seen that way the reduction of E from the 100% of Einstein’s theory to the 4.5% of the exact quantum relativity theory is due to quantum entanglement at the Hubble cosmic distances (see Figure 4) which could be explained rationally via the zero measure of fractal Cantorian geometry [10-13]. The second method we will use to derive the same previous formula is to go back to relativistic boost and then connect it to the random Cantor sets topology. We start with the three well documented relativistic effects namely time dilation, shortening of spatial extension and mass increase at  That means [5, 22]
That means [5, 22]
 (20)
(20)
where  is a boost which needs not be specified at this point. Setting in Newton’s kinetic energy one finds [5]
is a boost which needs not be specified at this point. Setting in Newton’s kinetic energy one finds [5]

Figure 2. Unit interval physics, ultimate F and Taiji-El Naschie theory.

Figure 3. T-duality and the quantum cosmic domain.
 (21)
(21)
Taking  to be Sigalotti’s critical value
to be Sigalotti’s critical value  [20, 21] one finds the same previous result
[20, 21] one finds the same previous result
 (22)
(22)
7. Discussion and Prospects
For the last thirty years or so nonlinear dynamics became an indispensible tool for countless branches of engineering and applied sciences as well as mathematics [13]. By comparison high energy and quantum physics was slow to utilize the tremendous possibilities offered by deterministic chaos and fractal geometry [2,10,11,13]. The situation changed radically in the last five years or so. In particular the success of resolving fundamental problems such as the mystery of dark energy and quantum entanglement is paving the way towards a reappraisal of many fundamental problems in theoretical physics and cosmology from the point of view of nonlinear dynamics, chaos and fractals [1,2,11,13]. It is an accurate statement to claim that the word Notion and the concept of self-similarity and self-affinity became indispensable tools of exact science only after the rise to prominence of non-linear dynamics, chaos and fractals some three decades ago [1, 2]. This is what made it possible to apply global analysis in conjunction with fractal geometry in relativistic quantum cosmology and discover that Newton’s kinetic energy  as well as Einstein’s relativistic formula
as well as Einstein’s relativistic formula  and the new quantum relativistic energymasse equivalence equation EQR;
and the new quantum relativistic energymasse equivalence equation EQR;  are merely self-similar scaling of each other in the sense of modern nonlinear dynamical theories [22]. We could go even several steps further and realize that a fractal form of Legendre transformation leads us to recognize that the
are merely self-similar scaling of each other in the sense of modern nonlinear dynamical theories [22]. We could go even several steps further and realize that a fractal form of Legendre transformation leads us to recognize that the

Figure 4. The t-duality connecting high energy physics with cosmology.
energy formula for dark energy is given directly by
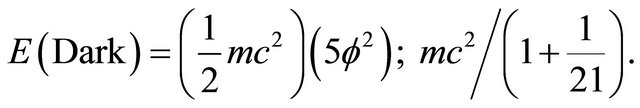 (23)
(23)
This obviously is the complementary energy of the ordinary energy
 (24) Adding both expressions we find that (see Figure 5)
(24) Adding both expressions we find that (see Figure 5)
 (25)
(25)
We draw here attention to the T-duality (see Figure 3) and the unit interval physics behind this incredibly simple and elegant relations reconciling classical physics with relativity and quantum theory. It is remarkable that the same physics behind the very large meets at “infinity” with physics of the extremely small unifying high energy with cosmology (see Figure 4) and all via the magnificent concept and mathematics of renormalization.

Figure 5. Flow chart for the logical connection between Newton kinetic energy and ordinary energy, dark energy and Einstein energy. Note that ordinary energy is the energy of the quantum particle and dark energy is the energy of the quantum wave in 5 dimensions.
In turn this mathematics is nothing more than taming all singularities using fractal self-similarity [1,2].
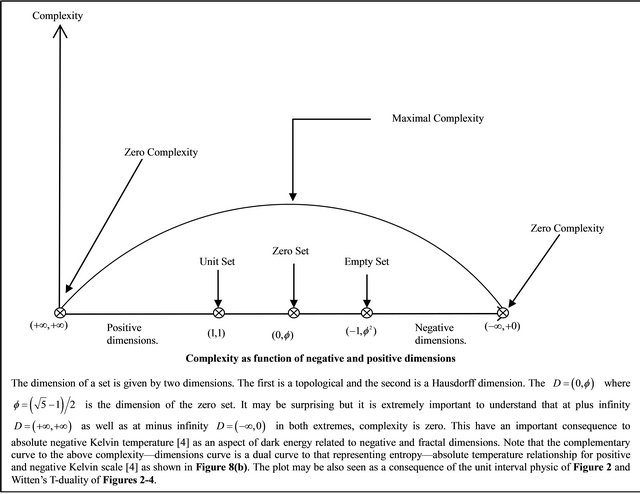
This conclusion has momentous ramifications going as far as showing the existence of negative gravity (see Figure 6) as well as explaining the fractal rationale behind the mystery of the constancy of the speed of light (see Figure 7) and negative absolute temperature [4] (see Figure 8).
8. Conclusion
Nonlinear dynamics, chaos and fractals have enriched science and gave theoreticians meantime various new indispensable mathematical tools such as self-similarity, average symmetry and fuzzy group theories [2,11]. High energy physics was relatively late in utilizing these new methods, but things have flourished in the last five years thanks to the dedicated work of various schools which applied nonlinear dynamics to particle physics and cosmology [1,8,9,12]. We were able to reason that dark energy is related to compactified and fractal extra-dimensions zero and empty sets which employ fractals and Cantorian sets [5,22]. That way we were in a position to derive a fundamental quantum relativity equation
 (26)
(26)
and a second complementary equation (see Figure 5)
 (27)
(27)
The sum of both equations is exactly equal to Einstein’s famous equation which doesn’t distinguish between ordinary energy and dark energy i.e.  It is important to notice that the ratio of E(Dark) to E(Ordinary) is exactly equal to
It is important to notice that the ratio of E(Dark) to E(Ordinary) is exactly equal to
 .
.
In other words this is the 26 + k of transfinite bosonic string theory minus the five dimensions of Kaluza-Klein theory. Seen that way dark energy is related to the compactified section of space-time of bosonic strings which represents negative curvature and thus negative energy and negative gravity (see Figure 6) leading to the observed acceleration of the universe. That way nonlinear dynamics, deterministic chaos theory and Cantorian fractals seem to have succeeded in solving yet another major mystery in current modern cosmology [3,5,6]. It is consequently reasonable to accept that further intensive future research using modern nonlinear dynamics and Ultimate L set theory [18] will give a final resolution to

Figure 6. The driving force behind gravity and negative gravity. Here D(4) = 4 is the dimension of Einstein’s space-time, R(4) = 20 is the number of independent components of Riemann curvature tensor in four dimensions and R(4) = 256 is the number of all the components of the same curvature tensor, v is the velocity and c is the speed of light.

Figure 7. The experimentally observed constancy of the speed of light as a probabilistic expectation value of a Cantorian fractal space-time.
 (a)
(a) (b)
(b)
Figure 8. (a) Complexity as function of negative and positive dimensions; (b) Entropy as function of negative and positive dimensions.
the deep problems of the true meaning of time, gravity and the constancy of the speed of light which we outlined here in Figures 3, 4, 6 and 7. In addition we tackled negative absolute temperature and it’s dual relation to negative dimensions and relevance to negative gravity and dark energy [4,23] (see Figure 8).