Risk-Sensitive Asset Management under a Wishart Autoregressive Factor Model ()
1. Introduction
1.1. Risk-Sensitive Asset Management
Consider a continuous-time financial market that consists of one riskless asset and  risky assets. The price process of the riskless asset
risky assets. The price process of the riskless asset  and that of the
and that of the
 risky assets
risky assets ,
,  , where
, where
 denotes the transpose of a vector or matrix, are semimartingales defined on a filtered probability space
denotes the transpose of a vector or matrix, are semimartingales defined on a filtered probability space . Define the wealth process
. Define the wealth process  of a self-financing investor governed by the following stochastic differential equation (SDE):
of a self-financing investor governed by the following stochastic differential equation (SDE):
 (1.1)
(1.1)
where  is the initial wealth of the investor, and
is the initial wealth of the investor, and ,
,  is the dynamic investment strategy of the investor. Let
is the dynamic investment strategy of the investor. Let
 (1.2)
(1.2)
be the growth rate of the wealth at time . For given constants
. For given constants  and
and , define the risksensitized expected value of
, define the risksensitized expected value of  by
by

which is rewritten as

and interpreted as the certainty equivalent value of  with respect to the exponential criterion function
with respect to the exponential criterion function . We are interested in maximizing
. We are interested in maximizing , that is,
, that is,
 (1.3)
(1.3)
which we call the risk-sensitive asset management problem. Here,  is a space of admissible investment strategies and is a subset of
is a space of admissible investment strategies and is a subset of , the totality of
, the totality of 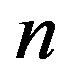 -dimensional
-dimensional  -progressively measurable processes
-progressively measurable processes
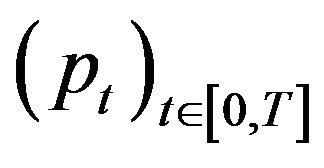 on the time interval
on the time interval  such that
such that  almost surely.
almost surely.
Remark 1.1 The risk-sensitive asset management problem (1.3) has been well-studied under a linear-Gaussian market model, for example, by [1-7]. In those works, the price processes  are given by the solutions to the following system of SDEs:
are given by the solutions to the following system of SDEs:
 (1.4)
(1.4)
on a filtered probability space  endowed with the
endowed with the  -dimensional
-dimensional  -Brownian motion
-Brownian motion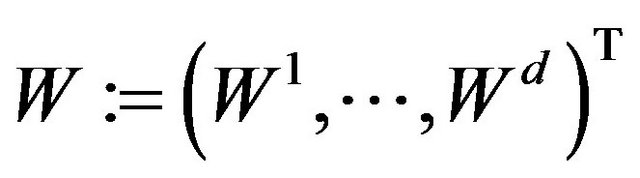 ,
, . Here,
. Here,  denotes the diagonal matrix whose
denotes the diagonal matrix whose  th element is equal to the
th element is equal to the  th element
th element  of
of ,
,  ,
,  , and
, and
 (1.5)
(1.5)
with ,
,  ,
,  ,
,  ,
,  ,
,  , and
, and . We reformulate (1.3) with (1.1), (1.2), (1.4), and (1.5) as a linear exponential quadratic Gaussian stochastic control problem, and the optimal investment strategy (portfolio)
. We reformulate (1.3) with (1.1), (1.2), (1.4), and (1.5) as a linear exponential quadratic Gaussian stochastic control problem, and the optimal investment strategy (portfolio)
 for (1.3) is represented explicitly:
for (1.3) is represented explicitly:

Here,  is the solution to a matrix differential Riccati equation, and
is the solution to a matrix differential Riccati equation, and  is the solution to a linear differential equation, including
is the solution to a linear differential equation, including .
.
Remark 1.2 Intuitively, recalling the cumulant expansion,

where  denotes variance, we interpret (1.3) as a risk-sensitized optimization of the expected growth rate maximization,
denotes variance, we interpret (1.3) as a risk-sensitized optimization of the expected growth rate maximization,

1.2. Wishart Factor Model
The main aim of the present paper is to introduce a simple and tractable market model that satisfies the following requirements:
• The model describes the stochasticity of the covariance structure of , interest rates, and mean-return rates of
, interest rates, and mean-return rates of .
.
• The model admits an explicit representation of the optimal investment strategy for (1.3).
For the purpose, we employ a Wishart autoregressive process as a stochastic factor, which is positive-definite symmetric matrix-valued. Such matrix-valued processes have been introduced and studied by [8], and recently, generalizations have been intensively studied, for example, see [9,10], and the references therein. Moreover, these processes are now extensively utilized for financial modeling. We can refer to the examples given below.
• Modeling of multivariate stochastic volatility (covariance) under the risk-neutral probability: see [11-16].
• Modeling of multivariate asset price process under physical probability with stochastic covariance and mean-return rates: see [14,17,18].
• Modeling of (term structure of) interest rates and stochastic intensity for credit risk: see [14,17,19,20].
Our market model defined by (2.1)-(2.4) in Section 2 is an extension of the model employed by [18], (see Example 2.1), who studied the expected CRRA-utility ma ximization of terminal wealth, which is essentially equivalent to (1.3). A main contribution of the present paper is a rigorous mathematical analysis of portfolio optimization problem (1.3) under a flexible Wishart autoregressive stochastic factor model: We strengthen the mathematical results in [18] by formulating an appropriate space of admissible trading strategies (see (3.5)) and showing a verification theorem for the candidate of the optimal strategy (see Theorem 3.1), both of which are omitted in [18].
In the next section, we introduce our market model with a Wishart autoregressive factor and present preliminary calculations of the associated Hamilton-JacobiBellman (HJB) equation for solving risk-sensitive asset management problem (1.3). In Section 3, we introduce our main results. In Section 4, we show the proof of the main theorem after preparing lemmas.
2. Setup
2.1. Market Model with Wishart Autoregressive Factor
Let  be a filtered probability space endowed with the
be a filtered probability space endowed with the  -dimensional
-dimensional  -Brownian motion
-Brownian motion ,
,  , and the
, and the
 -dimensional
-dimensional  -Brownian motion
-Brownian motion ,
,
 , which is independent of
, which is independent of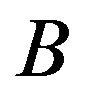 . Using a constant vector
. Using a constant vector  so that
so that , we define another
, we define another  -dimensional Brownian motion
-dimensional Brownian motion
 ,
,  by
by

which is correlated with  as
as

where  denotes the quadratic covariation, and
denotes the quadratic covariation, and  denotes Kronecker’s delta. We consider the price processes
denotes Kronecker’s delta. We consider the price processes , described by the following system of SDEs:
, described by the following system of SDEs:
 (2.1)
(2.1)
with the initial values ,
,  and
and . Here, we denote by
. Here, we denote by  the totality of
the totality of  -dimensional, real, symmetric matrices, and
-dimensional, real, symmetric matrices, and . Furthermore, for
. Furthermore, for , we define
, we define
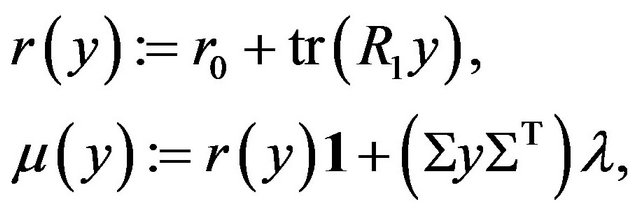 (2.2)
(2.2)
where ,
,  , and
, and . Also, we assume that
. Also, we assume that  is full rank, that is,
is full rank, that is,
 (2.3)
(2.3)
We also assume that , and that
, and that  satisfies
satisfies
 (2.4)
(2.4)
Condition (2.4) ensures  almost everywhere on
almost everywhere on , which was established by Mayerhofer et al. (2011) using a generalized form of SDE, including a jump martingale part. The
, which was established by Mayerhofer et al. (2011) using a generalized form of SDE, including a jump martingale part. The  -valued process
-valued process  is a stochastic factor process, which linearly depends on the covariance structure of
is a stochastic factor process, which linearly depends on the covariance structure of  as
as
 (2.5)
(2.5)
as well as on the interest rate
 (2.6)
(2.6)
and on the so-called risk premium of ,
,
 (2.7)
(2.7)
Remark 2.1 From (2.6), we see that the interest rate process  is included in the so-called affine class:
is included in the so-called affine class: 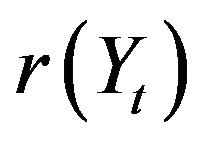 is an affine function of
is an affine function of  and the process
and the process , whose infinitesimal generator is given by
, whose infinitesimal generator is given by
 (2.8)
(2.8)
where  and
and
 (2.9)
(2.9)
is indeed an affine diffusion. To review affine processes and their financial applications, see, for example, [21], [22], and the references therein.
Remark 2.2 The condition (2.7) on the structure of the risk-premium vector is rewritten as

So we interpret that the so-called mean-variance term in portfolio optimization theory is assumed to be constant.
The following are concrete examples of setting up (2.1) and (2.2).
Example 2.1 (Stochastic Covariance) Let

Concretely, we have

with the third equation in (2.1).  describes the infinitesimal covariance and the risk premium of
describes the infinitesimal covariance and the risk premium of  as
as

and

This is exactly the model employed in Section 1 of [18] to study expected CRRA-utility maximization of terminal wealth.
Example 2.2 (Stochastic Covariance and Interest Rate) We present a slight generalization of Example 2.1 to include stochasticity of interest rates. Let
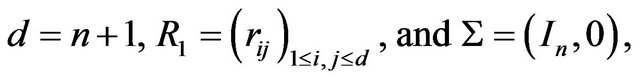
where we set  if
if . Then, letting
. Then, letting

and , we see that
, we see that

is the risk-free interest rate with the latent factor  and that
and that

where  describes the infinitesimal covariance and the risk premium of
describes the infinitesimal covariance and the risk premium of  as
as

and

Example 2.3 (Cox-Ingersoll-Ross Interest Rate Factor) Let

Then, we see
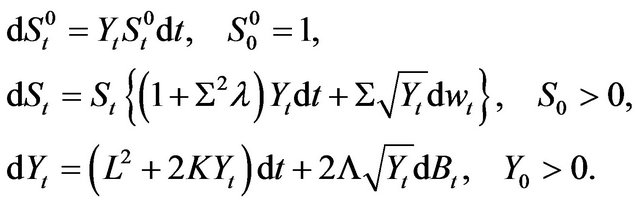
This financial market model with Cox-Ingersoll-Ross’s interest rate  is treated in [23] to study (1.3).
is treated in [23] to study (1.3).
Under the financial market model comprising (2.1) and (2.2) with the assumptions (2.3) and (2.4), we are interested in treating the risk-sensitive asset management problem (1.3).
2.2. Deriving the HJB Equation
To tackle (1.3), we employ a dynamic programming approach: Recall that wealth process (1.1) of a selffinancing investor, combined with (2.1), is rewritten as

So, we see

where we set
 (2.10)
(2.10)
Hence, we have

where we define
 (2.11)
(2.11)
Let

For , we define the probability measure
, we define the probability measure  on
on  by the formula
by the formula

By Cameron-Martin-Maruyama-Girsanov’s theorem, we see that the  -valued process
-valued process , defined by
, defined by

is a  -Brownian motion. Moreover, we see that
-Brownian motion. Moreover, we see that  has the
has the  -dynamics
-dynamics

Recall that, for , we have
, we have
 (2.12)
(2.12)
where  denotes the expectation with respect to
denotes the expectation with respect to . We now consider, for
. We now consider, for ,
,

where

The associated HJB equation is written as
 (2.13)
(2.13)
By direct calculation, we can see the following.
Lemma 2.1 1) If  and
and , then HJB Equation (2.13) is rewritten as
, then HJB Equation (2.13) is rewritten as
 (2.14)
(2.14)
where we define
 (2.15)
(2.15)
The maximizer for (2.13) is given by

2) If  and
and , then HJB equation (2.13) is rewritten as
, then HJB equation (2.13) is rewritten as
 (2.16)
(2.16)
where  and
and  are given by (2.15). The maximizer for (2.13) is given by
are given by (2.15). The maximizer for (2.13) is given by

3. Results
With the help of Lemma 2.1, it is straightforward to see the following.
Proposition 3.1 (Solution to the HJB equation) 1) If , then
, then
 (3.1)
(3.1)
solves (2.13), or equivalently (2.14). Here,  and
and  solve the following system of ordinary differential equations:
solve the following system of ordinary differential equations:
 (3.2)
(3.2)
2) If , then
, then
 (3.3)
(3.3)
solves (2.13), or equivalently (2.16). Here,  and
and  solve the following system of ordinary differential equations:
solve the following system of ordinary differential equations:
 (3.4)
(3.4)
Using this proposition, we obtain the following.
Theorem 3.1 (Verification and optimal strategy)
Define the filtration  by
by
 . Let
. Let
 (3.5)
(3.5)
and consider (1.3) with . Then, the following assertions hold.
. Then, the following assertions hold.
1) If , then
, then , defined by
, defined by
 (3.6)
(3.6)
is optimal for (1.3). It holds that
 (3.7)
(3.7)
2) If , then
, then , defined by
, defined by
 (3.8)
(3.8)
is optimal for (1.3). The relation (3.7) holds.
The proof of the above theorem is given in Subsection 4.2 after preparing lemmas in Subsection 4.1.
4. Proofs
4.1. Lemmas for Exponential Martingale
We prepare the following two lemmas.
Lemma 4.1 Let  be
be  -progressively measurable so that
-progressively measurable so that
 almost surely for all
almost surely for all .
.
Define


Then,  is an
is an 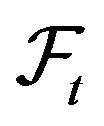 -martingale if and only if
-martingale if and only if  is an
is an  -martingale.
-martingale.
Proof. Denote . For
. For  , we have
, we have

Lemma 4.2 Let  satisfy the following: for each
satisfy the following: for each ,
,  is
is  -measurable, and
-measurable, and

with some bounded , where we write
, where we write 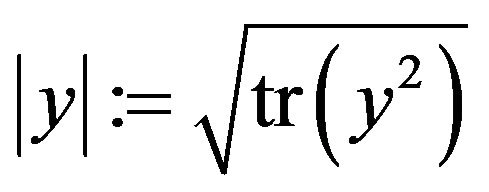 for
for . Then, the process
. Then, the process , defined by
, defined by

is a martingale.
Proof. The lemma follows from Lemma 4.1.5 of [24], an extension of Lemma 4.1.1 of [25]. Below, we reproduce the proof for self-containedness. Note that it suffices to show
 (4.1)
(4.1)
Recall that  is progressively measurable. The proof of (4.1) consists of several steps.
is progressively measurable. The proof of (4.1) consists of several steps.
First, writing , we recall that
, we recall that
 (4.2)
(4.2)
where  is defined by (2.8). From this, we can check that
is defined by (2.8). From this, we can check that

for each  with some constant
with some constant . Also, we can check that
. Also, we can check that
 (4.3)
(4.3)
This follows from the relation
 (4.4)
(4.4)
where  is arbitrary and the constant
is arbitrary and the constant  is independent of
is independent of . Indeed, in (4.4), letting
. Indeed, in (4.4), letting  and using Fatou’s lemma, (4.3) is deduced. To see (4.4), use (2.1) and Itô’s formula to deduce
and using Fatou’s lemma, (4.3) is deduced. To see (4.4), use (2.1) and Itô’s formula to deduce


where we use notation (2.8) and (2.9). From these, we see, from Itô’s formula,

where

is the local-martingale part and  is the bounded-variation part, which satisfies
is the bounded-variation part, which satisfies

with some constant , independent of
, independent of . We can check that
. We can check that ; hence,
; hence,  is a square-integrable martingale. Further, using (4.2) and recalling that
is a square-integrable martingale. Further, using (4.2) and recalling that  for conformable matrices
for conformable matrices  and
and , we can check that
, we can check that

with some positive constant , independent of
, independent of . So, taking the expectation, we deduce that
. So, taking the expectation, we deduce that

and that (4.4) follows from Gronwall’s inequality.
Next, use Itô’s formula for the following computation:
 (4.5)
(4.5)
Here, we see that

with some constant ; hence, the first term of the righthand side of (4.5) is a square-intergrable martingale. Also, we can deduce that
; hence, the first term of the righthand side of (4.5) is a square-intergrable martingale. Also, we can deduce that

where  is a positive constant, independent of
is a positive constant, independent of . Taking the expectation, we see
. Taking the expectation, we see

Letting  and using the dominated convergence theorem, we obtain (4.1).
and using the dominated convergence theorem, we obtain (4.1).
4.2. Proof of Theorem 3.1
Let  be given by (3.1). Fix
be given by (3.1). Fix  and take
and take . Using these, define
. Using these, define
 (4.6)
(4.6)
where we use (2.10), (2.11), and the process  given by (2.1), and we set
given by (2.1), and we set . Using Itô’s formula, we see that
. Using Itô’s formula, we see that
 (4.7)
(4.7)
where we define the process  by
by
(see below)
Combining (4.6)-(4.8), we have, for ,
,

Here, note that  is a martingale for any
is a martingale for any  by using Lemma 4.1 and 4.2 and that
by using Lemma 4.1 and 4.2 and that  almost everywhere on
almost everywhere on
 since
since  solves HJB-equation
solves HJB-equation
(2.13). So we deduce that  is a submartingale for each
is a submartingale for each . Taking the expectation, we see that
. Taking the expectation, we see that

Thus, we see that
 (4.9)
(4.9)
for any . Furthermore, if we define
. Furthermore, if we define  by
by

then, we deduce that  almost everywhere on
almost everywhere on , from which we see that
, from which we see that
 is a martingale. Therefore, taking the expectation, we see that
is a martingale. Therefore, taking the expectation, we see that

that is,
 (4.10)
(4.10)
Combining (4.9) and (4.10), we deduce that
 (4.11)
(4.11)
Thus, letting  in (4.11), we have that
in (4.11), we have that

(4.8)and write


(3.7) follows from relation (2.12).