1. Introduction
This decade is seeing tremendous change in the electronics market with the development and commercialization of new technologies in mobile communication, personal computers and the Internet. Niobium and tantalum compounds are being used successfully in a variety of different applications in the electronic and electro-optic markets. The need for miniaturization and high-performance electronic components is leading to more research in nanostructured materials. Characterizing the fundamental properties of these nanoscale constructions is of prime importance. The surface structural properties are of immense importance when artificial fabrication of materials with desirable properties is sought. Owing to the large advancements in thin film depositing techniques and the technological importance of the transition metals, study of the surface energetics of the transition metals is a rapidly growing field. It is essential to have detailed information on the relaxed geometry and energetics of the system to understand completely the factors influencing the epitaxy of interfaces and multilayers. Reliable information on the clean (bare) surface properties is necessary before multi-layer or interface studies can be performed. The growing use of Nb and Ta in nanotechnology requires a clear understanding of the surface properties of these metals. In this paper the surface energies and work functions of the Nb, and Ta (001) relaxed surfaces at zero Kelvin are reported using the total energy pseudopotential method under DFT. Norm conserving pseudopotentials with a plane wave basis set is used to vastly reduce computer time and still maintain the desired accuracy. DFT has the double advantage of being able to treat many problems to sufficiently high accuracy, as well as being computationally simple [1-4]. Over the last forty years or so DFT has gained tremendous popularity and it is currently one of the most widely used methods for “ab initio” calculations of the structure of atoms, molecules, crystals, surfaces, and their interactions.
The purpose of the present work is to take into account a complete relaxation of the atomic positions for the calculation of the surface properties. Since, most of the existing first principles calculations [5-7] have assumed truncated bulk geometry of the surface this is highly desirable. In addition this is the first study of these systems with the DFT-total energy pseudopotential method. The agreement of the results with those obtained by other methods proves the reliability of this method and is also one of the motivations.
2. Calculation Details
The Niobium and Tantalum (001) surfaces are modeled by periodic slabs consisting of 7 to 13 layers, separated by several layers of vacuum, equivalent to almost 70% - 75% of the slab thickness. On account of the large and persistent relaxations at the relatively open (001) surfaces, especially transition metals performing the calculations for slabs of 7 - 13 atomic layers helps to check the convergence of the results. Even though, for all practical purposes the 9 or 11-layer slab is thick enough to avoid perturbation connected with the finite/periodic geometry and can represent well all the surfaces considered.
All calculations are performed using the ABINIT software package with norm conserving pseudopotentials [8]. In all cases the Hartwigsen, Goedecker, and Hutter (HGH) pseudopotentials [9] are used for LDA calculations and the Perdew, Burke and Ernzerhof (PBE) form of the GGA pseudopotentials are used for GGA calculations [10]. The in-plane lattice constant used for the slab is that obtained from bulk calculations for Nb and Ta. The cutoff energy and the number of k-points defining the plane wave basis set for each of the surfaces is obtained after careful convergence tests of these quantities with respect to the total energy. The surface geometry is optimized using Broyden-Fletcher-Goldfarb-Shanno (BFGS) minimization algorithm with a total maximum force of less than 1 mRy/a.u. as convergence criteria [11].
3. Results and Discussion
The lattice constants used in this study of the Nb and Ta (001) surfaces are calculated from first principles, self consistently, both for the GGA and LDA calculations. The optimized lattice constant values, the cutoff energy and the k-point grid are listed in Table 1. The table also shows the percentage difference between the calculated and experimental values [12]. It can be seen that the GGA values are slightly bigger than the LDA ones, but all are within ±1% - 2% of the experimental values. The results of this work are subdivided under four sub-headings.
3.1. Surface Lattice Relaxation
The structural relaxation of the clean Nb and Ta (001) surfaces is performed for the various atomic layer slabs and the percentage relaxations of the atomic layers are calculated using the relation:
 (1)
(1)
where  is the distance between two successive layers in the relaxed surface structure and ∆Bulk is the interlayer bulk distance. The GGA relaxation results are summarized in Table 2. The values for the 9 layers are very close to those obtained for 11 layers, within ±0.02. It can be seen from the table that the top-layer relaxation changes only a small amount when the number of layers in a slab is increased. For deeper layers, the relaxations vary in an oscillatory way. Minus and plus signs denote contraction and expansion, respectively. The vertical relaxations of deeper layers are damped rather quickly and converge to the bulk interlayer spacing. Note the relaxations do not vanish completely for the deeper, central layers of the slab but it is negligibly small and within 0.5% - 1% of the bulk value. The relaxation results are also shown in the graphical form in Figure 1 where the behavior of the Nb and Ta surfaces upon relaxation can be clearly observed. The
is the distance between two successive layers in the relaxed surface structure and ∆Bulk is the interlayer bulk distance. The GGA relaxation results are summarized in Table 2. The values for the 9 layers are very close to those obtained for 11 layers, within ±0.02. It can be seen from the table that the top-layer relaxation changes only a small amount when the number of layers in a slab is increased. For deeper layers, the relaxations vary in an oscillatory way. Minus and plus signs denote contraction and expansion, respectively. The vertical relaxations of deeper layers are damped rather quickly and converge to the bulk interlayer spacing. Note the relaxations do not vanish completely for the deeper, central layers of the slab but it is negligibly small and within 0.5% - 1% of the bulk value. The relaxation results are also shown in the graphical form in Figure 1 where the behavior of the Nb and Ta surfaces upon relaxation can be clearly observed. The
Table 1. The lattice constants and basis sets in LDA and GGA.

aPercentage difference in lattice constants—present calculations and experimental results [12].
Table 2. The percentage interlayer relaxation of the different layers of the Nb, and Ta (001) clean surfaces in GGA, the LDA values are given in the last row for each surface.
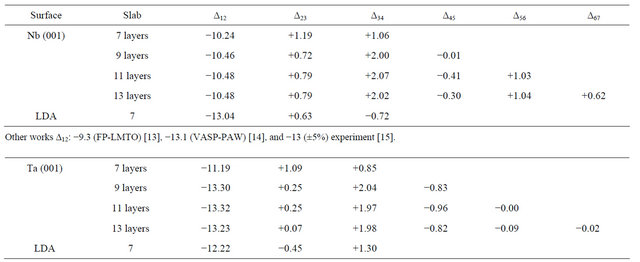
Other works ∆12: −13.9 (DFT-GGA) [16], −11.0 (LEED) [17], and −10.0 (±5) other experiment [18].
 (a)
(a)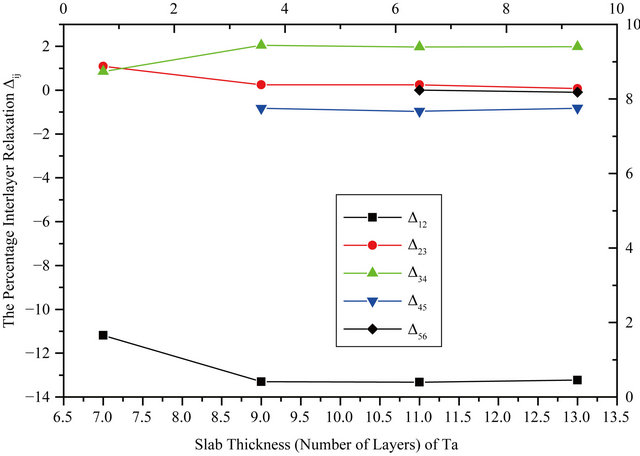 (b)
(b)
Figure 1. Surface relaxation as a function of slab thickness.
results of other theoretical and experimental works including that of LEED for the topmost layer relaxation are presented at the end of each surface data [13-18]. The relaxation behavior of the different surfaces is in close agreement to other works. It can be noticed that the topmost layer relaxation converges excellently with the number of layers for Nb and for Ta within an uncertainty of ±0.1. Table 2 also shows the LDA results in the last row for each surface below the GGA ones. The LDA results are all in good agreement with the GGA values within 2%.
3.2. Surface Energies
The formation energy of a solid surface can be extracted from thin slab calculations if the bulk energy per atom is known. The surface energy is calculated using the relation:
 (2)
(2)
where En is the energy per unit cell of the n layer slab and EB is the bulk energy of the infinite solid per unit cell. The factor of half arises from the 2 surfaces of the slab. A direct application of the formula (2) usually leads to a linear divergence with the increasing slab thickness if EB is determined from an independent bulk calculation [19]. Thus, in this calculation, the bulk energy is determined as the total energy increment of the slab, upon addition of one layer of the metal, i.e. using the slab-related quantities only. The EB is taken as an average of the energy increment values for the unrelaxed slabs of n layers and n ± 1 layers. For example to calculate the surface energy of the 7 layer slab, the average of the total energy difference of the 6 layer and 8 layer slabs from the 7 layer slab is taken as the bulk energy. Table 3 presents the relaxed surface energies for the different surfaces in GGA. From it one can see that the surface energies converge very well with respect to the number of layers for both the Nb and Ta surfaces. A graphical visualization of this fact is through Figure 2 which shows the relaxed surface energies as a function of the number of layers. The difference between the relaxed and non-relaxed surface energies is within 0.5 eV for all layers and surfaces under consideration.
The results of other calculations have been included alongside for comparison. There is good agreement with the work of Vitos et al. for the Niobium surface [5]. For the Tantalum surface the results are closer to the work of Keinja [16] for the 11 layers. The higher values obtained by Vitos et al. for this surface could be due to their neglect of relaxation [5]. The results are also in good agreement with other theoretical works. In addition, the results obtained agree very well with the experimental results available for the Nb (001) surface and are in good agreement with both the experimental works [20,21]. There is no available experimental determination of the surface energy of the Ta (001) surface and this is highly desirable. Regarding the LDA calculations, only calculations for the 7 layers slab were performed for both the surfaces. This is sufficient to show the effect of exchange correlation and also to make comparison with the other available theoretical calculations. The LDA results have been included in the last row of the results for each surface in Table 3. There is good agreement with the corresponding GGA values and other works for 7 layers slabs.
3.3. Work Functions
The work function corresponds to the minimum amount of energy needed to remove an electron from the metal and for a metallic slab may be expressed as the difference between the electrostatic potential barrier height in the vacuum, Ves, and the Fermi energy, EF
 (3)
(3)
In metals, the work function and ionization energy are the same. The work function of a surface is strongly affected by the condition of the surface. The presence of minute amounts of contamination (less than a monolayer of atoms or molecules), or the occurrence of surface reactions (oxidation or similar) can change the work function substantially. Theoretical first principles determinations of work function are therefore very useful. The calculated work functions for the relaxed surfaces in GGA are listed in Table 4. The LDA results for the 7 layer slabs are also included at the end for both the Nb and Ta (001) surfaces.
Table 4 shows that the results of GGA and LDA calculations are in close agreement within 0.3 eV. Moreover, the GGA work function values converge excellently within 0.03 eV with the increasing number of layers. This convergence is clearly seen in Figure 3 which shows the work function variation with the number of layers for Nb and Ta relaxed surfaces. For all practical purposes the 7 layer slab and the 9 layer slab can well represent the Nb
Table 3. The GGA relaxed surface energies of the different layers of the Nb, and Ta (001) clean surfaces. Results of other theoretical calculations are shown alongside with the corresponding reference in square brackets. The experimental results are also shown whenever available. The LDA values are given in the last row for each surface.
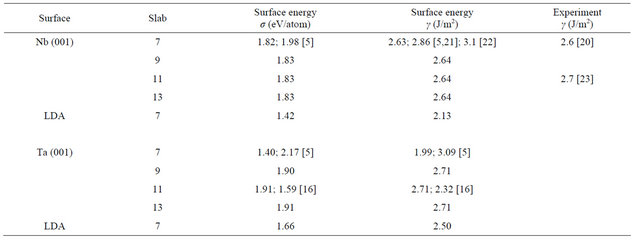
Table 4. The GGA relaxed work functions for the different layers of the Nb, and Ta(001) clean surfaces. The LDA values are given in the last row for each surface. Results of other theoretical calculations are also shown with the corresponding reference in square brackets. The experimental results are also shown whenever available.
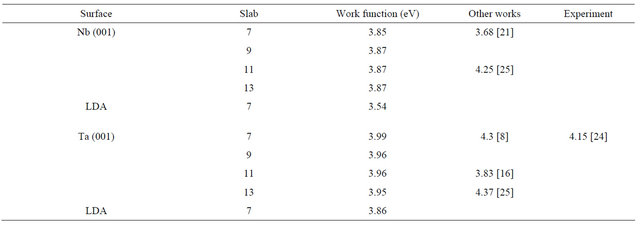
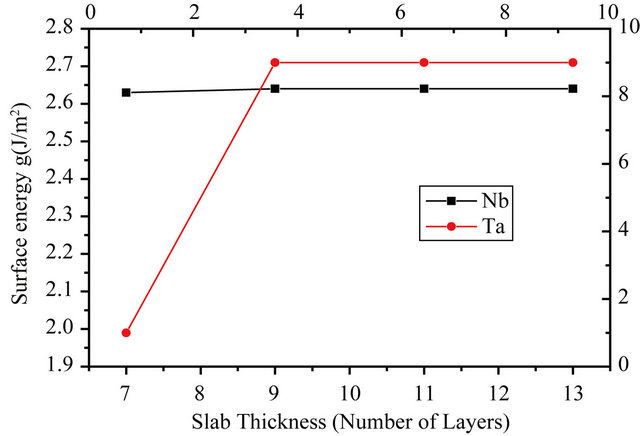
Figure 2. The relaxed surface energy as a function of slab thickness.

Figure 3. The relaxed work function as a function of slab thickness.
and Ta surfaces. There is also good agreement with other ab-initio calculations and experiment. The small discrepancies can be attributed to the neglect of relaxations in the other works or may arise from the different exchangecorrelation energy functional applied. As far as experimental value is concerned, the only available one is for the Ta surface and that too is old. Experimental verification of the results for all the surfaces would be highly desirable.
3.4. Conclusions
1) Surface relaxations, surface energies, and work functions of the (001) surfaces of Niobium and Tantalum are determined at zero Kelvin from first principles using DFT with the GGA and LDA exchange-correlation functional. Results obtained with both the exchange correlations are in good agreement for all the surfaces considered. Surface energies and work functions all agree within 0.5 eV.
2) There is very good convergence with respect to the number of layers in the slab for all the properties in all the surfaces.
3) There is good overall agreement with the results of other ab-initio calculations and experimental results. This is a big boost for DFT methods of calculation which is increasingly becoming more and more popular and gaining wide spread acceptance.