Commuting Structure Jacobi Operator for Real Hypersurfaces in Complex Space Forms ()
1. Introduction
Combined heat and mass transfer driven by buoyancy due to temperature and concentration is of practical importance, since there are many possible engineering applications, such as the migration of moisture through the air contained in fibrous insulations and grain storage installation, and dispersion of chemical contaminants through water-saturated solid. The state of art concerning combined heat and mass transfer in porous media has been summarized in the excellent monographs by Nield and Bejan [1]. In addition, coupled heat and mass transfer can interpret certain natural phenomena such as ocean currents driven by differential heating and act as freight trains for salt as mentioned by Bejan [2], and the role of factory waste gas diffusion in a differential heating circulated air. There has been considerable work done on the study of flow and heat transfer in geometries with and without porous media (for instance, Vafai and Tien [3] and Churchill and Chu [4]).
A study on “unsteady free convection on a vertical cylinder with variable heat and mass flux” has wide range of applications. The importance of this study lies in the fact that this type of boundary condition is commonly met with in practice. A study of temperature and mass distribution around the intrusive and the associated variable heat and mass surface change is important in the geothermal resources during geophysical exploration. The intrusive may be taken as vertical cylinder with power law heat flux and mass flux boundary condition. Some transient results are given by Evans et al. [5] and Velusamy and Garg [6]. But their study confined to heat transfer from a vertical cylinder.
Chemical reactions can be codified as either heterogeneous or homogeneous processes. This depends on whether they occur at an interface or as a single phase volume reaction. A few representative fields of interest in which combined heat and mass transfer plays an important role, are design of chemical processing equipment, formation and dispersion of fog, distribution of temperature and moisture over agricultural fields and groves of fruit trees, damage of crops due to freezing, food processing and cooling towers. Cooling towers are the cheapest way to cool large quantities of water.
The effects of mass transfer on flow past an impulsively started infinite vertical plate with constant heat flux and chemical reaction were studied [7]. The velocity and concentration increased with decrease of the chemical reaction parameter and vice versa Skin-friction and heat transfer analysis of MHD flow for a small Prandtl number fluid past a semi infinite plate were studied [8,9]. Finally, Ghaly and Seddeek [10] studied Chebyshev finite difference method for the effects of chemical reaction, heat and mass transfer on laminar flow along a semi-infinite horizontal plate with temperature dependent viscosity. Recently, Seddeek et al. [11] studied, the effects of chemical reaction and variable viscosity on hydromagnetic mixed convection heat and mass transfer for Hiemenz flow through porous media with radiation.
Hence, the aim of the present work is to study the effects of chemical reaction on unsteady natural convection boundary layer flow over a semi-infinite vertical cylinder. In the present analysis, consideration is given to situations in which the surface of the cylinder is maintained at power law variations of heat and mass flux. The unsteady, non-linear and coupled governing equations are first transformed into a non-dimensional form and their solutions are obtained by an efficient Crank-Nicolson implicit finite-difference method.
2. Mathematical Analysis
A vertical cylinder of radius  which is surrounded by a quiescent bulk fluid with wall temperature subjected to power-law surface heat flux
which is surrounded by a quiescent bulk fluid with wall temperature subjected to power-law surface heat flux  and wall concentration subjected to the power-law surface mass flux
and wall concentration subjected to the power-law surface mass flux  is considered. The axis and radial co-ordinates are taken to be x and r, with the x-axis measured vertically upward along the axis of the cylinder and r-axis measured normal to axis of cylinder. The analysis is confined to species diffusion process in which the diffusion-thermo and thermo-diffusion effects are neglected. By employing the boundary layer approximations, the conservation equations for a Boussinesq fluid can be written as
is considered. The axis and radial co-ordinates are taken to be x and r, with the x-axis measured vertically upward along the axis of the cylinder and r-axis measured normal to axis of cylinder. The analysis is confined to species diffusion process in which the diffusion-thermo and thermo-diffusion effects are neglected. By employing the boundary layer approximations, the conservation equations for a Boussinesq fluid can be written as
 (1)
(1)
 (2)
(2)
 (3)
(3)
 (4)
(4)
The initial and boundary conditions are
 (5)
(5)
Introducing the following non-dimensional quantities
 (6)
(6)
in Equations (1)-(4), they reduce to the following nondimensional form
 (7)
(7)
 (8)
(8)
 (9)
(9)
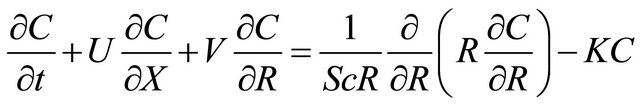 (10)
(10)
The corresponding initial and boundary conditions in non-dimensional quantities are given by
 (11)
(11)
3. Numerical Technique
In order to solve the unsteady, non-linear coupled Equations (7)-(10) under the conditions (11), an implicit finite difference scheme of Crank-Nicolson type is employed. The region of integration is considered as a rectangle with sides  and
and , where
, where  corresponds to
corresponds to  which lies very well outside the momentum, thermal and concentration boundary layers. Appropriate mesh sizes
which lies very well outside the momentum, thermal and concentration boundary layers. Appropriate mesh sizes ,
,  and time step
and time step  are considered for calculations. The finitedifference equations corresponding to Equations (7) to (10) are as follows [12]:
are considered for calculations. The finitedifference equations corresponding to Equations (7) to (10) are as follows [12]:
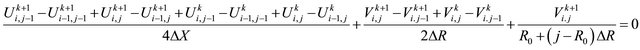 (12)
(12)
 (13)
(13)
 (14)
(14)
 (15)
(15)
The derivative boundary conditions on the surface of the cylinder are written in the following form as
 (16)
(16)
 (17)
(17)
At 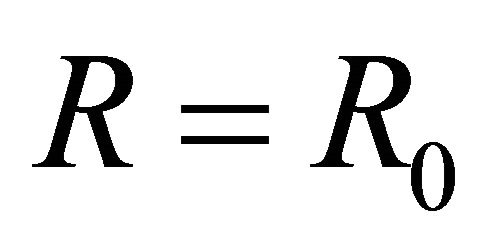 (i.e., at j = 1) Equations (14) and (15) becomes
(i.e., at j = 1) Equations (14) and (15) becomes
 (18)
(18)
 (19)
(19)
After eliminating  from the Equations (16) and (18), and
from the Equations (16) and (18), and  from the Equations (17) and (19) the following equations are obtained.
from the Equations (17) and (19) the following equations are obtained.
 (20)
(20)
 (21)
(21)
Here i-designates X-direction , j-designates Rdirection
, j-designates Rdirection  and the superscript k designates a value of time
and the superscript k designates a value of time . During any one time step, the coefficients
. During any one time step, the coefficients  and
and  appearing in Equations (12)
appearing in Equations (12)
to (15) are treated as constants. The values of U, V, T and C are known at time t = 0 from the initial conditions. The values of C, T, V and U at the next time step  are calculated see [12]. Computations are repeated until the steady-state is reached. The steady-state solution is assumed to have been reached when the absolute difference between values of velocity U, temperature T as well as concentration C at two consecutive time steps are less than 10−5 at all grid points by using maple personal computer software.
are calculated see [12]. Computations are repeated until the steady-state is reached. The steady-state solution is assumed to have been reached when the absolute difference between values of velocity U, temperature T as well as concentration C at two consecutive time steps are less than 10−5 at all grid points by using maple personal computer software.
After experimenting with a few set of mesh sizes, the mesh sizes are fixed at the level ,
,  and
and . In this case, the spatial mesh sizes are reduced by 50% in one direction and then in both directions and the results are compared. It is observed that, when the mesh size is reduced by 50% in the R-direction, the results differ in the fourth decimal place. When the mesh sizes are reduced by 50% in X-direction or in both directions the results are correct to three decimal places. Hence these mesh sizes are considered to be appropriate mesh sizes for calculations. The truncation error in the finite-difference approximation is
. In this case, the spatial mesh sizes are reduced by 50% in one direction and then in both directions and the results are compared. It is observed that, when the mesh size is reduced by 50% in the R-direction, the results differ in the fourth decimal place. When the mesh sizes are reduced by 50% in X-direction or in both directions the results are correct to three decimal places. Hence these mesh sizes are considered to be appropriate mesh sizes for calculations. The truncation error in the finite-difference approximation is  and it tends to zero as
and it tends to zero as ,
,  and
and . Hence the scheme is compatible. The finite-difference scheme is unconditionally stable [12]. Stability and compatibility ensures convergence.
. Hence the scheme is compatible. The finite-difference scheme is unconditionally stable [12]. Stability and compatibility ensures convergence.
4. Results and Discussion
The numerical computations have been carried out for various values of chemical reaction parameter K at Pr = 0.7 (air), 7.0 (water) and for Sc = 0.7 with N =1.0 and n = m = 0.5 using numerical scheme discussed in the previous section. In order to illustrate the results graphically, the numerical values are plotted in Figures 1-12. These figures depict the transient velocity profiles (U), transient concentration profiles (C) and transient temperature profiles (T) for both Pr = 0.7 (air) and Pr = 7.0 (water) cases. The local Nusselt number, the local Sherwood number and the local skin-friction are illustrated graphically to elucidate interesting features of the solutions.
Figures 1-3 illustrate, the average skin-friction, Nusselt number and Sherwood number respectively as a function of time t covering various parametric values of Pr, Sc, N, n and m. Average skin-friction, Nusselt number and Sherwood number increases with t and after certain lapse of time they are steady throughout the transient period. Average skin-friction gets reduced with increasing values of Sc or m, but it gets increased with N throughout the transient period.
The transient velocity, the transient concentration and the transient temperature are shown in Figures 4-6 respectively. Time taken to reach steady-state depends upon both the Prandtl and Schmidt number. The time required to reach the steady-state increases as Pr and Sc increases. But the steady-state velocity decreases as Pr increases or Sc increases.
Figures 7-9 lower temperature profiles are observed for higher Pr or lower values of Sc. This is due to the fact that fluids with lower Pr give raise to less heat transfer. But the thermal boundary layer thickness increases with increasing Sc.

Figure 1. Local skin-friction at m = 0.5, n = 0.5 and ∆t = 0.01.
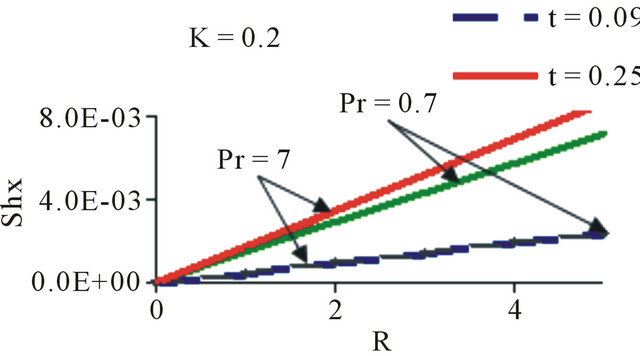
Figure 2. Sherwood number at m = 0.5, n = 0.5 and ∆t = 0.01.
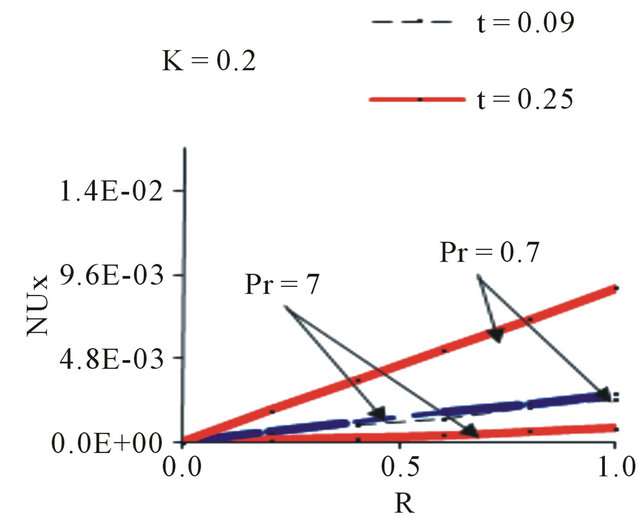
Figure 3. Nusselt number at m = 0.5, n = 0.5, Sc = 0.7 and ∆t = 0.01.

Figure 4. Transient velocity profiles for N = 1, m = 0.5, n = 0.5 and ∆t = 0.01.

Figure 5. Transient concentration profiles for N = 1, m = 0.5, n = 0.5 and ∆t = 0.01.

Figure 6. Transient temperature profiles for N = 1, m = 0.5, n = 0.5 and ∆t = 0.01.

Figure 7. Transient velocity profiles for N = 1, Sc = 0.7, m = 0.5, n = 0.5 and ∆t = 0.01.

Figure 8. Transient concentration profiles for N = 1, Sc = 0.7, m = 0.5, n = 0.5 and ∆t = 0.01.
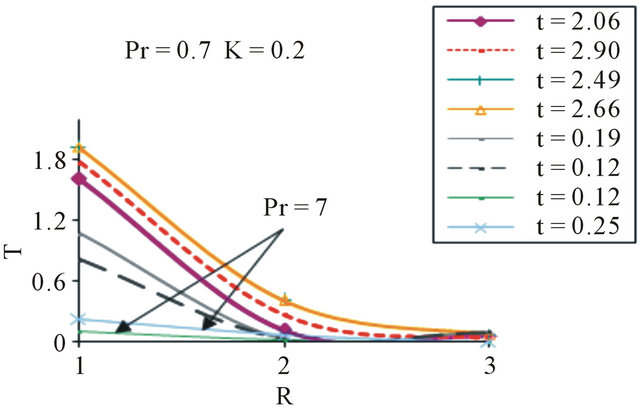
Figure 9. Transient temperature profiles for N = 1, Sc = 0.7, m = 0.5, n = 0.5 and ∆t = 0.01.

Figure 10. Transient concentration profiles for N = 1, Sc = 0.7, m = 0.5, n = 0.5 and ∆t = 0.01.

Figure 11. Transient temperature profiles for N = 1, Sc = 0.7, m = 0.5, n = 0.5 and ∆t = 0.01.

Figure 12. Transient velocity profiles for N = 1, Sc = 0.7, m = 0.5, n = 0.5 and ∆t = 0.01.
The local as well as average skin-friction, Nusselt number and Sherwood number in terms of dimensionless quantities are given by
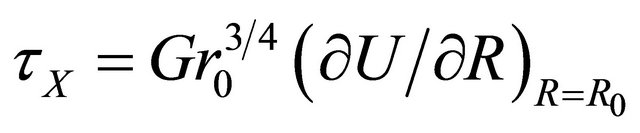 (22)
(22)
 (23)
(23)
 (24)
(24)
 (25)
(25)
 (26)
(26)
 (27)
(27)
The derivatives involved in the Equations (22)-(27) are evaluated using five-point approximation formula and integrals are evaluated using Newton-Cotes formula.
Figures 10 and 12 show that the velocity and the nondimensional concentration distribution decreases as the chemical reaction parameter K increase. The temperature distribution increases as the chemical reaction parameter K increase as in Figure 11.
5. Conclusions
This paper studied the effect of chemical reaction on unsteady natural convection boundary layer flow over a semi-infinite vertical cylinder. Taking into account the buoyancy force effects. The governing equations are solved by an implicit finite difference scheme of CrankNicolson method. The results for the prescribed skin friction, local Nusselt number and the local Sherwood number are presented and discussed. The numerical results indicate that the velocity and the non-dimensional concentration distribution decreases as the chemical reaction parameter increase. The temperature distribution increases as the chemical reaction parameter increase.
Buoyancy ratio parameter has the same effect on concentration profiles as on temperature profiles. Here m has more effect than n. Knowing the velocity and temperature profiles it is customary to study the skin-friction, the rate of heat transfer and mass transfer both in their transient and steady-state conditions. The local Sherwood number exhibits trends that are somewhat different from local skin-friction and Nusselt number. But it increases with an increase in X. With increasing values of Sc larger local Sherwood number is experienced. This is due to the fact that as Sc increases the mass transfer rate increases. Local Sherwood number increases with increasing m or N or decreasing n. This trend is due to fact that concentration profiles decreases with decreasing m or N or increasing n.
List of Symbols
 species concentration;
species concentration;
 dimensionless species concentration;
dimensionless species concentration;
 mass diffusion coefficient;
mass diffusion coefficient;
 acceleration due to gravity;
acceleration due to gravity;
 thermal Grashof number, where
thermal Grashof number, where ;
;
 mass Grashof number;
mass Grashof number;
 thermal conductivity of the fluid, where K = 0.2;
thermal conductivity of the fluid, where K = 0.2;
 mass flux of the diffusing species;
mass flux of the diffusing species;
 exponent in power law variation of the concentration of the wall;
exponent in power law variation of the concentration of the wall;
 combined buoyancy ratio parameter;
combined buoyancy ratio parameter;
 dimensionless average Nusselt number;
dimensionless average Nusselt number;
 dimensionless local Nusselt number;
dimensionless local Nusselt number;
 exponent in power law variation of the wall temperature;
exponent in power law variation of the wall temperature;
Pr Prandtl number;
 rate of heat transfer per unit area;
rate of heat transfer per unit area;
 radial coordinate;
radial coordinate;
 radius of cylinder;
radius of cylinder;
 dimensionless radial coordinate;
dimensionless radial coordinate;
 fourth root of
fourth root of ;
;
 Schmidt number;
Schmidt number;
 dimensionless average Sherwood number;
dimensionless average Sherwood number;
 dimensionless local Sherwood number;
dimensionless local Sherwood number;
 temperature;
temperature;
 dimensionless temperature;
dimensionless temperature;
 time;
time;
 dimensionless time;
dimensionless time;
 velocity components in x, r directions respectively;
velocity components in x, r directions respectively;
 dimensionless velocity components in X, R directions respectively;
dimensionless velocity components in X, R directions respectively;
 axial coordinate measured vertically upward;
axial coordinate measured vertically upward;
 dimensionless axial coordinate.
dimensionless axial coordinate.
Greek Symbols
 thermal diffusivity;
thermal diffusivity;
 volumetric coefficient of thermal expansion;
volumetric coefficient of thermal expansion;
 volumetric coefficient of expansion with concentration;
volumetric coefficient of expansion with concentration;
 dimensionless finite difference grid spacing in R-direction;
dimensionless finite difference grid spacing in R-direction;
 grid size in time;
grid size in time;
 grid size in axial direction;
grid size in axial direction;
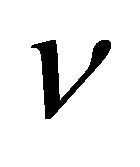 kinematic viscosity;
kinematic viscosity;
 density;
density;
 dimensionless local skin-friction;
dimensionless local skin-friction;
 dimensionless average skin-friction.
dimensionless average skin-friction.
Subscripts
 conditions on the wall;
conditions on the wall;
 free stream conditions.
free stream conditions.
Superscript
 time step level.
time step level.
NOTES