1. Introduction
Dynamic programming (DP) is an important tool in economic dynamics because many models in which a representative agent maximizes a discounted sum of utilities can be treated as a DP problem. In this context, a fixed point of a Bellman operator plays a significant role and fixed point theorems for contraction mappings (Banach [1]) are usually used for this problem (see Le Van [2], Stokey and Lucas [3]). Recently, fixed point theorems of order-type, such as Knaster-Tarski (e.g., Aliprantis and Border [4], Granas and Dugundji [5]), have also been used for this issue (see Kamihigashi [6], Le Van and Vailakis [7]).
This study treats a fixed point theorem of the former. However, the metric we use is different from those in past research. Although most related research uses the uniform norm as the metric, we treat a new metric that corresponds with the topology of uniform convergence on any compact set. Our main results focus on two points. First, we show that there exists a unique fixed point of some operator. Second, we show that the iteration of such an operator results in convergence to this fixed point. This fixed point theorem can be applied Bellman operators in many dynamic economic systems.
The rest of the paper is organized as follows. In the next section, we introduce our framework and state our basic result. In Section 3, we present an application of our theorem to Bellman operators. In the appendix, we give an additional result on our metric.
2. Framework and Basic Results
Let X be a Hausdorff space and suppose that there exists an increasing sequence 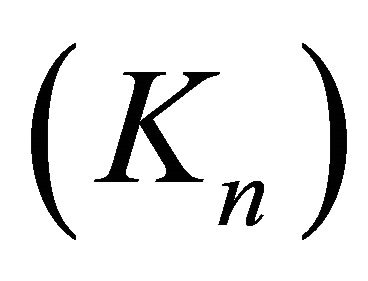 of compact sets in X such that1
of compact sets in X such that1
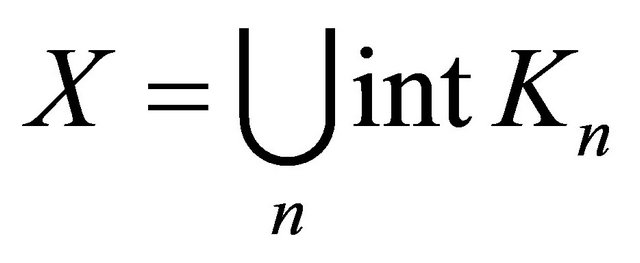
For any real-valued functions 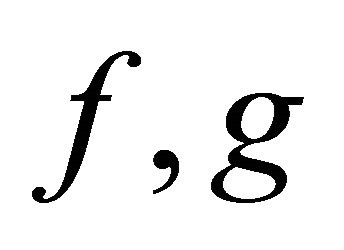 on
on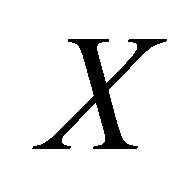 , let
, let

and let  be the set of all functions such that
be the set of all functions such that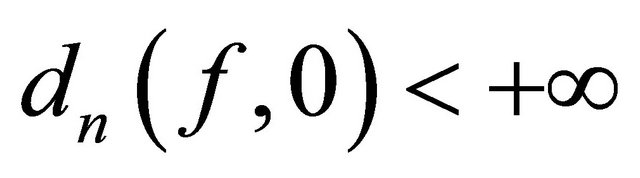 . Then
. Then 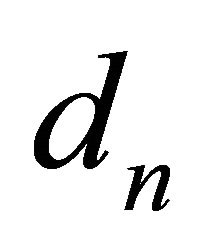 is a pseudo-metric on
is a pseudo-metric on . Define
. Define
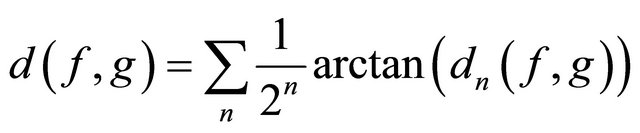
for any 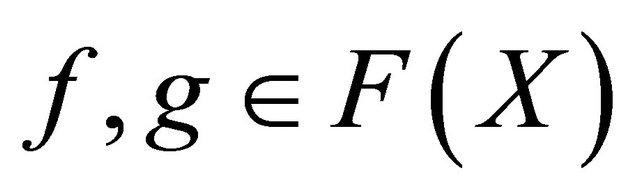 and d is a metric of
and d is a metric of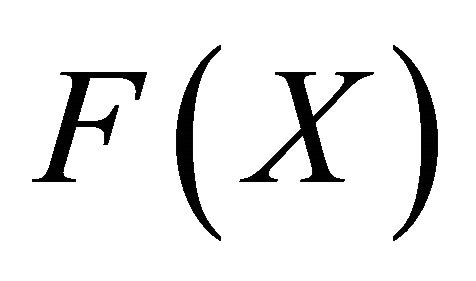 . In the Appendix, we will verify that, for any sequences
. In the Appendix, we will verify that, for any sequences 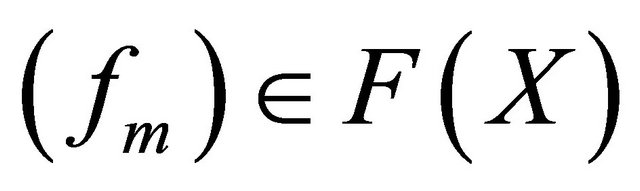 and
and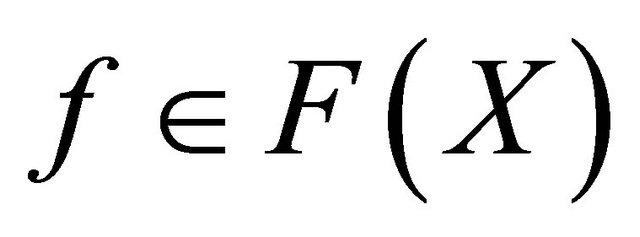 ,
, 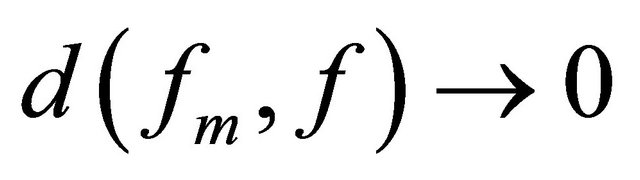 if and only if
if and only if 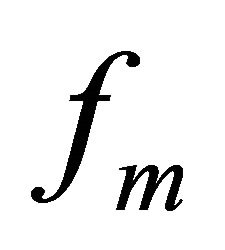 converges to f uniformly on any compact subset of X.
converges to f uniformly on any compact subset of X.
The following theorem holds.
Theorem 1: Suppose that  satisfies the following two conditions:
satisfies the following two conditions:
1) For any  and any
and any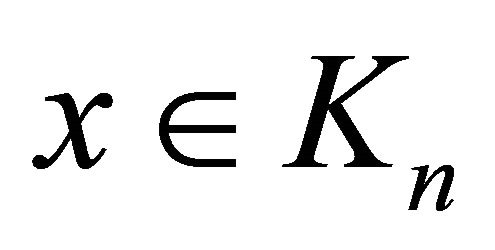 ,
, 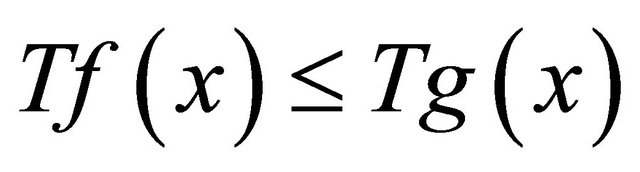 if
if 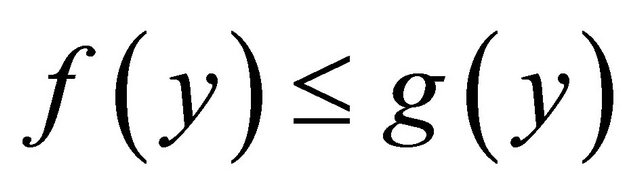 for any
for any ;
;
2) There exists  such that, for any
such that, for any 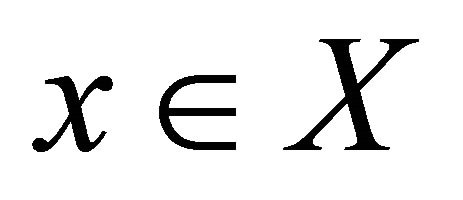
and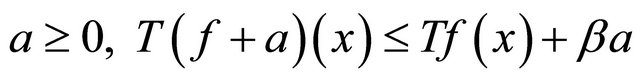 .
.
Choose any  and define
and define 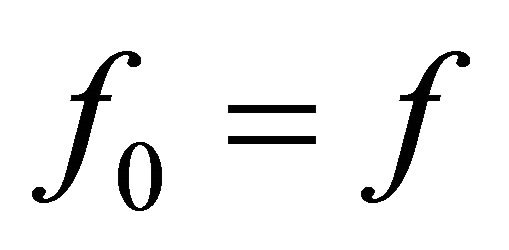 and
and 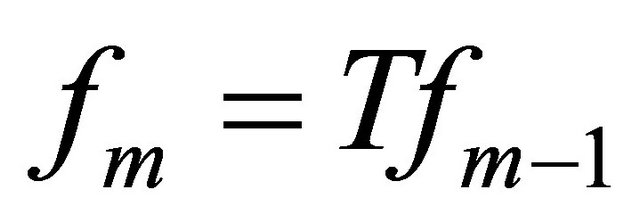 for any
for any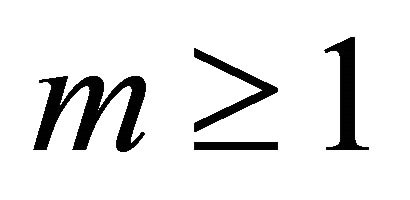 . Then
. Then 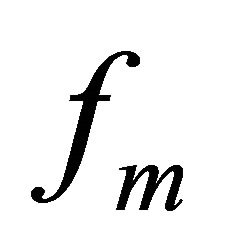 converges to a unique fixed point
converges to a unique fixed point 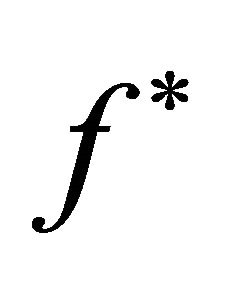 of
of 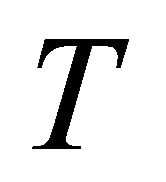 with respect to d.
with respect to d.
Proof: Choose any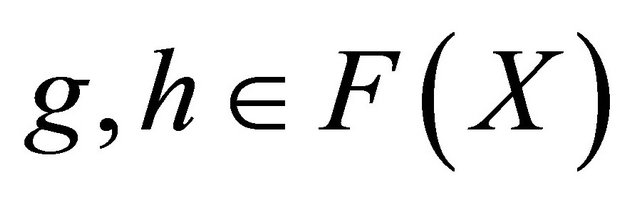 . By definition of
. By definition of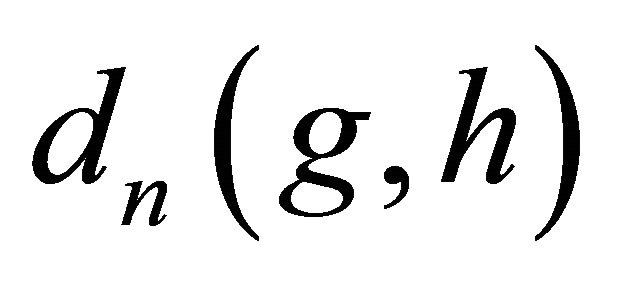 , we have
, we have

for any . By (1) and (2),
. By (1) and (2),
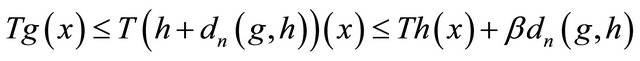
Hence, we have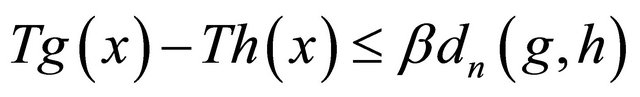 . By symmetry, we can verify that
. By symmetry, we can verify that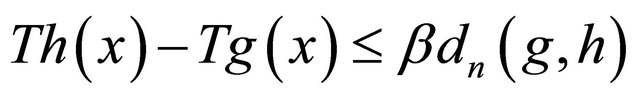 . Thus,
. Thus,
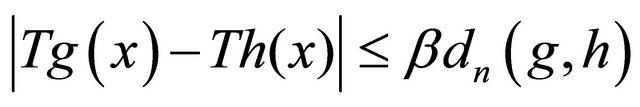
for all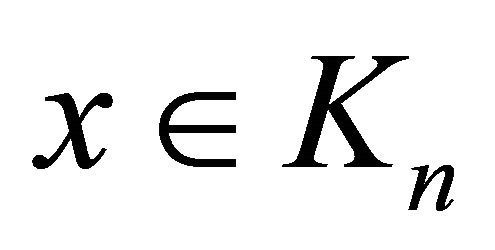 , and hence
, and hence
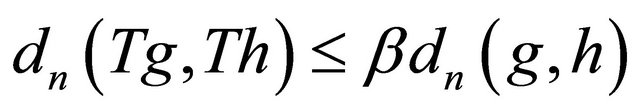
for any $n$. Therefore, if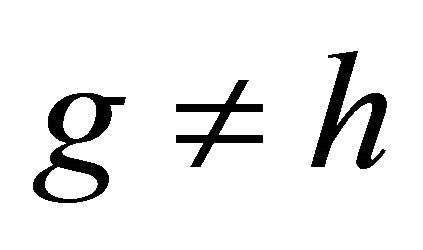 ,
,

If 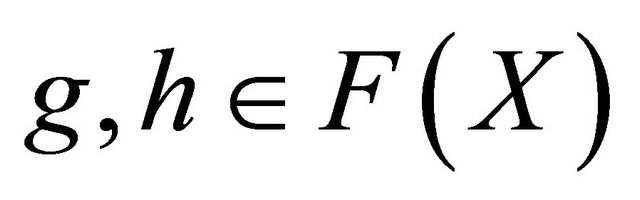 are two distinct fixed points of T, then
are two distinct fixed points of T, then
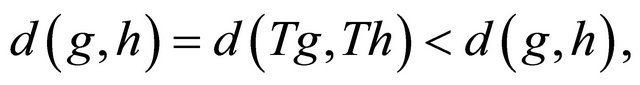
which is a contradiction. Thus, T has at most one fixed point2.
Next, for any 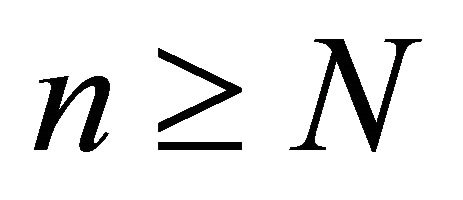 and
and ,
,

Therefore, if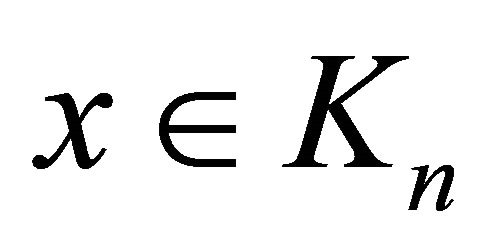 , then
, then
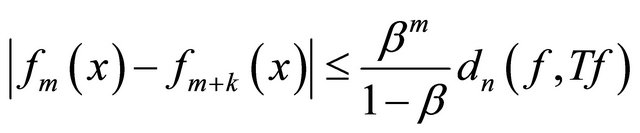
and thus 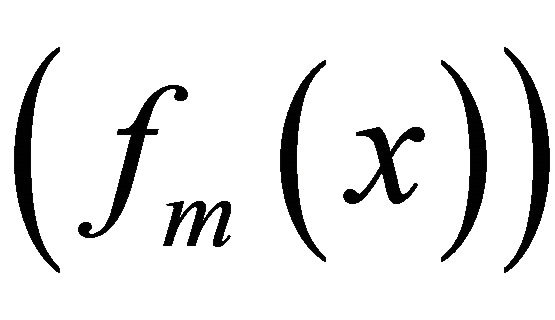 is a Cauchy sequence. Hence,
is a Cauchy sequence. Hence,  converges to some real number denoted by
converges to some real number denoted by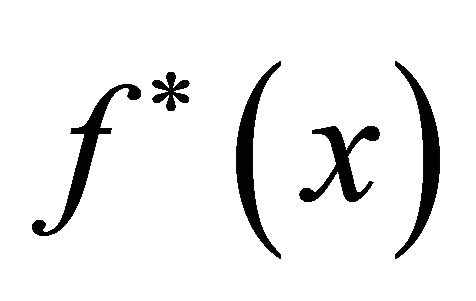 . Then
. Then
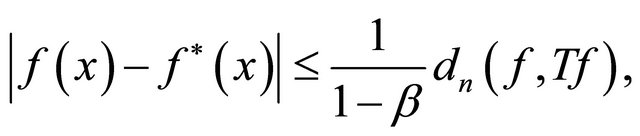
and thus
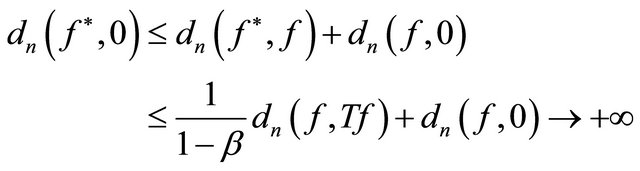
Hence, the function 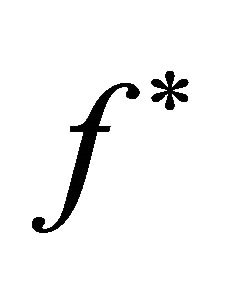 is in
is in .
.
Now, for any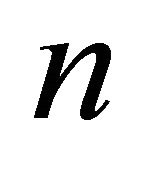 ,
,
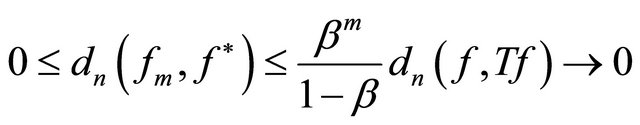
as , and thus
, and thus 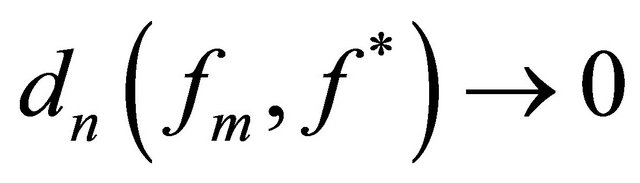 for any
for any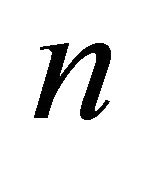 . Choose any
. Choose any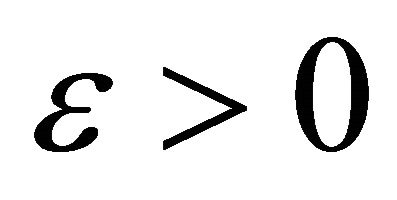 , and choose any
, and choose any 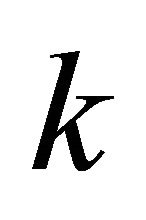 such that
such that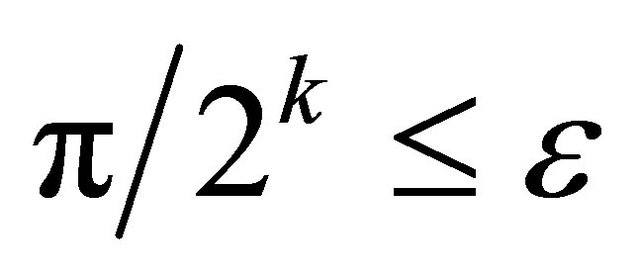 . We have already shown that, for any sufficiently large
. We have already shown that, for any sufficiently large ,
,
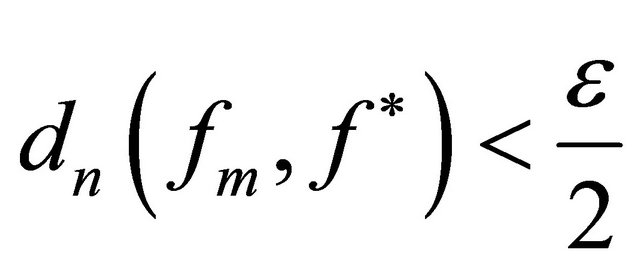
for all . Then3
. Then3
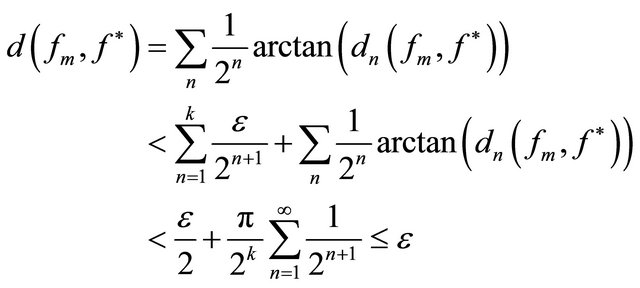
and thus .
.
Now, T is a Lipschitz function on d and is thus continuous. Hence,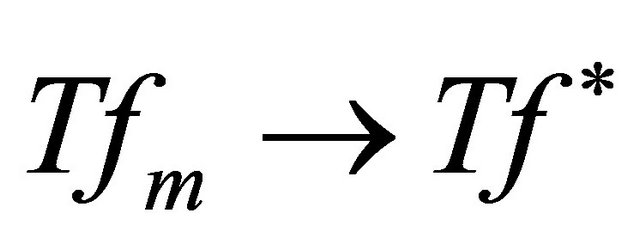 . Meanwhile, since
. Meanwhile, since  ,
,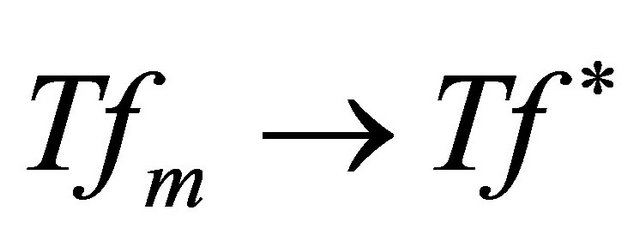 . Thus
. Thus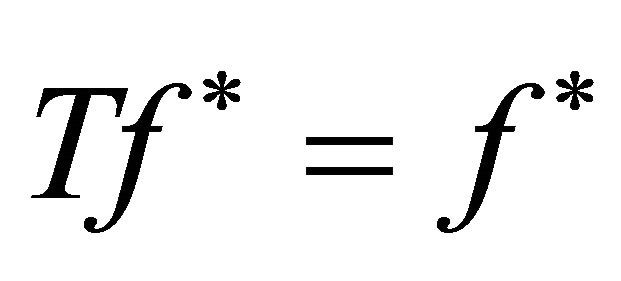 , and so f* is a fixed point of T. This completes the proof.
, and so f* is a fixed point of T. This completes the proof.
3. Application to Bellman Operators
Let 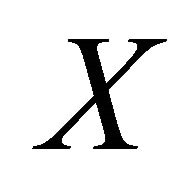 be a Hausdorff space, let
be a Hausdorff space, let  be a correspondence from
be a correspondence from 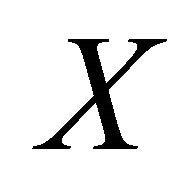 into
into 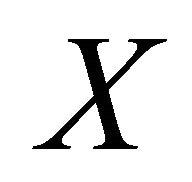 and let
and let 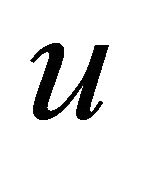 be a real-valued function on
be a real-valued function on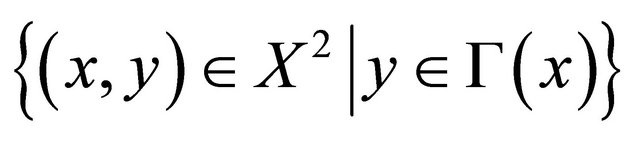 , and define
, and define
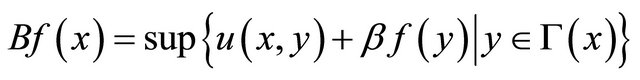 .
.
We call the operator B a Bellman operator. Consider the following problem:

Let  denote the maximum value for the above problem. It is well-known that under several conditions,
denote the maximum value for the above problem. It is well-known that under several conditions, 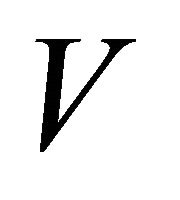 is a fixed point of the Bellman operator.
is a fixed point of the Bellman operator.
Then we can show the following theorem.
Theorem 2: Suppose that 1) 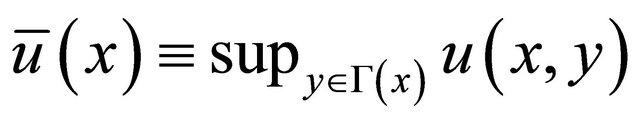 is real-valued and continuous on
is real-valued and continuous on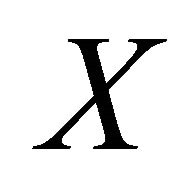 ;
;
2) 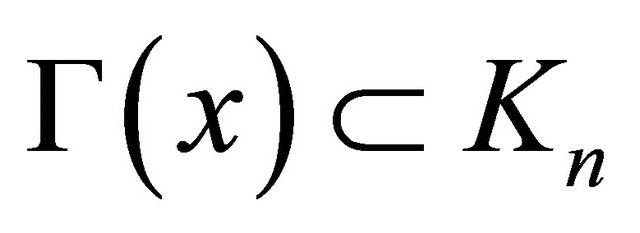 for any
for any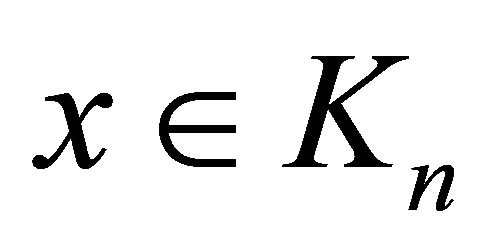 .
.
Then 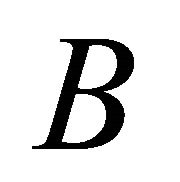 is a mapping from
is a mapping from 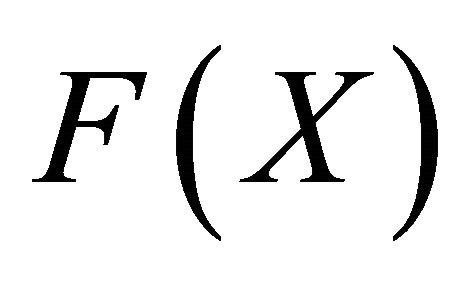 into
into . Further, for any
. Further, for any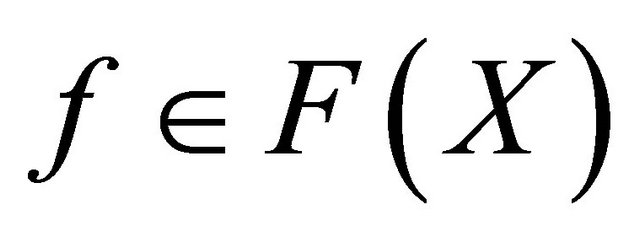 , if
, if 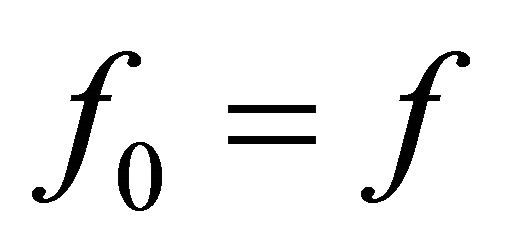 and
and 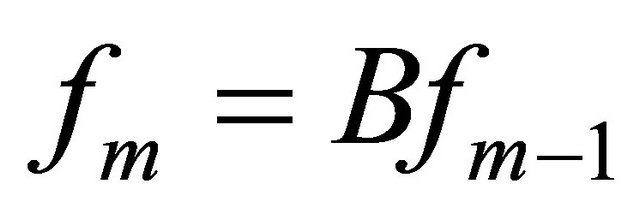 for any
for any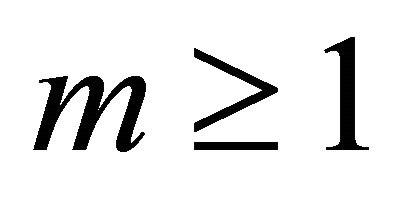 , then
, then 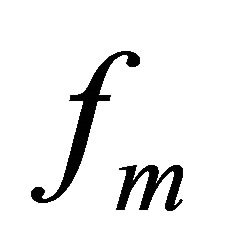 converges to a unique fixed point of
converges to a unique fixed point of 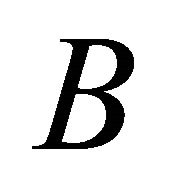 with respect to
with respect to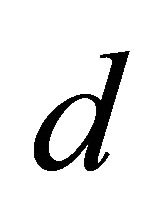 .
.
Note that the conditions of Theorem 2 are not so strict. In many economic models, the following conditions are satisfied:
1)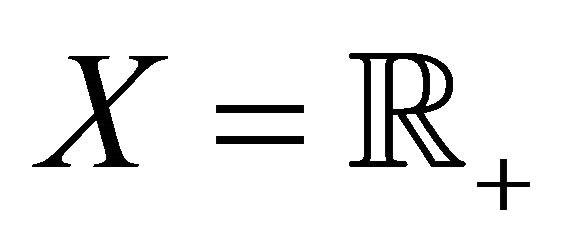 ;
;
2) There exists  such that, if
such that, if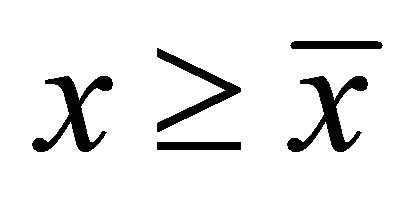 , then
, then 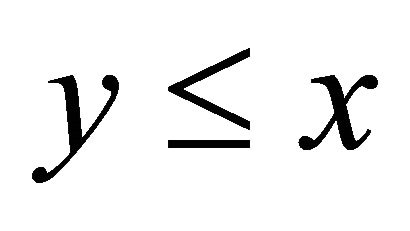 for any
for any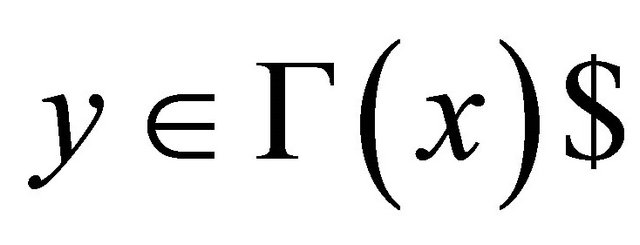 ;
;
3) For any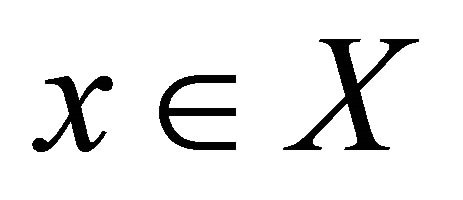 ,
,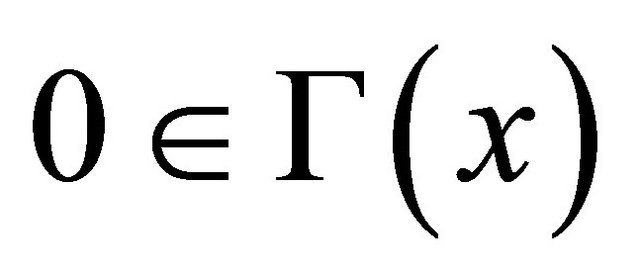 ;
;
4) 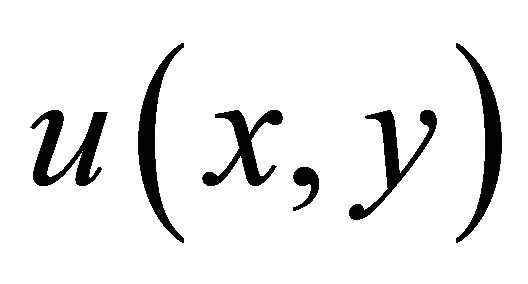 is non-increasing in
is non-increasing in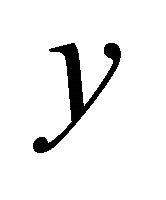 ;
;
5) 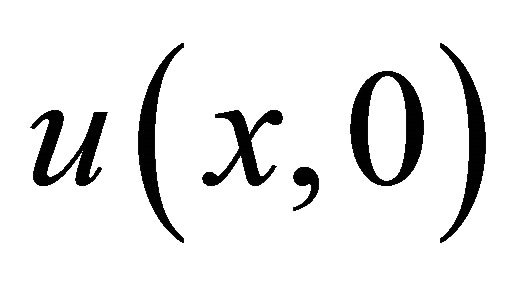 is continuous in
is continuous in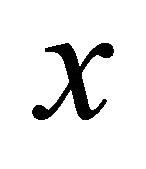 .
.
Under these conditions, we can show that 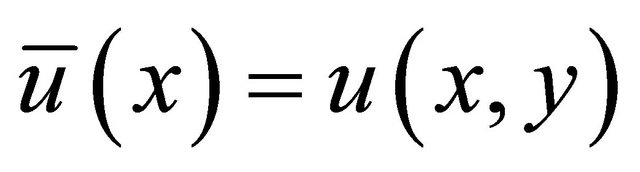 , and thus condition 1) of Theorem 2 is satisfied. Also, by setting
, and thus condition 1) of Theorem 2 is satisfied. Also, by setting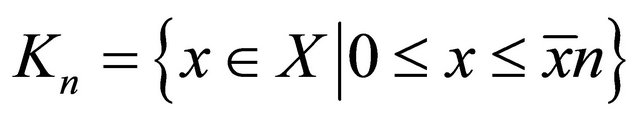 , condition 2) of Theorem 2 is satisfied. Hence Theorem 2 is applicable.
, condition 2) of Theorem 2 is satisfied. Hence Theorem 2 is applicable.
Proof: By 2), B satisfies 1) and 2) of Theorem 1. Hence, it suffices to show that B is a mapping from 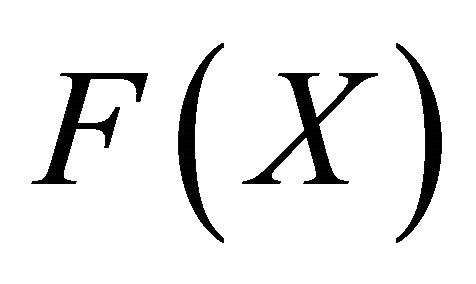 into
into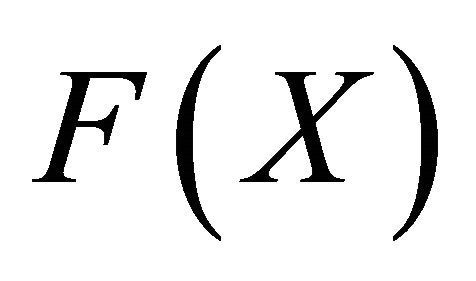 . By 1), we have
. By 1), we have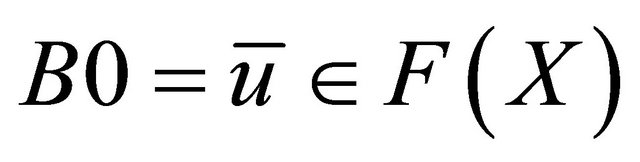 . Choose any
. Choose any . As in the proof of Theorem 1, we can show that
. As in the proof of Theorem 1, we can show that
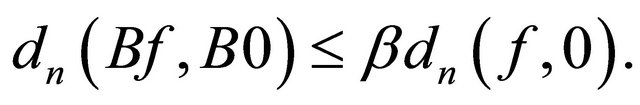
Then

which implies that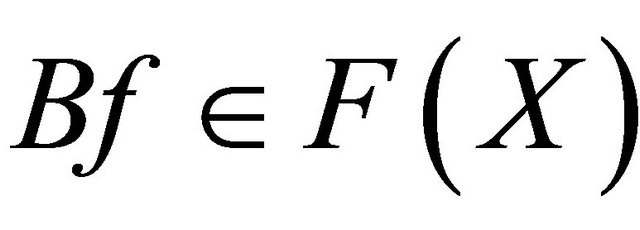 . This completes the proof. □
. This completes the proof. □
4. Conclusion
In this paper, we introduced a new fixed point theorem and showed that it can be applied to the Bellman operator of several economic models. The claim of our theorem includes not only the existence of fixed point but also the convergence result on iteration. By using our result, one can get value function from iterative application of the Bellman operator in a wide class of dynamic economic models.
5. Acknowledgements
The authors are grateful to Hiroyuki Ozaki for his helpful comments and suggestion. This research is partially supported by Keio/Kyoto Joint Global Center of Excellence Program Raising Market Quality-Integrated Design of “Market Infrastructure”.
Appendix. Additional Notes on Our Metric
Theorem A: Suppose 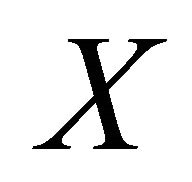 satisfies the assumption in Section 2 and we define
satisfies the assumption in Section 2 and we define  as in Section 2. Suppose also that
as in Section 2. Suppose also that 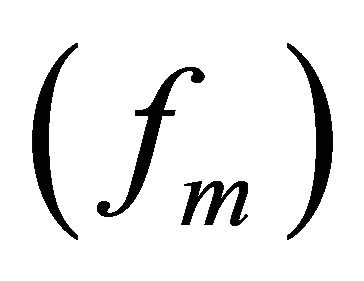 is a sequence in
is a sequence in 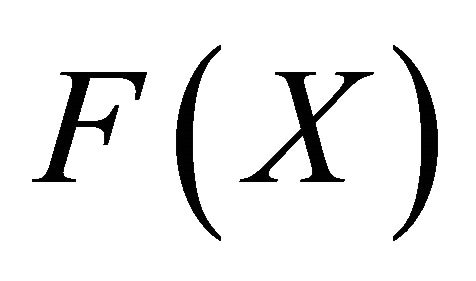 and that
and that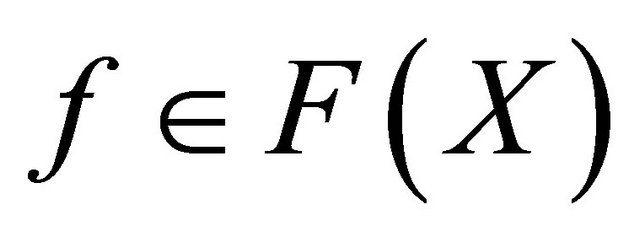 . Then
. Then 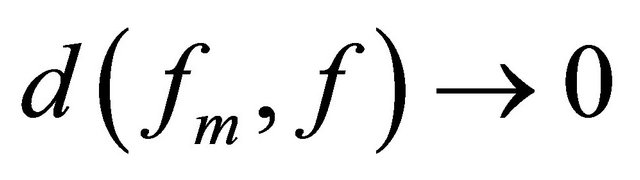 if and only if
if and only if

for any compact set .
.
Proof of Theorem A: If the latter holds, then we have 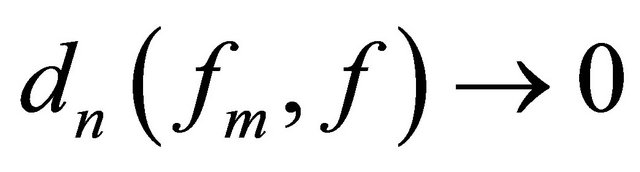 for any
for any . Therefore,
. Therefore,
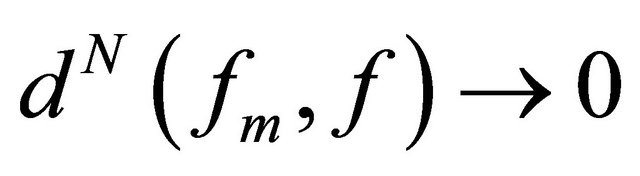 .
.
Conversely, suppose that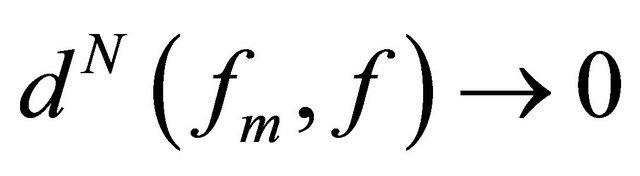 . For any compact set
. For any compact set ,
, 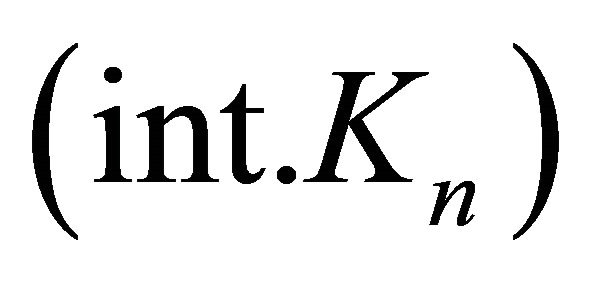 is an open covering of
is an open covering of , and thus there exist
, and thus there exist  such that
such that

Since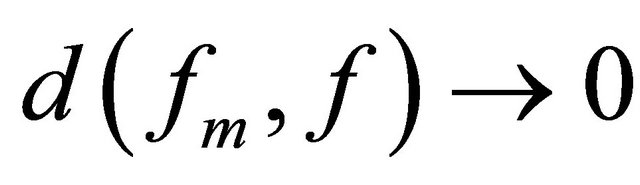 , we have
, we have . Therefore,
. Therefore,
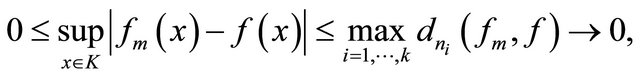
which completes the proof. □
NOTES
1Such a sequence exists if X is locally compact and second countable.
2Let 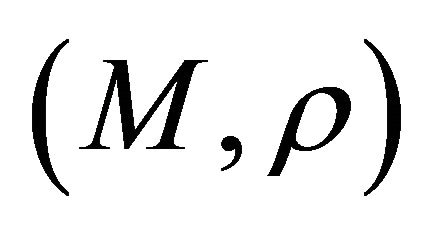 be a metric space. A mapping
be a metric space. A mapping 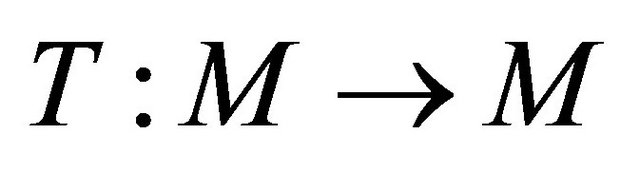 is said to be contractive (strictly contractive) if
is said to be contractive (strictly contractive) if 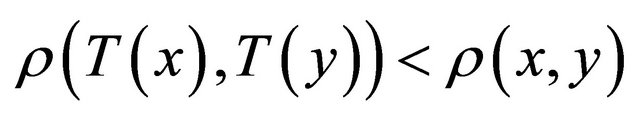 for each
for each  with
with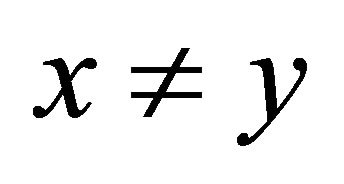 . In our result, we use this mapping, but the following well-known result (for a detailed argument, see Goebel and Kirk [8], Kirk [9]) is not applicable since it assume a compact metric space.
. In our result, we use this mapping, but the following well-known result (for a detailed argument, see Goebel and Kirk [8], Kirk [9]) is not applicable since it assume a compact metric space.
Theorem: Let  be a compact metric space and let
be a compact metric space and let 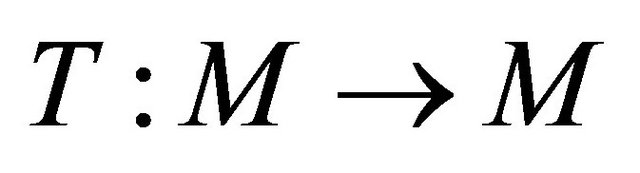 be a contractive mapping. Then
be a contractive mapping. Then  has a unique fixed point
has a unique fixed point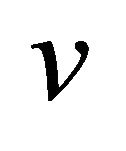 , and moreover, for each
, and moreover, for each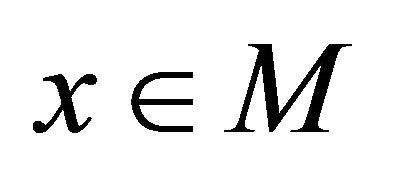 ,
, .
.
3Note that 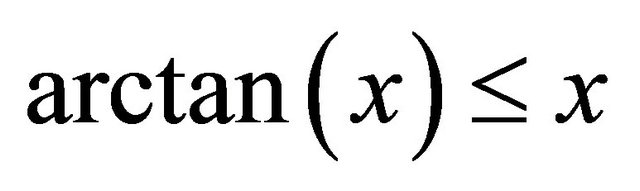 for any
for any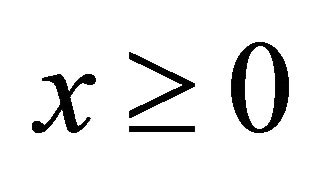 .
.