Eliciting Probabilities, Means, Medians, Variances and Covariances without Assuming Risk Neutrality ()
1. Introduction
The economic literature on the elicitation of an expert’s subjective beliefs has focused on so-called proper scoring rules. These mechanisms, which are used in many economic experiments, reward the expert on the basis of post-elicitation events such that it is in the expert’s interest to report her true beliefs if she is risk neutral. The quadratic scoring rule (QSR) [1] is the most popular rule, used to elicit the probability of an event or the mean of a random variable. In the absence of risk neutrality, there is an incentive to report conservative beliefs in order to avoid large losses [2]. This is a problem, since risk neutrality is shown to be widely violated in experimental studies [e.g. 3]. Indeed, Armantier and Treich [4] show experimentally that consistent with risk aversion, elicitation with the quadratic scoring rule leads to conservative bias in reported beliefs.
There are different ways to get around this problem. Offerman et al. [5] propose a way to correct for deviations of risk neutrality and expected utility, by quantifying the size of deviations for each individual. Alternatively, an earlier literature starting with Smith [6]1 shows how one can induce risk neutrality by rewarding subjects using binary lottery tickets. This idea has been used to show how to elicit the subjective probability of an event [e.g. 10,11] in a way similar to the elicitation of a reservation price [12].
We extend this literature in several ways. First, we prove that deterministic schemes are not adequate if one does not know the risk preferences of the expert. Second, we combine the literature on scoring rules for risk neutral preferences with the literature on incentivizing with lottery tickets to show that one can elicit a median or any quantile without making assumptions on risk preferences. We also present an alternative way to elicit a probability or mean based on the randomized quadratic scoring rule. Third, we present a new deterministic rule, and its randomized counterpart, to elicit variances and covariances when two independent observations are available.
2. Preliminaries
We consider two people, an expert and an elicitor. The expert has subjective beliefs about the distribution  of a bounded random variable
of a bounded random variable  that yields outcomes belonging to
that yields outcomes belonging to  with
with . The expert maximizes expected utility for some utility function
. The expert maximizes expected utility for some utility function  on
on  such that
such that 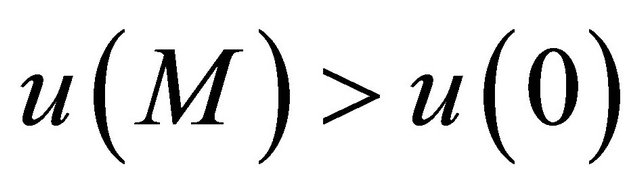 for some
for some . The elicitor only knows that
. The elicitor only knows that 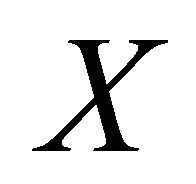 yields outcomes belonging to
yields outcomes belonging to , and would like to learn some parameter
, and would like to learn some parameter  of the distribution
of the distribution . We consider the use of a reward system or scoring rule
. We consider the use of a reward system or scoring rule  which rewards the expert on the basis of her report
which rewards the expert on the basis of her report  and a single random realization
and a single random realization  of
of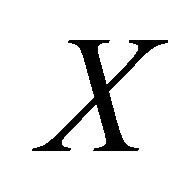 . Here,
. Here,  is a distribution over the rewards which includes a deterministic reward as a special case. In the literature,
is a distribution over the rewards which includes a deterministic reward as a special case. In the literature, 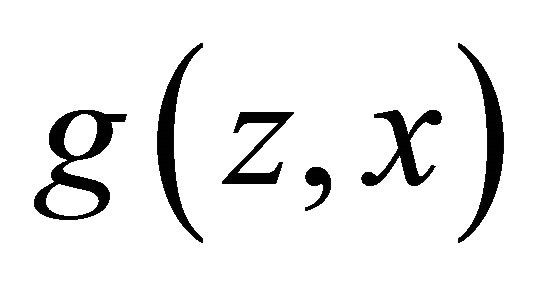 is called strictly proper for
is called strictly proper for  if
if
 for all
for all . We say that a rule elicits
. We say that a rule elicits  if
if  for all
for all  and all
and all  with
with .
.
3. Limitations of Deterministic Rewards
Consider an elicitor who wishes either to learn about the mean of some random variable 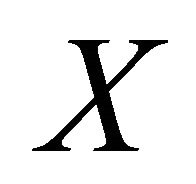 with support in
with support in , or about probability of some event
, or about probability of some event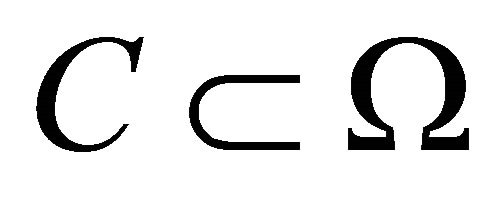 . We obtain the following result.
. We obtain the following result.
Proposition 1. A scoring rule with a deterministic reward cannot elicit the probability  or the mean
or the mean .
.
The proof is in the Appendix. The intuition is simple. The elicitor has only one parameter, the realization , to incentivize the expert to tell the truth. On the other hand, there are two dimensions of uncertainty as the elicitor does not know
, to incentivize the expert to tell the truth. On the other hand, there are two dimensions of uncertainty as the elicitor does not know  and
and 
4. Probabilistic Elicitation
We now consider elicitation using probabilistic or randomized reward functions. The idea, first elaborated by Smith [6], is that one pays the experts in lottery tickets rather than money. The size of the prize is given by the probability of winning the lottery. Hence  where
where 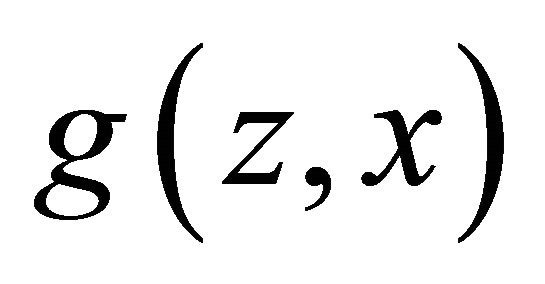 is now the payoff distribution awarded conditional on
is now the payoff distribution awarded conditional on . Using this idea, we show how to elicit probabilities, means, different quantiles, and variances and covariances.
. Using this idea, we show how to elicit probabilities, means, different quantiles, and variances and covariances.
4.1. Randomization Trick
We use the following “randomization trick” to transform deterministic into probabilistic payoffs. First, given a deterministic reward function , determine
, determine  and
and 
such that  and
and 
Second, draw a realization  from a uniform distribution on
from a uniform distribution on  and then pay
and then pay  if
if  and pay
and pay  if
if 
Formally, we replace the deterministic reward  by the randomized reward
by the randomized reward

where 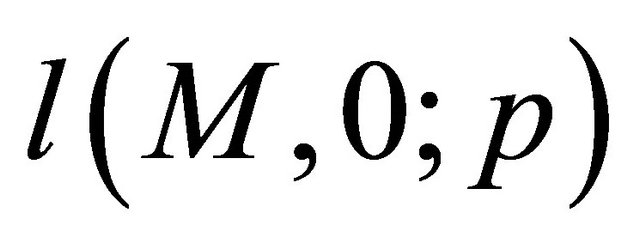 is a lottery that pays
is a lottery that pays 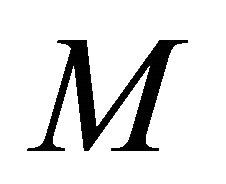 with probality
with probality 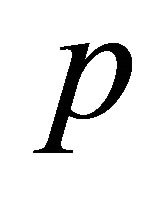 and
and 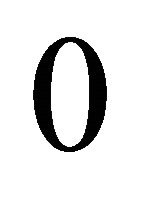 with probability
with probability  Consequently,
Consequently,

The expected utility of the expert equals an affine transformation of . Thus, a report that maximizes her expected utility is a report that maximizes the utility of a risk neutral expert and vice versa. In particular,
. Thus, a report that maximizes her expected utility is a report that maximizes the utility of a risk neutral expert and vice versa. In particular,  elicits
elicits  iff
iff  is strictly proper for
is strictly proper for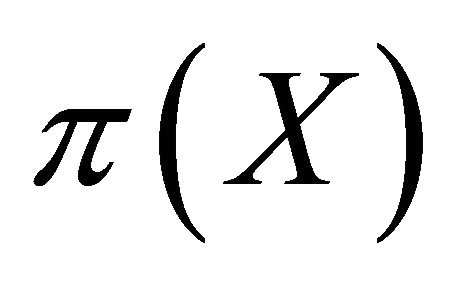 .2
.2
4.2. Eliciting Probabilities
Randomized rewards for the elicitation of probabilities have received quite some attention. Grether [10] (see also Holt [15, ch. 30] and Karni [16]) presents a simple reward function where a prize is rewarded with some probability that depends on the draw of two uniformly distributed random variables. Allen [11] presents an alternative rule that relies on a draw of a random variable that has a more complex probability distribution. Mclvey and Page [17] uses a randomized version of the quadratic scoring rule in an experimental application, which is similar to the rule we present below.
The QSR (for the event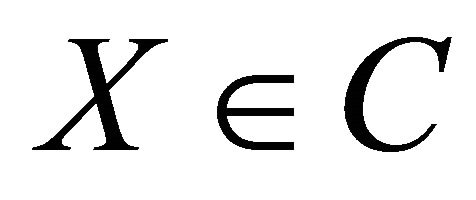 ) is given by
) is given by

and is strictly proper for  [1]. The randomized quadratic scoring rule (for the event
[1]. The randomized quadratic scoring rule (for the event ), short rQSR, is defined by
), short rQSR, is defined by
 The following result obtains:
The following result obtains:
Proposition 2. The randomized quadratic scoring rule elicits .
.
Note that the expected payoffs under rQSR are identical to those under the rules of Allen [11] and McKelvey and Page [17] when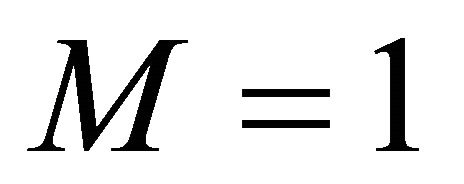 .
.
4.3. Eliciting the Mean
To elicit the mean, we combine the randomization trick with the fact that the QSR  is a strictly proper scoring rule for the mean (for risk neutral experts). Given
is a strictly proper scoring rule for the mean (for risk neutral experts). Given 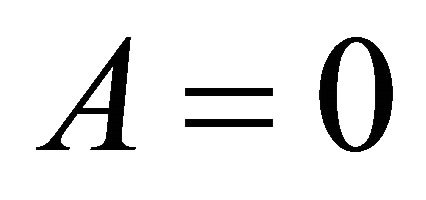 and
and  we obtain the randomized quadratic scoring rule as defined by
we obtain the randomized quadratic scoring rule as defined by
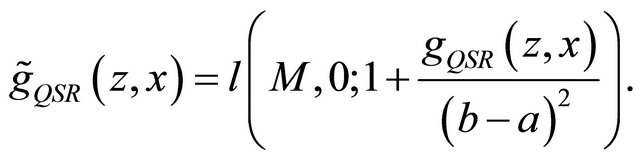
Proposition 3. The randomized quadratic scoring rule elicits .
.
4.4. Median and Quantiles
The quantile scoring rule, due to Cervera and Munoz [18] is a strictly proper scoring rule for the quantile 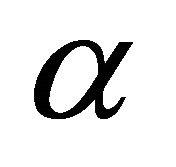 of the distribution
of the distribution  of
of  for any given
for any given . Its reward function is given by
. Its reward function is given by  The randomized quantile scoring rule is hence given by
The randomized quantile scoring rule is hence given by  where
where
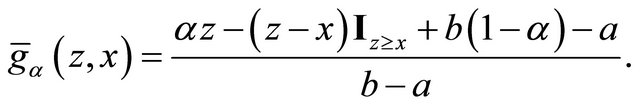
Proposition 4. The randomized quantile scoring rule elicits the quantile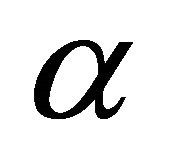 .
.
In particular, Proposition 4 shows how to elicit the median by setting .
.
4.5. Variance and Covariance
In order to elicit the variance of 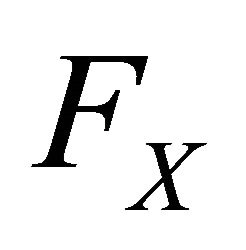 we assume the elicitor can condition on two independent realizations
we assume the elicitor can condition on two independent realizations  and
and  of
of  when rewarding the expert. So we conder a reward function
when rewarding the expert. So we conder a reward function 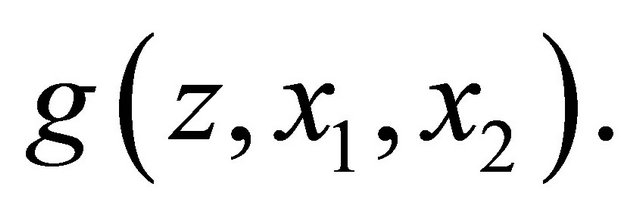 We first construct a strictly proper scoring rule. Following Walsh (1962),
We first construct a strictly proper scoring rule. Following Walsh (1962),
 where
where 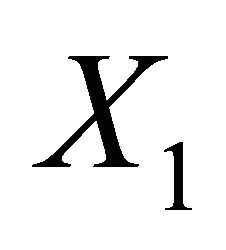 and
and  are indendent copies of
are indendent copies of  We combine this with the quadratic scoring rule to obtain that the variance scoring rule
We combine this with the quadratic scoring rule to obtain that the variance scoring rule 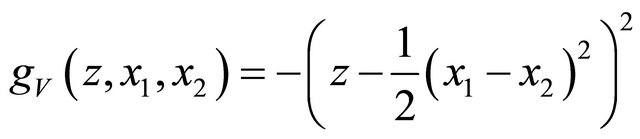 that is strictly proper for
that is strictly proper for 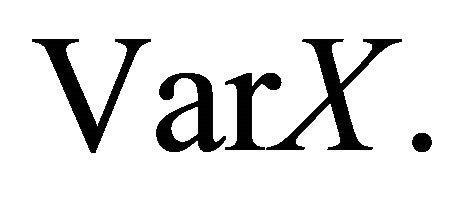 Given
Given
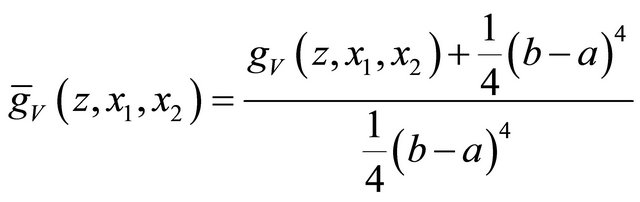
we obtain the randomized variance scoring rule by

Proposition 5. The randomized variance scoring rule elicits the variance of 
Similarly we can elicit the covariance given two ranm variables  and
and  We assume that
We assume that 
for  Here we condition on a realization
Here we condition on a realization  drawn from
drawn from  Again following Walsh (1962)we use the fact that
Again following Walsh (1962)we use the fact that 
and then use the QSR to define the covariance scoring rule 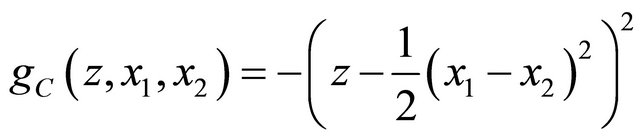 that is strictly proper for
that is strictly proper for  Given
Given  and
and
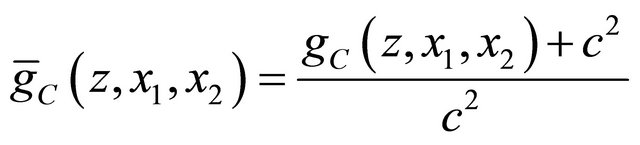
we obtain the randomized covariance scoring rule by

Proposition 6. The randomized covariance scoring rule elicits the covariance of 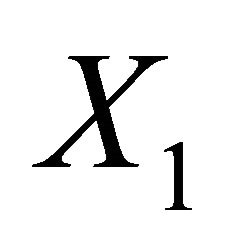 and
and 
5. Conclusions
We have rigorously shown the limits of deterministic scoring rules for belief elicitation. To overcome those limitations, we applied the idea of paying in lottery tickets to transform known deterministic scoring rules for belief elicitation, such as the well-known QSR, into randomized rules. These rules provide agents with incentives to truthfully report parameters of a subjective probability distribution for all risk preferences, and can be used in experimental applications.
This paper has considered the theoretical side. On the empirical side, it is an open question whether these rules have the desired properties in actual applications, and how they are best presented to subjects. Selten et al. [19, see also review therein] raises doubt whether subjects rewarded using lotteries behave as if risk neutral in experiments. More recently, Harrison et al. [14,20], and Hossain and Okui [13] provide evidence that the produre can induce subjects to behave more in line with risk neutrality.
Appendix
Proof of Proposition 1. If one can elicit the mean of a random variable for all distributions in  then one can also elicit the probability of an event as
then one can also elicit the probability of an event as 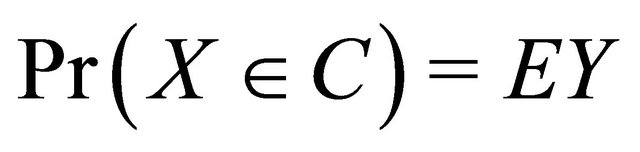 if
if  is the Bernoulli random variable such that
is the Bernoulli random variable such that 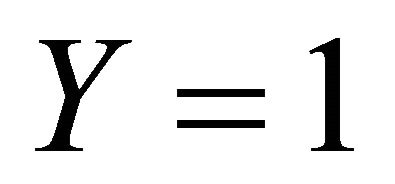 if and only if
if and only if  Hence it is enough to show that one cannot elicit
Hence it is enough to show that one cannot elicit 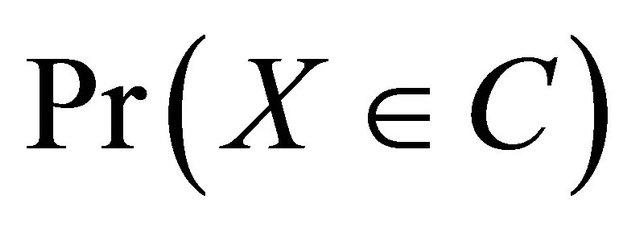 to prove that one cannot elicit
to prove that one cannot elicit 
We first show that 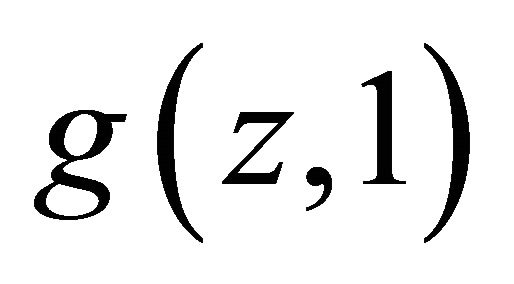 and
and 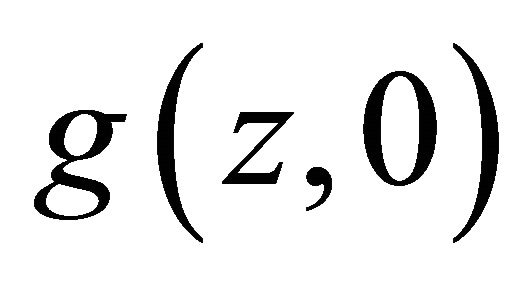 are differentiable almost everywhere. Once this is established the first order conditions reveal the impossibility.
are differentiable almost everywhere. Once this is established the first order conditions reveal the impossibility.
Consider 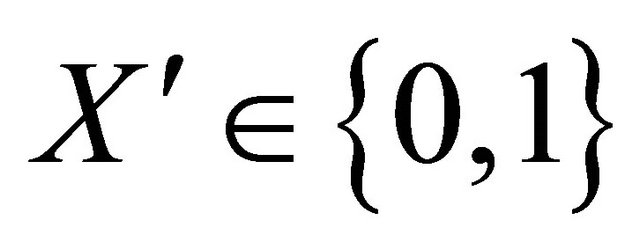 where
where  So
So
 Let
Let 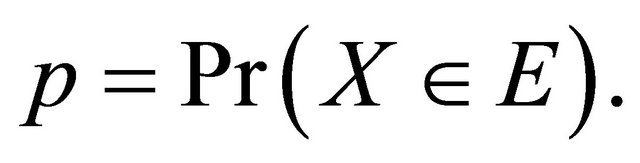
Assume that 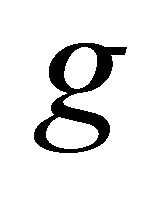 elicits
elicits  for all concave
for all concave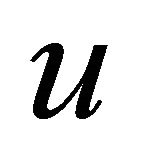 . Then we have for all
. Then we have for all 
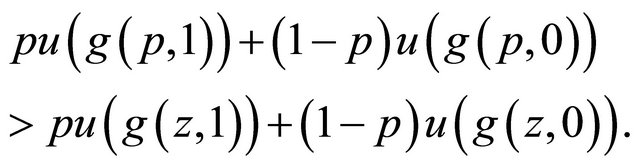
For  and
and  we have
we have

so

so

Hence we have shown that 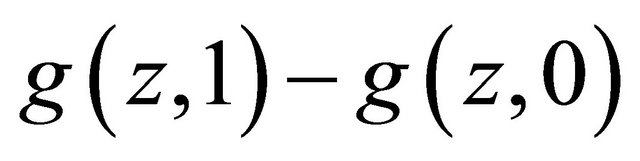 is strictly increasing in
is strictly increasing in 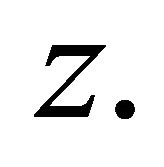
Similarly, for  we have
we have

and since

it follows that  So
So  strictly decreasing in
strictly decreasing in  and hence
and hence 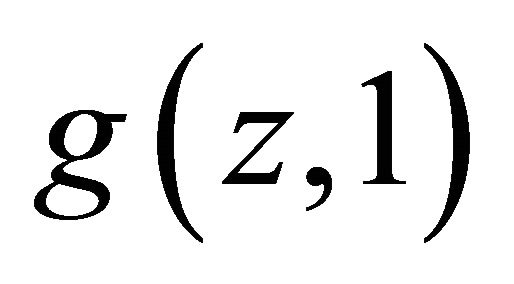 is strictly increasing.
is strictly increasing.
From the above two strict monotonicity statements we obtain that  and
and  are differentiable almost everywhere. Let
are differentiable almost everywhere. Let  be the set where they are differentiable.
be the set where they are differentiable.
For  and differentiable
and differentiable  we can calculate
we can calculate

and infer that
 (1)
(1)
It is easy to argue with generalized version of the intermediate value theorem that there is  such that
such that  Consider
Consider 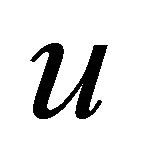 that is differentiable with
that is differentiable with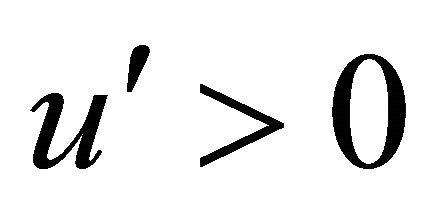 . Then rewrite (1) as:
. Then rewrite (1) as:
 (2)
(2)
Since  is strictly increasing in
is strictly increasing in  there is some
there is some 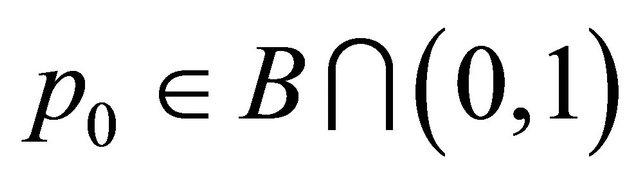 such that
such that
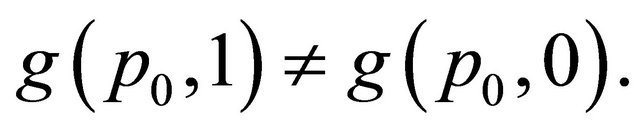 So when
So when 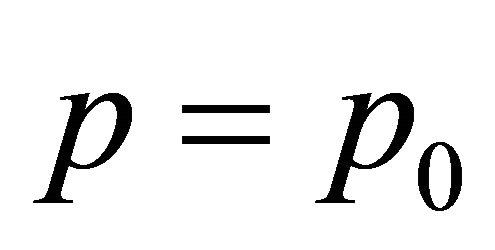 the left hand side of (2) depends on
the left hand side of (2) depends on . Therefore, (2) cannot hold for all
. Therefore, (2) cannot hold for all .
.
NOTES
2Other authors have independently worked on similar mechanisms. Hossain and Okui [13] presents a randomized mechanism for eliciting the mean of a symmetric distribution, allowing for unbounded support with some additional restrictions. Harrison et al. [14] considers a version of the rQSR (see below), which they call the Binary Lottery Procedure. Both papers also consider non-expected utility theory.