Evolutionarily Stable Conjectures and Social Optimality in Oligopolies ()
1. Introduction
The theory of Conjectural Variations (CV) has witnessed several important developments since its origins in the industrial organization literature approximately a century ago (Bowley (1924) [1] and Frisch (1933) [2]). The CV of a firm in an oligopoly market is defined as the firm’s perception or belief regarding the reaction of its rival firms to changes in its quantity (or output) decision1. CV was initially conceptualized in static games with complete information and rational players (Bresnahan (1981) [3]), and thereafter in dynamic games with complete information and rational players (Dockner (1992) [4]).
Bresnahan (1981) [3] introduced the notion of Consistent Conjectural Equilibrium (CCE) in static games, where the reaction functions of firms and their conjectures coincide (in equilibrium), thus “endogenising” the concept of CV2. Breshnahan showed that under the assumptions of constant marginal costs, linear demand and perfect substitutability in oligopolies, the Bertrand equilibrium is a CCE, but the Cournot equilibrium is not.
While the idea of consistent conjectures in static games brought in notions of rationality, the concept of reactions of a firm to the actions of the rival firm is dynamic in nature. Dockner (1992) [4] attempted to understand the relationship between dynamic oligopolistic competition and static conjectural variations equilibria, by comparing the long-run equilibrium of a dynamic oligopoly game to the conjectural variations equilibrium of the corresponding static game.
Dockner showed that the long-run “open-loop” equilibrium of the dynamic game coincides with the Cournot equilibrium of the corresponding static game, while the long-run ‘closed-loop’ equilibrium of the dynamic game coincides with the conjectural variations equilibrium of the corresponding static game3. Thus, the static conjectural variations approach can be viewed as the limit of dynamic strategic interactions in oligopolies.
Despite the attempts to rationalize the inclusion of CV in oligopoly models with the aid of dynamic games, many controversies still exist. The theoretical foundation based on complete information and full rationality is considered weak. Thus, during the last two decades, CV has been examined in dynamic games with incomplete information and boundedly rational players.
For instance, Itaya and Dasgupta (1995) [5] developed the first learning model of CV, where players can revise their conjectures based on past observations in a dynamic game. Similarly, Friedman and Mezzetti (2002) [6] developed an incomplete information game with boundedly rational players. Based on the above two analyses, Jean-Marie and Tidball (2002) [7] modeled a learning process where each player has a linear conjecture of the other player’s behavior.
Dixon and Somma (2003) [8], Muller and Norman (2005) [9] and Possajennikov (2009) [10] employed an evolutionary game-theoretic framework to characterize CV using the notion of Evolutionarily Stable Strategies (ESS), first introduced by Maynard Smith (1982) [11]. ESS is defined as the Nash equilibrium strategy in an evolutionary game, which is stable in the sense that (a) it is the best response against itself in the population and (b) once it is fixed, no alternative strategy can invade the population successfully.
The above authors independently derive ESS for an evolutionary game involving a duopoly. They show that ESS coincides with the consistent CV of the static duopoly game, as defined by Bresnahan (1981) [3]. This coincidence between the outcomes of a game played by rational players (i.e. the static duopoly game) and irrational players (i.e. the evolutionary game) can be understood intuitively: only those players which maximize their payoff functions taking into consideration the right conjectures about the rival firm’s behavior will be more successful in the market and these conjectures are the ones that remain in an evolutionary game too.
The purpose of this paper is two-fold: First, following the evolutionary duopoly model proposed by Muller and Norman (2005) [9], we derive the ESS for quantity-setting and price-setting oligopolies with conjectural variations, producing heterogeneous goods. We demonstrate that ESS coincides with the Consistent CV in the above oligopoly model. The existing evolutionary studies on CV (referred above) have only shown that the above result holds for duopolies.
Second, we analyze whether the market outcome associated with ESS in the above oligopoly model can be socially optimal. The social optimality of oligopoly market outcomes is an important issue in economic theory and welfare economics. However, not many studies of CV have addressed this issue explicitly. One exception is Jean-Marie and Tidball (2002) [7], who have examined the social optimality of the stable state equilibrium in a learning model4.
We show that the market output and price induced by ESS can be socially optimal only if the firms produce homogeneous products. Moreover, if firms produce heterogeneous goods, the market output under ESS is less than socially optimal (“underproduction”), while the price exceeds the socially optimal price. Interestingly, as the number of firms in the market increases to infinity, the market outcome (output and price) approaches the socially optimal outcome. The above results hold true for quantity competition as well as price competition. The remaining paper is organized as follows:
Section 2 elucidates the general framework and model of our study. In Section 3, we derive the socially optimal outcome of our model, which is used as a benchmark for comparison later on. In Section 4, we derive the Nash equilibrium, Consistent CV and ESS for a quantity game, and obtain conditions for social optimality in the game. Section 5 explains the results of a similar analysis carried out for a price game. We conclude our discussion in Section 6.
2. The Model
We consider an economy populated with a large number of firms which are randomly grouped into n firm oligopolies. Now, let us consider n firms  in a differentiated goods oligopoly market. Inverse demand function for each firm i is linear, given as,
in a differentiated goods oligopoly market. Inverse demand function for each firm i is linear, given as,
 (1)
(1)
where,  (constant),
(constant),  is the price faced by firm
is the price faced by firm ,
,  is the quantity produced by firm
is the quantity produced by firm  and
and  is the aggregate quantity produced by all firms other than firm
is the aggregate quantity produced by all firms other than firm . The parameter
. The parameter  captures the extent of product differentiation in the market, with
captures the extent of product differentiation in the market, with  denoting homogeneous goods and
denoting homogeneous goods and  corresponding to completely differentiated products.
corresponding to completely differentiated products.
Assuming symmetry between  firms other than firm
firms other than firm , (explained in Section 4) i.e.
, (explained in Section 4) i.e.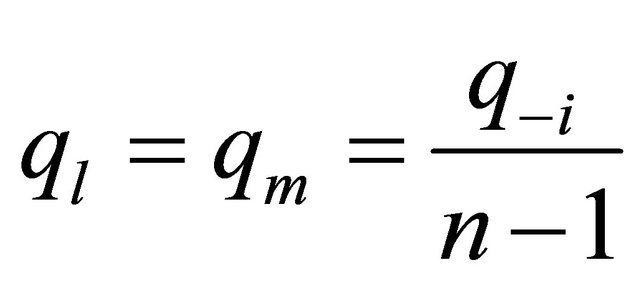 ;
;
 Now, for any firm
Now, for any firm  the inverse demand function can be written as,
the inverse demand function can be written as,
 (2)
(2)
The cost of production for firm  is in quadratic form, written as,
is in quadratic form, written as,
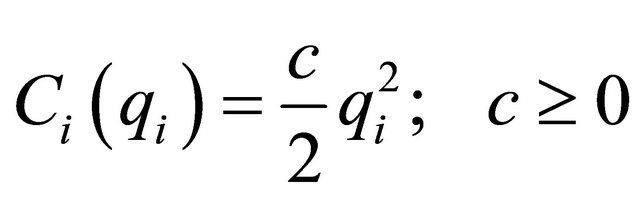 (3)
(3)
If the firm’s decision variable is price, we can change our equations to,
 (4)
(4)
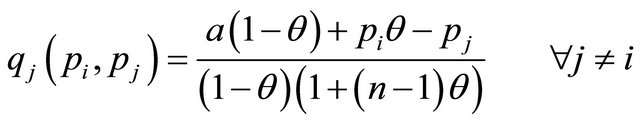 (5)
(5)
Profit functions for either quantity or price competition for firm  can be derived from the equation,
can be derived from the equation,
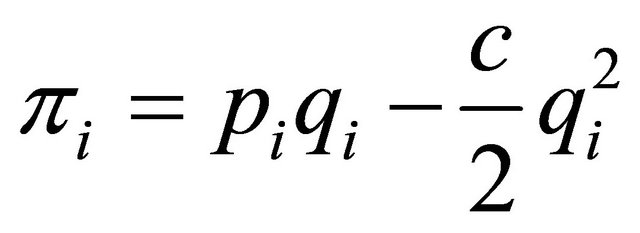 , by substituting the right values.
, by substituting the right values.
3. Socially Optimal Outcome
When each firm in the market acts as a price taker, the total Social Welfare, i.e. the sum of Consumer Surplus and Producer Surplus is maximum with no welfare loss. By equating  (as all n firms face the same demand and cost functions), and summing up, we get the Social Optimal Market output,
(as all n firms face the same demand and cost functions), and summing up, we get the Social Optimal Market output,  and price,
and price, 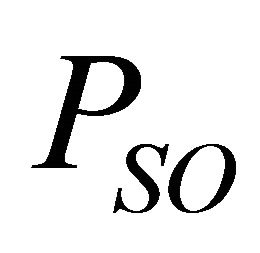 ,
,
 (6)
(6)
In the limit when 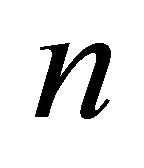 tends to infinity, i.e. as the number of firms increase, we get
tends to infinity, i.e. as the number of firms increase, we get
 (7)
(7)
This is the Monopolistic Competition outcome with a large number of firms (and Perfectly competitive outcome for, ), with zero profits in the market.
), with zero profits in the market.
4. Quantity Competition
4.1. Nash Equilibrium
The first order conditions,  and
and
 where,
where, 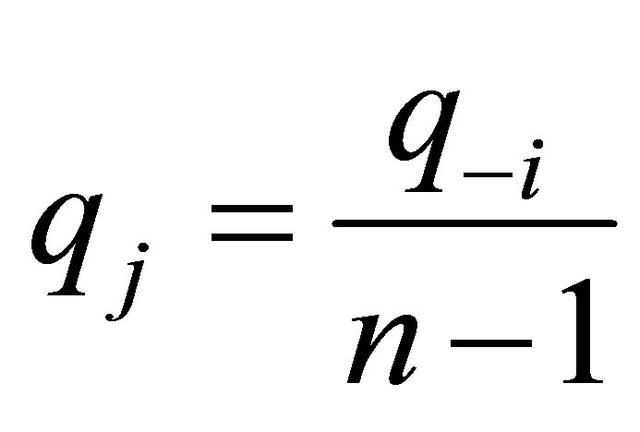 , gives the following reaction function of firm
, gives the following reaction function of firm  and the aggregate reaction function of the rest of the firms,
and the aggregate reaction function of the rest of the firms,
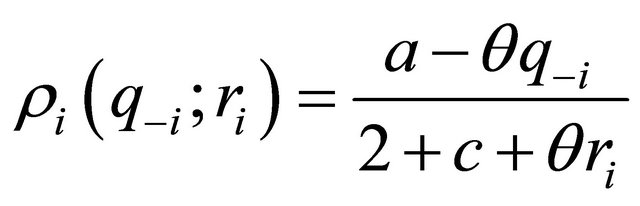 (8)
(8)
 (9)
(9)
where,  ,
,  is the Conjectural Variation (CV)
is the Conjectural Variation (CV)
of firm , i.e. the change expected in the aggregate quantity produced by all other firms in response to a change in its own quantity. The Nash Equilibrium, by solving the above reaction function is,
, i.e. the change expected in the aggregate quantity produced by all other firms in response to a change in its own quantity. The Nash Equilibrium, by solving the above reaction function is,
 (10)
(10)
 (11)
(11)
4.2. Consistent Conjectural Variations (CCV)
We will follow the method adopted by Perry (1982) [12], while trying to solve for the consistent CV assuming complete symmetry between firms. As mentioned in the previous section, we will consider symmetry between  firms. This symmetry assumption is justified as, for consistency, all firms should have the same conjecture about firm
firms. This symmetry assumption is justified as, for consistency, all firms should have the same conjecture about firm , which leads to same conjectures about aggregate output as well.
, which leads to same conjectures about aggregate output as well.
Using Bresnahan’s (1981) definition of consistent CV, where firms correctly guess the reaction of their rival firms while maximizing their profits, we have the CV of a firm equal to the slope of the actual reaction function of the rival firm (here aggregate reaction function).
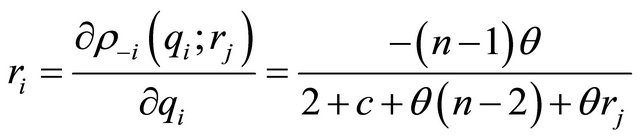 (12)
(12)
Equating , as we are dealing with symmetric consistent conjectures
, as we are dealing with symmetric consistent conjectures , we get,
, we get,
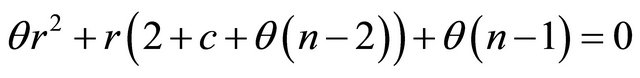 (13)
(13)
The root satisfying the second order condition is,
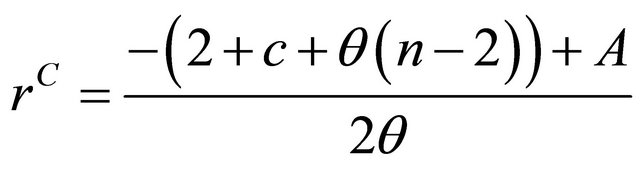 (14)
(14)
where,
 (15)
(15)
4.3. Evolutionarily Stable Strategy (ESS)
Firms can hold any conjectures initially and no rationality condition is imposed on them regarding this decision. However, given their conjectures they play the market game rationally. The evolutionary game then helps in making firms choose conjectures that maximizes their profits in each period (which can be thought of as their reproductive success). The conjectures which lead to a better outcome for a firm will then spread to the whole population. It can also be thought of in another way, the proportion of the firms with good conjectures increase in the population while those with bad conjectures and relatively low evolutionary success fall out of the market. The evolutionary game can be thought of as being played in two steps [9]. First, firms choose their decision variables given their conjectural variations (types) rationally (Nash equilibrium, ). The evolutionary success of firms is given by their profits:
). The evolutionary success of firms is given by their profits:
 (16)
(16)
In the second step each firm maximizes their evolutionary success (profits) by choosing the ESS in the long run. For the same, we will apply the static concept of an ESS (Maynard Smith (1982) [11]).
An equilibrium with ESS conjectures is a set of quantities  and conjecture
and conjecture  such that,
such that,
 (17a)
(17a)
and
 (17b)
(17b)
and
 (17c)
(17c)
The interpretation of the above equations is as follows. The equilibrium with evolutionarily stable conjectures requires the outputs to be the Nash equilibrium (Equation (17a)). The ESS,  is the best response against itself (Equation (17b)). No
is the best response against itself (Equation (17b)). No  -mutant invading a society of
-mutant invading a society of  -players may be more successful than
-players may be more successful than  (Equation (17c)).
(Equation (17c)).
Since the ESS has to be the best response against itself, the evolutionary game will have a symmetric equilibrium, allowing us to continue with the assumption of symmetry between players for ease of calculations.
Substituting Equation (10) in our profit functions gives us the evolutionary success given the firm types in a particular time period, . Firms maximize it with respect to their types (here conjectures) over periods. Since the ESS should be the best response against itself, we replace
. Firms maximize it with respect to their types (here conjectures) over periods. Since the ESS should be the best response against itself, we replace 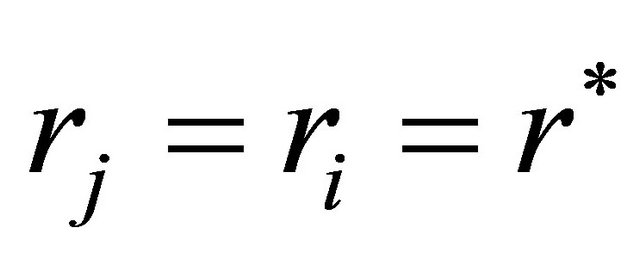 in the first order condition and obtain the following quadratic equation,
in the first order condition and obtain the following quadratic equation,
 (18)
(18)
Note that the above condition is the same as the one derived for Consistency (Equation (13)). Hence, we have the Evolutionarily Stable Conjecture,  ,
,
 (19)
(19)
with  as defined in Equation (15).
as defined in Equation (15).
However for  and
and  (Constant marginal cost and homogeneous goods), the CCV is not evolutionarily stable as it does not satisfy the condition for stability (Equation (17c)).
(Constant marginal cost and homogeneous goods), the CCV is not evolutionarily stable as it does not satisfy the condition for stability (Equation (17c)).
Note that . This means that any increase in quantity by a firm in the market is offset by a decrease in the quantity by the other firms, thereby, decreasing the influence each firm has on the market price. Hence, they are more competitive than the Cournot outcome
. This means that any increase in quantity by a firm in the market is offset by a decrease in the quantity by the other firms, thereby, decreasing the influence each firm has on the market price. Hence, they are more competitive than the Cournot outcome  but less competitive than perfect competition
but less competitive than perfect competition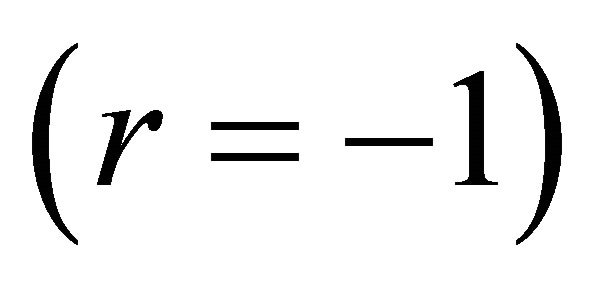 .
.
PROPOSITION 1: The Evolutionarily Stable Strategy for a general n-player quantity game coincides with the Consistent Conjectural Variation.
Now, let us calculate the equilibrium outcome in the evolutionary game. At the ESS, . Substituting them in the Nash Equilibrium (Equation (10)) we find that
. Substituting them in the Nash Equilibrium (Equation (10)) we find that 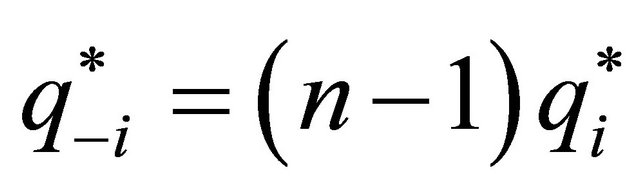 confirming symmetric output by firms in the market. Total market equilibrium output
confirming symmetric output by firms in the market. Total market equilibrium output  and price are calculated to be,
and price are calculated to be,
 (20)
(20)
4.4. Comparing with the Socially Optimal Market Outcome
It can be verified that the ESS equilibrium induces the socially optimal outcome, i.e.
 (21)
(21)
Moreover,
 (22)
(22)
Using (21) and (22), it can be shown that if  = 1 (Homogeneous goods), then
= 1 (Homogeneous goods), then  = 0, and
= 0, and  iff
iff 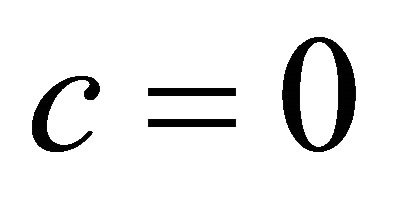 (linear cost), while for
(linear cost), while for 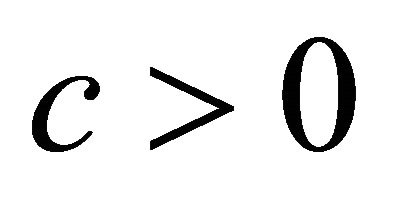 (quadratic cost),
(quadratic cost), .
.
 < 1 (Heterogeneous goods), then
< 1 (Heterogeneous goods), then  < 0, and
< 0, and 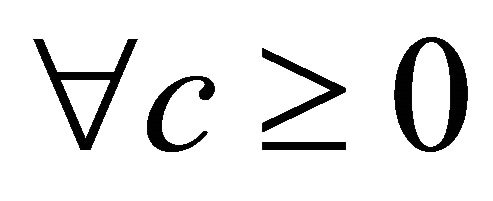 (linear and quadratic cost),
(linear and quadratic cost), .
.
PROPOSITION 2: When firms play with consistent conjectures in a quantity competition oligopoly, only those markets where firms have constant marginal costs and produce homogeneous goods result in a perfectly competitive equilibrium, which is socially optimal. In heterogeneous goods markets, the market output falls short of the socially optimal level of output (“underproduction”).
As the number of firms increase and tend to infinity,
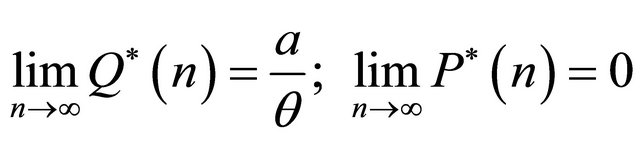 (23)
(23)
Note that the above result coincides with Equation (7), the limit of the Socially Optimal outcome as 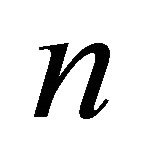 tends to infinity. HencePROPOSITION 3: As the number of firms in the oligopoly increases to infinity, with firms playing an evolutionary game in quantities, the industry outcome approaches the socially optimal market outcome for the given market structure with linear demand and quadratic costs.
tends to infinity. HencePROPOSITION 3: As the number of firms in the oligopoly increases to infinity, with firms playing an evolutionary game in quantities, the industry outcome approaches the socially optimal market outcome for the given market structure with linear demand and quadratic costs.
5. Price Competition
5.1. Nash Equilibrium
In price competition, each firm maximizes its profit with respect to its price. The reaction functions of firms  and
and  are respectively,
are respectively,
 (24)
(24)
 (25)
(25)
where,
 (26)
(26)
 (27)
(27)
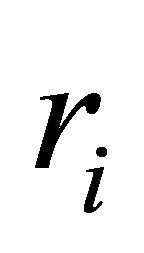 is the conjecture of firm
is the conjecture of firm  about the sum changes in the prices of all other firms due to a change in its own price. Thus,
about the sum changes in the prices of all other firms due to a change in its own price. Thus,
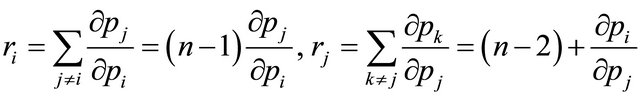 (28)
(28)
Note that as mentioned while describing the model, the symmetry between  firms, which leads to the price of all firms other than firm
firms, which leads to the price of all firms other than firm  be equal i.e.
be equal i.e.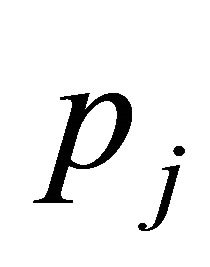 . Now solving for the above two simultaneous equations will give us the Nash Equilibrium,
. Now solving for the above two simultaneous equations will give us the Nash Equilibrium,
 (29)
(29)
in which,
 (30)
(30)
5.2. Consistent Conjectural Variations (CCV)
We will follow the same method as in Section 4.2, of assuming symmetry between firms. Now, for consistency of conjectures in the above price game, we need the conjecture of firm  to be equal to the sum of the slopes of the reaction functions of all other firms,
to be equal to the sum of the slopes of the reaction functions of all other firms,
 (31)
(31)
Replacing the above in terms of  and
and , and letting
, and letting , we get,
, we get,
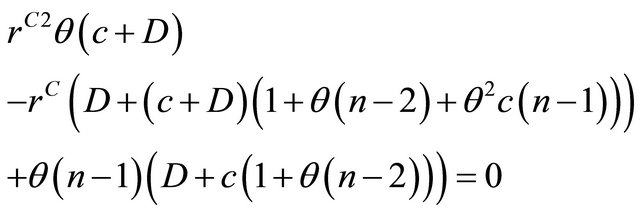 (32)
(32)
The profit maximizing Consistent Conjectural Variation is given by,
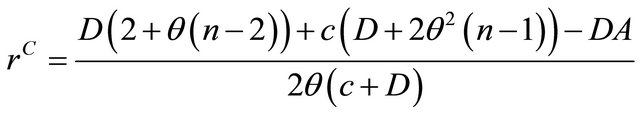 (33)
(33)
with  as defined in Equation (15) and
as defined in Equation (15) and  as defined in Equation (26).
as defined in Equation (26).
5.3. Evolutionarily Stable Strategy (ESS)
The evolutionary success of firms after they play a Nash equilibrium in each period, given by substituting equation (29) in the profit functions, is
 , which the firms maximize with respect to their conjectures, thus evolving to have the stable conjecture. Replacing
, which the firms maximize with respect to their conjectures, thus evolving to have the stable conjecture. Replacing  in the first order condition gives us,
in the first order condition gives us,
 (34)
(34)
Note that the above quadratic (Equation (34)) is same as the quadratic derived for the consistent conjectures (Equation (32)). The Evolutionary Stable Strategy,  for the price competition is given by,
for the price competition is given by,
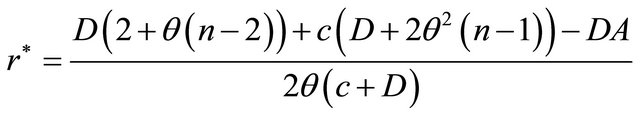 (35)
(35)
with  defined as in Equation (15) and
defined as in Equation (15) and 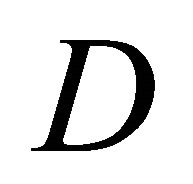 as defined in Equation (26). Also,
as defined in Equation (26). Also,
 (36)
(36)
This means that, a decrease in price of any firm leads to a decrease in the price of the other firms as well, resulting in little possibility of any single firm to be able to capture a large market share by reducing its price. Thus, the outcome is more competitive than Cournot, but less competitive than Bertrand (Perfect Competition), with it being equal to Bertrand at .
.
PROPOSITION 4: The Evolutionarily Stable Strategy for a general n-player Price game coincides with the Consistent Conjectural variation.
Calculating the equilibrium outcome for this game, by substituting for  in the Nash equilibrium gives us,
in the Nash equilibrium gives us,  and
and ,
,
 (37)
(37)
5.4. Comparing with the Socially Optimal Market Outcome
As θ tends to 1 (homogeneous goods), we have,
 (38)
(38)
i.e. the equilibrium gives rise to the Bertrand outcome, which is perfectly competitive.
Also, in general it can be verified that the ESS equilibrium induces the socially optimal outcome, i.e.
 (39)
(39)
Using (39), we have for  (heterogeneous goods),
(heterogeneous goods), . Hence, for all
. Hence, for all  (linear and quadratic cost),
(linear and quadratic cost), .
.
PROPOSITION 5: When firms in the oligopoly with homogeneous goods play an evolutionary game in prices, the market evolves to become perfectly competitive, which leads to the socially optimal outcome. This result holds irrespective of the cost of production of firms and the number of firms in the market. In heterogeneous goods markets, the market price is always greater than the socially optimal price.
When the number of firms in the market increases and tends to infinity,
 (40)
(40)
Note that the above result coincides with Equation (7), the limit of the Social Optimal Output and also Equation (23), the limit of the Quantity Competition Output.
PROPOSITION 6: As the number of firms in the oligopoly increases to infinity, with firms playing an evolutionary game in prices, the industry outcome approaches the socially optimal market outcome for the given market structure with linear demand and quadratic costs.
And finally, it is interesting to note that, as the number of firms in the market increases to infinity, the industry outcome approaches the socially optimal market outcome, regardless of whether the firms are involved in quantity competition or price competition.
6. Conclusions
The evolutionary approach to analyzing Conjectural Variations has revived the idea of the long forgotten Consistent CV, showing us that Consistent CV can be viewed as the ESS of a two-player evolutionary game (duopoly). We have generalized the above result for general n-firm oligopoly markets and have also analyzed the social optimality of ESS in a differentiated goods oligopoly framework, with both quantity competition and price competition. We have demonstrated that the coincidence of Consistent CV and ESS holds for general n-firm oligopolies as well. We have also derived conditions under which the ESS is social optimal.
The above analysis gives us a comprehensive view of how oligopoly markets function. In Cournot’s analysis , extended to a
, extended to a  -firm quantity game, it is well known that the oligopoly market outcome approaches the perfect competitive market outcome as the number of firms increases to infinity. We obtain the same result for oligopoly markets with non-zero conjectures, with both quantity competition and price competition. The above result provides a justification for the use of Consistent CV and shows that the market outcome under Consistent CV (which coincides with ESS) approaches the perfectly competitive outcome as the number of firms increases to infinity.
-firm quantity game, it is well known that the oligopoly market outcome approaches the perfect competitive market outcome as the number of firms increases to infinity. We obtain the same result for oligopoly markets with non-zero conjectures, with both quantity competition and price competition. The above result provides a justification for the use of Consistent CV and shows that the market outcome under Consistent CV (which coincides with ESS) approaches the perfectly competitive outcome as the number of firms increases to infinity.
7. Acknowledgements
An earlier version of the paper was presented at the “International Conference on Game Theory and Operations Research Applications (in honor of Prof. C. R. Rao and Prof. Lloyd Shapley)”, held at Hyderabad, India, during 21-22 December 2012. We thank the conference participants and an anonymous journal referee for their valuable comments and suggestions.
NOTES
2Prior to this, significant research had been carried out on CV in the static framework, where CV is regarded as an “exogenous” variable. A major criticism of this static CV approach is that almost any outcome observed in oligopoly markets can be explained as an equilibrium outcome, with suitable choice of conjectures.
3Two types of strategies are available to firms in a dynamic game: “Open-loop” and “Closed-loop”. The former refers to the set of strategies which are independent of the present state of the system and thus depend only on its initial state. The latter refers to strategies which are designed taking into consideration the information available regarding the system in its present state.
4In their model, the monopoly market outcome is socially optimal. However, while deriving the socially optimal outcome, they only consider the welfare of the agents that are playing the game, i.e. the producers of a good, and ignore the welfare of the consumers, who have an important role in determining the final market outcome.