Comparative Study of the Effect of the Parameters of Sizing Data on Results by the Meshless Methods (MLPG) ()
1. Introduction
Recently Meshless formulations are becoming popular due to their higher adaptivity and lower cost for preparing input data in the numerical analysis. A variety of meshless methods has been proposed so far (Belytschko et al., 1994; Atluri and Shen, 2002; Liu, 2003; Atluri, 2004) [1-6]. Many of them are derived from a weak-form formulation on global domain [1] or a set of local subdomains [4-7].
The meshless local Petrov-Galerkin (MLPG) method originated by Atluri and Zhu [1] uses the so-called local weak form of the Petrov-Galerkin formulation. MLPG has been fine-tuned, improved, and extended by Atluri’s group (Atluri et al., 1999) and other researchers over the years [8-10]. MLPG has been applied to solve elastostatics and elastodynamics problems of solids and plats [11].
The method is a fundamental base for the derivation of many meshless formulations, since trial and test functions are chosen from different functional spaces.
MLPG does not need a global mesh for either function approximation or integration. The procedure is quite similar to numerical methods based on the strong-form formulation, such as the finite difference method (FDM). However, because in the MLPG implementation, moving least squares (MLS) approximation is employed for constructing shape functions, special treatments are needed to enforce the essential boundary conditions [4,7].
The aims of this paper are to study the effect on accuracy and convergence of MLPG methods of different size parameters:  and
and 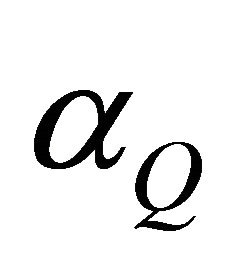 associated to support and quadrature domains respectively. The support domain is denoted be equal to influence domain. For fixed values of:
associated to support and quadrature domains respectively. The support domain is denoted be equal to influence domain. For fixed values of: 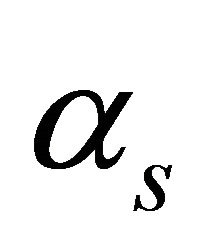 and
and , the effect of cells numbers
, the effect of cells numbers  with nodes distribution number, on energy errors is also studied and some of our results are presented.
with nodes distribution number, on energy errors is also studied and some of our results are presented.
In this work, the MLPG method will be developed for solving the problem of a thin elastic homogenous plate. The discretization and numerical implementation are presented in Section 2 numerical example for 2D problem are given in Section 3. Then paper ends with discussions and conclusions.
2. Basic Equations
Let us consider a two-dimensional problem of solid mechanics in domain  bounded by
bounded by  whose strongform of governing equation and the essential boundary conditions are given by:
whose strongform of governing equation and the essential boundary conditions are given by:
 (1)
(1)
 on
on  (2)
(2)
 on
on  (3)
(3)
where in ,
,  is the stress vector and
is the stress vector and  the body force vector.
the body force vector.
On the natural boundaries  is the prescribed traction,
is the prescribed traction,  denoted the vector of unit outward normal at a point.
denoted the vector of unit outward normal at a point.
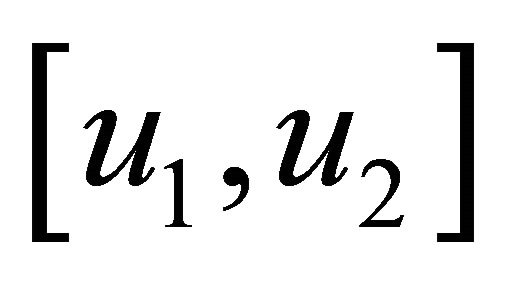 the displacement components in the plan and
the displacement components in the plan and  on the essential boundaries.
on the essential boundaries.
In the local Petrov-Galerkin approaches [3], one may write a weak form over  a local quadrature domain (for node I), which may have an arbitrary shape, and contain the point
a local quadrature domain (for node I), which may have an arbitrary shape, and contain the point  in question, (see Figure 1). The generalized local weak form of the differential Equations (1) and (3) is obtained by:
in question, (see Figure 1). The generalized local weak form of the differential Equations (1) and (3) is obtained by:
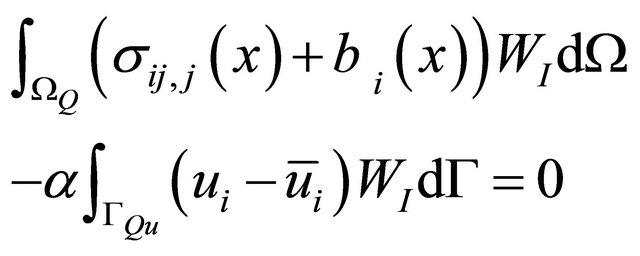 (4)
(4)
where 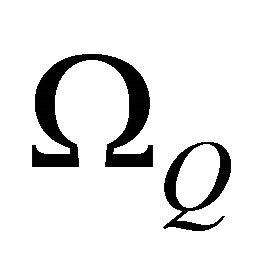 is the local domain of quadrature for node I and
is the local domain of quadrature for node I and  is the part of the essential boundary that intersect with the quadrature domain
is the part of the essential boundary that intersect with the quadrature domain .
. 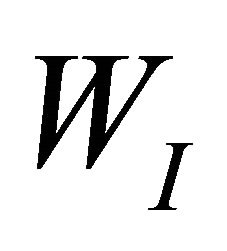 is the weight or test function ,
is the weight or test function , 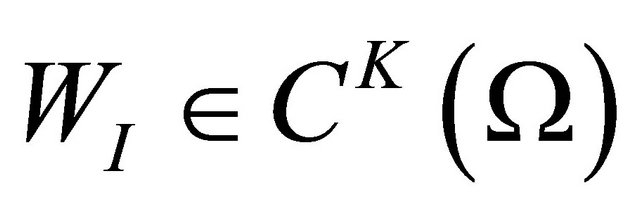 [12]. The first term in Equation (4) is for the equilibrium (in locally weighted average sense) requirement at node I. The second integral in Equation (4) is the curve integral to enforce the essential boundary conditions, because the MLS shape functions used in MLPG lack the Kronecker delta function property.
[12]. The first term in Equation (4) is for the equilibrium (in locally weighted average sense) requirement at node I. The second integral in Equation (4) is the curve integral to enforce the essential boundary conditions, because the MLS shape functions used in MLPG lack the Kronecker delta function property.
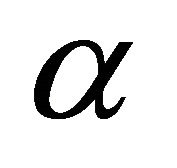 is the penalty factor, Here we use the same penalty factor for all the displacement constraint equations (essential boundary conditions) [1]
is the penalty factor, Here we use the same penalty factor for all the displacement constraint equations (essential boundary conditions) [1]
Generally, in meshfree methods, the representation of field nodes in the domain will be associated to other repartitions of problem domain: influence domain for nodes interpolation,  is the support domain for accuracy. For each node
is the support domain for accuracy. For each node  is the weight function domain, and
is the weight function domain, and  is the quadrature domain for local integration.
is the quadrature domain for local integration.
Using the divergence theorem [11] in Equation (4) we obtain:
 (5)
(5)
where 

Figure 1. The local sub-domains around point  and boundaries.
and boundaries.
 : The internal boundary of the quadrature domain
: The internal boundary of the quadrature domain
 : The part of the natural boundary that intersects with the quadrature domain
: The part of the natural boundary that intersects with the quadrature domain
 : The part of the essential boundary that intersects with the quadrature domain When the quadrature domain
: The part of the essential boundary that intersects with the quadrature domain When the quadrature domain  is located entirely within the global domain on
is located entirely within the global domain on 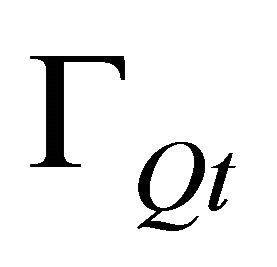 and
and  no boundary conditions are specified then
no boundary conditions are specified then .
.
Unlike the Galerkin method, the Petrov-Galerkin method chooses the trial and test functions from different spaces. The weight function  is purposely selected in such a way that it vanishes on
is purposely selected in such a way that it vanishes on . We can then change the expression of Equation (5):
. We can then change the expression of Equation (5):
 (6)
(6)
Witch is the local Petrov-Galerkin weak form. Here we require  [3,11] and the simplified Petrov-Galerkin form is:
[3,11] and the simplified Petrov-Galerkin form is:
 (7)
(7)
Precedent equations are used to establish the discrete equations for all the nodes whose quadrature domain falls entirely within the problem domain (Equation (7)) and to establish the discrete equations for all the boundary nodes or the nodes whose quadrature domain intersects with the problem boundary “Equation (6)”.
To approximate the distribution of the function  in
in  the support domain over a number of nodes
the support domain over a number of nodes . We shall have the approximant
. We shall have the approximant  of
of  [13]
[13]
 (8)
(8)
where I denote the set of the nodes in the support domain  of point
of point .
.
 the MLS shape function for node I that is created using nodes in the support domain
the MLS shape function for node I that is created using nodes in the support domain  of point
of point . The discrete system in Equation (6) is given in matrix form:
. The discrete system in Equation (6) is given in matrix form:
 (9)
(9)
where  is a matrix that collects the derivatives of the weight functions in Equation (6), and
is a matrix that collects the derivatives of the weight functions in Equation (6), and
 is the matrix of weight function. The stress vector defined by:
is the matrix of weight function. The stress vector defined by:
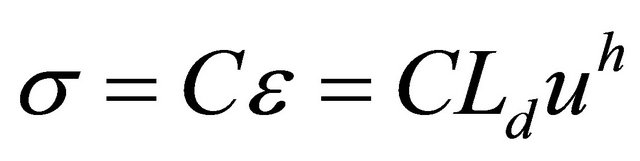 (10)
(10)
where  is the symmetric elasticity tensor of the material
is the symmetric elasticity tensor of the material

Substituting the differential operator
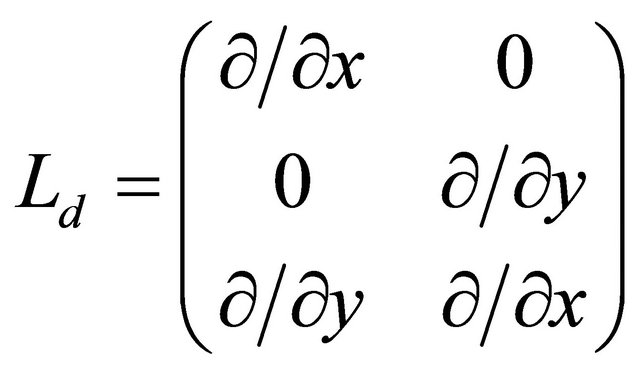 and Equation (8) into Equation (10) we obtain:
and Equation (8) into Equation (10) we obtain:
 (11)
(11)
where 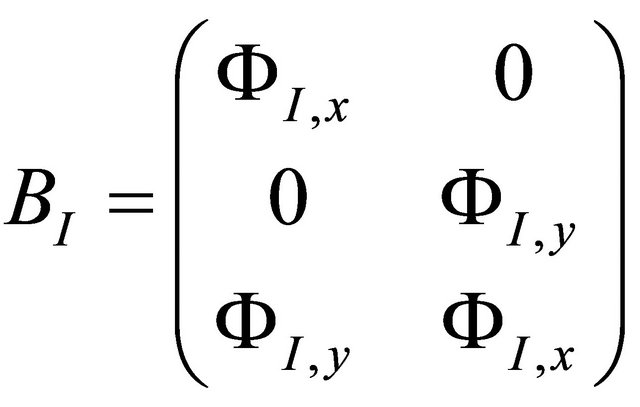 and by using
and by using 
the tractions of a point x can be written as:
 (12)
(12)
Substituting Equations (8), (11) and (12) into Equation (6), we obtain the discrete systems of linear equations for the node I.
 (13)
(13)
That can assembled in matrix form:
 (14)
(14)
where nodal stiffness matrix
 (15)
(15)
And nodal force vector with contributions from body forces applied in the problem domain, tractions applied on the natural boundary, as well as the penalty force terms.
 (16)
(16)
Two independent linear equations can be obtained for each node in the entire problem domain and assembled all these  equations to obtain the final global system equations:
equations to obtain the final global system equations:
 (17)
(17)
To solve the precedent system, the standard Gauss quadrature formula is applied with 16 Gauss points [3,14] for evaluation of boundary and domain integrals in Equations (15) and (16)
3. Numerical Example
In this section, numerical results are presented for Cantilever rectangular plate in Figure 2. First we investigate the effects of the size of support or quadrature domains and we examine the numerically convergence of MLPG, then comparisons will be made with the analytic solution [15]
The problem data:
The height of the beam  and the length of the beam:
and the length of the beam: 
The thickness of the plat:  and Loading (integration of the distributed traction):
and Loading (integration of the distributed traction): 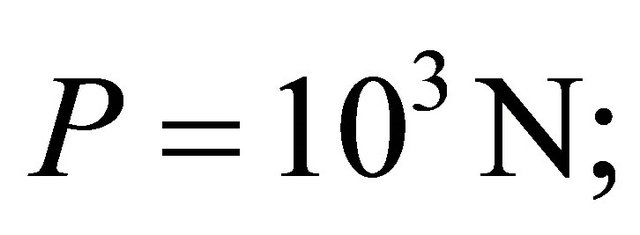
Young’s modulus:  and Poisson’s ratio:
and Poisson’s ratio: 
The standard Gaussian quadrature formula is applied with 16 Gauss points, and for MLS approximation linear polynomial basis functions are applied, the cubic spline function is used as the test function for the local Petrov-
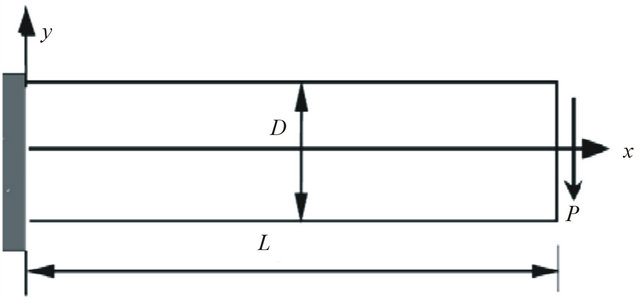
Figure 2. Cantilever plate subjected to distributed traction at the free end.

Figure 3. 55 regular field nodes on the problem domain and boundaries.
Galerkin weak-form. In our numerical calculations we consider many regular distributions of nodes: 55 or 175. To calculate the error energy a background cells is required, then we have varying the number of cell. To obtain the distribution of the deflection and stress through the plates, size of quadrature domain and support domain are varied. Nodal configuration for a cantilever plate with 55 nodes (Figure 3) (nodal distance ) and the sizes of
) and the sizes of  is defined by:
is defined by: 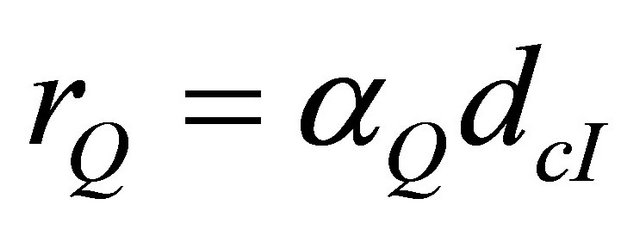 where
where  is the nodal spacing near node I and
is the nodal spacing near node I and  is the size of the local quadrature domain for node I. The sizes of quadrature domains will be, there fore determined by
is the size of the local quadrature domain for node I. The sizes of quadrature domains will be, there fore determined by  and
and  which are dimensionless coefficients in x and y directions, respectively. For simplicity
which are dimensionless coefficients in x and y directions, respectively. For simplicity  is used. The dimension of the support domain is determined by
is used. The dimension of the support domain is determined by  and
and  is the dimensionless size of support domain.
is the dimensionless size of support domain.
4. Discussions
Figure 4 Shows the variation of the effective transverse shear stress 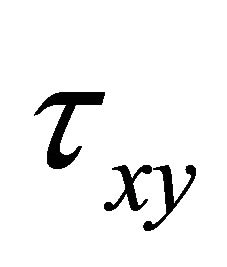 at different points on vertical of the plate by varying
at different points on vertical of the plate by varying for
for  and
and . It can be seen the shear stress distributions on the cross-section at in other sections (
. It can be seen the shear stress distributions on the cross-section at in other sections (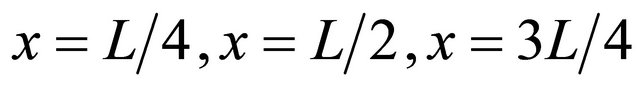 and
and ). it’s shown that the shape is identical to that obtained by theoretical analysis ( section
). it’s shown that the shape is identical to that obtained by theoretical analysis ( section ).
).
The accuracy is clear for the greater value of field nodes distribution. It is also shown in this figure, on the cross-section the meshless MLPG agree well with those from analytical solution (dashed lines).
Figure 5 displays the variation of the energy error as a function of the size of the local support domain, for fixed value of , a background cells is needed, we take
, a background cells is needed, we take . We note on the figure the effect distribution field nodes number on the result, we take n = 55 and 175 number of cell is
. We note on the figure the effect distribution field nodes number on the result, we take n = 55 and 175 number of cell is  and 144 respectively.
and 144 respectively.