Free-Form Laminated Doubly-Curved Shells and Panels of Revolution Resting on Winkler-Pasternak Elastic Foundations: A 2-D GDQ Solution for Static and Free Vibration Analysis ()
1. Introduction
During the last sixty years, two-dimensional linear theories of thin shells have been developed including important contributions by Timoshenko and Woinowsky-Krieger [1], Flügge [2], Gol’denveizer [3], Novozhilov [4], Vlasov [5], Ambartusumyan [6], Kraus [7], Leissa [8,9], Markuš [10], Ventsel and Krauthammer [11] and Soedel [12]. All these contributions are based on the KirchhoffLove assumptions. The transverse shear deformation has been incorporated into shell theories by following the theory of Reissner-Mindlin [13], also named First-order Shear Deformation Theory (FSDT). Abandoning the assumption related to the preservation of the normals to the shell middle surface after the deformation, a comprehensive analysis for elastic isotropic shells was made by Kraus [7], Gould [14,15] and Qatu [16,17]. The present work is just based on the FSDT. In order to include the effect of the initial curvature in the evaluation of the stress resultants a generalization of the Reissner-Mindlin (RM) theory has been proposed in literature by Kraus [7], Qatu [16,17] and Toorani and Lakis [18,19]. There are three different ways to evaluate the engineering elastic constants in the study of curved shells. The first is the Reissner-Mindlin approach [7] that consists in neglecting the effect of curvatures. Using this approach the engineering elastic stiffnesses are constant and do not depend on curvatures. The second one, proposed by Kraus [7] and Toorani and Lakis [18], is based on the Taylor expansion, while the third one proposed by Qatu [16] consists in the exact integration of the elastic constants. As a consequence of the use of these considerations, the stress resultants directly depend on the geometry of the structure in terms of the curvature coefficients. In this latter case, the hypothesis of the symmetry of the in-plane shearing force resultants and the torsional couples declines. A further improvement of the previous theories of shells has been proposed by Toorani and Lakis [19]. In the present work their kinematic model is used in order to include the effect of the curvature from the beginning of the shell formulation. In this way, the strain relationships have to change and, as a consequence, the equilibrium equations in terms of displacements have to be modified. In the present paper, the proposed shell theory, named General Shell Theory (GST), is considered and compared with the Reissner-Mindlin (RM) theory. Comparisons between these two different formulations are presented in this paper. Several studies dealing with the shells theory have been presented years before. The most popular numerical tool used to perform the static and dynamic analyses is currently the finite element method [14,15,20]. The generalized collocation method based on the ring element method has also been applied. In this method, each static and kinematic variable is transformed into a theoretically infinite Fourier series of harmonic components, with respect to the circumferential co-ordinate [21,22]. In other words, when dealing with a completely closed shell, the 2D problem can be reduced using standard Fourier decomposition. For a panel, however, it is not possible to perform such a reduction operation, and the two dimensional field must be directly dealt, as it will just be done in the present work. Furthermore, the system of second-order linear partial differential equations is solved, without resorting to the one-dimensional formulation of the equilibrium of the shell. Complete revolution shells are obtained as special cases of shell panels by satisfying the kinematical and physical compatibility at the common meridian with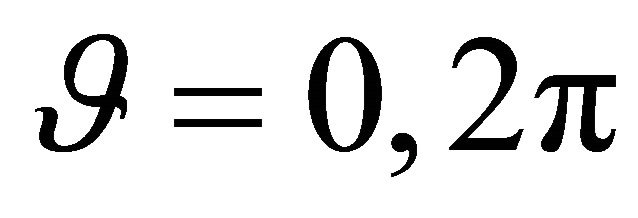 . The excellent mathematical and computational algorithmic properties, combined with successful industrial applications, have contributed to the enormous popularity of the Rational Bézier and Non-Uniform Rational B-Splines (NURBS) curves [23-25]. These curves allow to generalize the shape of the shell meridian and can be used for the optimization of the structure itself. By introducing the Differential Quadrature rule [26] and the simple mathematical formulation of the Rational Bézier and NURBS curves [23-25], it is possible to numerically evaluate the geometric parameters of a free-form shell of revolution. For the sake of simplicity and without loosing generality, only Rational Bézier curves are used in this study. Due to the increasing importance of the interaction of shells with the elastic medium, the Winkler-Pasternak foundation is introduced. Differently from papers presented in literature [27-31], all the effects of the foundation, except the damping, are separately considered. New results are presented in order to investigate the effects of the Winkler modulus, the Pasternak modulus and the inertia of the elastic foundation on the behavior of laminated shells of revolution. The mathematical fundamentals and recent developments of the GDQ method as well as its major applications in engineering are discussed in detail in the book by Shu [26]. The interest of researches in this procedure is increasing due to its great simplicity and versatility. As shown in the literature [32], GDQ technique is a global method which can obtain very accurate numerical results by using a considerably small number of grid points. Therefore, this simple direct procedure has been applied in a large number of cases [33- 85] to circumvent the difficulties of programming complex algorithms for the computer, as well as to reduce the computational time. In conclusion, the aim of the present paper is to demonstrate an efficient and accurate application of the Differential Quadrature approach, by solving the equations governing the static and the free vibration of laminated composite doubly-curved moderately thick shells and panels of revolution. Summarizing, this research deals with four aspects. The first is the improvement of the Reissner-Mindlin Theory using a different kinematical model. In this way the effect of the curvature of the shell structure is considered from the beginning of the theory derivation. The second is the generalization of the shape of the shell meridian. The Differential Quadrature rule is used to evaluate the geometric parameters needed to describe the geometry of the structure when a Rational Bézier meridian curve is assumed. The third is the investigation of the effects of Winkler-Pasternak foundations on the behavior of the shell structures in static and dynamic analyses. All the effects of the foundation are separately considered. The fourth is the use of the Generalized Differential Quadrature method to solve the governing shell equations.
. The excellent mathematical and computational algorithmic properties, combined with successful industrial applications, have contributed to the enormous popularity of the Rational Bézier and Non-Uniform Rational B-Splines (NURBS) curves [23-25]. These curves allow to generalize the shape of the shell meridian and can be used for the optimization of the structure itself. By introducing the Differential Quadrature rule [26] and the simple mathematical formulation of the Rational Bézier and NURBS curves [23-25], it is possible to numerically evaluate the geometric parameters of a free-form shell of revolution. For the sake of simplicity and without loosing generality, only Rational Bézier curves are used in this study. Due to the increasing importance of the interaction of shells with the elastic medium, the Winkler-Pasternak foundation is introduced. Differently from papers presented in literature [27-31], all the effects of the foundation, except the damping, are separately considered. New results are presented in order to investigate the effects of the Winkler modulus, the Pasternak modulus and the inertia of the elastic foundation on the behavior of laminated shells of revolution. The mathematical fundamentals and recent developments of the GDQ method as well as its major applications in engineering are discussed in detail in the book by Shu [26]. The interest of researches in this procedure is increasing due to its great simplicity and versatility. As shown in the literature [32], GDQ technique is a global method which can obtain very accurate numerical results by using a considerably small number of grid points. Therefore, this simple direct procedure has been applied in a large number of cases [33- 85] to circumvent the difficulties of programming complex algorithms for the computer, as well as to reduce the computational time. In conclusion, the aim of the present paper is to demonstrate an efficient and accurate application of the Differential Quadrature approach, by solving the equations governing the static and the free vibration of laminated composite doubly-curved moderately thick shells and panels of revolution. Summarizing, this research deals with four aspects. The first is the improvement of the Reissner-Mindlin Theory using a different kinematical model. In this way the effect of the curvature of the shell structure is considered from the beginning of the theory derivation. The second is the generalization of the shape of the shell meridian. The Differential Quadrature rule is used to evaluate the geometric parameters needed to describe the geometry of the structure when a Rational Bézier meridian curve is assumed. The third is the investigation of the effects of Winkler-Pasternak foundations on the behavior of the shell structures in static and dynamic analyses. All the effects of the foundation are separately considered. The fourth is the use of the Generalized Differential Quadrature method to solve the governing shell equations.
2. Shell Fundamental Equations
The basic configuration of the problem herein considered is a laminated composite doubly-curved shell [83] as shown in Figure 1. The co-ordinates along the meridian and circumferential directions of the reference surface are  and
and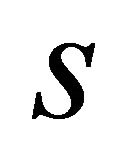 , respectively. The distance of each point from the shell mid-surface along the normal is
, respectively. The distance of each point from the shell mid-surface along the normal is . It is considered a laminated composite shell made of
. It is considered a laminated composite shell made of  laminae or plies, where the total thickness of the shell
laminae or plies, where the total thickness of the shell  is defined as:
is defined as:
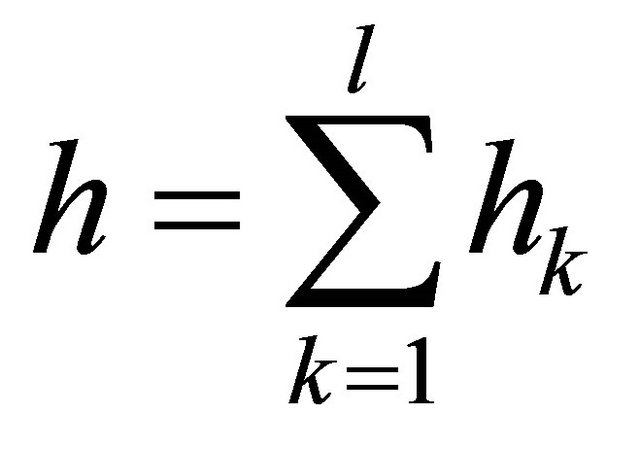 (1)
(1)
in which 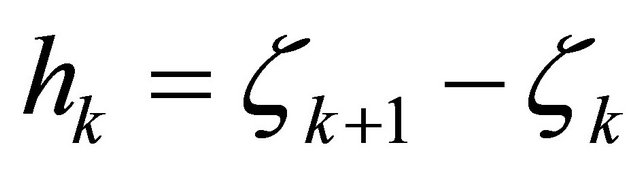 is the thickness of the k-th lamina or ply. In this work, doubly-curved shells of revolution are considered. For this type of structures the analytical expressions of the meridian curve are reported in the work by Tornabene [78], so that no further considerations will be introduced. The angle formed by the extended normal n to the reference surface and the axis of rotation
is the thickness of the k-th lamina or ply. In this work, doubly-curved shells of revolution are considered. For this type of structures the analytical expressions of the meridian curve are reported in the work by Tornabene [78], so that no further considerations will be introduced. The angle formed by the extended normal n to the reference surface and the axis of rotation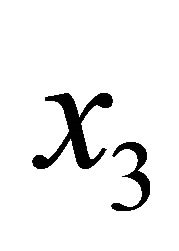 , or the geometric axis
, or the geometric axis 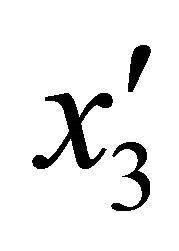 of the meridian curve, is defined as the meridian angle
of the meridian curve, is defined as the meridian angle ; the angle between the radius of the parallel circle
; the angle between the radius of the parallel circle 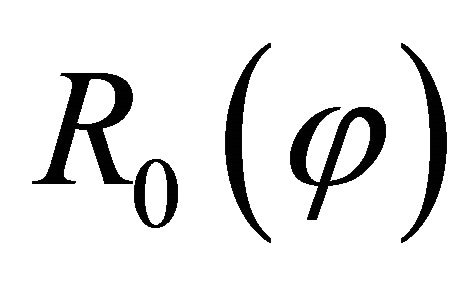 and the
and the 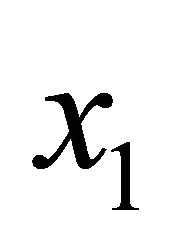 axis is designated as the circumferential angle
axis is designated as the circumferential angle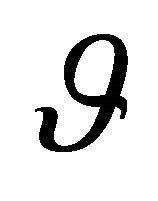 , as shown in Figure 2.
, as shown in Figure 2.
For these structures the parametric co-ordinates 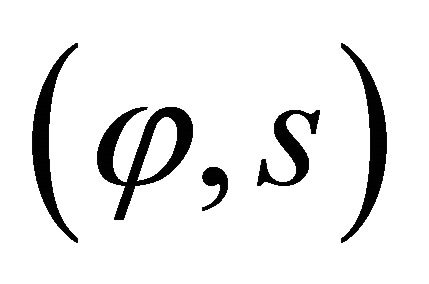 define, respectively, the meridian curves and the parallel circles upon the middle surface of the shell. The curvilinear abscissa
define, respectively, the meridian curves and the parallel circles upon the middle surface of the shell. The curvilinear abscissa 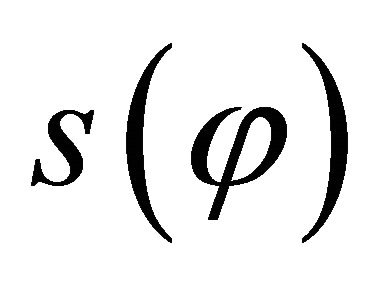 of a generic parallel is related to the circumferential angle
of a generic parallel is related to the circumferential angle  by the relation
by the relation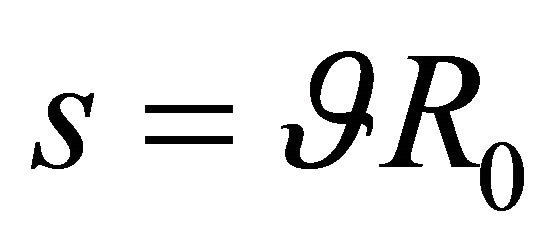 . The horizontal radius
. The horizontal radius 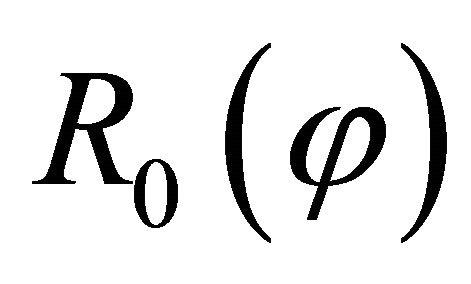 of a generic parallel of the shell represents the distance of each point from the axis of revolution
of a generic parallel of the shell represents the distance of each point from the axis of revolution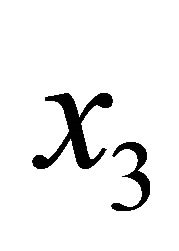 .
. 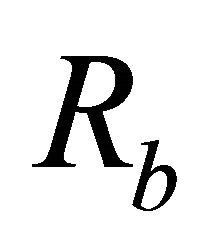 is the shift of the geometric axis of the curved meridian
is the shift of the geometric axis of the curved meridian 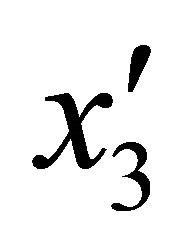 with reference to the axis of revolution
with reference to the axis of revolution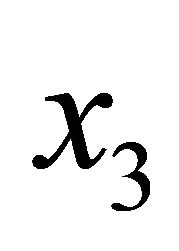 . The position of an arbitrary point within the shell material is defined by co-ordinates
. The position of an arbitrary point within the shell material is defined by co-ordinates 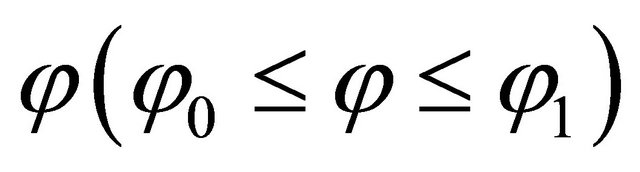 ,
, 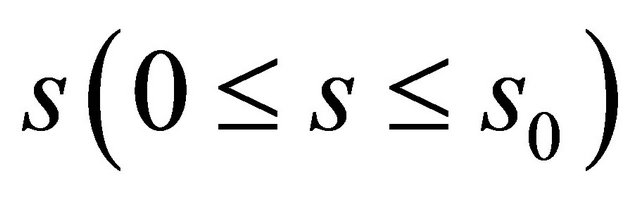 upon the middle surface, and
upon the middle surface, and  directed along the outward normal and measured from the reference surface
directed along the outward normal and measured from the reference surface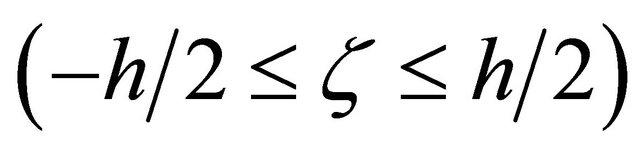 . The geometry of shells considered [83] is a surface of revolution (Figure 2).
. The geometry of shells considered [83] is a surface of revolution (Figure 2).
A simple way to define a general meridian curve is to use the well-known Rational Bézier representation of a plane curve [24,25,80]. In particular, it is possible to describe a Rational Bézier curve in the following manner:
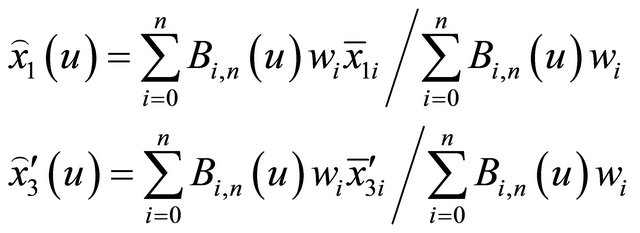 (2)
(2)
where 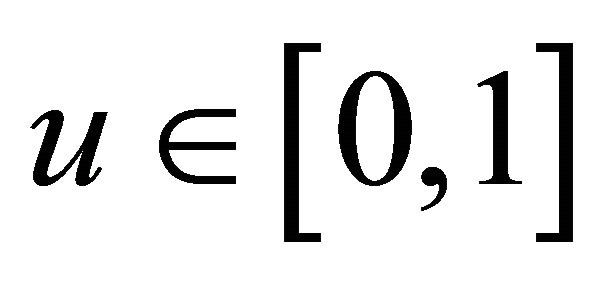 is the curve parameter,
is the curve parameter, 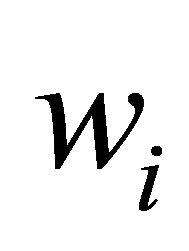 are the weight coefficients and
are the weight coefficients and 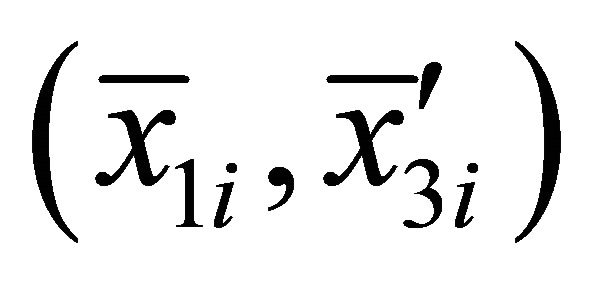 are the co-ordinates of the curve control points. Furthermore, the classical n-th degree Bernstein polynomial formulations are given by:
are the co-ordinates of the curve control points. Furthermore, the classical n-th degree Bernstein polynomial formulations are given by:

Figure 1. Co-ordinate system of a laminated composite doubly-curved shell.

Figure 2. Shell geometry: Meridian section (a); Circumferential section (b).
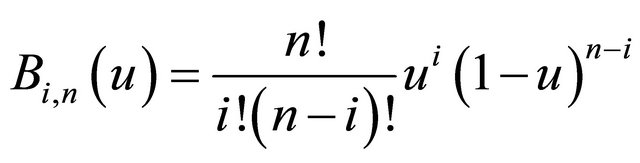 (3)
(3)
In this way, only the co-ordinates of the curve 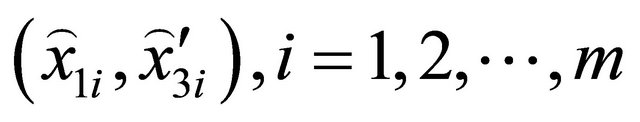 , are known in the co-ordinate reference system
, are known in the co-ordinate reference system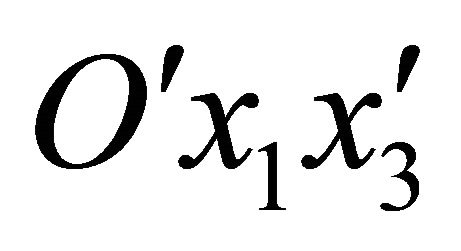 . In order to solve the shell problem, it is important to express the horizontal radius
. In order to solve the shell problem, it is important to express the horizontal radius 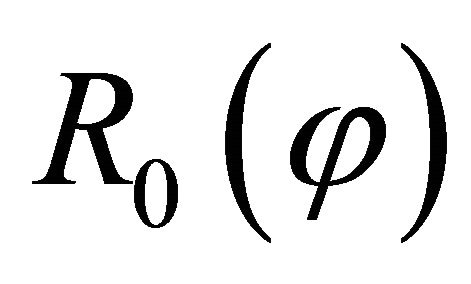 of a generic parallel and the radii of curvature
of a generic parallel and the radii of curvature 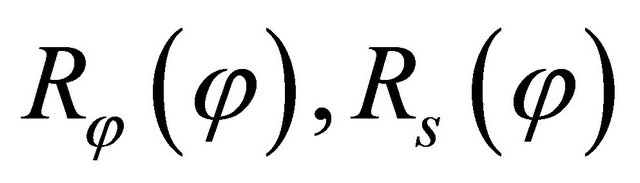 in the meridian and circumferential directions as functions of
in the meridian and circumferential directions as functions of . Based on the differential geometry [7,12,57,80,83], the radius of curvature of the meridian curve can be described as a function of
. Based on the differential geometry [7,12,57,80,83], the radius of curvature of the meridian curve can be described as a function of 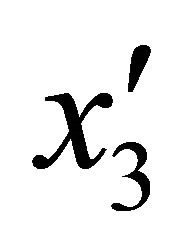 using the following expression:
using the following expression:
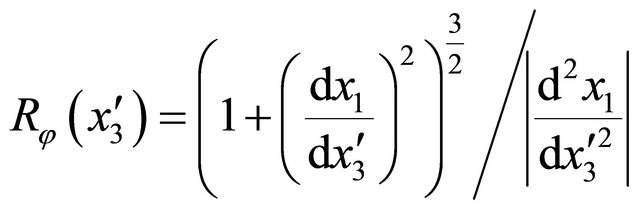 (4)
(4)
It is worth noting that the derivatives of the meridian curve are not known a priori, so that a numeric method to evaluate the first and second derivatives of the meridian curve is required. The differential quadrature rule allows to approximate these derivatives using the following definition [26]:
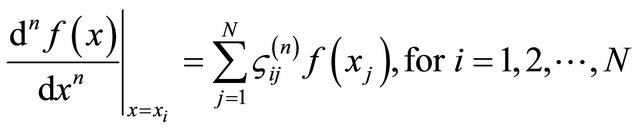 (5)
(5)
where 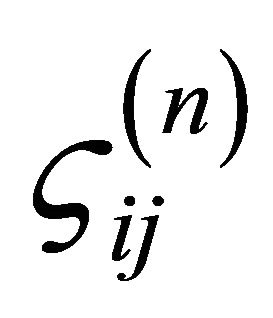 are the weighting coefficients of the n-th order derivative. By discretizing the domain
are the weighting coefficients of the n-th order derivative. By discretizing the domain

using the Chebyshev-Gauss-Lobatto (C-G-L) grid distribution:
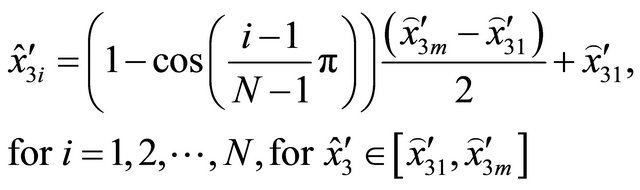 (6)
(6)
and interpolating the 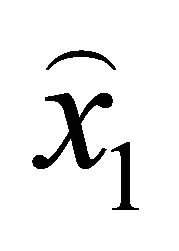 co-ordinates of the curve points derived by the Equations (2) using the previous calculated points (6), the general curve can be represented by the new co-ordinates points
co-ordinates of the curve points derived by the Equations (2) using the previous calculated points (6), the general curve can be represented by the new co-ordinates points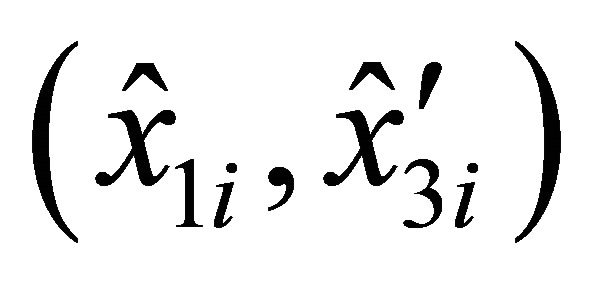 , for
, for . Applying the differential quadrature definition (5), the expression (4) assumes the following discrete aspect:
. Applying the differential quadrature definition (5), the expression (4) assumes the following discrete aspect:
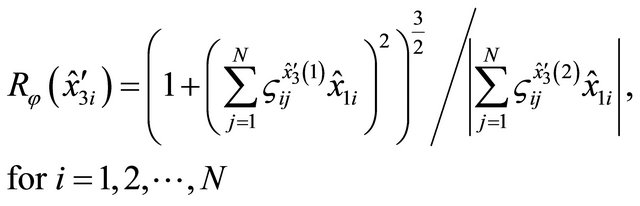 (6)
(6)
where 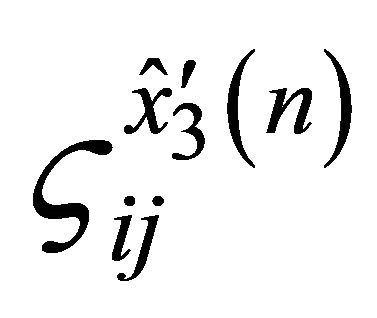 are the weighting coefficients evaluated in the domain
are the weighting coefficients evaluated in the domain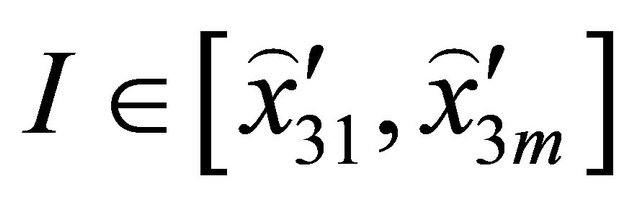 . As a results of the differential geometry [7,12,57,80,83], it is possible to introduce the following relation:
. As a results of the differential geometry [7,12,57,80,83], it is possible to introduce the following relation:
 (7)
(7)
By using the differential quadrature definition (5), the relation (7) can be expressed in the discrete form:
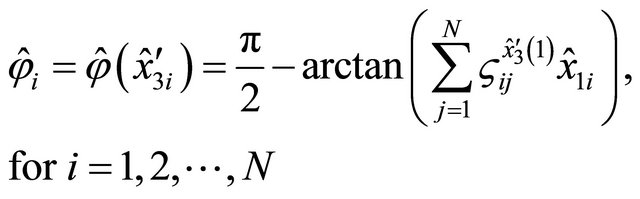 (8)
(8)
By discretizing the domain 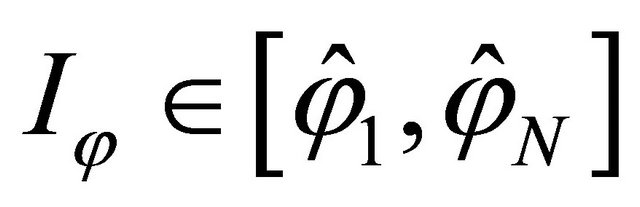 using the Chebyshev-Gauss-Lobatto (C-G-L) grid distribution:
using the Chebyshev-Gauss-Lobatto (C-G-L) grid distribution:
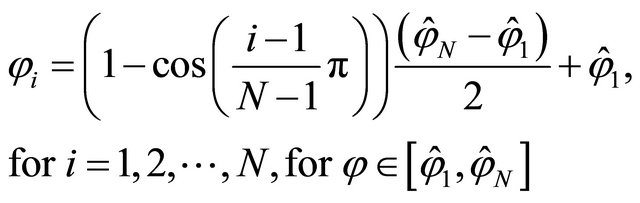 (9)
(9)
and interpolating the  and
and  co-ordinates of the curve points using the calculated points (9), the general curve can be represented by the following new co-ordinate points
co-ordinates of the curve points using the calculated points (9), the general curve can be represented by the following new co-ordinate points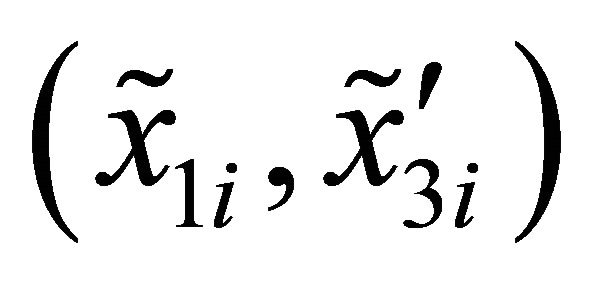 , for
, for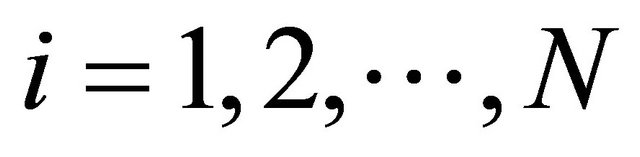 . Thus, all the discrete points of the curve are determined in terms of the co-ordinates
. Thus, all the discrete points of the curve are determined in terms of the co-ordinates  and the angle
and the angle . In the Figure 3, a Rational Bézier curve, its control points and the curve co-ordinates
. In the Figure 3, a Rational Bézier curve, its control points and the curve co-ordinates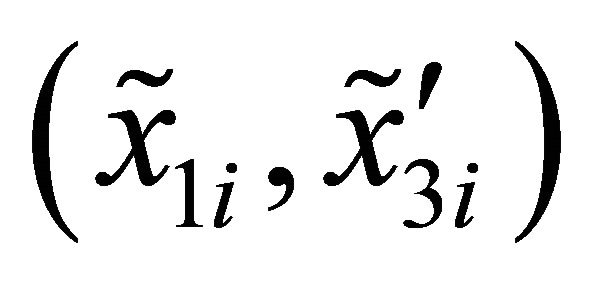 , evaluated as above exposed, are represented [80]. The vectors of the control points and the weights used in Figure 3 are the following:
, evaluated as above exposed, are represented [80]. The vectors of the control points and the weights used in Figure 3 are the following:
 (10)
(10)
Based on the previous considerations, the horizontal radius 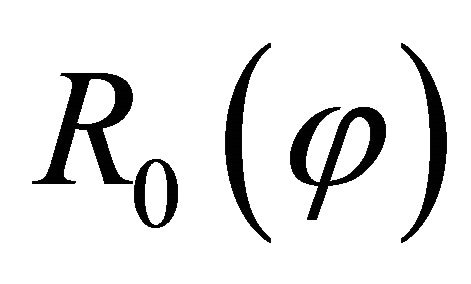 of a shell of revolution assumes the following discrete form:
of a shell of revolution assumes the following discrete form:
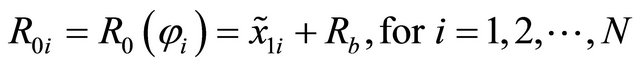 (11)
(11)
For doubly-curved revolution shells the Gauss-Codazzi relation can be expressed as follows:
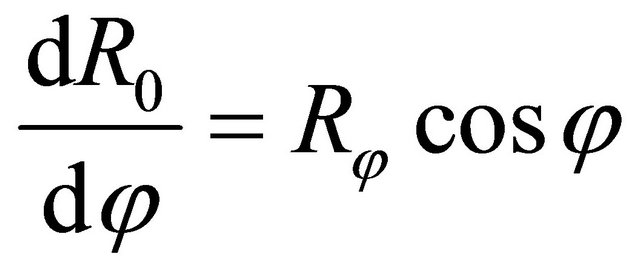 (12)
(12)
By using the differential quadrature definition (5), it is possible to determine the radius of curvature 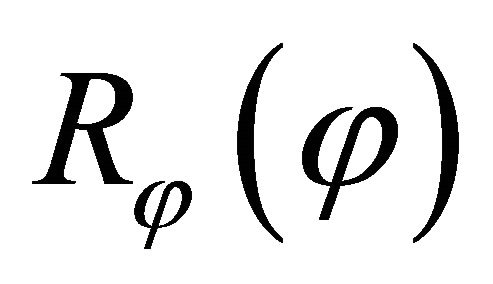 in meridian direction and its first and second derivatives in discrete form:
in meridian direction and its first and second derivatives in discrete form:
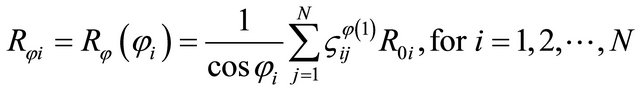 (13)
(13)
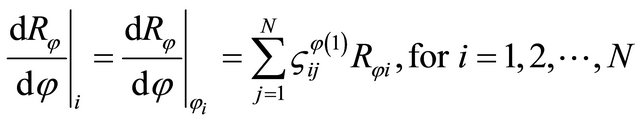 (14)
(14)
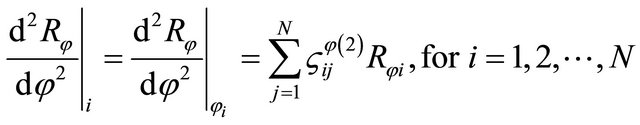 (15)
(15)
Finally, as a results of the differential geometry [7,12, 57,80,83], the radius of curvature 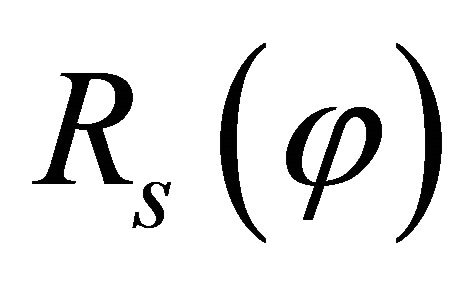 in circumferential direction for a shell of revolution can be expressed in a discrete form as follows:
in circumferential direction for a shell of revolution can be expressed in a discrete form as follows:
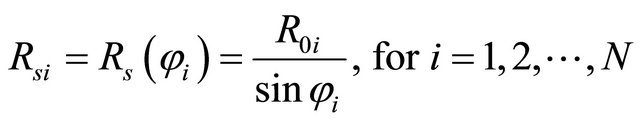 (16)
(16)
It is worth noting that, following the previous considerations, all the useful geometric parameters describing the surface of revolution under consideration are known in discrete form (11)-(16). As shown, the differential quadrature rule (5) has been used to approximate the derivatives needed for the definition of the geometry of a shell of revolution. As concerns the shell theory, the present work is based on the following assumptions: 1) the transverse normal is inextensible so that the normal strain is equal to zero: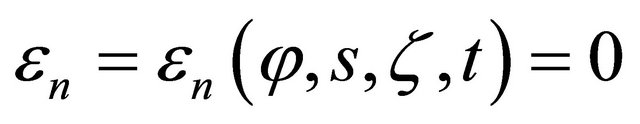 ; 2) the transverse shear deformation is considered to influence the governing equations so that normal lines to the reference surface of the shell before deformation remain straight, but not necessarily normal after deformation (a relaxed KirchhoffLove hypothesis); 3) the shell deflections are small and the strains are infinitesimal; 4) the shell is moderately thick, therefore it is possible to assume that the thickness direction normal stress is negligible so that the in-plane assumption can be invoked:
; 2) the transverse shear deformation is considered to influence the governing equations so that normal lines to the reference surface of the shell before deformation remain straight, but not necessarily normal after deformation (a relaxed KirchhoffLove hypothesis); 3) the shell deflections are small and the strains are infinitesimal; 4) the shell is moderately thick, therefore it is possible to assume that the thickness direction normal stress is negligible so that the in-plane assumption can be invoked: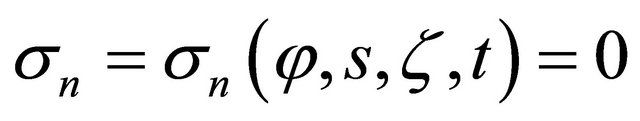 ; 5) the linear elastic behavior of anisotropic materials is assumed; 6) the rotary inertia and the initial curvature are also taken into account. Consistent with the assumptions of a moderately thick shell theory reported above, the displacement field considered in this study follows the First-order Shear Deformation Theory and it can be put in the following form:
; 5) the linear elastic behavior of anisotropic materials is assumed; 6) the rotary inertia and the initial curvature are also taken into account. Consistent with the assumptions of a moderately thick shell theory reported above, the displacement field considered in this study follows the First-order Shear Deformation Theory and it can be put in the following form:
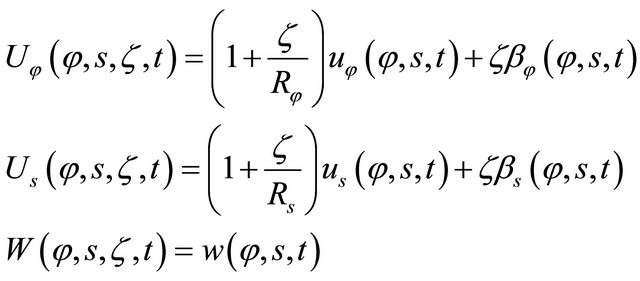 (17)
(17)
where 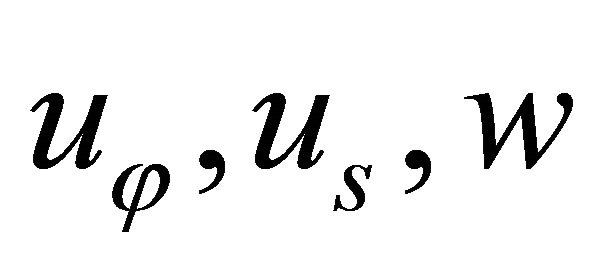 are the displacement components of points lying on the middle surface
are the displacement components of points lying on the middle surface  of the shell, along meridian, circumferential and normal directions, respectively, while
of the shell, along meridian, circumferential and normal directions, respectively, while  is the time variable.
is the time variable. 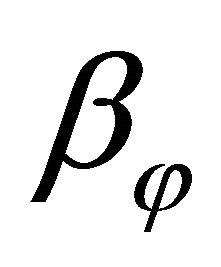 and
and 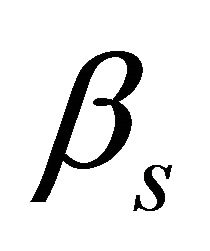 are normal-to-mid-surface rotations, respectively. The kinematic hypothesis expressed by Equations (17) should be supplemented by the statement that the shell deflections are small and strains are infinitesimal, that is
are normal-to-mid-surface rotations, respectively. The kinematic hypothesis expressed by Equations (17) should be supplemented by the statement that the shell deflections are small and strains are infinitesimal, that is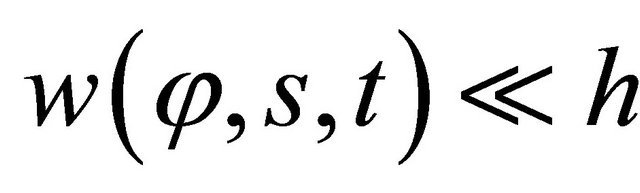 . The in-plane displacements
. The in-plane displacements 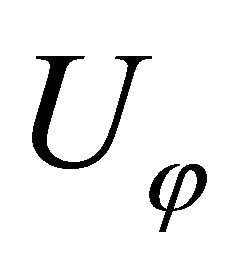 and
and 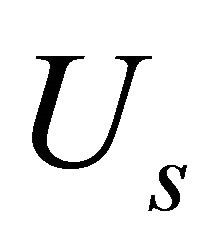 vary linearly through the thickness, while
vary linearly through the thickness, while 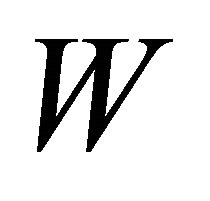 remains independent of
remains independent of . It should be also remarked that, differently from the previous works by Tornabene [65,77,78], the displacement field has been improved taking into account the real geometry of the shell and in particular the curvature effect has been directly introduced into the kinematical model as proposed by Toorani and Lakis [19]. Due to the change of the kinematical model the relationships between strains and displacements along the shell reference surface
. It should be also remarked that, differently from the previous works by Tornabene [65,77,78], the displacement field has been improved taking into account the real geometry of the shell and in particular the curvature effect has been directly introduced into the kinematical model as proposed by Toorani and Lakis [19]. Due to the change of the kinematical model the relationships between strains and displacements along the shell reference surface  become the following:
become the following:
 (18)
(18)
that are different from those presented in previous papers [77,78]. In the above Equations (19), the first four strains
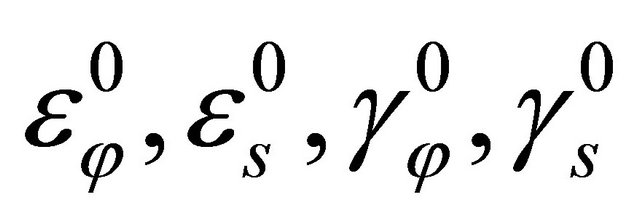 are the in-plane meridian, circumferential and shearing components, and
are the in-plane meridian, circumferential and shearing components, and 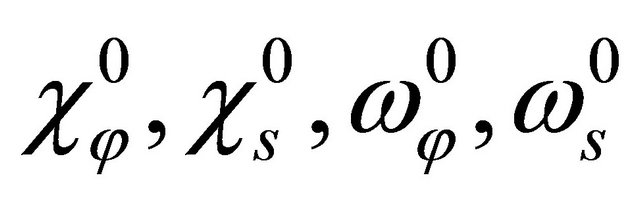 are the analogous curvature changes. The last two components
are the analogous curvature changes. The last two components 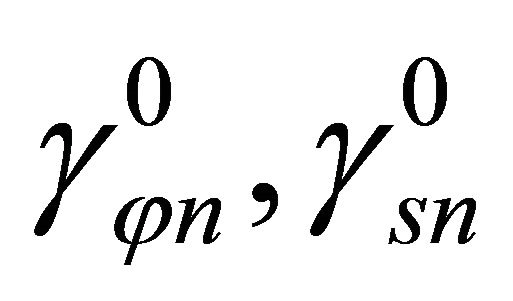 are the transverse shearing strains. The shell composition assumed in the following is a laminated composite linear elastic material. Accordingly, the following constitutive equations relate internal stress resultants and internal couples with generalized strain components (18) on the middle surface:
are the transverse shearing strains. The shell composition assumed in the following is a laminated composite linear elastic material. Accordingly, the following constitutive equations relate internal stress resultants and internal couples with generalized strain components (18) on the middle surface:
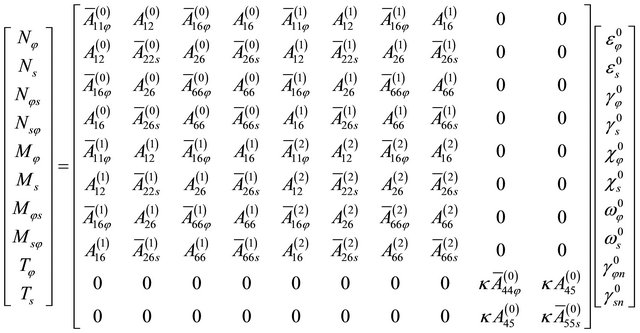 (19)
(19)
where the elastic engineering stiffnesses 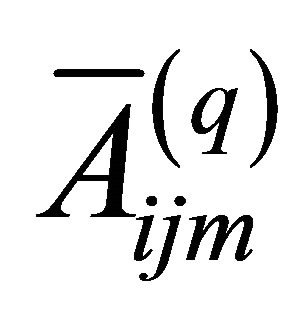 which depend on curvatures are defined as follows (see Appendix for more details):
which depend on curvatures are defined as follows (see Appendix for more details):
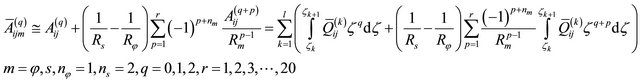 (20)
(20)
Several approaches can be found in literature to evaluate the engineering elastic constants  [7,16-18]. It is worth noting that due to the fact that the elastic engineering stiffnesses
[7,16-18]. It is worth noting that due to the fact that the elastic engineering stiffnesses  depend on curvatures, the corresponding derivatives respect to the co-ordinates along the meridian
depend on curvatures, the corresponding derivatives respect to the co-ordinates along the meridian  and circumferential
and circumferential  directions of the reference surface have to be evaluated. In order to perform this operation, the Differential Quadrature rule [26] is used. Thus, the derivatives of the elastic engineering stiffnesses
directions of the reference surface have to be evaluated. In order to perform this operation, the Differential Quadrature rule [26] is used. Thus, the derivatives of the elastic engineering stiffnesses  are numerically evaluated.
are numerically evaluated.  is the shear correction factor, which is usually taken equal to
is the shear correction factor, which is usually taken equal to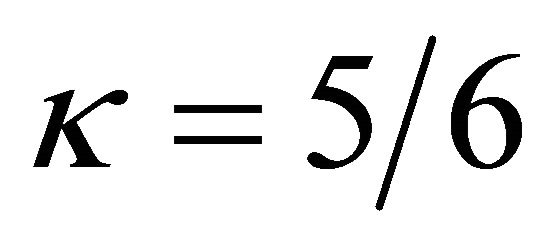 , such as in the present work. In particular, the determination of shear correction factors for composite laminated structures is still an unresolved issue, because these factors depend on various parameters [18]. In Equations (19), the four components
, such as in the present work. In particular, the determination of shear correction factors for composite laminated structures is still an unresolved issue, because these factors depend on various parameters [18]. In Equations (19), the four components 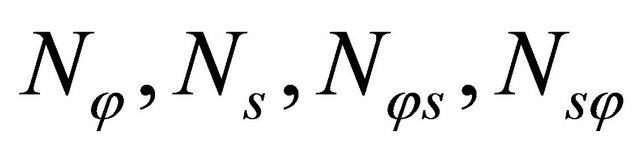 are the in-plane meridian, circumferential and shearing force resultants, and
are the in-plane meridian, circumferential and shearing force resultants, and 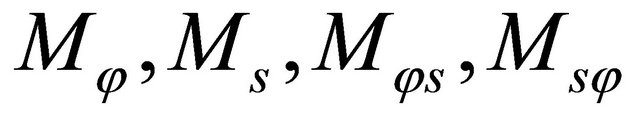 are the analogous couples, while
are the analogous couples, while 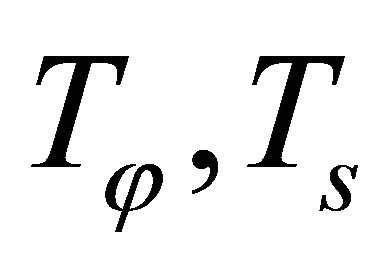 are the transverse shear force resultants. In the above definitions (19) the symmetry of shearing force resultants
are the transverse shear force resultants. In the above definitions (19) the symmetry of shearing force resultants 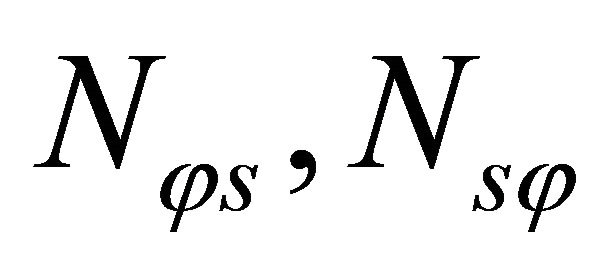 and torsional couples
and torsional couples 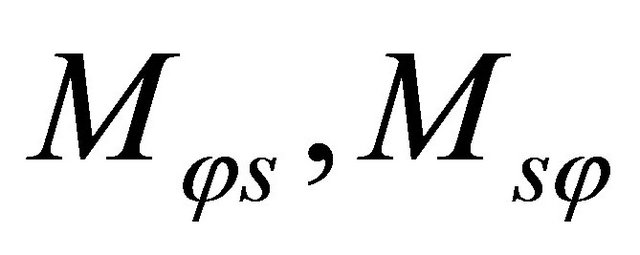 is not assumed as a further hypothesis, as done in Reissner-Mindlin theory. This hypothesis is in fact satisfied only in the case of spherical shells and flat plates. The assumption under discussion is derived from the consideration that ratios
is not assumed as a further hypothesis, as done in Reissner-Mindlin theory. This hypothesis is in fact satisfied only in the case of spherical shells and flat plates. The assumption under discussion is derived from the consideration that ratios 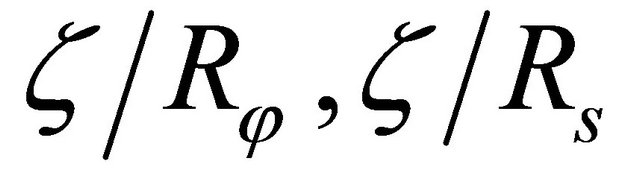 cannot be neglected with respect to unity. For the k-th orthotropic lamina the elastic constants
cannot be neglected with respect to unity. For the k-th orthotropic lamina the elastic constants  in the laminate co-ordinate system
in the laminate co-ordinate system 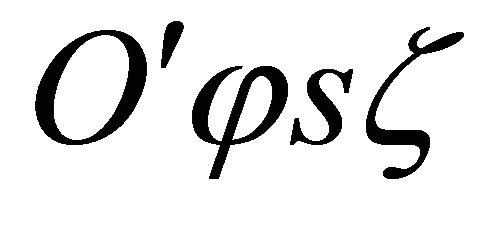 can be written as:
can be written as:
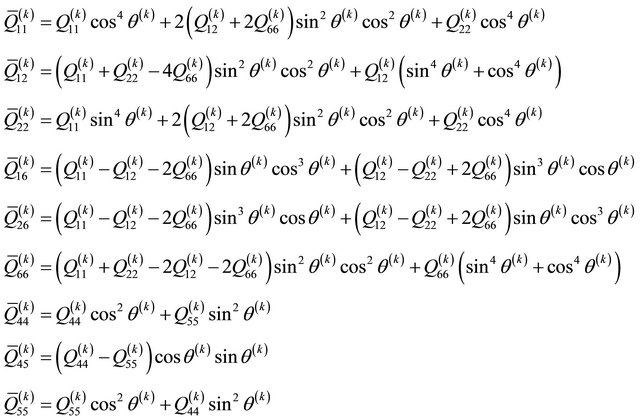 (21)
(21)
where 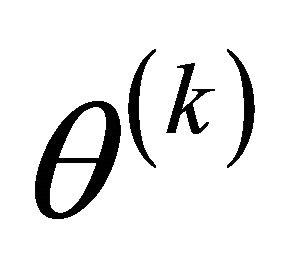 is the orientation angle of the principal material co-ordinate system
is the orientation angle of the principal material co-ordinate system 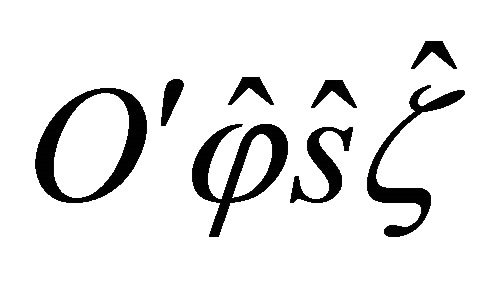 of the k-th orthotropic ply with respect to the laminate co-ordinate system
of the k-th orthotropic ply with respect to the laminate co-ordinate system 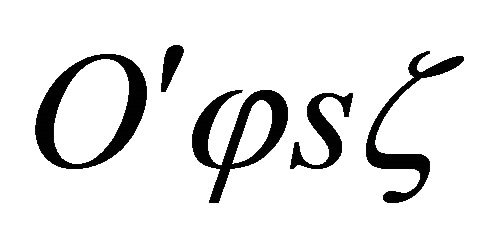 . Furthermore, the elastic constants
. Furthermore, the elastic constants 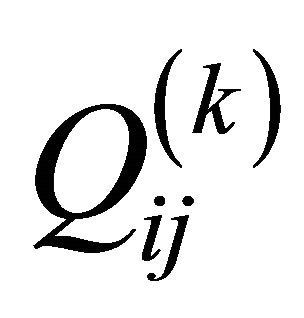 in the material co-ordinate system
in the material co-ordinate system 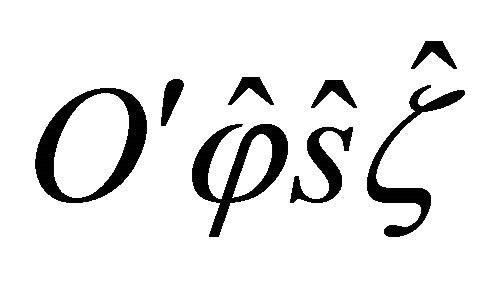 are expressed as follows:
are expressed as follows:
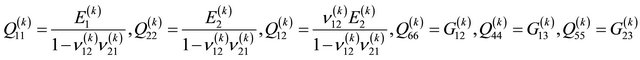 (22)
(22)
where 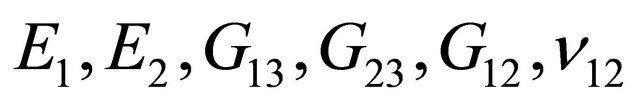 are the engineering parameters of the k-th lamina. It should be noted that for a complete characterization of an orthotropic material, the parameters
are the engineering parameters of the k-th lamina. It should be noted that for a complete characterization of an orthotropic material, the parameters 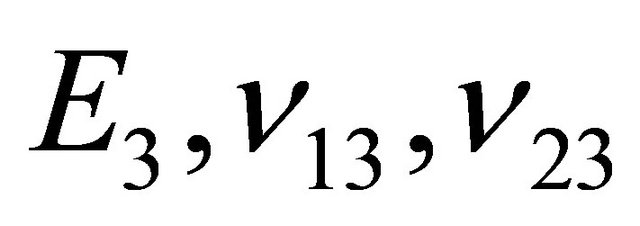 have to be taken into account, as well-known. Following the virtual work principle in dynamic version, and remembering the Gauss-Codazzi relations for the shells of revolution (12), five equations of dynamic equilibrium in terms of internal actions can be written for the revolution shell element:
have to be taken into account, as well-known. Following the virtual work principle in dynamic version, and remembering the Gauss-Codazzi relations for the shells of revolution (12), five equations of dynamic equilibrium in terms of internal actions can be written for the revolution shell element:
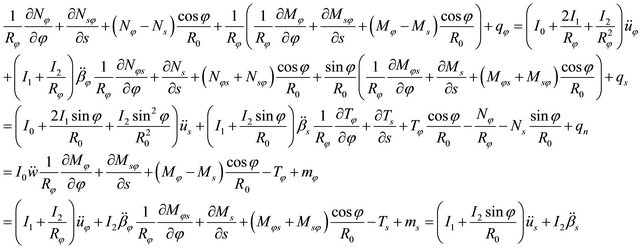 (23)
(23)
where:
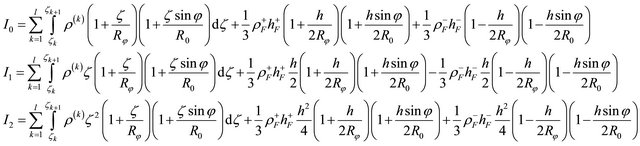 (24)
(24)
are the mass inertias and 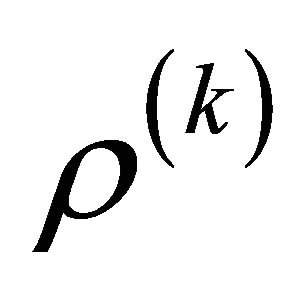 is the mass density of the material per unit of volume of the k-th ply, while
is the mass density of the material per unit of volume of the k-th ply, while 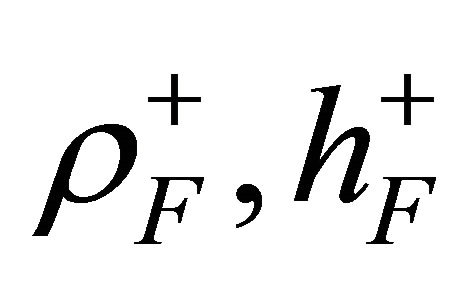 and
and 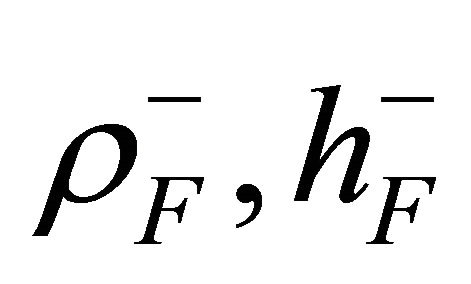 are the mass density of the material per unit of volume and the thickness of the elastic foundation at the top and the bottom surface of the shell, respectively. The first three equations (23) represent translational equilibrium along meridian
are the mass density of the material per unit of volume and the thickness of the elastic foundation at the top and the bottom surface of the shell, respectively. The first three equations (23) represent translational equilibrium along meridian , circumferential
, circumferential 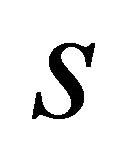 and normal
and normal  directions, while the last two are rotational equilibrium equations about the
directions, while the last two are rotational equilibrium equations about the 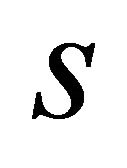 and
and  directions, respectively. Furthermore, the generalized external forces
directions, respectively. Furthermore, the generalized external forces 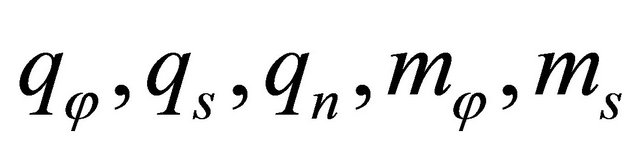 due to the external forces and the Winkler-Pasternak elastic foundation acting on the top and bottom surfaces of the shell can be evaluated using the static equivalence principle [12,79,83] and can be written on the reference surface of the doubly-curved shell as follows:
due to the external forces and the Winkler-Pasternak elastic foundation acting on the top and bottom surfaces of the shell can be evaluated using the static equivalence principle [12,79,83] and can be written on the reference surface of the doubly-curved shell as follows:




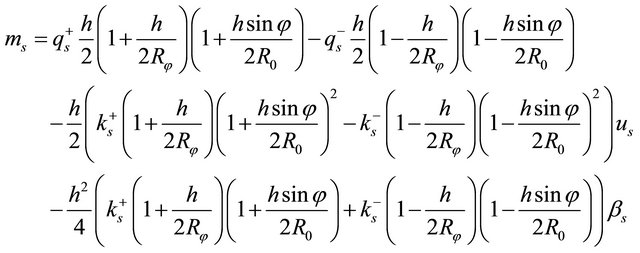 (25)
(25)
where 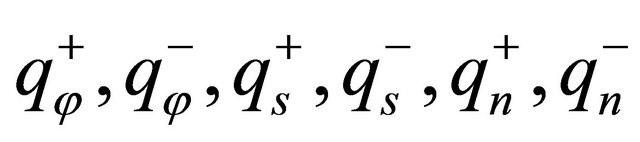 are the external forces and
are the external forces and 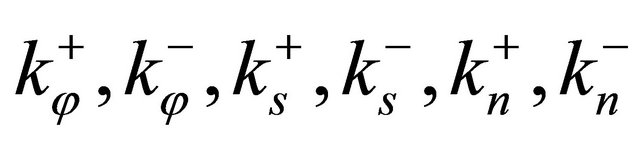 are the Winkler elastic stiffnesses in the three principal directions
are the Winkler elastic stiffnesses in the three principal directions 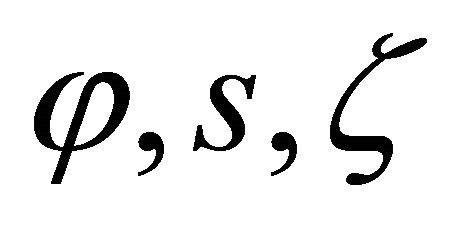 at the top and the bottom surface of the shell, respectively;
at the top and the bottom surface of the shell, respectively; 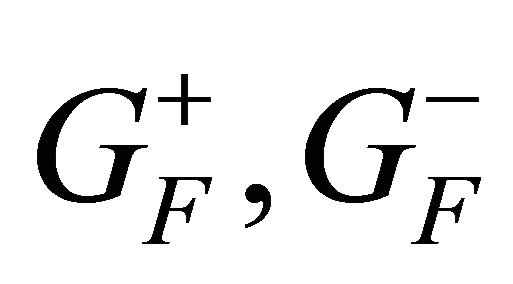 are the shear modulus of the Pasternak elastic foundation at the top and the bottom surface of the shell. It is worth noting that the formulation of the Winkler-Pasternak foundation is based on the first-order approximated assumption that the foundation is a homogeneous material of uniform thickness
are the shear modulus of the Pasternak elastic foundation at the top and the bottom surface of the shell. It is worth noting that the formulation of the Winkler-Pasternak foundation is based on the first-order approximated assumption that the foundation is a homogeneous material of uniform thickness 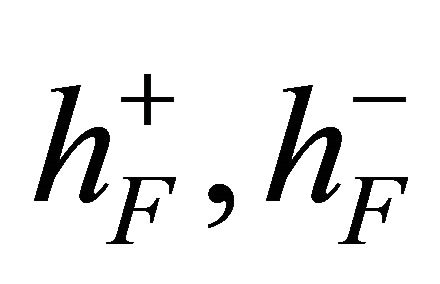 [12,79,83]. Furthermore, as additional hypothesis, the effect of the damping of the foundation is neglected. The three basic set of equations, namely the kinematic (18), constitutive (19) and motion (23) equations may be combined to give the fundamental system of equations, also known as the governing system of equations. By replacing the kinematic equations (18) into the constitutive equations (19) and the result of this substitution into the motion equations (23), the complete equations of motion in terms of displacements can be written as:
[12,79,83]. Furthermore, as additional hypothesis, the effect of the damping of the foundation is neglected. The three basic set of equations, namely the kinematic (18), constitutive (19) and motion (23) equations may be combined to give the fundamental system of equations, also known as the governing system of equations. By replacing the kinematic equations (18) into the constitutive equations (19) and the result of this substitution into the motion equations (23), the complete equations of motion in terms of displacements can be written as:
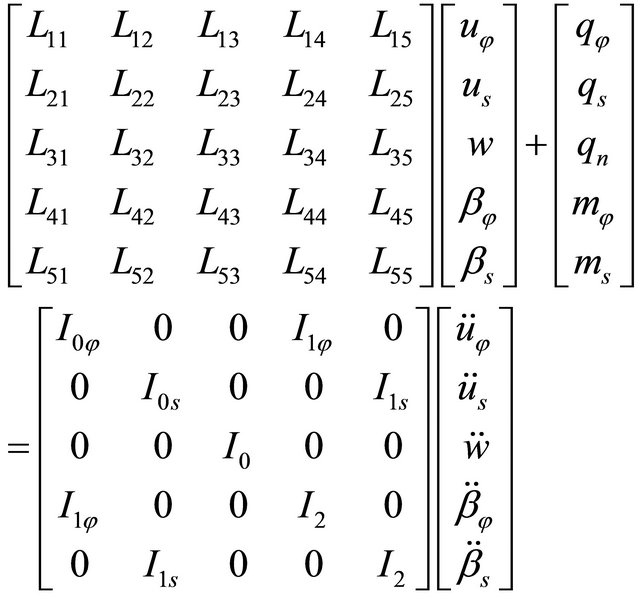 (26)
(26)
where 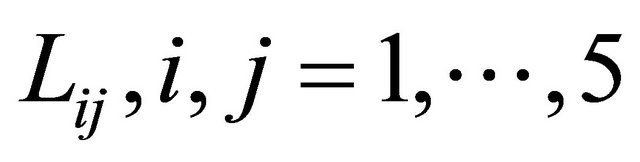 are the equilibrium operators and the new mass inertias are defined as follows:
are the equilibrium operators and the new mass inertias are defined as follows:
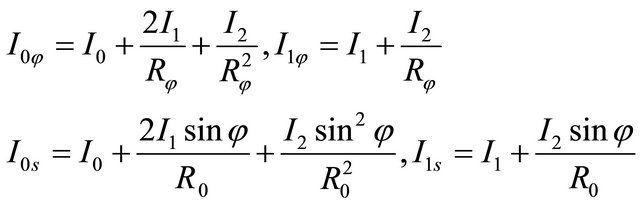 (27)
(27)
It is worth noting that, differently from previous works by Tornabene [77,78], the mass matrix and the equilibrium operators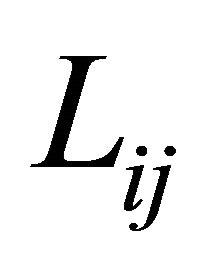 , introduced in Equation (27), have changed due to the choice of using the new kinematical model (18). Furthermore, the second derivative of the principal radius
, introduced in Equation (27), have changed due to the choice of using the new kinematical model (18). Furthermore, the second derivative of the principal radius 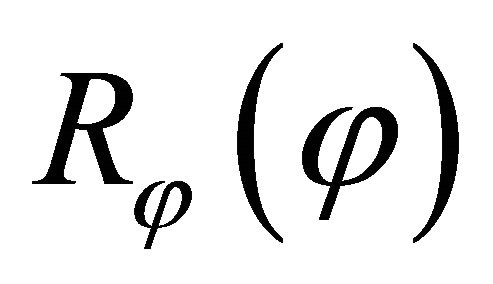 respect to
respect to  has to be evaluated, as it can be inferred from the explicit form of the equilibrium operators
has to be evaluated, as it can be inferred from the explicit form of the equilibrium operators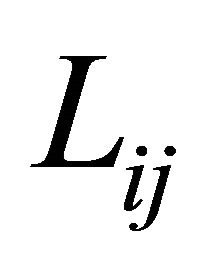 . Three types of boundary conditions are considered, namely the fully clamped edge boundary condition (C), soft simply supported edge boundary conditions (S) and the free edge boundary condition (F). The equations describing the boundary conditions can be written as follows:
. Three types of boundary conditions are considered, namely the fully clamped edge boundary condition (C), soft simply supported edge boundary conditions (S) and the free edge boundary condition (F). The equations describing the boundary conditions can be written as follows:
Clamped edge boundary conditions (C)
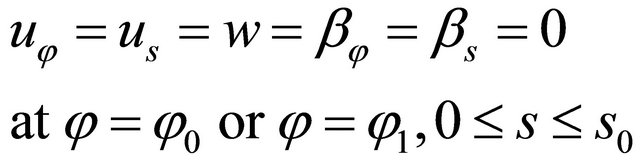 (28)
(28)
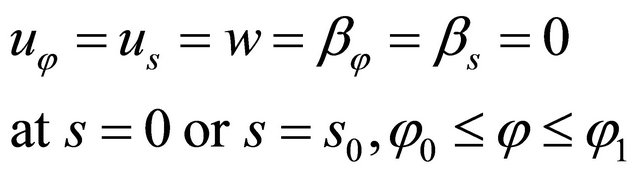 (29)
(29)
Soft simply supported edge boundary conditions (S)
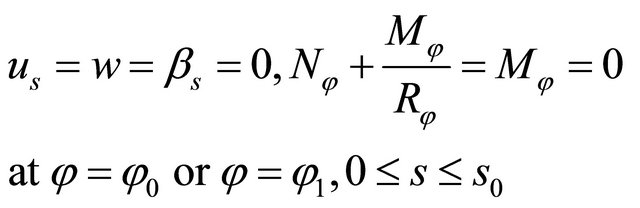 (30)
(30)
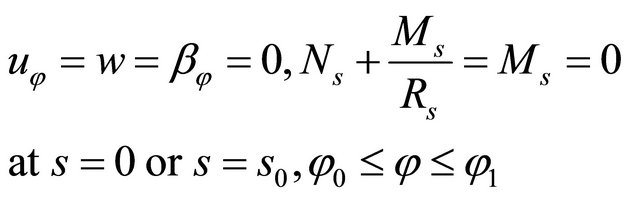 (31)
(31)
Free edge boundary conditions (F)
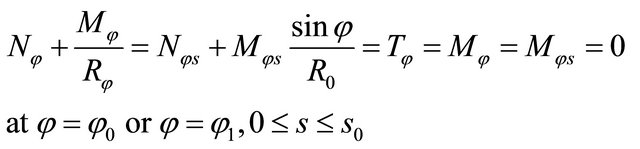 (32)
(32)
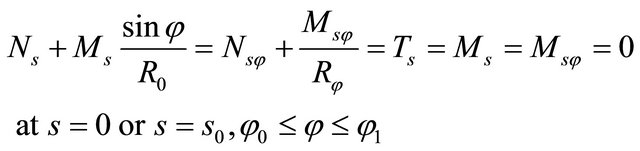 (33)
(33)
where 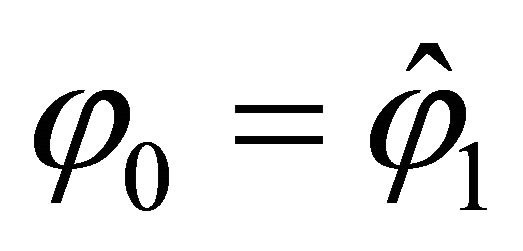 and
and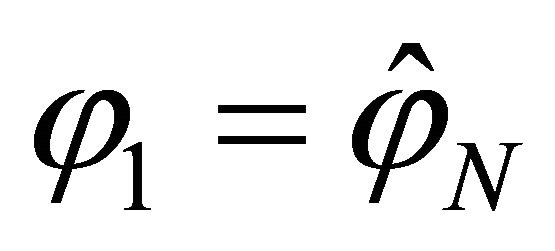 . In addition to the external boundary conditions, the kinematic and physical compatibility conditions should be satisfied at the common closing meridians with
. In addition to the external boundary conditions, the kinematic and physical compatibility conditions should be satisfied at the common closing meridians with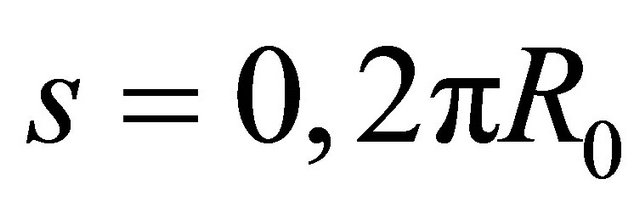 , if a complete shell of revolution is considered. The kinematic compatibility conditions include the continuity of displacements. The physical compatibility conditions can be only represented by the five continuous conditions for the generalized stress resultants. To consider complete revolute shells, it is necessary to implement the kinematic and physical compatibility conditions between the two computational meridians with
, if a complete shell of revolution is considered. The kinematic compatibility conditions include the continuity of displacements. The physical compatibility conditions can be only represented by the five continuous conditions for the generalized stress resultants. To consider complete revolute shells, it is necessary to implement the kinematic and physical compatibility conditions between the two computational meridians with 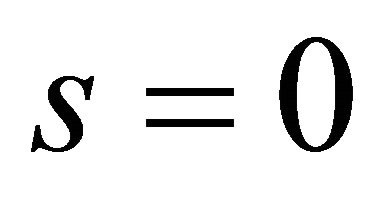 and with
and with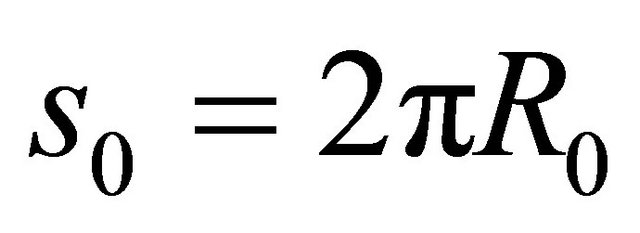 :
:
Kinematic compatibility conditions along the closing meridian 
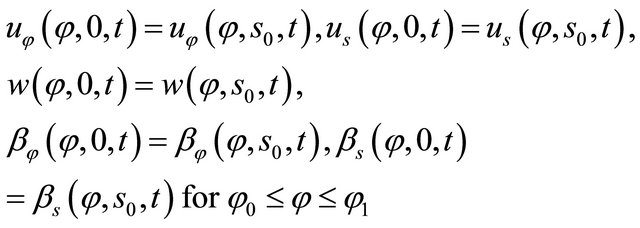 (34)
(34)
Physical compatibility conditions along the closing meridian
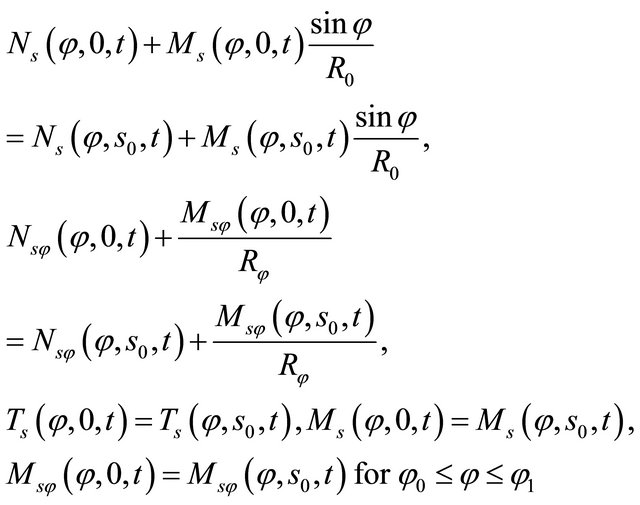 (35)
(35)
where 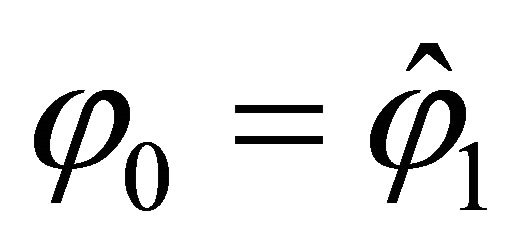 and
and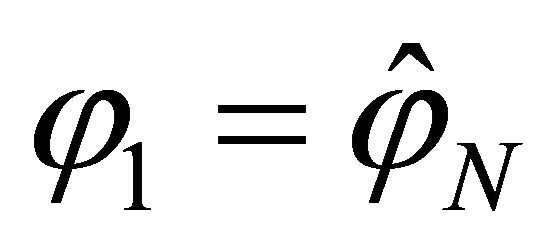 . In an analogous way, in order to consider a toroidal shell of revolution, it is necessary to implement the kinematic and physical compatibility conditions between the two computational parallels with
. In an analogous way, in order to consider a toroidal shell of revolution, it is necessary to implement the kinematic and physical compatibility conditions between the two computational parallels with 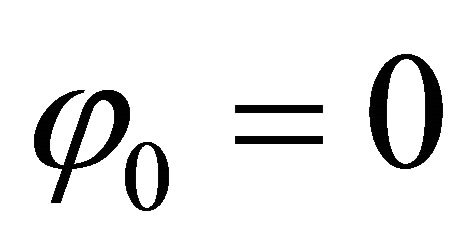 and with
and with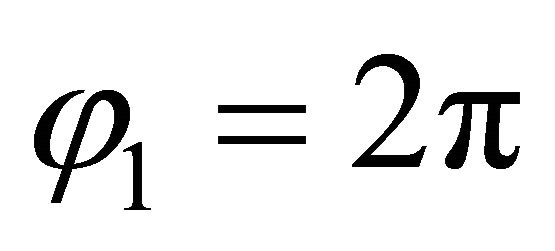 :
:
Kinematic compatibility conditions along the closing parallel 
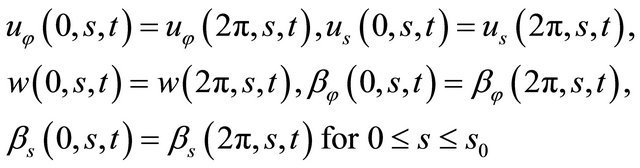 (36)
(36)
Physical compatibility conditions along the closing parallel
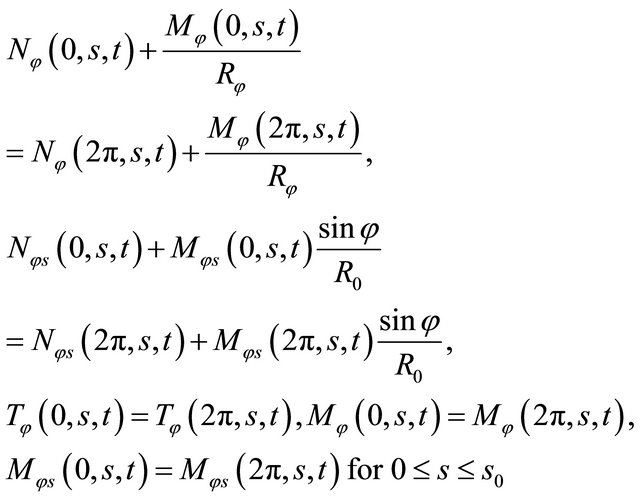 (37)
(37)
3. Numerical Implementation
The Generalized Differential Quadrature method will be used to discretize the derivatives in the governing equations in terms of displacements as well as boundary and compatibility conditions. Since a review of the GDQ Method is presented in Tornabene [65,83], the same approach is used in the present work about the GDQ technique. The Chebyshev-Gauss-Lobatto (C-G-L) grid distribution is assumed. Since the co-ordinates of the grid points of the reference surface in the  direction are introduced in Equation (9), then the co-ordinates of the grid points in the
direction are introduced in Equation (9), then the co-ordinates of the grid points in the 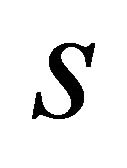 direction are the following:
direction are the following:
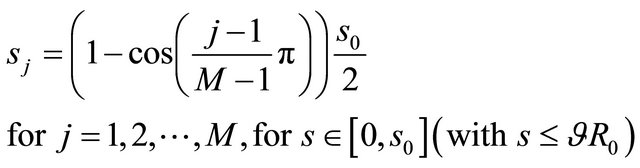 (38)
(38)
where 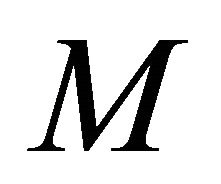 is the total number of sampling points used to discretize the domain in
is the total number of sampling points used to discretize the domain in 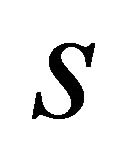 direction of the doublycurved shell. It has been proven that for the Lagrange interpolating polynomials, the Chebyshev-Gauss-Lobatto sampling points rule guarantees convergence and efficiency to the GDQ technique [57-59,63,83]. For the static analysis, when the inertias are set to zero, the GDQ procedure enables to write the equations of equilibrium (26) in discrete form, transforming each space derivative into a weighted sum of node values of independent variables. Each approximated equation is valid in a single sampling point. Thus, the whole system of differential equations has been discretized and the global assembling leads to the following set of linear algebraic equations:
direction of the doublycurved shell. It has been proven that for the Lagrange interpolating polynomials, the Chebyshev-Gauss-Lobatto sampling points rule guarantees convergence and efficiency to the GDQ technique [57-59,63,83]. For the static analysis, when the inertias are set to zero, the GDQ procedure enables to write the equations of equilibrium (26) in discrete form, transforming each space derivative into a weighted sum of node values of independent variables. Each approximated equation is valid in a single sampling point. Thus, the whole system of differential equations has been discretized and the global assembling leads to the following set of linear algebraic equations:
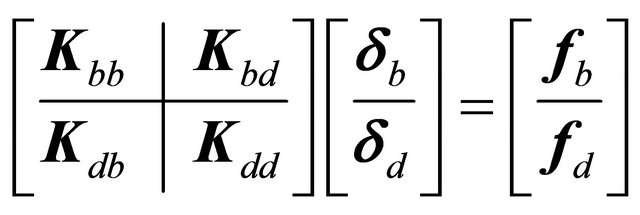 (39)
(39)
In the above mentioned matrices and vectors, the partitioning is set forth by subscripts  and
and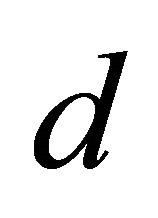 , referring to the system degrees of freedom and standing for boundary and domain, respectively. In this sense,
, referring to the system degrees of freedom and standing for boundary and domain, respectively. In this sense,  -equations represent the discrete boundary conditions, which are valid only for the points lying on constrained edges of the shell; while
-equations represent the discrete boundary conditions, which are valid only for the points lying on constrained edges of the shell; while 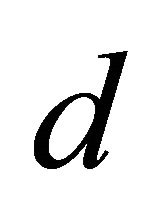 -equations are the equilibrium equations, assigned to the interior nodes. In order to make the computation more efficient, static condensation of non-domain degrees of freedom is performed:
-equations are the equilibrium equations, assigned to the interior nodes. In order to make the computation more efficient, static condensation of non-domain degrees of freedom is performed:
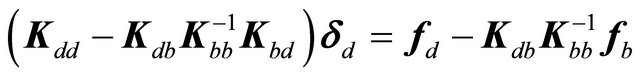 (40)
(40)
The deflection of the structures considered can be determined by solving the linear algebraic problem (40). In particular, the solution procedure by means of the GDQ technique has been implemented in a MATLAB code. Otherwise, when the external forces 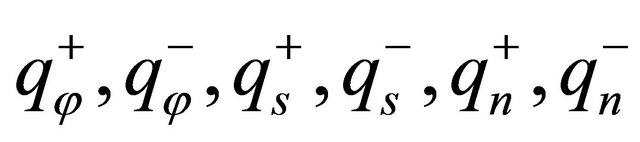 are set to zero, the free vibration of laminated composite doubly-curved shells and panels of revolution can be studied. Using the method of variable separation, it is possible to seek solutions that are harmonic in time and whose frequency is
are set to zero, the free vibration of laminated composite doubly-curved shells and panels of revolution can be studied. Using the method of variable separation, it is possible to seek solutions that are harmonic in time and whose frequency is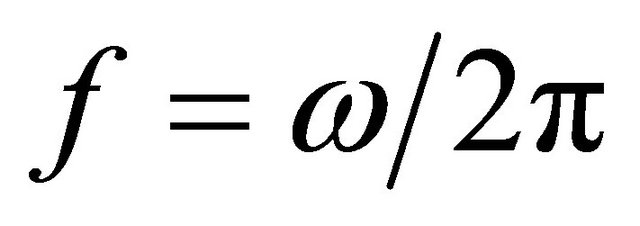 . The displacement field can be written as follows:
. The displacement field can be written as follows:
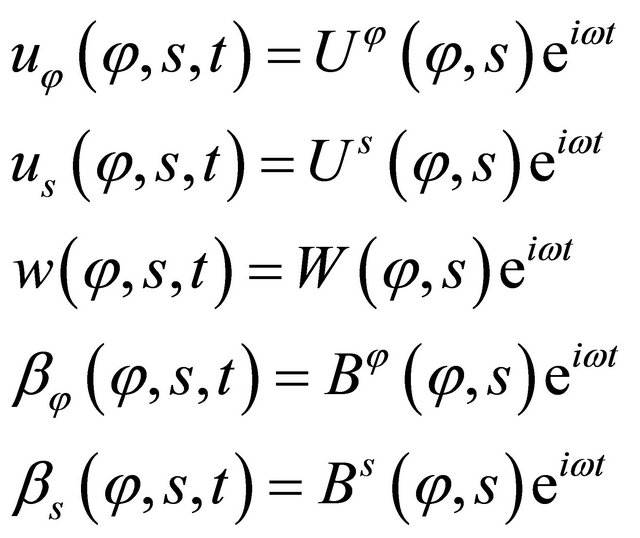 (41)
(41)
where the vibration spatial amplitude values 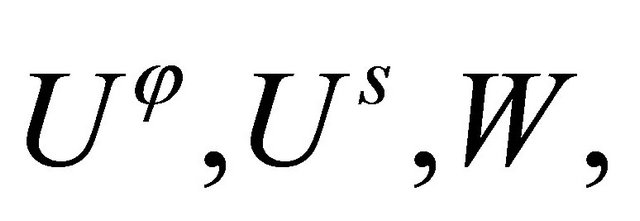
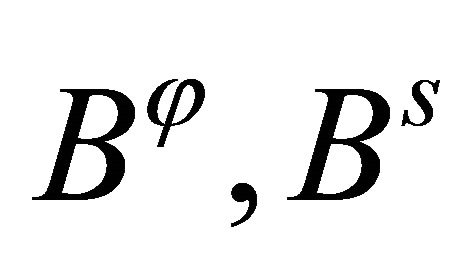 fulfill the fundamental differential system. Thus, the whole system of differential equations has been discretized and the global assembling leads to the following linear eigenvalue problem:
fulfill the fundamental differential system. Thus, the whole system of differential equations has been discretized and the global assembling leads to the following linear eigenvalue problem:
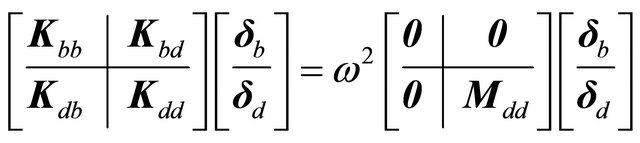 (42)
(42)
In order to make the computation more efficient, kinematic condensation of non-domain degrees of freedom is performed:
 (43)
(43)
The natural frequencies of the structure considered can be determined by solving the standard eigenvalue problem (43). In particular, the solution procedure by means of the GDQ technique has been implemented in a MATLAB code. Finally, the results in terms of frequencies are obtained using the eigs function of MATLAB software. More details regarding the way to obtained the Equations (40) and (43) can be found in the previous works [57-59,63,65-68,83]. It is worth noting that, with the present approach, differing from the finite element method, no integration occurs prior to the global assembly of the linear system, and this approach leads to a further computational cost saving in favor of the Differential Quadrature technique.
4. Numerical Results
In the present paragraph, some results and considerations about the static analysis and the free vibration problem of laminated composite doubly-curved shells and panels of revolution are presented. The analysis has been carried out by means of numerical procedures illustrated above. One of the aims of this paper is to compare results obtained through the GDQ method with the ones obtained through finite element techniques. In order to verify the accuracy of the present method, some comparisons and tests have been performed. Extensive attempts to validate the numerical procedure have been made for the isotropic and anisotropic cases and can be found in the Ph.D. Thesis by Tornabene [57] and in the book by Tornabene [83]. In this work, the static deflection and the frequency parameters evaluated by the present formulation are in good agreement with the results obtained with the finite element method. The geometrical boundary conditions for a panel are identified by the following convention. For example, symbolism CSCF shows that the edges  are clamped, simply supported, clamped and free, respectively. On the contrary, for a complete shell of revolution or for a toroidal shell, symbolism CF shows that the edges
are clamped, simply supported, clamped and free, respectively. On the contrary, for a complete shell of revolution or for a toroidal shell, symbolism CF shows that the edges  and
and 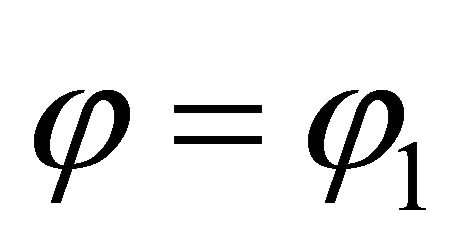 or
or 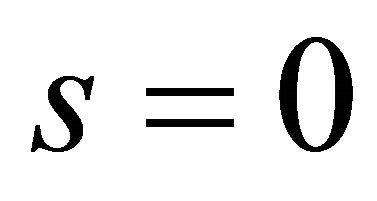 and
and 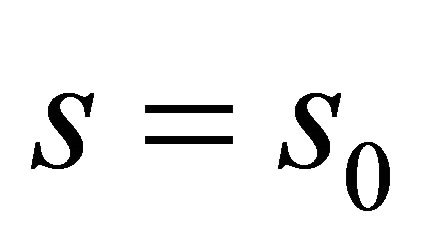 are clamped and free, respectively. The missing boundary conditions are the kinematic and physical compatibility conditions that are applied at the same closing meridians for
are clamped and free, respectively. The missing boundary conditions are the kinematic and physical compatibility conditions that are applied at the same closing meridians for 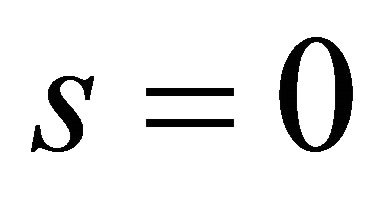 and
and 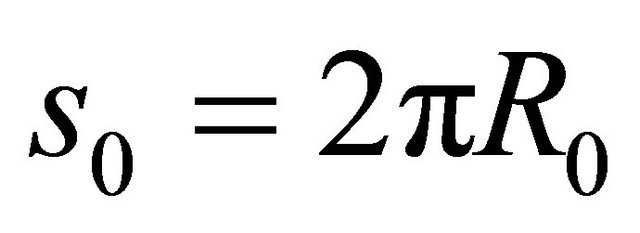 or at the same closing parallels for
or at the same closing parallels for 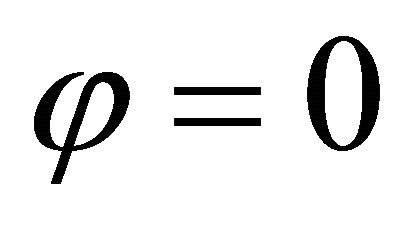 and
and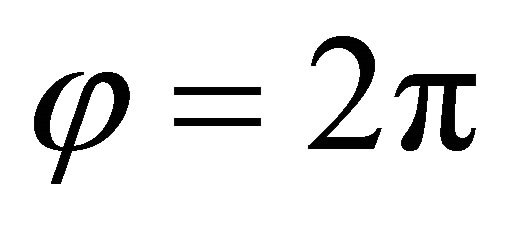 , respectively. Table 1 presents the static deflection at the point
, respectively. Table 1 presents the static deflection at the point  for a SSSS spherical panel resting on elastic foundation and subjected to a uniformly distributed load
for a SSSS spherical panel resting on elastic foundation and subjected to a uniformly distributed load 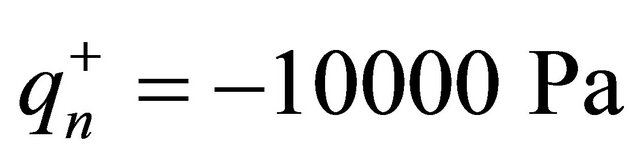 at the top surface by considering different lamination schemes. As can be seen, the numerical results show an excellent agreement for all the cases considered. GDQ results are compared with the FEM results obtained with Straus 7 commercial software using 8 node parabolic shell elements. In order to illustrate the effect of the foundation Figures 4 and 5 show the stress resultants for a
at the top surface by considering different lamination schemes. As can be seen, the numerical results show an excellent agreement for all the cases considered. GDQ results are compared with the FEM results obtained with Straus 7 commercial software using 8 node parabolic shell elements. In order to illustrate the effect of the foundation Figures 4 and 5 show the stress resultants for a  CCCC spherical panel subjected to a uniformly distributed load
CCCC spherical panel subjected to a uniformly distributed load 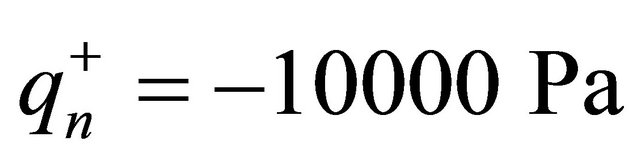 at the top surface. Figure 4 illustrates the stress resultants obtained without considering the foundation, while Figure 5 presents the same quantities obtained considering the elastic foundation. The geometrical and material properties are the same reported in
at the top surface. Figure 4 illustrates the stress resultants obtained without considering the foundation, while Figure 5 presents the same quantities obtained considering the elastic foundation. The geometrical and material properties are the same reported in
Table 1. Static deflection for a SSSS spherical panel at the point 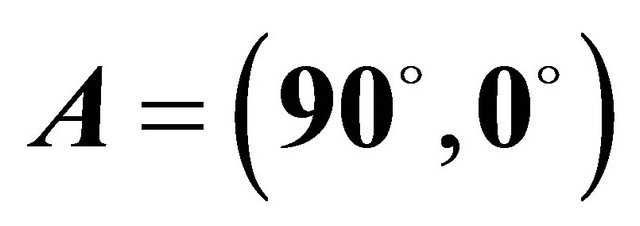 resting on elastic foundation and subjected to a uniformly distributed load
resting on elastic foundation and subjected to a uniformly distributed load 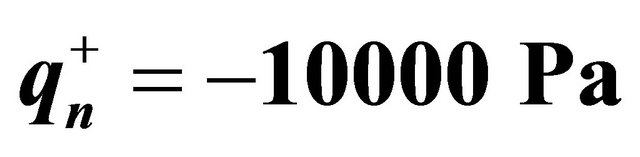 at the top surface.
at the top surface.

*Geometric characteristics: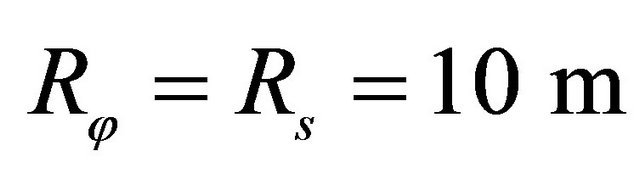 ,
, 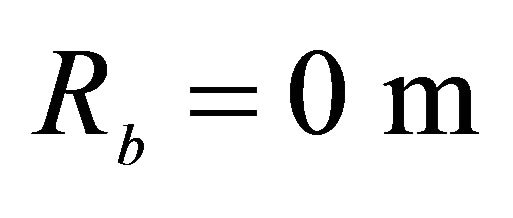 ,
, 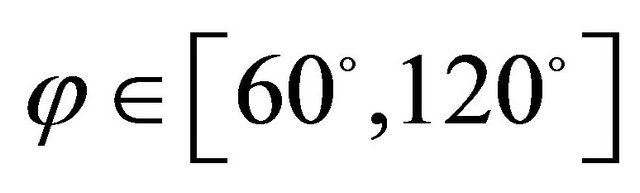 ,
, 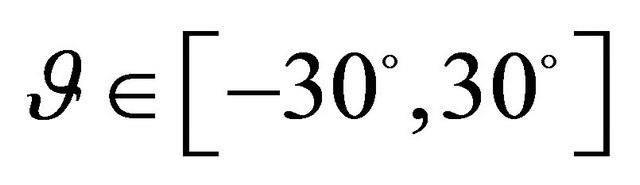 ,
, 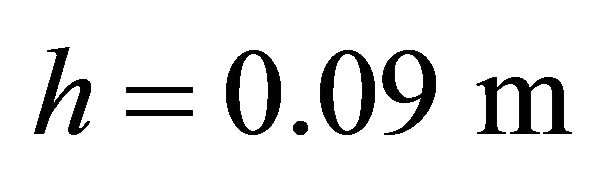 , Isotropic material:
, Isotropic material: ,
, 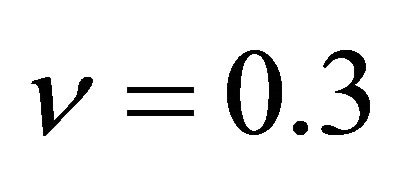 ,
, 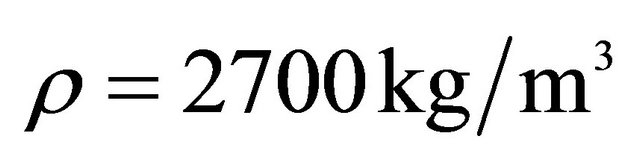 , Orthotropic material:
, Orthotropic material: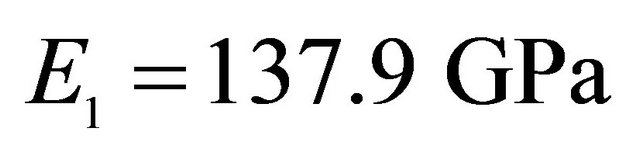 ,
,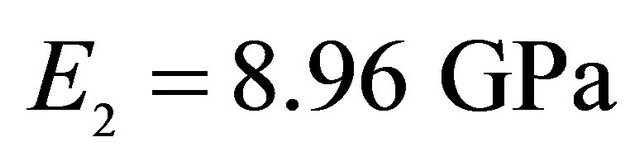 ,
,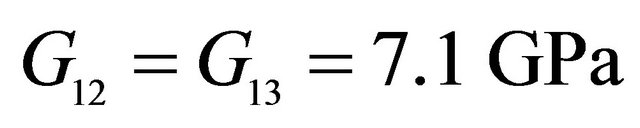 ,
,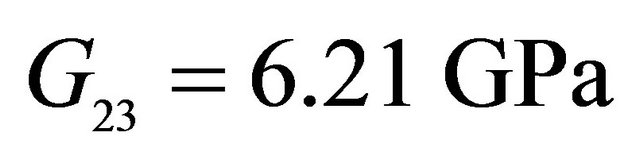 ,
,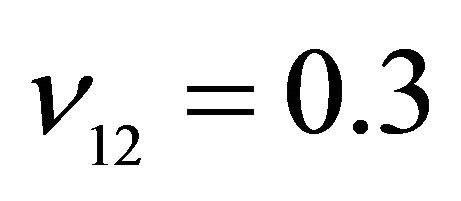 ,
,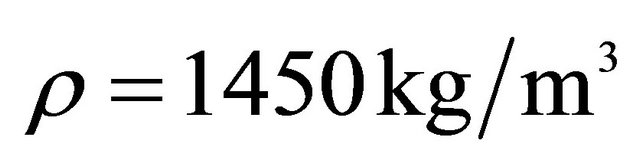 .
.
Figure 4. Stress resultants for a  CCCC spherical panel with a uniformly distributed load
CCCC spherical panel with a uniformly distributed load 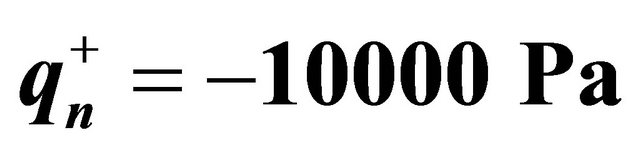 at the top surface and without elastic foundation.
at the top surface and without elastic foundation.
Table 1. As can be seen from the figures, the effect of the foundation reduces the stress resultants as expected. In Tables 2-4, the results, in terms of first ten frequencies obtained by the GDQ Method for the General Shell Theory (GST) presented above with and without elastic foundations, are compared with the FEM results obtained with Straus 7 commercial software. The details regarding the geometry and the material properties are reported in
Figure 5. Stress resultants for a  CCCC spherical panel with a uniformly distributed load
CCCC spherical panel with a uniformly distributed load 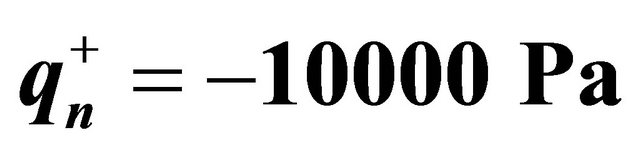 at the top surface resting on Winkler-Pasternak elastic foundation:
at the top surface resting on Winkler-Pasternak elastic foundation: 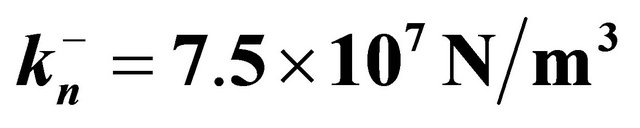 and
and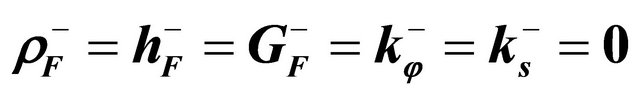 .
.
tables. For the present GDQ results, the grid distributions (9) and (38) with 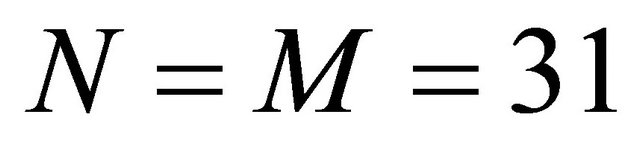 have been considered. Tables 2-4 present the first ten frequencies for a SSSS spherical panel characterized by
have been considered. Tables 2-4 present the first ten frequencies for a SSSS spherical panel characterized by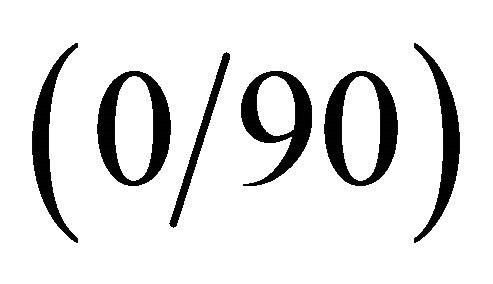 ,
, 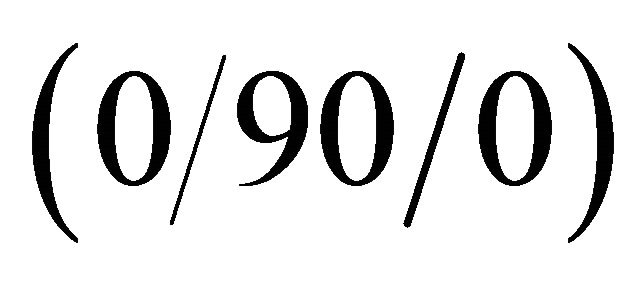 and
and  lamination scheme, respectively. As can be seen, the numerical results from the GDQ methodology are very close to those obtained by the commercial program and show an excellent agreement. Tables 5-7 pre-
lamination scheme, respectively. As can be seen, the numerical results from the GDQ methodology are very close to those obtained by the commercial program and show an excellent agreement. Tables 5-7 pre-
Table 2. First ten frequencies for a 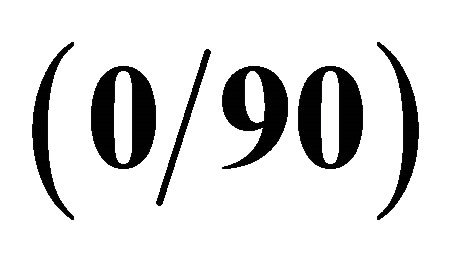 SSSS spherical panel resting on elastic foundation.
SSSS spherical panel resting on elastic foundation.

*Geometric characteristics: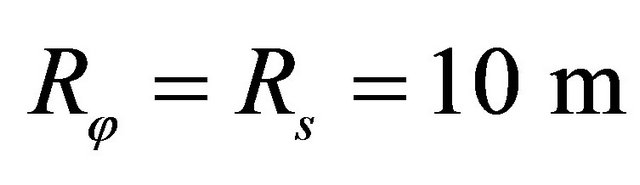 ,
, 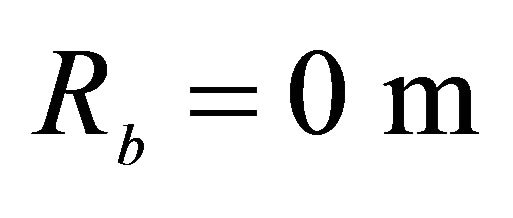 ,
, 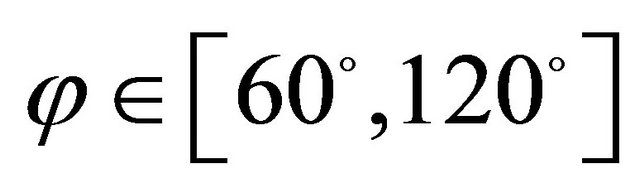 ,
, 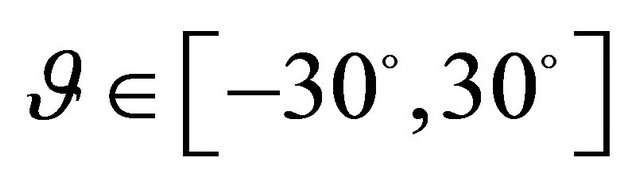 ,
, 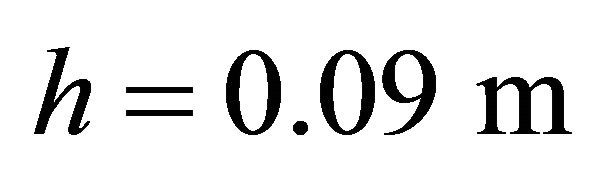 , Orthotropic material:
, Orthotropic material: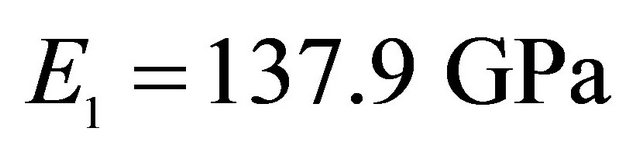 ,
, 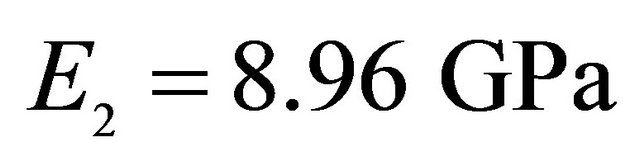 ,
, 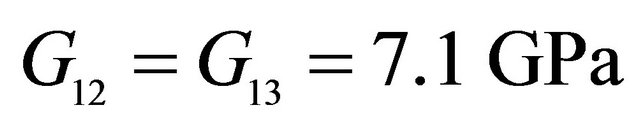 ,
, 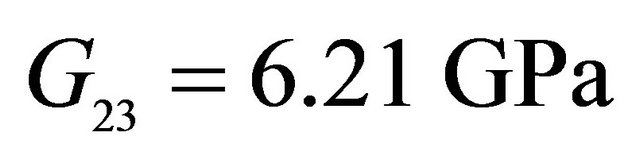 ,
, 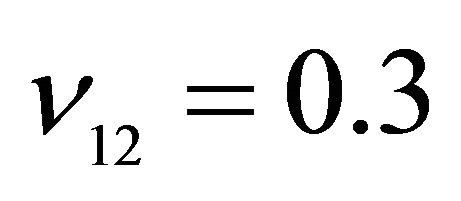 ,
,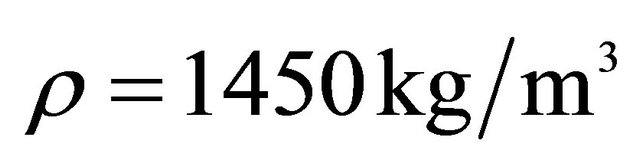 .
.
Table 3. First ten frequencies for a  SSSS spherical panel resting on elastic foundation.
SSSS spherical panel resting on elastic foundation.

*Geometric characteristics: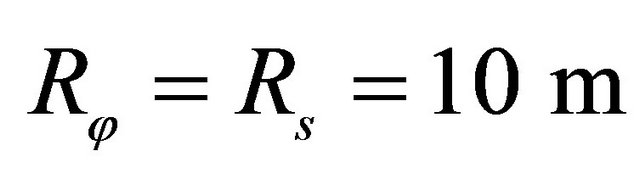 ,
, 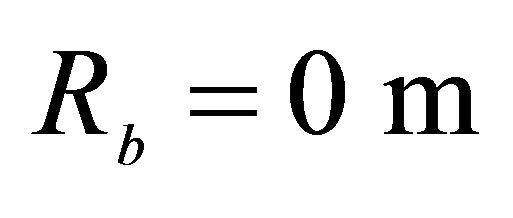 ,
, 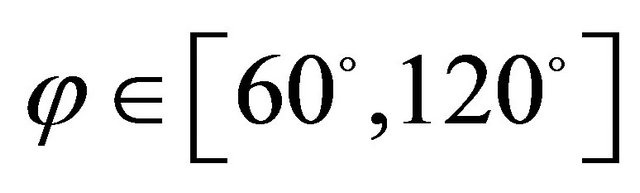 ,
, 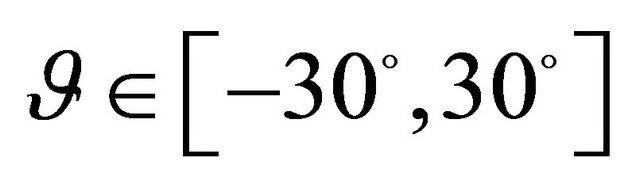 ,
, 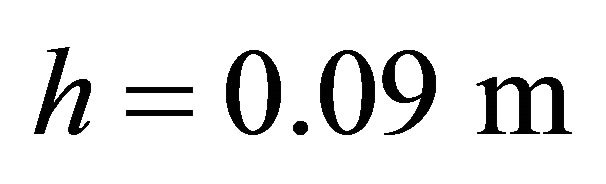 , Orthotropic material:
, Orthotropic material: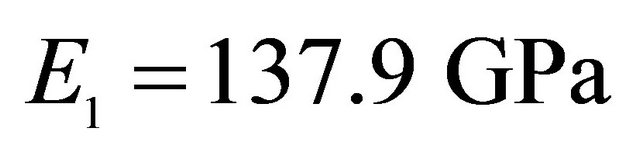 ,
, 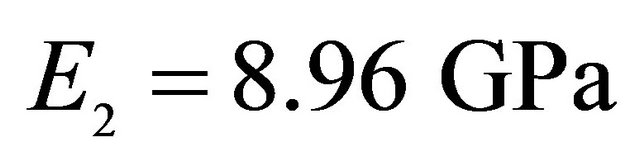 ,
, 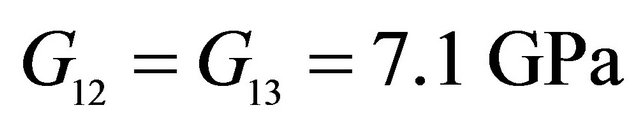 ,
, 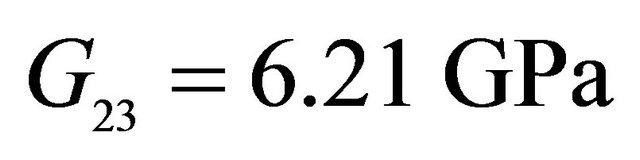 ,
, 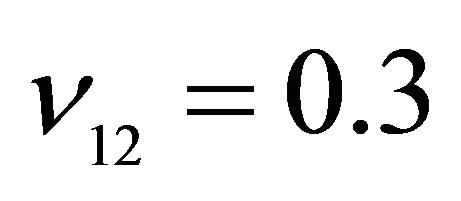 ,
, .
.
Table 4. First ten frequencies for a  SSSS spherical panel resting on elastic foundation.
SSSS spherical panel resting on elastic foundation.

*Geometric characteristics: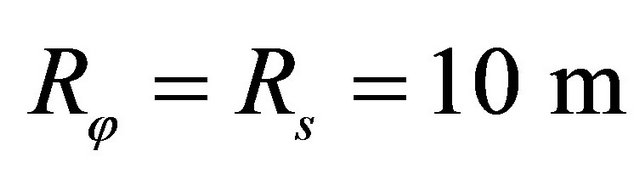 ,
, 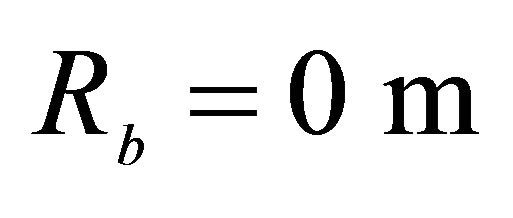 ,
, 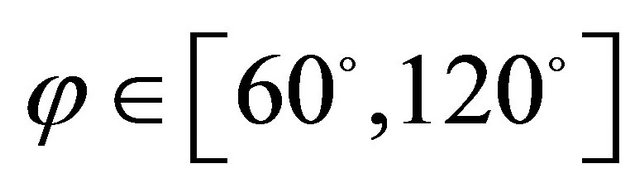 ,
,  ,
,  , Orthotropic material:
, Orthotropic material: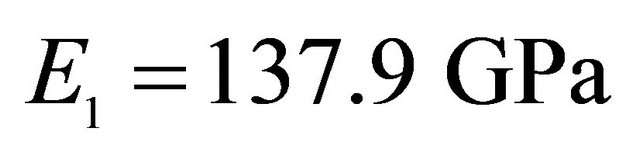 ,
, 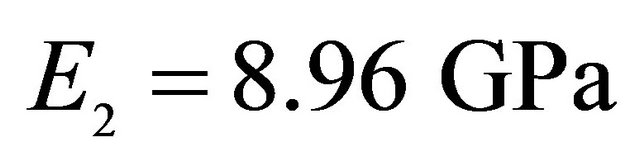 ,
, 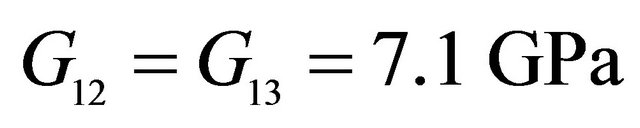 ,
, 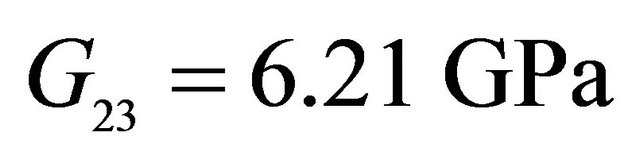 ,
, 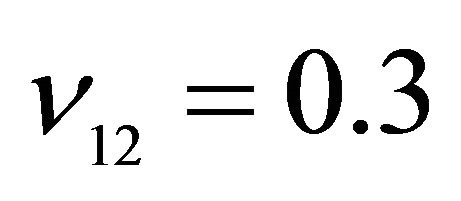 ,
,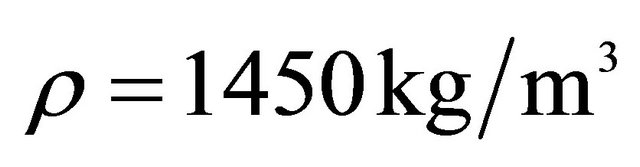 .
.
sent new results regarding different anisotropic doublycurved shells and panels of revolution resting on Winkler-Pasternak elastic foundations. Tables 5-7 are divided in different columns where each effect of the elastic foundation is considered. At first, the effect of the Winkler modulus on free vibrations has been investigated and compared to the case without the elastic foundation. As can be seen from results, the Winkler foundation increases the stiffness of the structure. The same effect is shown by introducing the Pasternak shear modulus. In addition to these two effects the inertia of the foundation is considered. As expected, the inertia effect increases the mass of the structure and reduces the frequencies. Finally, the Winkler foundation in meridian and circumferential directions is introduced. As can be inferred, also in this case the stiffness of the structure is increased. Table 5 presents the effects under consideration for the CC complete shell characterized by the 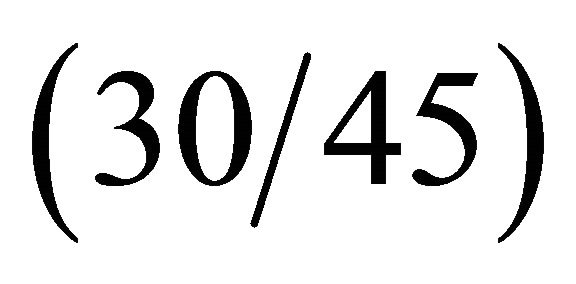 lamination scheme. In this case, the foundation acts on the top surface of the shell. Differently from previous case, Tables 6 and 7 show the first ten frequencies for the
lamination scheme. In this case, the foundation acts on the top surface of the shell. Differently from previous case, Tables 6 and 7 show the first ten frequencies for the 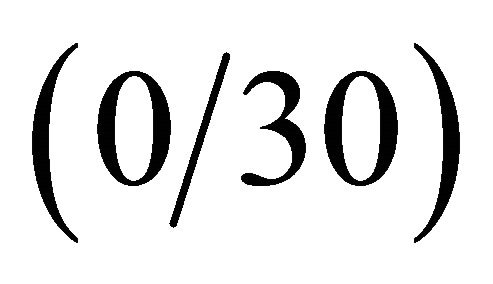 CCCC laminated composite panel and for the
CCCC laminated composite panel and for the  FC laminated composite shell resting on an elastic foundation acting on the bottom surface. Also for these cases, the effect of the initial curvature is considered by comparing the present General Shell Theory (GST) and the Reissner-Mindlin (RM) theory. Thus, as regarding the influence of the initial curvature, it is worth noting that the difference between the two theories considered is low for all the laminated composite doubly-curved structures analyzed. Finally, in Figures 6 and 7, there are reported the first six mode shapes for some of the structures considered above. In particular, for the complete shells of revolution there are some symmetrical mode shapes due to the symmetry of the problem considered in 3D space. In these cases, the symmetrical mode shapes are summarized in one figure. The mode shapes of all the structures have been evaluated by the authors. By using the authors’ MATLAB code, these mode shapes have been reconstructed in three-dimensional view by means of considering the displacement field (17) after solving the eigenvalue problem (43). In addition, Hosseini-Hashemi et al. [86] (see table 3) and Zhao and Liew [87] (see Table 6) have compared their results, obtained with a semi analytical method and produced by a meshless method, with those results presented in the articles by Tornabene [65] and by Tornabene et al. [69], respectively. Since the code used to obtain the previous results by Tornabene [65] and Tornabene et al. [69] is similar to the code used to obtain all the results presented in this paper, the results of the work by Hosseini-Hashemi et al. [86] and by Zhao and Liew [87] represent other proofs of the validity and the accuracy of the present procedure. As shown, the exact results by Hosseini-Hashemi et al. [86] and the numerical results by Zhao and Liew [84] are in good agreement with those reported by Tornabene [65] and by
FC laminated composite shell resting on an elastic foundation acting on the bottom surface. Also for these cases, the effect of the initial curvature is considered by comparing the present General Shell Theory (GST) and the Reissner-Mindlin (RM) theory. Thus, as regarding the influence of the initial curvature, it is worth noting that the difference between the two theories considered is low for all the laminated composite doubly-curved structures analyzed. Finally, in Figures 6 and 7, there are reported the first six mode shapes for some of the structures considered above. In particular, for the complete shells of revolution there are some symmetrical mode shapes due to the symmetry of the problem considered in 3D space. In these cases, the symmetrical mode shapes are summarized in one figure. The mode shapes of all the structures have been evaluated by the authors. By using the authors’ MATLAB code, these mode shapes have been reconstructed in three-dimensional view by means of considering the displacement field (17) after solving the eigenvalue problem (43). In addition, Hosseini-Hashemi et al. [86] (see table 3) and Zhao and Liew [87] (see Table 6) have compared their results, obtained with a semi analytical method and produced by a meshless method, with those results presented in the articles by Tornabene [65] and by Tornabene et al. [69], respectively. Since the code used to obtain the previous results by Tornabene [65] and Tornabene et al. [69] is similar to the code used to obtain all the results presented in this paper, the results of the work by Hosseini-Hashemi et al. [86] and by Zhao and Liew [87] represent other proofs of the validity and the accuracy of the present procedure. As shown, the exact results by Hosseini-Hashemi et al. [86] and the numerical results by Zhao and Liew [84] are in good agreement with those reported by Tornabene [65] and by
Table 5. First ten frequencies for a 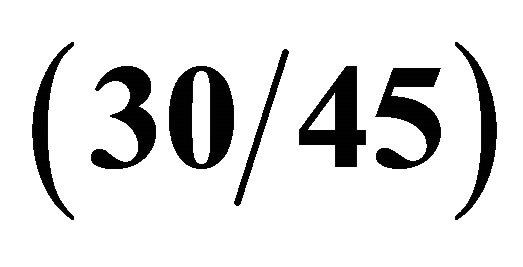 CC shell resting on Winkler-Pasternak elastic foundation.
CC shell resting on Winkler-Pasternak elastic foundation.


*Control points and weights of the Bézier curve: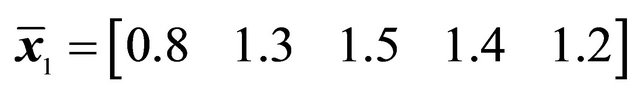 ,
, 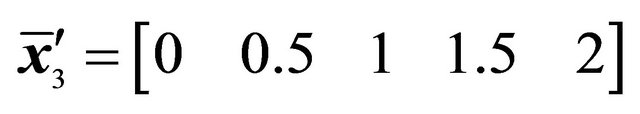 ,
, 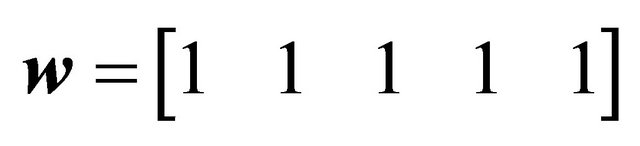 , Geometric characteristics:
, Geometric characteristics: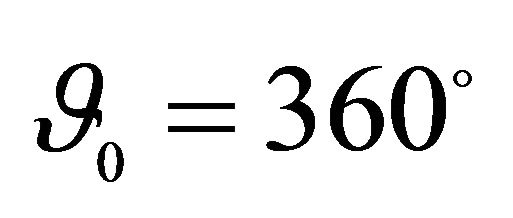 ,
, 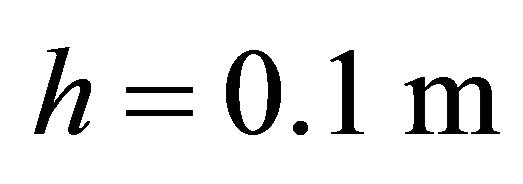 ,
, 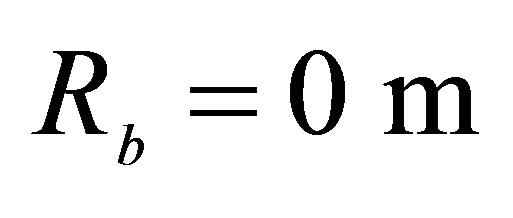 , Orthotropic material:
, Orthotropic material: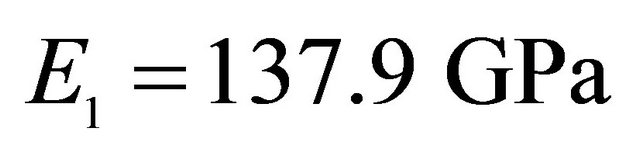 ,
, 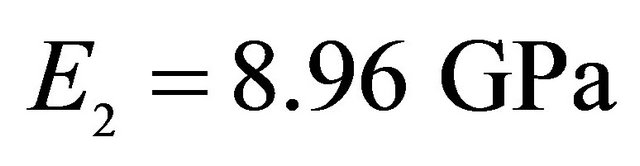 ,
, 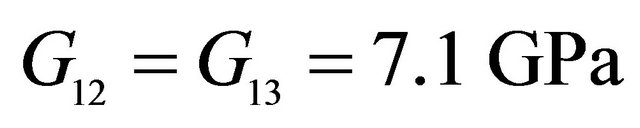 ,
, 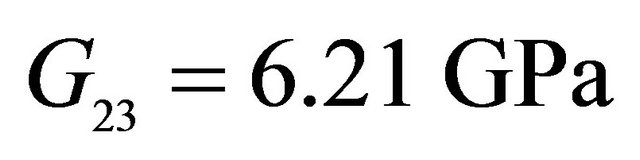 ,
, 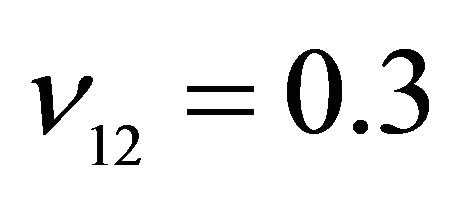 ,
,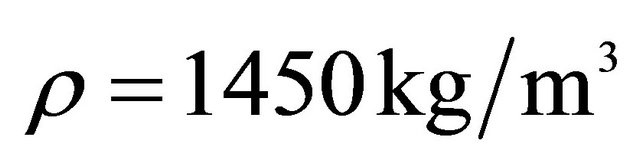 .
.
Table 6. First ten frequencies for a  CCCC panel resting on Winkler-Pasternak elastic foundation.
CCCC panel resting on Winkler-Pasternak elastic foundation.


*Control points and weights of the Bézier curve: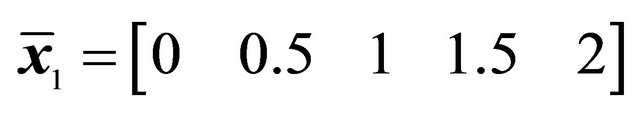 ,
, 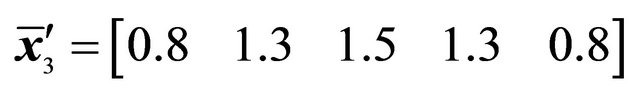 ,
, 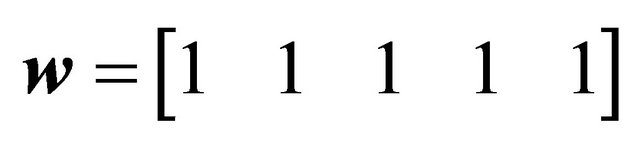 , Geometric characteristics:
, Geometric characteristics: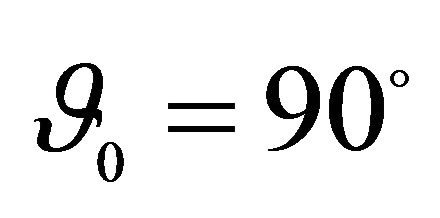 ,
, 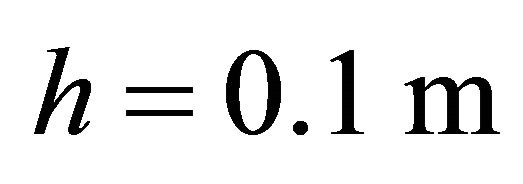 ,
, 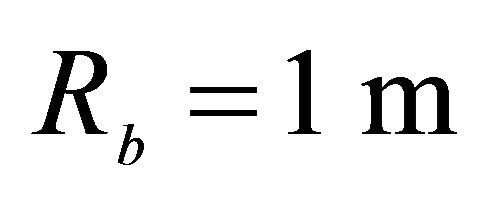 , Orthotropic material:
, Orthotropic material: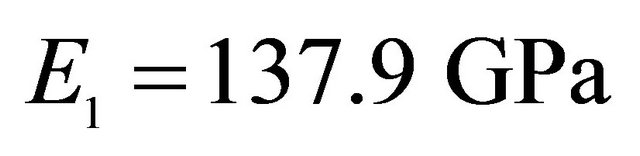 ,
, 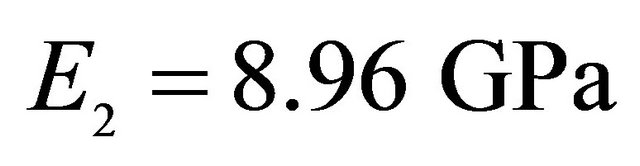 ,
, 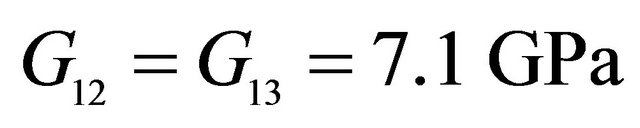 ,
, 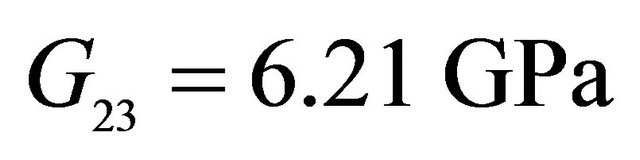 ,
, 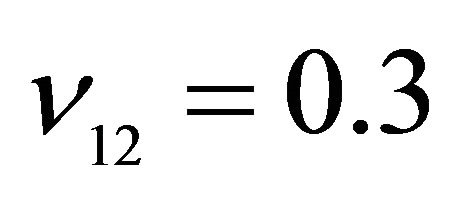 ,
,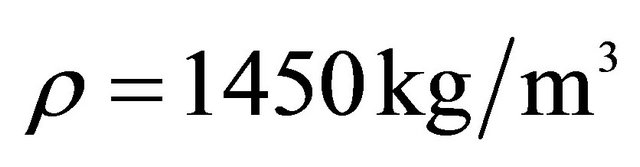 .
.
Table 7. First ten frequencies for a 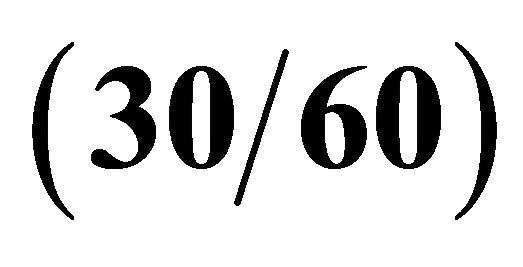 FC shell resting on Winkler-Pasternak elastic foundation.
FC shell resting on Winkler-Pasternak elastic foundation.


*Control points and weights of the Bézier curve: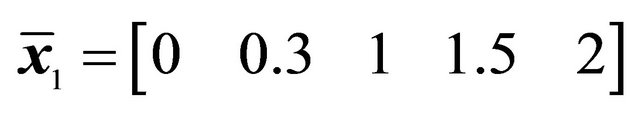 ,
, 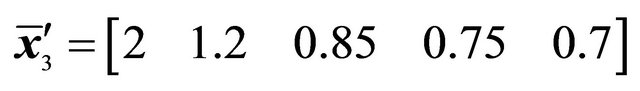 ,
, 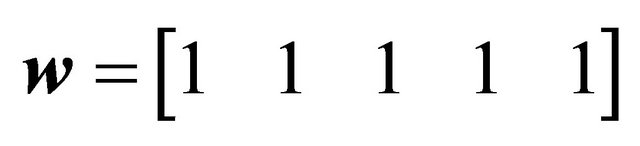 , Geometric characteristics:
, Geometric characteristics: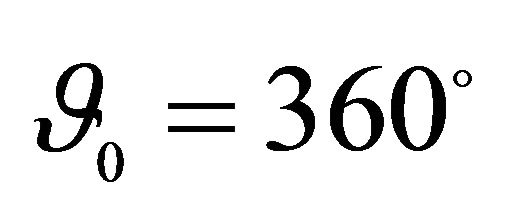 ,
, 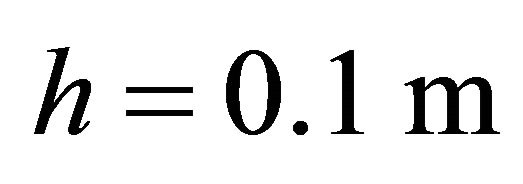 ,
, 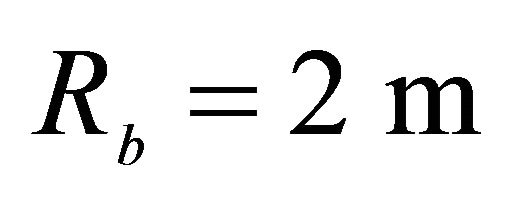 , Orthotropic material:
, Orthotropic material: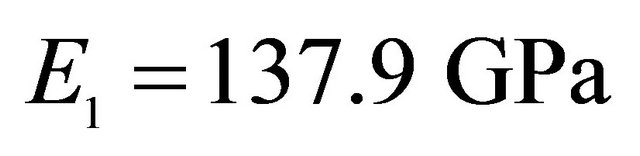 ,
, 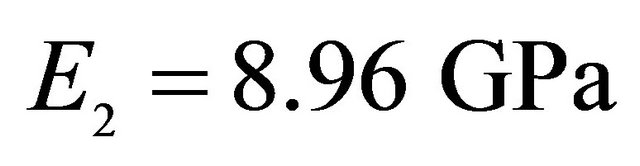 ,
, 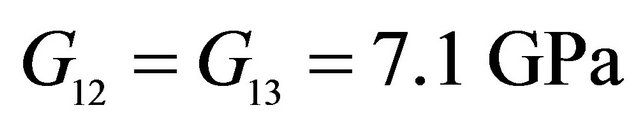 ,
,  ,
, 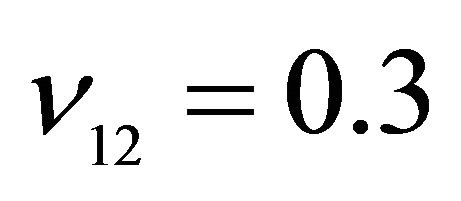 ,
,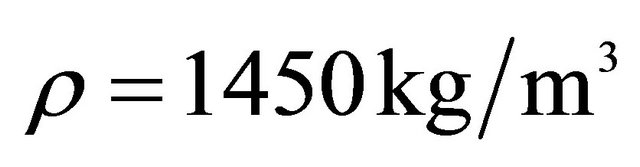 .
.

Figure 6. Mode shapes for the CC shell of Table 5.

Figure 7. Mode shapes for the FC shell of Table 7.
Tornabene et al. [69], respectively. In both cases the discrepancy between results obtained is closely zero.
5. Conclusion
The static and free vibration analyses of laminated doubly-curved shells and panels of revolution resting on Winkler-Pasternak elastic foundations have been presented using the GDQ method. All the effects of the foundation, except the damping, are separately introduced.
New results are presented in order to investigate the effects of the Winkler modulus, the Pasternak modulus and the inertia of the elastic foundation on the behavior of laminated shells of revolution. Simple Rational Bézier curves are used to mathematically describe the shape of the curved shell. Various lamination schemes with different layers have been considered. A general FSDT shell theory has been obtained considering the curvature effect. The fundamental equilibrium equations have been discretized with the GDQ method giving a standard linear problem for the static analysis and a standard linear eigenvalue problem for the dynamic analysis. Numerical solutions have been compared with the ones obtained using commercial programs. The comparisons conducted with FEM codes confirm how the GDQ simple numerical method provides accurate and computationally low cost results for all the structures considered. Furthermore, discretizing and programming procedures are quite easy. The GDQ results show to be precise and reliable. The numerical tests demonstrate and confirm the favorable precision of the Generalized Differential Quadrature Method.
6. Acknowledgements
This research was partially supported by the Italian Ministry for University and Scientific, Technological Research MIUR.
Appendix
The engineering elastic stiffnesses 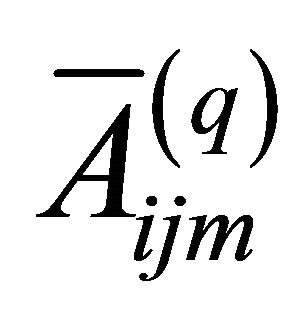 which depend on curvatures for a doubly-curved shell of revolution are defined as it follows:
which depend on curvatures for a doubly-curved shell of revolution are defined as it follows:
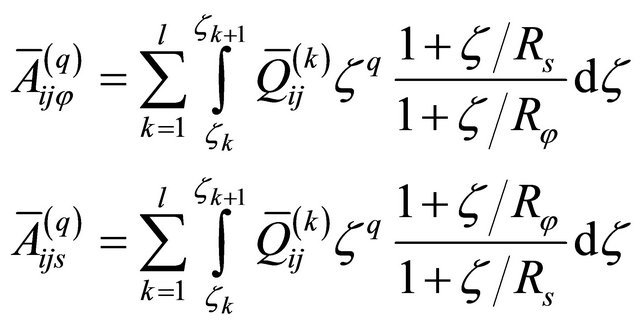 (44)
(44)
Using the Taylor geometric series expansion [7,16-1885], it is possible to introduce the following approximations:
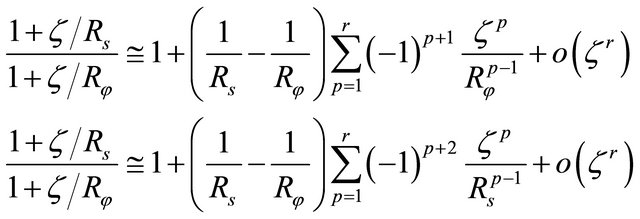 (45)
(45)
where 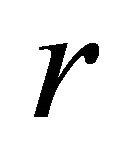 is the maximum order of the series expansions. By neglecting the series terms (45) with order higher than
is the maximum order of the series expansions. By neglecting the series terms (45) with order higher than 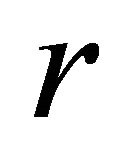 and by introducing the relations (45) into the integrals (44), it is obtained:
and by introducing the relations (45) into the integrals (44), it is obtained:
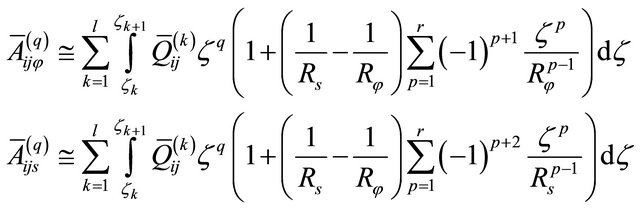 (46)
(46)
Thus, the engineering elastic stiffnesses 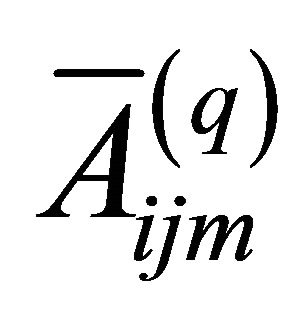 can be evaluated in the following manner:
can be evaluated in the following manner:
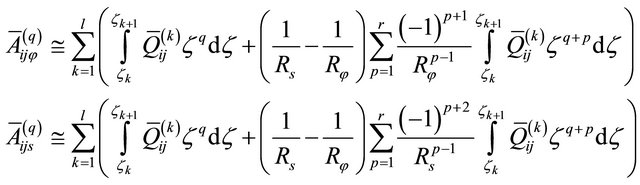 (47)
(47)
The same results can be exactly obtained using the expressions proposed by Qatu [16], by approximating the logarithmic function using a Taylor series expansion. Furthermore, the relations (47) can be defined in the form:
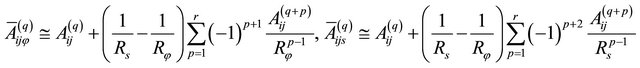 (48)
(48)
where:
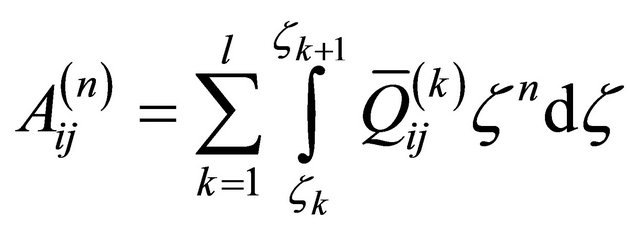 (49)
(49)
Finally, the exact integration of the expressions (47) assume the following aspect:
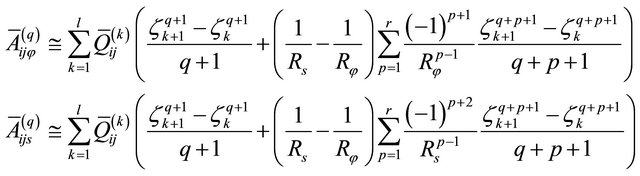 (50)
(50)
whenever the reduced elastic constants 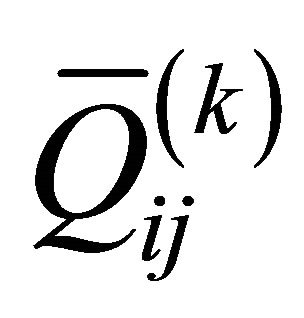 do not depend on
do not depend on  co-ordinate. The engineering elastic stiffness
co-ordinate. The engineering elastic stiffness 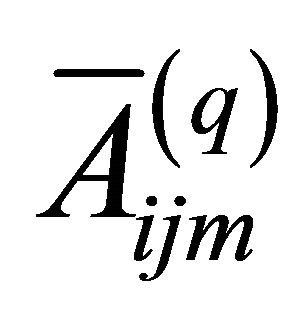 definitions proposed in the present work represent a generalization of the ones proposed in [7,16-18, 77-79,85].
definitions proposed in the present work represent a generalization of the ones proposed in [7,16-18, 77-79,85].
NOTES