1. Introduction
In [1], Levinthal pointed out that assuming a protein folds by randomly searching its native structure it will need time longer than the age of the universe to achieve its native structure. Based on this contradiction, he then concluded that the natural protein folding must be cause-based, that is, the native structure has the (local) minimum value of the Gibbs free energy. Because of too involved in the random thinking of target-based mentality, many people would not understand the proof by contradiction of Levinthal’s mathematical style argument. Instead, they felt that there exists a Levinthal’s paradox that Levinthal never raised. In [2] Ben-Naim dismissed the so called Levinthal’s paradox.
But Ben-Naim invents a new “pitfall”: “This misinterpretation (of thermodynamic hypothesis) has inspired many scientists to search for a global minimum in the Gibbs energy as a function of the conformation of the protein, sometimes referred to as the Gibbs energy landscape. Such a minimum in the Gibbs energy is different from the minimum required by the Second Law of Thermodynamics” [3].
Trying to answer the so called Levinthal’s paradox in [4] Ben-Naim gives the following inference:
“The following two statements are true:
a) The native stable structure of the protein must be at a minimum of the GEL (Gibbs Energy Landscape).
b) Upon releasing a constraint within the system, specified by the variables: T, P N, the Gibbs energy of the system will reach a single absolute minimum”.
Ben-Naim’s conclusion is: “From the two true statements a) and b), people have concluded that the stable state of the protein must be in a global minimum in the GEL. Unfortunately, this conclusion is invalid... The reason so many people fell into this pitfall is that in making statements a) and b), we have not specified the variables with respect to which the Gibbs energy has a minimum”.
Here Ben-Naim implies that conformation of a protein should not be the variable of the Gibbs energy. To answer the question of what is the variable in the Gibbs energy Ben-Naim states in [4]: “For a system characterized by the variables T, P and N”, (respectively the temperature, pressure, and the number of particles) “we can write the Gibbs energy function of the system as . If we start with a system having one particle at a fixed position, say
. If we start with a system having one particle at a fixed position, say , then releasing the constraint on R, but keeping T, P, and N fixed, the system’s Gibbs energy will always decrease by the amount:
, then releasing the constraint on R, but keeping T, P, and N fixed, the system’s Gibbs energy will always decrease by the amount:
 ”.
”.
So Ben-Naim confirms here that the variable of the Gibbs energy is not conformation R. In [4], Ben-Naim continues to state the variable should be probability distributions P of the conformations: “Note again that  is not a monotonic decreasing function of R, and that there exists no value of R, for which G is minimal. Instead, the functional
is not a monotonic decreasing function of R, and that there exists no value of R, for which G is minimal. Instead, the functional  has a single minimum with respect to all possible distributions
has a single minimum with respect to all possible distributions . The distribution
. The distribution , for which G is minimal, is given in Equation (1)”. Ben-Naim’s Equation (1) in [4] is as follows:
, for which G is minimal, is given in Equation (1)”. Ben-Naim’s Equation (1) in [4] is as follows:
 (1)
(1)
Unfortunately, Ben-Naim’s solution of the single minimum (maximum) distribution  at equilibrium is wrong, either for the Gibbs energy functional
at equilibrium is wrong, either for the Gibbs energy functional  or for the entropy function
or for the entropy function  in [4]. Because in physiological environment, almost all proteins are in the native structure, i.e., the native structure has much larger opportunity to appear than any other conformation.
in [4]. Because in physiological environment, almost all proteins are in the native structure, i.e., the native structure has much larger opportunity to appear than any other conformation.
But even someone can get a correct minimum distribution for Ben-Naim, Ben-Naim’s shifting from statement (a) to statement (b) is still a misleading, or a real pitfall. Because it shifts the study of protein structure to the study of probability distribution of conformations. The two are different problems and answer to one would not automatically solve the other problem. For example, even knowing what is Ben-Naim’s minimum distribution, we still do not known what is the three-dimensional shape of the native structure.
In this article, why Ben-Naim falls into a pitfall is analyzed. We will also demonstrate how to derive Gibbs free energy formula  from quantum statistics to show how to get out of Ben-Naim’s “pitfall”, where we have omitted the environment parameters T and P, since they do not vary in nature protein folding process. Where
from quantum statistics to show how to get out of Ben-Naim’s “pitfall”, where we have omitted the environment parameters T and P, since they do not vary in nature protein folding process. Where  is a conformation of the protein
is a conformation of the protein , equivalent to Ben-Naim’s R, and
, equivalent to Ben-Naim’s R, and  is the atomic center of the atom
is the atomic center of the atom , supposing that the molecule has total M atoms. Denying the existence of such
, supposing that the molecule has total M atoms. Denying the existence of such  (it is equivalent to Ben-Naim’s
(it is equivalent to Ben-Naim’s 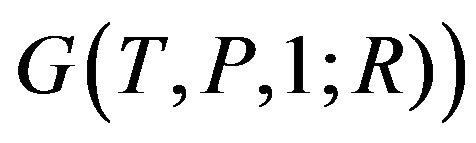 is one of the reasons that Ben-Naim claims “pitfall”. The negative gradient
is one of the reasons that Ben-Naim claims “pitfall”. The negative gradient , is the force that forces the portein to fold. Formulas of
, is the force that forces the portein to fold. Formulas of  are given. The details of the derivation of
are given. The details of the derivation of  is given in Section 7.
is given in Section 7.
2. Where Comes the “Pitfall”
To analysize Ben-Naim’s “pitfall” and look for the reason why there is a “pitfall”, we should recall what is the thermodynamic principle (Anfinsen called it modestly the thermodynamic hypothesis in [5]). Anfinsen stated in [5] clearly that “This hypothesis states that the three-dimensional structure of a native protein in its normal physiological milieu (solvent, pH, ionic strength, presence of other components such as metal ions or prosthetic groups, temperature, and other) is the one in which the Gibbs free energy of the whole system is lowest”; What did Anfinsen mean by the “whole system”? It seems from beginning to present, nobody has really specified it. But all assume that in it there are many conformations of the same protein molecule among other things. Ben-Naim’s molecule number N is no exception. But look at what Anfinsen continued in [5]: “That is, that the native conformation is determined by the totality of interatomic interactions and hence by the amino acid sequence, in a given environment”. Here without any ambiguity the “totality” is “interatomic interactions” of a single protein molecule. Unfortunately, nobody really paid attention to these.
All previous attempts of deriving the Gibbs free energy formula, including Ben-Naim’s, missed the goal of identifying “the three-dimensional structure of a native protein” that Anfinsen had emphasized in above quotation. By their derivation, the whole system consists of  conformations of the same protein molecule, each is only a point in the
conformations of the same protein molecule, each is only a point in the  Euclidean space, supposing that the protein has M atoms. Each micro state of the system, the N points in
Euclidean space, supposing that the protein has M atoms. Each micro state of the system, the N points in , is structureless if we consider the three-dimensional conformation. In this kind of treatment, statistical mechanics cannot tell us anything about “the three-dimensional conformation of a native protein”. Once realized this, one should stop using such kind of systems and start to look for systems that can answer the problem of what is the three-dimensional shape of the native structure.
, is structureless if we consider the three-dimensional conformation. In this kind of treatment, statistical mechanics cannot tell us anything about “the three-dimensional conformation of a native protein”. Once realized this, one should stop using such kind of systems and start to look for systems that can answer the problem of what is the three-dimensional shape of the native structure.
But many just followed the standard setting of statistical mechanics that successfully treated objects such as ideal gas. Instead of telling “the three-dimensional conformation of a native protein”, they shift the problem to that what is the share of the native structure in the probability distribution of conformations. This problem is also interesting and important, but it is a different problem, and as afore mentioned, its resolution tells us nothing about “the three-dimensional conformation of a native protein”. One has to be careful when making inferences between these two different problems. BenNaim’s “pitfall” comes exactly from the misplaced inference, i.e., even knowing what is the correct “minimum distribution ” (Ben-Naim’s is wrong) would not help us to know what is “the three-dimensional conformation of a native protein”, not even one iota.
” (Ben-Naim’s is wrong) would not help us to know what is “the three-dimensional conformation of a native protein”, not even one iota.
Our understanding of the thermodynamic principle is that under the physiological environment, for each conformation  of the peptide chain of the protein molecule
of the peptide chain of the protein molecule  there is a Gibbs free energy
there is a Gibbs free energy . The native structure
. The native structure  has the minimum value of this Gibbs free energy function
has the minimum value of this Gibbs free energy function . The only uncertainty is that
. The only uncertainty is that  might just correspond a local minimum of
might just correspond a local minimum of , as asserted by Levinthal in [1]. Then the initial conformation
, as asserted by Levinthal in [1]. Then the initial conformation  becomes important, because it will determine which local minimum conformation is the native structure
becomes important, because it will determine which local minimum conformation is the native structure .
.
But, to answer the question of what is “the three dimensional conformation of a native protein”? as Anfinsen emphasized, we have to make the transition of conformations in  to conformations in
to conformations in . Based on the three-dimensional geometry of each conformation
. Based on the three-dimensional geometry of each conformation , a thermodynamic system
, a thermodynamic system  should be established, in which among other particles, contain exactly only one protein molecule with the conformation
should be established, in which among other particles, contain exactly only one protein molecule with the conformation . Then one can apply statistical mechanics, classical or quantum, to get the Gibbs free energy of the system
. Then one can apply statistical mechanics, classical or quantum, to get the Gibbs free energy of the system , denoted as
, denoted as .
.
Kinetically, in the physiological environment, an individual protein molecule takes an initial conformation  with a Gibbs free energy
with a Gibbs free energy . With the totality of interatomic interactions of the protein molecule, (we have to add that plus the interaction with its immediate environment), the conformation changes to a series conformations
. With the totality of interatomic interactions of the protein molecule, (we have to add that plus the interaction with its immediate environment), the conformation changes to a series conformations , with Gibbs free energy
, with Gibbs free energy . At last the conformation changes to the native structure
. At last the conformation changes to the native structure  with
with . The “whole” system is the series of systems
. The “whole” system is the series of systems  in (time) series. Searching the native structure
in (time) series. Searching the native structure  then becomes the mathematical problem of solving the minimization problem
then becomes the mathematical problem of solving the minimization problem
 (1)
(1)
The solution of (1) will not only tell us what is the value  (which is not important) but also will tell us what is
(which is not important) but also will tell us what is  (which is the most important). This is one way to answer the question that what is “the three dimensional conformation of a native protein”, i.e., making protein structure prediction.
(which is the most important). This is one way to answer the question that what is “the three dimensional conformation of a native protein”, i.e., making protein structure prediction.
So if we want to resolve the protein folding problem (PFP), for any individual conformation  we should create a tailored thermodynamic system
we should create a tailored thermodynamic system  and derive from it the Gibbs free energy formula
and derive from it the Gibbs free energy formula . Given a native protein’s amino acid sequence, searching for global minimum of
. Given a native protein’s amino acid sequence, searching for global minimum of  is truly following the thermodynamic hypothesis as Anfinsen stated it. Unable to derive such
is truly following the thermodynamic hypothesis as Anfinsen stated it. Unable to derive such  should not be labeled as “misinterpretation of the (thermodynamic) hypothesis” [3]. Lacking of Gibbs free energy function
should not be labeled as “misinterpretation of the (thermodynamic) hypothesis” [3]. Lacking of Gibbs free energy function  explains the question in [4]: “why an answer to this problem (PFP) has been elusive for so long”. The fact that many, including Ben-Naim, in trying to establishing
explains the question in [4]: “why an answer to this problem (PFP) has been elusive for so long”. The fact that many, including Ben-Naim, in trying to establishing  have shifted the variable of
have shifted the variable of  from
from , the conformation, to
, the conformation, to , the probability distribution of
, the probability distribution of  s, partially explains that why for so long such formula
s, partially explains that why for so long such formula  has not been discovered. In particular, one common point of all previous theoretical treatment of protein folding is setting the thermodynamic system contains
has not been discovered. In particular, one common point of all previous theoretical treatment of protein folding is setting the thermodynamic system contains  copies of the same protein molecule, for example [6], thus failed to obtain
copies of the same protein molecule, for example [6], thus failed to obtain .
.
On the other hand, since 1990’s many techniques for probing individual molecules were developed and experimentally observing and testing single molecule is currently a common practice, see [7,8] for example. Theory anyway should not lagged too far behind experiment in single molecule protein folding study.
3. Thermodynamic System  and the Gibbs Free Energy Formula
and the Gibbs Free Energy Formula 
3.1. The Systems
The thermodynamic system  occupies a region in
occupies a region in . Given
. Given , how to put it into a space region
, how to put it into a space region ? And actually, what is
? And actually, what is ? To resolve this we have to use
? To resolve this we have to use ’s three dimensional structure. Assume that each atom has the shape of a ball with van der Wals radius
’s three dimensional structure. Assume that each atom has the shape of a ball with van der Wals radius ,
,  , the three dimensional structure of
, the three dimensional structure of  is
is . The
. The  is the real space or behavior space while the
is the real space or behavior space while the  is only the control space of the protein conformation, [9].
is only the control space of the protein conformation, [9].
To establish  we need some geometric preparation, although it may sounds too mathematical, it is no surprise at all. In fact, Anfinsen stated as early as in 1973 that “biological function appears to be more a correlate of macromolecular geometry than of chemical detail” [5]. Unfortunately, so far, nobody has taken it seriously.
we need some geometric preparation, although it may sounds too mathematical, it is no surprise at all. In fact, Anfinsen stated as early as in 1973 that “biological function appears to be more a correlate of macromolecular geometry than of chemical detail” [5]. Unfortunately, so far, nobody has taken it seriously.
Although the shape of each atom in  is well defined by the theory of atoms in molecules [9,10], what concerning us here is the overall shape of the structure
is well defined by the theory of atoms in molecules [9,10], what concerning us here is the overall shape of the structure . The cutoff of electron density
. The cutoff of electron density  au [9,10], gives the overall shape of a molecular structure that is just like
au [9,10], gives the overall shape of a molecular structure that is just like , a bunch of overlapping balls. Moreover, the boundary of the
, a bunch of overlapping balls. Moreover, the boundary of the  au cut off is almost the same as the molecular surface
au cut off is almost the same as the molecular surface  (Figure 1) which was defined by Richards in 1977 [11] and was shown to be a more suitable boundary surface of
(Figure 1) which was defined by Richards in 1977 [11] and was shown to be a more suitable boundary surface of  than other surfaces in 1992 and 1993 [12,13].
than other surfaces in 1992 and 1993 [12,13].
In mathematics, for any closed surface (compact and connected) , there are a bounded domain
, there are a bounded domain  and a un-bounded domain
and a un-bounded domain  such that
such that
 (2)
(2)
Let  be the diameter of a water molecule and
be the diameter of a water molecule and  be the molecular surface of
be the molecular surface of  with the probe
with the probe

Figure 1. Two dimensional presenting of molecular surface [11] and solvent accessible surface [14]. This figure was originally in [15].
radius . If
. If  is connected, then we can use
is connected, then we can use  in (2). If
in (2). If  has multiple connected components
has multiple connected components ,
,  , such that
, such that  is the largest component, i.e., all other components of
is the largest component, i.e., all other components of  are contained in
are contained in . Then denote
. Then denote  and
and . Thus, we always have
. Thus, we always have
 (3)
(3)
Let  be the distance from a point
be the distance from a point  to a subset
to a subset . Define
. Define
 (4)
(4)
as our thermodynamic system. While
 (5)
(5)
is the first hydration shell surrounding .
.
To be simple, we only consider single peptide chain, self-folding globular proteins here. Hence in the system , except
, except , there are only water molecules and electrons. We have
, there are only water molecules and electrons. We have  and all nuclear centers of water molecules in
and all nuclear centers of water molecules in  are contained in
are contained in . Moreover, since
. Moreover, since  is bounded, it has a finite volume
is bounded, it has a finite volume .
.
The thermodynamic system  will be an open system, i.e., electrons and water molecules can enter and leave
will be an open system, i.e., electrons and water molecules can enter and leave . Therefore, the numbers
. Therefore, the numbers  and
and , of water molecules and electronics in
, of water molecules and electronics in  are variables. According Anfinsen [5], the protein folding process is after the peptide chain synthesis. Therefore, part of the totality of the “interatomic interactions”, as emphasized by Anfinsen in [5], has already contributed to form correct chemical bonds. In the folding process, “chemical details” may be represented by the forming of intramolecular hydrogen bonds and the interactions with the immediate environment, in our case, the solvent consisting of water molecules.
are variables. According Anfinsen [5], the protein folding process is after the peptide chain synthesis. Therefore, part of the totality of the “interatomic interactions”, as emphasized by Anfinsen in [5], has already contributed to form correct chemical bonds. In the folding process, “chemical details” may be represented by the forming of intramolecular hydrogen bonds and the interactions with the immediate environment, in our case, the solvent consisting of water molecules.
Ben-Naim claims that “in the author’s opinion, the main hindrance to finding a solution to the protein folding problem has been the adherence to the hydrophobic (HOO) dogma, which states that various HOO effects (both solvation and interaction) are the dominant forces in protein folding” and “an exhaustive analysis of all the solvent induced effects on protein folding reveals that the hydrophilic (HOI) effects are much more important than the corresponding HOO effects” [2].
In [15] a simulation of enlarging the hydrophobic core alone, whose forming is considered the main effect of HOO, not only produced secondrary structures, but also produced the intra-molecular hydrogen bonds. This result shows that HOO should not be dismissed so simply.
But no matter the driving force of protein folding is HOO or HOI, a common essence for them is that in a protein there are many different moieties or atom groups with different levels of ability of forming hydrogen bonds (hydrophobic levels). Simply classifying amino acids as hydrophobic or hydrophilic is an over simplification [16]. In fact, since each atom belongs to a particular moiety or atom group, it can be assigned a hydrophobic level as the level of the moiety or atom group. Suppose we classify the atoms into  hydrophobic levels
hydrophobic levels ,
,  , such that
, such that . For example, in [16] there are
. For example, in [16] there are  classes, C, O/N, O–, N+, S. If a hydrogen atom is bonded with an atom in
classes, C, O/N, O–, N+, S. If a hydrogen atom is bonded with an atom in , we will put it in
, we will put it in .
.
Let  be the subset such that
be the subset such that  if and only if
if and only if . Define
. Define  and as shown in Figure 2,
and as shown in Figure 2,
 (6)
(6)
Let  be the volume of
be the volume of , then
, then
 (7)
(7)
Define the hydrophobicity subsurface ,
,  , as
, as
 (8)
(8)
Let  be the area of a surface
be the area of a surface , then
, then
 (9)
(9)

Figure 2. Note that RXi generally are not connected, i.e., having more than one block.
3.2. The Formulas
In our open thermodynamic system, there will be  water molecules in
water molecules in , and
, and  electrons in
electrons in , thus we will denote the variable
, thus we will denote the variable  as a vector
as a vector
 .
.
After statistical treatment, the mean number of  and
and  will be denoted as
will be denoted as ,
,  ,
, . Each water molecule in
. Each water molecule in  will contact
will contact . The chemical potential reflecting the contacting energy will be denoted as
. The chemical potential reflecting the contacting energy will be denoted as . Similarly, the energy for an electron kept in
. Similarly, the energy for an electron kept in  will be the chemical potential
will be the chemical potential . With these preparation, arguing in quantum statistics via the grand canonic ensemble we derive the Gibbs free energy of protein folding
. With these preparation, arguing in quantum statistics via the grand canonic ensemble we derive the Gibbs free energy of protein folding  as follows (see Section 7 for the detailed derivation, also see [17,18] for further discussions):
as follows (see Section 7 for the detailed derivation, also see [17,18] for further discussions):
 (10)
(10)
Note that in the folding process, each intermediate structure  is not in a stationary state, it is rather a system of quasi-equilibrium states of the folding. So that it is not the case that
is not in a stationary state, it is rather a system of quasi-equilibrium states of the folding. So that it is not the case that , as in equilibrium state. Rather, the chemical potentials will be constants during the folding, as the environment is kept unchanged.
, as in equilibrium state. Rather, the chemical potentials will be constants during the folding, as the environment is kept unchanged.
Formula (10) is not easy to calculate, we can convert it into a geometric form that is not only calculable but also coincident to a mathematically derived formula appeared in [15,19].
Since every water molecule in  has contact with the surface
has contact with the surface  and the curvature of
and the curvature of  is uniformly bounded,
is uniformly bounded,  is proportional to the area
is proportional to the area . That is, there are
. That is, there are , independent of
, independent of , such that
, such that
 (11)
(11)
Similarly, there will be a , independent of
, independent of , such that
, such that .
.
By the definition of  and
and , we have roughly
, we have roughly . Thus
. Thus
 (12)
(12)
Substitute (11) and (12) into (10), we get
 (13)
(13)
This Gibbs free energy function  really should be written as
really should be written as , where
, where  is environment, its parameters including the temperature
is environment, its parameters including the temperature 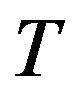 and pressure
and pressure  which will affect the values of chemical potential
which will affect the values of chemical potential  and
and . Since protein folding is in a fixed physiological environment, we can omit
. Since protein folding is in a fixed physiological environment, we can omit  in this stage.
in this stage.
It should be emphasized here that since we assumed that the proteins are single peptide chain, self-folding globular proteinsins, the first hydration of  contains only water molecules and electrons, no presence of other components at all, this Gibbs free energy function
contains only water molecules and electrons, no presence of other components at all, this Gibbs free energy function  should be only suitable to these proteins. For other kinds of proteins, the presence of other components such as chaperonins must be considered in the thermodynamic system
should be only suitable to these proteins. For other kinds of proteins, the presence of other components such as chaperonins must be considered in the thermodynamic system . Then, the geometry of
. Then, the geometry of  will become more complicated.
will become more complicated.
4. Applying and Testing the Thermodynamic Hypothesis
Anfisen had shown that the protein folding is a spantenously process [5], thus the thermodynamic hypothesis should be treated as thermodynamic principle. A direct application of it, also a real test of it, is the ab initio prediction of a protein’s native structure as in (1). However, without control of overlapping of the balls , we may get a single ball with all other balls collapsed in it as a minimum structure, a disaster for a prediction. The pairwise potentials used for force fields will prevent the collapsing happen. Why the pairwise potential energy among atoms of the protein
, we may get a single ball with all other balls collapsed in it as a minimum structure, a disaster for a prediction. The pairwise potentials used for force fields will prevent the collapsing happen. Why the pairwise potential energy among atoms of the protein  does not show in formulae (10) and (13)? The reason is that according to Anfinsen [5], protein folding is after the synthesis of the whole peptide chain. So that during the folding process all covalent bonds in the main chain and each side chain are already formed and non-bonding atoms keep a certain distance from each other. That is, the potential energy has already played its role during the synthesis of the peptide chain. This reality forces us to restrict what
does not show in formulae (10) and (13)? The reason is that according to Anfinsen [5], protein folding is after the synthesis of the whole peptide chain. So that during the folding process all covalent bonds in the main chain and each side chain are already formed and non-bonding atoms keep a certain distance from each other. That is, the potential energy has already played its role during the synthesis of the peptide chain. This reality forces us to restrict what  can be treated as a conformation, i.e., a conformation should satisfy the steric conditions below.
can be treated as a conformation, i.e., a conformation should satisfy the steric conditions below.
There are ,
,  such that for nuclear centers
such that for nuclear centers  and
and  in
in ,
,
 (14)
(14)
We will denote all conformations satisfying (14) as . Then the minimization will become:
. Then the minimization will become:
 (15)
(15)
or, at least, within ,
,  corresponds to a local minimum of
corresponds to a local minimum of .
.
With the steric conditions we avoided the collapsing problem. But the steric conditions turn the minimization problem (1) into a constrained minimization problem (15). Mathematically the latter is much more difficult to solve. To avoid the constraint in minimization for nonbonding atoms, we can use the van der Waals force to modify the formula as:

(16)
where  is the corresponding energy and
is the corresponding energy and  and
and  the ideal distance between the atoms
the ideal distance between the atoms  and
and . Before using
. Before using  to eliminate the constraint of
to eliminate the constraint of , we take a more convenient coordinate of the conformation
, we take a more convenient coordinate of the conformation . We require that all bond lengths and angles (denoted as one angle-length pattern) are kept as obtained from a conformation
. We require that all bond lengths and angles (denoted as one angle-length pattern) are kept as obtained from a conformation  and from
and from  calculate the values of all rotatable dihedral angles
calculate the values of all rotatable dihedral angles  (including all the main chain
(including all the main chain ,
,  s). In fact, new conformations obtained by changing
s). In fact, new conformations obtained by changing  will keep the same angle-length pattern and all conformations with the same angle-length pattern as
will keep the same angle-length pattern and all conformations with the same angle-length pattern as  are obtained by choose suitable
are obtained by choose suitable  values. The function
values. The function  then can be written as
then can be written as
 (17)
(17)
Let  have the dihedral angles
have the dihedral angles , then the constraint in (15) will be relaxed and we will have a minimization problem without any constraint:
, then the constraint in (15) will be relaxed and we will have a minimization problem without any constraint:
 (18)
(18)
5. The Force That Forces the Protein to Fold
Ben-Naim correctly emphasizes that the protein folding is a cause-based process, “One can imagine that at each stage of the folding process, there are strong solventinduced forces exerted on the various groups along the protein. These forces will force the protein to fold along a narrow range of pathways...” [2], and the folding force actually is the negative of the gradient of the Gibbs free energy function, that is , “we need to know the forces acting on each of the M groups of the protein being at the conformation
, “we need to know the forces acting on each of the M groups of the protein being at the conformation . This force is obtained by taking the gradient of the Gibbs energy with respect to each of the
. This force is obtained by taking the gradient of the Gibbs energy with respect to each of the ” [4].
” [4].
However, with only a “minimum distribution ” Ben-Naim cannot tell what is the garden
” Ben-Naim cannot tell what is the garden . With formula (13), it is easy to write down mathematical formula of
. With formula (13), it is easy to write down mathematical formula of . For example, in the coordinates
. For example, in the coordinates , the folding force is
, the folding force is
 (19)
(19)
5.1. Newton’s Fastest Descending Method
Before giving the formula of , we will point out that if it is calculable, then we can apply the fastest descending method to pursue the minimum value of
, we will point out that if it is calculable, then we can apply the fastest descending method to pursue the minimum value of . That is, starting from a
. That is, starting from a , the immediate next conformation
, the immediate next conformation  will be chosen such that
will be chosen such that
 (20)
(20)
where  is a suitable step length. When
is a suitable step length. When  is small, it is guaranteed that
is small, it is guaranteed that . Any (local) minimum
. Any (local) minimum  would have that
would have that .
.
5.2. The Formula of 
We will give the analytic formula of  here without mathematical proof. It is:
here without mathematical proof. It is:

(21)
It should be mentioned here that bond in  is rotatable if it is a single bond and if we cut this bond, all nuclear centers in
is rotatable if it is a single bond and if we cut this bond, all nuclear centers in  can be divided into two (nonempty) groups, such that we can fix one group and rotate around the bond axis the other group. Let
can be divided into two (nonempty) groups, such that we can fix one group and rotate around the bond axis the other group. Let  be the outer product in
be the outer product in . Let
. Let  be the bond, then
be the bond, then  will be the rotation axis and
will be the rotation axis and  the rotation vector field, i.e.,
the rotation vector field, i.e.,  if
if  is a rotated nuclear center; and
is a rotated nuclear center; and  if
if  is a fixed nuclear center. Furthermore,
is a fixed nuclear center. Furthermore,
 (22)
(22)
and
 (23)
(23)
where  and
and  are the outer unit normal and the mean curvature of
are the outer unit normal and the mean curvature of ,
,  and
and  the Hausdorff measures of dimensions 2 and 1. Let
the Hausdorff measures of dimensions 2 and 1. Let  be the family of conformations such that
be the family of conformations such that  and
and ,
, . Define
. Define  as
as , and denote
, and denote
 (24)
(24)
Finally, if  is rotated and
is rotated and  is fixed, then
is fixed, then
 (25)
(25)
if  and
and  are both rotated or both fixed, then we have
are both rotated or both fixed, then we have .
.
The integration of above formulae on the molecular surface  are given in [20].
are given in [20].
6. Conclutions
The Ben-Naim’s pitfall of “misinterpretation of thermodynamic hypotheses” is dismissed as a Don Quixote’s windmill by demonstrating the existence of Gibbs free energy formulas (10) and (13), pursuing of them were claimed by Ben-Naim as fallen into a pitfall. The formulae themselves need detailed geometric formulation of the thermodynamic system to present them, is a realization of Anfinsen’s insight that “biological function appears to be more a correlate of macromolecular geometry than of chemical detail” [5]. Contrary to BenNaim’s claims that “In the author’s opinion, the main hinderence to finding a solution to the protein folding problem has been the adherence to the hydrophobic (HOO) dogma” [2], the derivation of (10) and (13) heavily depends on the concept of hydrophobicity.
In Section 7, the quantum statistical derivation of formula (10) is given, the convertion of (10) to (13) is demonstrated in Section 3.2.
Ben-Naim’s minimization at  is analyzed and dismissed because it predicts that at equilibrium every possible conformation
is analyzed and dismissed because it predicts that at equilibrium every possible conformation  will have the same probability to be the structure of a native protein. That is, BenNaim claims that
will have the same probability to be the structure of a native protein. That is, BenNaim claims that  for any conformation
for any conformation . In fact, in the contrary, in the physiological environment the native structure is dominate.
. In fact, in the contrary, in the physiological environment the native structure is dominate.
The reason of why calculable formulas such as (10) and (13) have not appeared so far is discussed, blindly imitating successful classical examples of applying statistical mechanics and ignoring Anfinsen’s insight are two main reasons.
The force that forces the protein to fold is identified as  by general physical law, that Ben-Naim has correctly pointed out. The calculable formula of
by general physical law, that Ben-Naim has correctly pointed out. The calculable formula of  is given.
is given.
7. Derivation of Formula (10)
7.1. The Shrödinger Equation
For any conformation , let
, let  be the nuclear centers of oxygen atoms in water molecules in
be the nuclear centers of oxygen atoms in water molecules in  and
and  be electronic positions of all electrons in
be electronic positions of all electrons in . Then the Hamiltonian for the system
. Then the Hamiltonian for the system  is:
is:
 (26)
(26)
where  is the nuclear mass of atom
is the nuclear mass of atom  in
in ,
,  and
and  the masses of water molecule and electron,
the masses of water molecule and electron,  the Laplacian in corresponding
the Laplacian in corresponding , and V the potential.
, and V the potential.
7.2. The First Step of the Born-Oppenheimer Approximation
Depending on the shape of , for each
, for each ,
,  , the maximum numbers
, the maximum numbers  of water molecules contained in
of water molecules contained in  vary. Theoretically we consider all cases, i.e., there are
vary. Theoretically we consider all cases, i.e., there are  water molecules in
water molecules in ,
, . Let
. Let  and
and  and
and ,
,  , and
, and  denote the nuclear positions of water molecules in
denote the nuclear positions of water molecules in . As well, there will be all possible numbers
. As well, there will be all possible numbers  of electrons in
of electrons in . Let
. Let  denote their nuclear positions. For each fixed
denote their nuclear positions. For each fixed  and
and , the Born-Oppenheimer approximation has the Hamiltonian
, the Born-Oppenheimer approximation has the Hamiltonian

The eigenfunctions ,
,  , comprise an orthonormal basis of
, comprise an orthonormal basis of . Denote their eigenvalues (energy levels) as
. Denote their eigenvalues (energy levels) as , then
, then
 .
.
7.3. Grand Partition Function and Grand Canonic Density Operator
In the following we will use the natotions and definitions in [21, Chapter 10]. Let  be the Bolzmman constant, set
be the Bolzmman constant, set . Since the numbers
. Since the numbers  and
and  vary, we should adopt the grand canonic ensemble. Let
vary, we should adopt the grand canonic ensemble. Let  be the chemical potentials, that is, the Gibbs free energy per water molecule in
be the chemical potentials, that is, the Gibbs free energy per water molecule in . Let
. Let  be electron chemical potential. The grand canonic density operator is ([21, 22])
be electron chemical potential. The grand canonic density operator is ([21, 22])

where the grand partition function is

7.4. The Gibbs Free Energy 
According to [21, p. 273], under the grand canonic ensemble the entropy  of the system
of the system  is
is

(27)
Here we denote  the mean numbers of water molecules in
the mean numbers of water molecules in ,
,  , and
, and  the mean number of electrons in
the mean number of electrons in . The inner energy
. The inner energy  of the system
of the system  is denoted as:
is denoted as:
 .
.
The term  is a state function with variables
is a state function with variables , and
, and , and is called the grand canonic potential ([21, p. 27]) or the thermodynamic potential ([22, p. 33]). By the general thermodynamic equations [22, pp. 5-6]:
, and is called the grand canonic potential ([21, p. 27]) or the thermodynamic potential ([22, p. 33]). By the general thermodynamic equations [22, pp. 5-6]:

we see that
 where
where  is the volume of the thermodynamic system
is the volume of the thermodynamic system . Thus by (27) we obtain the Gibbs free energy
. Thus by (27) we obtain the Gibbs free energy  in (10):
in (10):
