1. Introduction
Let G be a simple connected graph with vertex set V(G) and edge set E(G) so that  and
and . For any vertex
. For any vertex , let deg(v) denote the degree of the vertex v. For vertices u and
, let deg(v) denote the degree of the vertex v. For vertices u and , the distance between u and v is defined as length of the shortest path connecting u and v and is denoted by d(u,v). The eccentricity of a vertex
, the distance between u and v is defined as length of the shortest path connecting u and v and is denoted by d(u,v). The eccentricity of a vertex , denoted by
, denoted by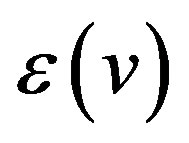 , is the distance between v and a vertex farthest from v i.e.
, is the distance between v and a vertex farthest from v i.e. . The radius
. The radius  and diameter
and diameter  of a graph is the minimum and maximum eccentricity among the vertices of G i.e.
of a graph is the minimum and maximum eccentricity among the vertices of G i.e.

and

respectively. Also the total eccentricity of a graph, denoted by , is the sum of all the eccentricities of G [1] i.e.
, is the sum of all the eccentricities of G [1] i.e.
 .
.
The first and second Zagreb index of a graph were first introduced by Gutman in [2] which are the most known and widely used topological indices, defined as respectively
 ,
,

Recently several Graph invariants based on vertex eccentricities subject to large number of studies. Analogues to Zagreb indices M. Ghorbani et al. [3] and D. Vukičević et al. [4] defined the Zagreb eccentricity indices by replacing degrees by eccentricity of the vertices. Thus the first and second Zagreb eccentricity indices of a graph G are defined as
 ,
,

The lower and upper bounds of n-vertex trees with fixed diameter and matching number and extremal trees with respect to Zagreb eccentricity indices were studied by R. Xing et al. [5] and recently K. C. Das et al. in [6] presented some properties, upper and lower bounds of Zagreb eccentricity indices and also characterize the extremal graphs.
Another useful eccentricity and degree based topological index called eccentric connectivity index was first introduced by Sharma, Goswami and Madan [7] and is defined as

There was a vast research regarding various properties of this topological index [8-10].
The study of determining extremal properties such as upper bounds and lower bounds of some graph invariants were subject to a large number of investigations [11-15]. The aim of this paper is to study similar extremal properties for Zagreb eccentricity indices. In this paper we present some new upper and lower bounds of Zagreb eccentricity indices in terms of number of vertices (n), number of edges (m), radius (r), diameter (d), total eccentricity , the first Zagreb indices (M1(G)), the second Zagreb indices (M2(G)) and the eccentric eccentricity index
, the first Zagreb indices (M1(G)), the second Zagreb indices (M2(G)) and the eccentric eccentricity index .
.
2. Bounds for the First Zagreb Eccentricity Index
We now give some lower and upper bounds of first Zagreb eccentricity index. In [6] Das et al. proved the following upper bound of E1(G).
Theorem 2.1. Let G be a simple connected graph with n vertices and m edges, then

with equality if and only if  or
or  or G is isomorphic to a (n ‒ 1, n ‒ 2)-semiregular graph.
or G is isomorphic to a (n ‒ 1, n ‒ 2)-semiregular graph.
Also, in [5] Xing et al. give the following result.
Theorem 2.2. Let G be a simple connected graph with n vertices and m edges, then

with equality if and only if G all the vertices of G are of same eccentricity.
Also in [6] Das et al. give lower bounds for E1(G) in terms of n and d. Now we prove some new upper and lower bounds of E1(G).
Theorem 2.3. Let G be a simple connected graph with n vertices and m edges, then

with equality if and only if G all the vertices of G are of same eccentricity.
Proof Using the Cauchy-Schwartz inequality, we get

and hence using the definition of total eccentricity index and first Zagreb eccentricity index the desired result follows. Clearly in the above inequality equality holds when all the vertices of G are of same eccentricity.
Theorem 2.4. Let G be a simple connected, then

with equality if and only if .
.
Proof We have, for all ,
,  with equality if an only if
with equality if an only if , where
, where  is the degree distance of the vertex v and is defined as
is the degree distance of the vertex v and is defined as
 .
.
Hence from the definition of first Zagreb eccentricity index, we can write
 (2.1)
(2.1)
Now since  for all
for all , so from (2.1) we get the desired result with equality if and only if
, so from (2.1) we get the desired result with equality if and only if 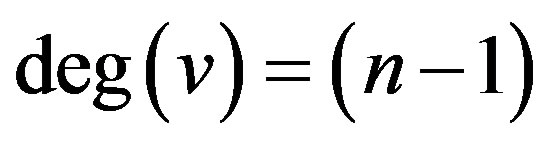 and
and , that is
, that is .
.
Corollary 2.1. Let G be a simple connected graph with n vertices and m edges, then
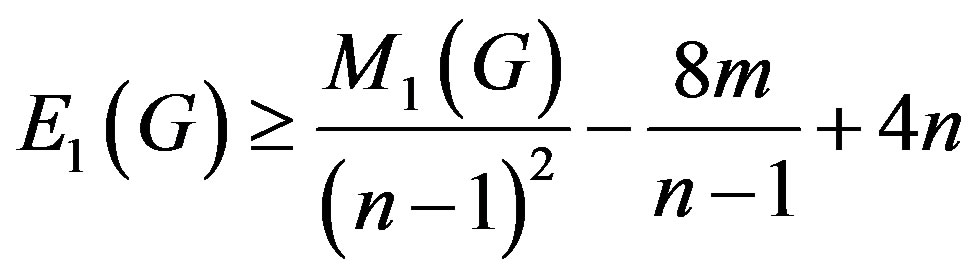
with equality if and only if G is a path of length one.
Proof Again since,  , for all
, for all , with equality if and only if
, with equality if and only if , so from (2.1) we get the desired result. Since the equality (2.1) holds if and only if
, so from (2.1) we get the desired result. Since the equality (2.1) holds if and only if  so the equality holds in this result if and only if G is a path of length one which is the only complete graph as well as complete bipartite graph.
so the equality holds in this result if and only if G is a path of length one which is the only complete graph as well as complete bipartite graph.
Theorem 2.5. Let G be a simple connected graph on n vertices and  be the number of vertices with eccentricity one in G, then
be the number of vertices with eccentricity one in G, then

with equality if and only if , where
, where  is even.
is even.
Proof Since  be the number of vertices with eccentricity one in G, so the remaining
be the number of vertices with eccentricity one in G, so the remaining  vertices are of eccentricity at least two. Let
vertices are of eccentricity at least two. Let  be the set of vertices such that
be the set of vertices such that  for
for .
.
Then from the definition of first Zagreb eccentricity index, we have
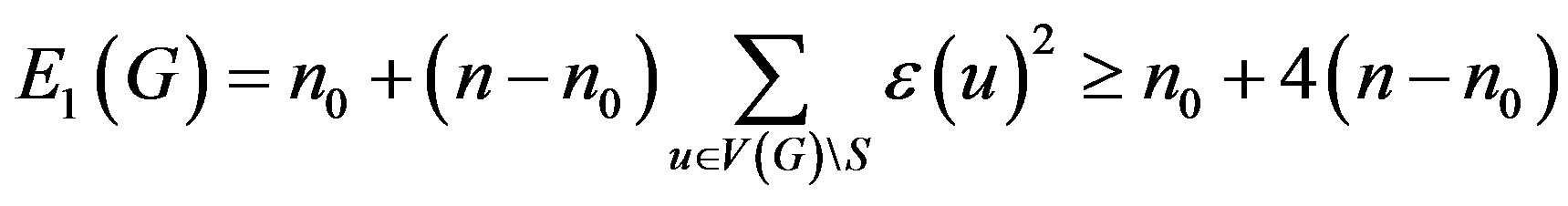
from where the desired result follows. Clearly, in this theorem equality holds if and only if where
where  is even.
is even.
Theorem 2.6. Let G be a simple connected graph with n vertices and m edges, then

with equality if and only if all the vertices of G are of same eccentricity.
Proof To prove this theorem, using the following Diaz-Metcalf inequality, we have, if ai and bi,  are real numbers such that
are real numbers such that  for
for , then
, then
 (2.2)
(2.2)
In the above inequality equality holds if and only if  or
or  for every
for every . By setting
. By setting 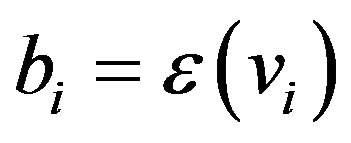 and
and , for
, for , in (2.2) from above inequality we get
, in (2.2) from above inequality we get

Now using the definition of first Zagreb eccentricity index and total eccentricity index we get

Since,  for
for , so we have
, so we have  and
and . Hence the desired result follows from above. Clearly in the above inequality equality holds if and only if all the vertices of G are of same eccentricity.
. Hence the desired result follows from above. Clearly in the above inequality equality holds if and only if all the vertices of G are of same eccentricity.
Theorem 2.7. Let G be a simple connected graph, then

In the above inequality equality holds if and only if all the vertices of G are of same eccentricity.
Proof Let, sum of eccentricities of the vertices adjacent to

so that

from where we get the desired result. Obviously in the above inequality equality holds if and only if all the vertices of G are of same eccentricity.
Theorem 2.8. Let G be a simple connected graph on n vertices and m edges, then

In the above inequality equality holds if and only if all the vertices of G are of same eccentricity.
Proof We will prove this theorem using the following Chebyschev’s inequality: Let  and
and  are real numbers, then
are real numbers, then

with equality holds if and only if
 or
or .
.
Now setting  and
and , for
, for , we get from (2.3)
, we get from (2.3)
 (2.4)
(2.4)
Again since

with equality holding if and only if
 we get from (2.4)
we get from (2.4)
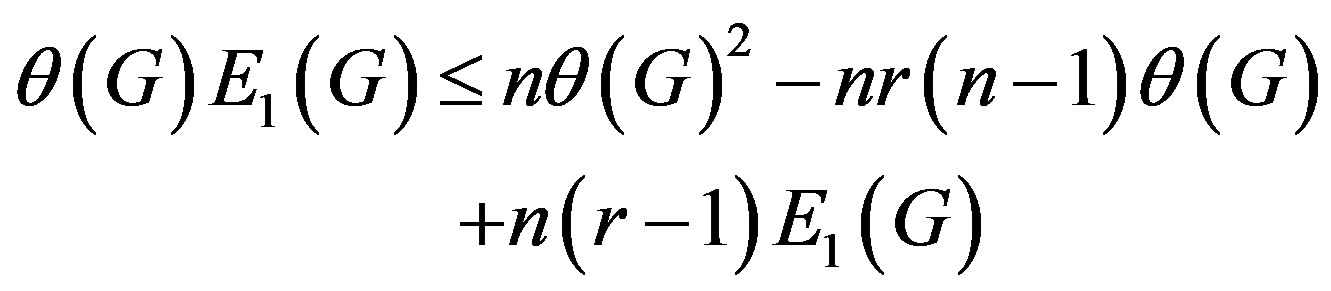
from where we get the desired result. Clearly in this inequality equality holds if and only if all the vertices are of same eccentricity.
Theorem 2.9. Let G be a simple connected graph where all the vertices must not be of equal eccentricity, then

where G consists of a number of vertices with eccentricity d and b number of vertices with eccentricity r. In the above inequality equality holds if and only if eccentricities of the vertices are equal to r + 1, r, d ‒ 1, d.
Proof For any vertex , we have
, we have

with equality holds if and only if  or
or  for
for . Now summing the above inequality for
. Now summing the above inequality for , we get
, we get

So,

from where we get the desired result. In the above inequality equality holds if and only if
 .
.
From the above theorem the following result directly follows.
Corollary 2.2. Let G be a simple connected graph with n vertices and m edges, then

where k is the number of vertices having eccentricity equal to d or r.
3. Bounds for the Second Zagreb Eccentricity Index
In [6] Das et al. give lower bounds for E2(G) in terms of m, d and proved the following upper bound of E1(G).
Theorem 3.1. Let G be a simple connected graph with n vertices and m edges, then
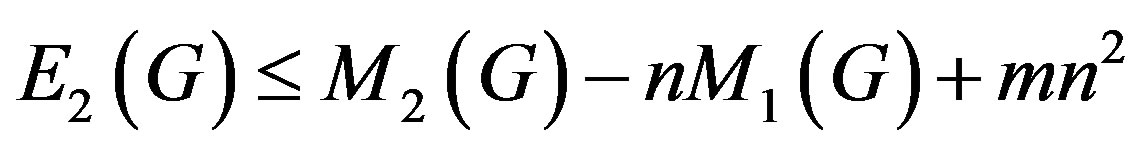
with equality if and only if  or
or  or G is isomorphic to a (n ‒ 1, n ‒ 2)-semiregular graph.
or G is isomorphic to a (n ‒ 1, n ‒ 2)-semiregular graph.
Also, in [5] Xing et al. proved the following result.
Theorem 3.2. Let G be a simple connected graph with n vertices and m edges, then

with equality if and only if G all the vertices of G are of same eccentricity.
Now we prove some new upper and lower bounds of E2(G).
Theorem 3.3. Let G be a simple connected graph with n vertices and m edges, then

with equality if and only if G all the vertices of G are of same eccentricity.
Proof Using the inequality between arithmetic and geometric mean, we get

Now let,  , so that taking natural logarithm on both sides and using Jensen’s inequality, we get
, so that taking natural logarithm on both sides and using Jensen’s inequality, we get

Thus , so that
, so that which is the desired result. In this inequality equality holds if and only if all the vertices of G are of same eccentricity.
which is the desired result. In this inequality equality holds if and only if all the vertices of G are of same eccentricity.
Theorem 3.4. Let G be a simple connected graph, then

where, 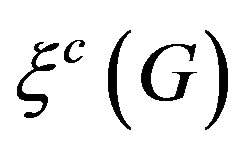 is the eccentric connectivity index of G. In the above inequality equality holds if and only if
is the eccentric connectivity index of G. In the above inequality equality holds if and only if  or
or  for all
for all .
.
Proof Since  for all
for all , we have
, we have . So from the definition of second Zagreb eccentricity index, we can write
. So from the definition of second Zagreb eccentricity index, we can write

Now since
 the desired result follows from above. In the above inequality equality holds if and only if
the desired result follows from above. In the above inequality equality holds if and only if  or
or  for all
for all , for example if and only if
, for example if and only if  or
or .
.
Theorem 3.5. Let G be a simple connected graph with n vertices and m edges, then

with equality if and only if .
.
Proof Since, for all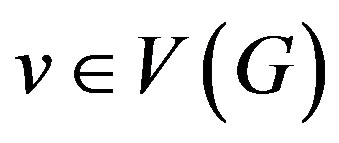 ,
,  , with equality if an only if
, with equality if an only if , like Theorem 2.4, using definition of second Zagreb eccentricity index the desired result follows.
, like Theorem 2.4, using definition of second Zagreb eccentricity index the desired result follows.
Corollary 3.1. Let G be a simple connected graph with n vertices and m edges, then

with equality if and only if G is a path of length one.
Proof Since,  for all
for all
 , with equality if and only if
, with equality if and only if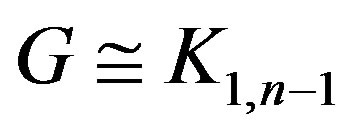 , like Corollary 2.1, from the Theorem 3.5 we have
, like Corollary 2.1, from the Theorem 3.5 we have

from where we get the desired result. Like Corollary 2.1, in this inequality equality holds if and only if G is a path of length one.
Theorem 3.6. Let G be a simple connected graph, then

In the above inequality equality holds if and only if all the vertices of G are of same eccentricity.
Proof Since,

for , we have
, we have

from where we get the desired result. Obviously in the above inequality equality holds if and only if all the vertices of G are of same eccentricity.
Corollary 3.2. Let G be a simple connected graph with n vertices and m edges, then

with equality if and only if  or G is obtained from Kn by removing a perfect matching.
or G is obtained from Kn by removing a perfect matching.
Proof Since we have [8],  , with equality if and only if
, with equality if and only if  for
for  or
or , from the above theorem the desired result follows.
, from the above theorem the desired result follows.
4. Conclusion
In this paper we have established some sharp upper and lower bounds of the Zagreb eccentricity indices in terms of some graph parameters such as order, size, radius, diameter, eccentric connectivity index, total eccentricity, first and second Zagreb indices. It may be useful to give the bounds for E1(G) and E2(G) indices in terms of other graph invariants.