1. Introduction
A knight’s tour on a chessboard is a path, consisting of at least two moves, in which the knight chess piece visits each square on the chessboard exactly once. In a closed knight’s tour, the knight returns to the square on which it started. In an open knight’s tour, the knight does not return to its starting square. For the purpose of this paper, any mention of knight’s tours will refer to closed knight’s tours, unless specified otherwise. In terms of graph theory, finding a knight’s tour on an  chess-board is equivalent to finding a Hamiltonian cycle made up of knight’s moves on an
chess-board is equivalent to finding a Hamiltonian cycle made up of knight’s moves on an  graph, where the squares are the nodes and the moves are the edges.
graph, where the squares are the nodes and the moves are the edges.
Euler worked on knight’s tours. He constructed an 8 × 8 closed tour by joining open tours on two 4 × 8 boards [1, pp. 6-7]. The technique of combining two tours to create another tour is commonly used today for constructing knight’s tours. In 1991, Allen Schwenk settled the question of which  chessboards contain knight’s tours and which do not [2].
chessboards contain knight’s tours and which do not [2].
Subsequently, interest shifted to the existence of knight’s tours on chess-boards with squares removed. DeMaio and Hippchen [3] presented a function whose value on any rectangular board is the number of squares that must be removed so that the board will have a closed knight’s tour. They determined that the removal of one square permits a knight’s tour on all  boards with n odd, except for n = 5. The particular location of the removed square or squares is unimportant for their results, but it cannot be an arbitrary square. They give some speci? C examples such as closed knight’s tours on a 3 × 7 board with square (2, 2) removed and on a 3 × 9 board with square (3, 5) removed.
boards with n odd, except for n = 5. The particular location of the removed square or squares is unimportant for their results, but it cannot be an arbitrary square. They give some speci? C examples such as closed knight’s tours on a 3 × 7 board with square (2, 2) removed and on a 3 × 9 board with square (3, 5) removed.
We determine which  chessboards have a closed knight’s tour, when each square is removed in turn.
chessboards have a closed knight’s tour, when each square is removed in turn.
We color chessboards with alternating black and white squares and the upper-left corner square black, so that where matrix notation is used squares (i, j) with i + j odd are white.
2. Knight’s Tours on 3 × n Boards with a Single Square Removed
In this section, we show that all 3 × n boards with one square removed contain a knight’s tour, except for those listed in Lemma 1.
Lemma 1. A knight’s tour does not exist on a 3 × n chessboard with one square removed if:
n is eventhe removed square is (i, j) with i + j oddn = 1n = 3 when any square other than the center square is removedn = 5n = 7 when any square other than square (2, 2) or (2, 6) is removedn = 9 when square (1, 3), (3, 3), (1, 7), (3, 7), (2, 4), (2, 6), (2, 2), or (2, 8) is removed, or
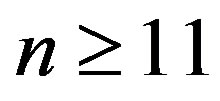 when square (1, 3), (2, 4), (3, 3), (1, n – 2), (2, n – 3), or (3, n – 2) is removed.
when square (1, 3), (2, 4), (3, 3), (1, n – 2), (2, n – 3), or (3, n – 2) is removed.
Proof. Because each knight’s move alternates colors, for a tour to exist, there must be an equal number of black and white squares and an even number of total squares. This implies that for a knight’s tour to exist on an m × n chessboard with one square removed, both m and n must be odd and the removed square must be black. So, on a 3 × n board with one square removed, a tour cannot exist if n is even or the removed square is (i, j) with i + j odd. The 3 × 1 board does not contain a knight’s tour because the knight is unable to move in the horizontal direction.
Knight’s moves are often forced on 3 × n boards. Figure 1 shows the cycle that is forced on the 3 × 3 board. Square (1, 1) is forced to connect to squares (3, 2) and (2, 3), square (2, 1) is forced to connect to squares (1,3) and (3, 3), and so forth. Eventually, a cycle is created that goes through all squares except for the center square. If any square other than the center square is removed, the knight ends up stuck and unable to move. This proves that a knight’s tour cannot exist on the 3 × 3 board if any square other than the center square is removed.
Figure 2 shows that each corner square on the 3 × 5 board is forced to connect to the center square. For a knight’s tour to exist, each square must have exactly two connecting edges. Even if one corner square is removed from the 3 × 5 board, the center square still has 3 connecting edges, preventing the existence of a knight’s tour.
A knight’s tour cannot exist if a non-Hamiltonian cycle is forced on a chessboard because a non-Hamiltonian cycle prevents the knight from visiting each square. Figure 3 shows the cycle that is forced on the 3 × 7 board. Squares (2, 2) and (2, 6) are each forced to connect to squares (1, 4) and (3, 4). The forced cycle can be broken if either of these four squares is removed. However, the removal of square (1, 4) or (3, 4) leaves the knight on square (2, 2) and (2, 6) unable to move. Therefore, if any square other than square (2, 2) or (2, 6)

Figure 1. Forced cycle on the 3 × 3 board.

Figure 2. Forced edges on the 3 × 5 board.

Figure 3. Forced cycle on the 3 × 7 board.
is removed, no tour can exist on the 3 × 7 board.
Figure 4 shows edges that are forced on the 3 × 9 board. Square (2, 1) is forced to connect to squares (1, 3) and (3, 3) and square (2, 9) is forced to connect to squares (1, 7) and (3, 7). This shows that squares (1, 3), (3, 3), (1, 7), and (3, 7) cannot be removed from the 3 × 9 board. If they are removed, the knight on square (2, 1) or (2, 9) becomes unable to move.
Figure 4 also shows that, unless a corner square is removed, square (2, 3) is forced to connect to squares (1, 1) and (3, 1) and square (2, 7) is forced to connect to squares (1, 9) and (3, 9). This makes squares (2, 3) and (2, 7) unattainable to the knight on any other square.
Figure 5 shows the cycle that is forced on the 3 × 9 board if square (2, 4) is removed. Square (2, 2) is forced to connect to squares (1, 4) and (3, 4) and square (2, 8) is forced to connect to squares (1, 6) and (3, 6). Because squares (2, 3) and (2, 7) are unattainable, square (1, 5) is forced to connect to squares (3, 4) and (3, 6), and square (3, 5) is forced to connect to squares (1, 4) and (1, 6), thus producing a cycle. This proves that square (2, 4) cannot be removed from the 3 × 9 board. Due to the symmetry of the 3 × 9 board, showing that square (2, 4) cannot be removed also shows that square (2, 6) cannot be removed.
Figure 6 shows the cycle that is forced on the 3 × 9 board if square (2, 2) is removed. Square (2, 8) is forced to connect to squares (1, 6) and (3, 6). Because squares (2, 3) and (2, 7) are unattainable, square (1, 5) is forced to connect to squares (3, 4) and (3, 6), and square (3, 5) is forced to connect to squares (1, 4) and (1, 6). Since squares (1, 6) and (3, 6) have two connecting edges,

Figure 4. Forced edges on the 3 × 9 board.

Figure 5. Forced cycle on the 3 × 9 board when square (2, 4) is removed.

Figure 6. Forced cycle on the 3 × 9 board when square (2, 2) is removed.
square (2, 4) must connect to squares (1, 2) and (3, 2), thus producing a cycle. Figure 6 shows that squares (2, 2) and (2, 8) cannot be removed from the 3 × 9 board.
Figures 7 and 8 show the six squares that can never be removed from 3 × n boards, when n is odd and greater than or equal to 11. As seen in Figure 7, removing square (1, 3), (3, 3), (1, n – 2) or (3, n – 2) leaves the knight on square (2, 1) or (2, n) unable to move. Figure 8 shows the cycles that are forced if square (2, 4) or (2, n – 3) is removed.
Lemma 2. A knight’s tour exists on a 3 × n chessboard with one square removed if:
n = 3 when the center square is removedn = 7 when square (2, 2) or (2, 6) is removedn = 9 when square (1, 1), (1, 5), (3, 1), (3, 5), (1, 9), or (3, 9) is removed, or
 and odd when any square (i, j) with i + j even other than (1, 3), (2, 4) (3, 3), (1, n – 2), (2, n – 3), or (3, n – 2) is removed.
and odd when any square (i, j) with i + j even other than (1, 3), (2, 4) (3, 3), (1, n – 2), (2, n – 3), or (3, n – 2) is removed.
Proof. The forced cycle on the 3 × 3 board, shown in Figure 1, is a knight’s tour when the center square is removed. Table 1 shows a knight’s tour on the 3 × 7 board when square (2, 2) is removed. In this figure, the numbers on the squares represent the order in which the knight visits each square. For example, the knight starts on square 1, then moves to square 2, then to square 3,

Figure 7. Forced edges on 3 × n boards, n odd and greater than or equal to 11, that prevent the removal of squares (1, 3), (3, 3), (1, n – 2), and (3, n – 2).

Figure 8. Forced cycles on 3 × n boards, n odd and greater than or equal to 11, when square (2, 4) or (2, n – 3) is removed.
Table 1. 3 × 7 tour with square (2, 2) removed.

and so forth. “Hole” indicates the removed square. Due to the symmetry of the 3 × 7 board, showing that the removal of square (2, 2) permits a tour also shows that the removal of square (2, 6) permits a tour. In the same way, Tables 2 and 3 show that the removal of the corner squares and squares (1, 5) and (3, 5) permit a knight’s tour on the 3 × 9 board.
Tables 4-7 show that all black squares can be removed from the 3 × 11 board, except for squares (1, 3), (2, 4), (3, 3), (1, 9), (2, 8), and (3, 9). These 3 × 11 tours can be extended into 3 × (11 + 4) tours using the 3 × 4 extender board shown in Table 8. The regular 3 × 11 knight’s tour is followed from square (1, 1) through square (3, 11) on the 3 × 11 board. The 3 × 11 tour is then broken as the knight jumps from square (3, 11) on the 3 × 11 board to square (1, 1) on the extender board. The tour continues throughout the extender board until it reaches square (2, 1). The tour continues back into the 3 × 11 board as the knight jumps from square (2, 1) on the extender board to square (1, 10) on the 3 × 11 board and continues the rest of the 3 × 11 tour. The extender board was used in a similar way in [1, p. 46], [2, p. 329], and [3, p. 221].
Two 3 × 4 extender boards can be combined to make a 3 × 8 extender board. Therefore, any 3 × 11 tour can be extended into a 3 × (11 + 4 k) tour, k = 1, 2, 3,···. This proves that all black squares can be removed from 3 × n boards, n ≥ 11, n ≡ 3 mod 4, n odd, except for the six squares that were specified in Lemma 1.
Table 2. 3 × 9 tour with square (3, 1) removed.

Table 3. 3 × 9 tour with square (1, 5) removed.

Table 4. 3 × 11 tour with square (2, 2) removed.

Table 5. 3 × 11 tour with square (2, 6) removed.

Table 6. 3 × 11 tour with square (1, 11) removed.

Table 7. 3 × 11 tour with square (1, 5) removed.

Table 8. 3 × 4 extender board.

Specifically, all black squares can be removed from 3 × n boards, n ≥ 13, n ≡ 1 mod 4, n odd, except for the six squares that were specified in Lemma 1. Tables 9-13 show with examples that all black squares can be removed from a 3 × 13 board, except for squares (1, 3), (2, 4), (3, 3), (1, 11), (2, 10), and (3, 11). The 3 × 4
Table 9. 3 × 13 tour with square (3, 1) removed.

Table 10. 3 × 13 tour with square (2, 2) removed.

Table 11. 3 × 13 tour with square (1, 5) removed.

Table 12. 3 × 13 tour with square (2, 6) removed.

Table 13. 3 × 13 tour with square (1, 7) removed.

extender board can also expand these 3 × 13 tours into 3 × (13 + 4 k) tours, k = 1, 2, 3,··· .
Combining Lemmas 1 and 2 gives Theorem 1.
Theorem 1. A knight’s tour exists on all 3 × n chessboards with one square removed except for the boards listed in Lemma 1.