 ,
,  ,
,
subject to the right focal type two-point boundary conditions
 ,
, 
 ,
, .
.
We establish a criterion for the existence of at least one positive solution by utilizing Krasnosel’skii fixed point theorem. And then, we establish the existence of at least three positive solutions by utilizing Leggett-Williams fixed point theorem.
1. Introduction
The study of the existence of positive solutions of boundary value problems (BVPs) for higher order differential equations on time scales has gained prominence and it is a rapidly growing field, since it arises, especially for higher order differential equations on time scales arise naturally in technical applications. Meyer [1], strictly speaking, boundary value problems for higher order differential equation on time scales are a particular class of interface problems. One example in which this is exhibited is given by Keener [2] in determining the speed of a flagellate protozoan in a viscous fluid. Another particular case of a boundary value problem for a higher order differential equation on time scales arising as an interface problem is given by Wayner, et al. [3] in dealing with a study of perfectly wetting liquids. In these applied settings, only positive solutions are meaningful. By a time scale we mean a nonempty closed subset of . For the time scale calculus and notation for delta differentiation, integration, as well as concepts for dynamic equation on time scales we refer to the introductory book on time scales by Bohner and Peterson [4], and denote the time scales by the symbol
. For the time scale calculus and notation for delta differentiation, integration, as well as concepts for dynamic equation on time scales we refer to the introductory book on time scales by Bohner and Peterson [4], and denote the time scales by the symbol .
.
By an interval we mean the intersection of the real interval with a given time scale. The existence of positive solutions for BVPs has been studied by many authors, first for differential equations, then finite difference equations, and recently, unifying results for dynamic equations. We list some papers, Erbe and Wang [5], and Eloe and Henderson [6,7], Atici and Guseinor [8], and Anderson and Avery [9], and Avery and Peterson [10], Agarwal, Regan and Wang [11], Deimling [12], Gregus [13] Guo and Lakshmikantham [14], Henderson and Ntouyas [15], Hopkins [16] and Li [17]. Recently, in 2008, Moustafa Shehed [18] obtained at least one positive solution to the boundary value problem

This paper considers the existence of positive solutions to  order nonlinear differential equation on time scales
order nonlinear differential equation on time scales
 (1)
(1)
subject to the right focal type boundary conditions
 (2)
(2)
 (3)
(3)
These boundary conditions include different types of right focal boundary conditions.
We make the following assumptions throughout:
(A1)  is continuous with respect to
is continuous with respect to  where
where  is nonnegative real numbers(A2) The point t in
is nonnegative real numbers(A2) The point t in  is not left dense and right scattered at the same time.
is not left dense and right scattered at the same time.
Define the nonnegative extended real numbers ,
,  ,
,  and
and  by
by



and

This paper is organized as follows; In Section 2, we estimate the bounds for the Greens function which are needed for later discussions. In Section 3, we establish a criteria for the existence of at least one positive solution for the BVP by using Krasnosel’skii fixed point theorem. In Section 4, we establish the existence of at least three positive solutions for the BVP by using Leggett-Williams fixed point theorem. Finally, as an application, we give some examples to demonstrate our result.
2. Green’s Function and Bounds
In this section, first we state a Lemma to compute delta derivatives for , next, construct a Green’s function for homogeneous two point BVP
, next, construct a Green’s function for homogeneous two point BVP  with (2), (3) and estimate the bounds to the Green’s function.
with (2), (3) and estimate the bounds to the Green’s function.
Lemma 2.1. Let , define a function
, define a function  by
by , if we assume that the conditions (A2) and (A3) are satisfied, then
, if we assume that the conditions (A2) and (A3) are satisfied, then
 (4)
(4)

holds for all  where
where  is the set of all distinct combinations of
is the set of all distinct combinations of  such that the sum is equal to given
such that the sum is equal to given .
.
Proof see [19].
We denote


Theorem 2.2. Green’s function for the homogeneous BVP

with the boundary conditions (2), (3) is given by

where

for all 
Proof: It is easy to check that the BVP  with the boundary conditions (2) and (3) has only trivial solution. Let
with the boundary conditions (2) and (3) has only trivial solution. Let  be the Cauchy function for
be the Cauchy function for , and is given by
, and is given by

For each fixed  let
let  be the unique solution of the BVP
be the unique solution of the BVP

and


Since

are the solutions of 

By using boundary conditions,  ,
,  , we have
, we have . Therefore
. Therefore

Since,

It follows that

Hence  has the form for
has the form for 

And for ,
, . It follows that
. It follows that

where


Lemma 2.3. For , we have
, we have
 (5)
(5)
Proof: For , we have
, we have

Similarly, for  we have
we have  Thus, we have
Thus, we have

for all 

Lemma 2.4. Let . For
. For , we have
, we have
 (6)
(6)
Proof: The Green’s function  for the homogeneous BVP corresponding to (1)-(3) is positive on
for the homogeneous BVP corresponding to (1)-(3) is positive on 
For  and
and , we have
, we have

Similarly, for  and
and  we have
we have


3. Existence of at Least One Positive Solution
In this section, we establish a criteria for the existence of at least one positive solution of the BVP (1)-(3). Let  be the solution of the BVP (1)-(3), and is given by
be the solution of the BVP (1)-(3), and is given by
 (7)
(7)
for all 
Define  with the norm
with the norm

Then  is a Banach space. Define a set
is a Banach space. Define a set  by
by
 (8)
(8)
We define the operator  by
by
 (9)
(9)
for all 
Theorem 3.1. (Krasnosel’skii) Let  be a Banach space,
be a Banach space,  be a cone, and suppose that
be a cone, and suppose that ,
,  are open subsets of
are open subsets of  with
with 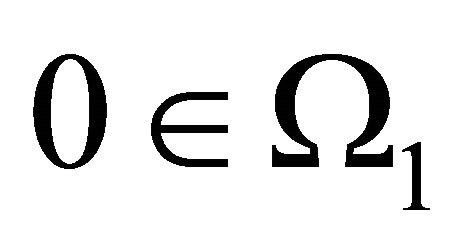 and
and . Suppose further that
. Suppose further that  is completely continuous operator such that either 1)
is completely continuous operator such that either 1) ,
,  and
and ,
,  , or 2)
, or 2) ,
,  and
and ,
,  holds. Then T has a fixed point in
holds. Then T has a fixed point in 
Theorem 3.2. If  and
and , then the BVP (1)-(3) has at least one positive solution that lies in
, then the BVP (1)-(3) has at least one positive solution that lies in .
.
Proof: We seek a fixed point of T in . We prove this by showing the conditions in Theorem 3.1 hold.
. We prove this by showing the conditions in Theorem 3.1 hold.
First, if , then
, then

so that

Next, if , then
, then

Hence, . Standard argument involving the Arzela-Ascoli theorem shows that T is completely continuous operator. Since
. Standard argument involving the Arzela-Ascoli theorem shows that T is completely continuous operator. Since , there exist
, there exist  and
and
 such that
such that  for
for
 , and
, and  Let us choose
Let us choose
 with
with . Then, we have from Lemma 2.3,
. Then, we have from Lemma 2.3,

Therefore,  Hence, if we set
Hence, if we set

Then
 (10)
(10)
Since , there exist
, there exist  and
and  such that
such that , for
, for  and
and  If we set
If we set

and define

If , so that
, so that , then
, then

And we have

Thus,  , and so
, and so
 (11)
(11)
An application of Theorem 3.1 to (10) and (11) yields a fixed point of  that lies in
that lies in . This fixed point is a solution of the BVP (1)-(3).
. This fixed point is a solution of the BVP (1)-(3). 
Theorem 3.3. If  and
and , then the BVP (1)-(3) has at least one positive solution that lies in
, then the BVP (1)-(3) has at least one positive solution that lies in .
.
Proof: Let T be the cone preserving, completely continuous operator defined as in (9). Since , there exist
, there exist  and
and  such that
such that
 for
for , and
, and
 In this case, define
In this case, define
 Then, for
Then, for  we have
we have 
 and moreover,
and moreover,
 ,
, . Thus
. Thus

From which we have
 (12)
(12)
It remains for us to consider , in this case, there exist
, in this case, there exist  and
and  such that
such that
 , for
, for , and
, and
 There are two subcases.
There are two subcases.
Case (i)  is bounded. Suppose
is bounded. Suppose  is such that
is such that , for all
, for all .
.
Let  and let
and let

Then, for , we have
, we have

and so
 (13)
(13)
Case (ii) f is unbounded. Let  be such that
be such that  for
for . Let
. Let

Choosing ,
,

And so
 (14)
(14)
An application of Theorem 3.1, to (12), (13) and (14) yields a fixed point of  that lies in
that lies in . This fixed point is a solution of the BVP (1)-(3).
. This fixed point is a solution of the BVP (1)-(3). 
4. Existence of Multiple Positive Solutions
In this section, we establish the existence of at least three positive solutions to the BVP (1)-(3).
Let  be a real Banach space with cone
be a real Banach space with cone . A map
. A map  is said to be a nonnegative continuous concave functional on
is said to be a nonnegative continuous concave functional on , if
, if  is continuous and
is continuous and

for all  and
and  Let
Let  and
and  be two real numbers such that
be two real numbers such that  and
and  be a nonnegative continuous concave functional on
be a nonnegative continuous concave functional on . We define the following convex sets
. We define the following convex sets


We now state the famous Leggett-Williams fixed point theorem.
Theorem 4.1. See ref. [20] Let  be completely continuous and S be a nonnegative continuous concave functional on P such that
be completely continuous and S be a nonnegative continuous concave functional on P such that  for all
for all . Suppose that there exist
. Suppose that there exist ,
,  ,
,  , and
, and  with
with  such that 1)
such that 1)  and
and  for
for 
2)  for
for 
3)  for
for  with
with 
Then  has at least three fixed points
has at least three fixed points ,
,  ,
,  in
in  satisfying
satisfying

For convenience, we let


Theorem 4.2. Assume that there exist real numbers ,
,  , and c with
, and c with  such that
such that
 (15)
(15)
 (16)
(16)
 (17)
(17)
Then the BVP (1)-(3) has at least three positive solutions.
Proof: Let the Banach space  be equipped with the norm
be equipped with the norm

We denote

Then, it is obvious that P is a cone in E. For , we define
, we define

It is easy to check that  is a nonnegative continuous concave functional on
is a nonnegative continuous concave functional on  with
with  for
for  and that
and that  is completely continuous and fixed points of
is completely continuous and fixed points of  are solutions of the BVP (1)-(3). First, we prove that if there exists a positive number
are solutions of the BVP (1)-(3). First, we prove that if there exists a positive number  such that
such that
 for
for , then
, then . Indeed, if
. Indeed, if , then for
, then for .
.

Thus,  , that is,
, that is,  Hence, we have shown that if (15) and (17) hold, then
Hence, we have shown that if (15) and (17) hold, then  maps
maps  into
into  and
and  into
into . Next, we show that
. Next, we show that
 and
and  for all
for all . In fact, the constant function
. In fact, the constant function

Moreover, for , we have
, we have

for all . Thus, in view of (16) we see that
. Thus, in view of (16) we see that

as required. Finally, we show that if  and
and , then
, then . To see this, we suppose that
. To see this, we suppose that  and
and , then, by Lemma 2.4, we have
, then, by Lemma 2.4, we have

for all . Thus
. Thus

To sum up the above, all the hypotheses of Theorem 4.1 are satisfied. Hence  has at least three fixed points, that is, the BVP (1)-(3) has at least three positive solutions
has at least three fixed points, that is, the BVP (1)-(3) has at least three positive solutions ,
,  and
and  such that
such that


5. Examples
Now, we give some examples to illustrate the main result.
Example 1
Consider the following boundary value problem
 (18)
(18)
The Green’s function for the homogeneous boundary value problem is given by

It is easy to see that all the conditions of Theorem 3.2 hold. It follows from Theorem 3.2, the BVP (18) has at least one positive solution.
Example 2
Consider the following boundary value problem
 (19)
(19)
The Green’s function for the homogeneous boundary value problem is given by

It is easy to see that all the conditions of Theorem 3.3 hold. It follows from Theorem 3.3, the BVP (19) has at least one positive solution.
Example 3
Consider the following boundary value problem on time scale
 (20)
(20)
where

The Green’s function for the homogeneous boundary value problem is given by

A simple calculation shows that ,
,
 and
and . If we choose
. If we choose ,
, 
and  then, we see that all the conditions of Theorem 4.2 hold. It follows from Theorem 4.2, the BVP (20) has at least three positive solutions.
then, we see that all the conditions of Theorem 4.2 hold. It follows from Theorem 4.2, the BVP (20) has at least three positive solutions.
6. Conclusion
In this paper, we have established the existence of positive solutions for higher order boundary value problems on time scales which unifies the results on continuous intervals and discrete intervals, by using Leggett-Williams fixed point theorem. These results are rapidly arising in the field of modelling and determination of flagellate protozoan in a viscous fluid in further research.