Neutrino Oscillations and Superluminal Propagation, in OPERA or Otherwise ()
1. Introduction
No particle can claim to have caused as much havoc in modern physics as the neutrino. Ever since its proposal by Pauli in 1930, the neutrino has been the source of relentless mischief, with its parity violating properties supplying the prime example. The propensity of neutrino flavors to oscillate comes a close second. Neutrino oscillations have now evolved from the wild idea first suggested by Pontecorvo [1-3] into a respectable fact. Against this historical background one should perhaps not be overly surprised by recent claims that superluminal speeds have been achieved by neutrinos [4]. As with any experimental result, these claims should be taken with a macroscopic grain of salt. The potential for uncharted systematic errors can never be overemphasized [5,6]. Nonetheless, theorists are easily excitable creatures who don’t require much prompting before going down the “what if” alley [7,8]. The purpose of this paper is to follow this time honored tradition, exploring the implications of the possible superluminal nature of the neutrino for the general theory of oscillations, and also for theories proposing faster than light propagation in cosmology [9-11].
It is undeniable that the alleged neutrino superluminal behaviour sits uncomfortably in our theoretical constructions, even those tailored to accommodate the strangest behaviour. Faster than light propagation has been envisaged in the context of varying speed of light theories, in particular those where the speed of light is energy dependent [12-15]. The latter may be realized in a variety of ways, for example via a deformation of the usual dispersion relations, then made invariant by adopting a nonlinear representation of the Lorentz group [16]. This approach was actually applied to neutrinos a few years back [17,18], where it was shown that with minimal assumptions, and without assuming tachyonic behaviour for the mass states, it is possible for the flavor states to display features peculiar to tachyons, e.g. regarding the end point of beta decay (see, e.g. [19]). However, it was stressed that in such theories the neutrino would always remain slower than light. In this paper we identify the assumptions that must be broken for superluminal behaviour to be unleashed. We start with the construction of [17,18], but then consider more general theories as well. A measure of contrived success is achieved.
The quantum field theory of neutrinos has been the subject of some debate. We do not want to wed our considerations to this debate, but since one of our models results from this discussion we briefly review the issues at stake. It was shown in [20] that it is possible to define a Hilbert space of flavor states, with a well defined vacuum state and creation and annihilation operators. Comparison with the usual treatment shows that this approach amounts to a different choice of vacuum. The matter is far from pedantic and corrections to the usual formula for neutrino oscillations arise [21]. Flavor states constructed in this way are eigenstates of the flavor charge and the momentum operators but are not eigenstates of the Hamiltonian [21-26]. Nonetheless one can compute the expectation value of the Hamiltonian  on the flavor states and define from it dispersion relations. These dispersion relations are not the usual hyperbolic ones and fall within the remit of deformed special relativity, as explained in [17]. One may then wonder under what circumstances these theories could accommodate superluminal neutrino speeds, in line with the theories considered in [12-16].
on the flavor states and define from it dispersion relations. These dispersion relations are not the usual hyperbolic ones and fall within the remit of deformed special relativity, as explained in [17]. One may then wonder under what circumstances these theories could accommodate superluminal neutrino speeds, in line with the theories considered in [12-16].
To illustrate our point we shall consider the simplifying case of two flavors, and examine Pontecorvo states (thereby neglecting a number of subtleties with the set up of the flavor Hilbert space; see [18]). We then have the generic mixing relations for flavors  and
and 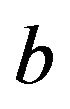 (which could be the muon and the tauon or the electron and the muon):
(which could be the muon and the tauon or the electron and the muon):
 (1)
(1)
Without loss of generality we take  and
and
 . Computing the expectation value of the Hamiltonian on the flavor states (1) we find:
. Computing the expectation value of the Hamiltonian on the flavor states (1) we find:
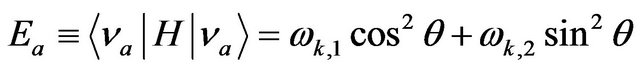 (2)
(2)
 (3)
(3)
where 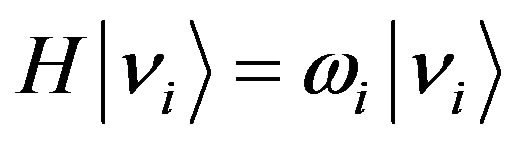
 and
and
 (4)
(4)
Since the sum of two square roots is generally not a square root, except for trivial cases, flavor states do not satisfy hyperbolic dispersion relations. If we take seriously the flavor states thus constructed, and if we wish to avoid a conflict with the principle of relativity, we should therefore postulate that flavor states transform according to a non-linear representation of the Lorentz group [15, 16]. Following the derivation in [17], the dispersion relations (2) may be cast in the form:
 (5)
(5)
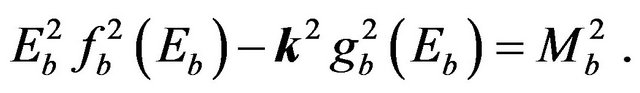 (6)
(6)
from which the recipes given in [16] for the construction of the non-linear representation are straightforward to apply. Specifically, Equation (2) leads to
 (7)
(7)
 (8)
(8)
from which one finds
 (9)
(9)
 (10)
(10)
 (11)
(11)
The above assumes . For maximal mixing,
. For maximal mixing,  , we have instead:
, we have instead:
 (12)
(12)
 (13)
(13)
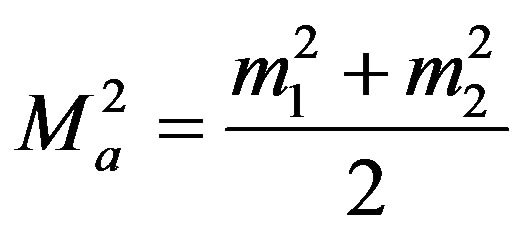 (14)
(14)
Similar expressions, but with , apply to flavor
, apply to flavor . A number of corrections arise from a more careful treatment [18], but they do not qualitatively change the rest of our discussion.
. A number of corrections arise from a more careful treatment [18], but they do not qualitatively change the rest of our discussion.
It was noted in [17] that even with non-tachyonic mass states 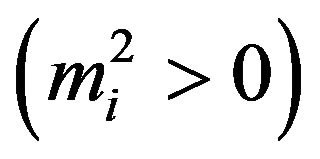 it is possible to obtain
it is possible to obtain  for
for
 (15)
(15)
This has a number of interesting implications concerning the end point of beta decay, which can indeed be as one would expect from a tachyonic neutrino. But the interesting point made in [17] is that this can be accomplished without the usual pathologies of tachyons. Unlike tachyons, there is not a minimal non-vanishing momentum, for which the energy is zero, connecting the positive and negative branch of the dispersion relations thereby leading to a runaway instability. On the contrary it is easy to check that the flavor states can have , at which point they reach their minimal non-zero energy:
, at which point they reach their minimal non-zero energy:
 (16)
(16)
 (17)
(17)
In addition these dispersion relations do not entail superluminal propagation. They imply a propagation velocity (assuming the concept applies to flavor states), which is a monotonically growing function of the momentum which always satisfies . This is true for both phase speed
. This is true for both phase speed  or group speed
or group speed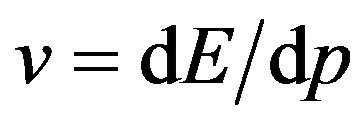 , and is hardly news. Starting from (2) and (3) we may rewrite the dispersion relations in the ultra-relativistic regime as:
, and is hardly news. Starting from (2) and (3) we may rewrite the dispersion relations in the ultra-relativistic regime as:
 (18)
(18)
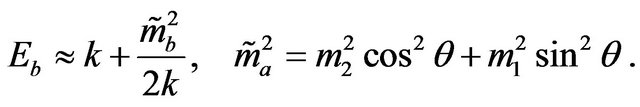 (19)
(19)
Non-tachyonic mass states therefore ensure nontachyonic behavior for the flavor states in the relativistic regime. Regrettably (or perhaps not) the tachyons found in [17] only behave like tachyons at low energies, and even then within a limited scope. The implication is that some assumption in this very minimal model must be dropped if we want to accommodate superluminal speeds. This result is not very surprising. With the very conventional assumptions we have made one may take the view that the only states with a well defined (phase or group) speed are the mass eigenstates. If none of these are tachyonic then no superluminal behavior can be expected.
A possible new ingredient is to postulate that one of the mass eigenstates is tachyonic. Then superluminal behavior can be expected, even if no other assumptions are changed. The formalism we have presented, however, introduces an interesting novelty. We find that neutrino oscillations cure a fundamental tachyonic pathology. Continuing to illustrate our point with the simplified model presented above, let us assume that the first mass state is tachyonic, i.e. . Neutrino mixing superposes particles with the same momentum, so we are forced to conclude that both flavor states,
. Neutrino mixing superposes particles with the same momentum, so we are forced to conclude that both flavor states,  and
and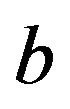 , have a non-vanishing minimum momentum,
, have a non-vanishing minimum momentum,  , just like any tachyon. However, unlike standard tachyons, the energy at this point is not zero, but the minimal energy:
, just like any tachyon. However, unlike standard tachyons, the energy at this point is not zero, but the minimal energy:
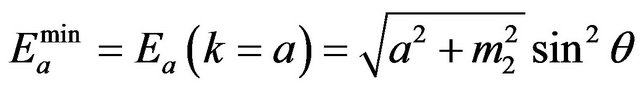 (20)
(20)
 (21)
(21)
As with standard particles, or “bradyons”, there is of course a negative energy branch, but there is a gap between the two preventing runaway instabilities. Given that interactions are mediated via flavor states, we can argue that it is their dispersion relations, and not those of the mass eigenstates, which are relevant for stability discussions. Therefore an unsavory property of tachyons seems to have been removed from the problem. This is an interesting twist on the tachyonic neutrinos of [27,28].
In spite of this novelty, the flavor states are not regular bradyons. As one can read off from (18), if:
 (22)
(22)
the flavor  has tachyonic properties at high energies, unlike the case discussed in [17]. Assuming the tachyonic behaviour seen by [4] is due to a mass eigenstate we should have
has tachyonic properties at high energies, unlike the case discussed in [17]. Assuming the tachyonic behaviour seen by [4] is due to a mass eigenstate we should have  which is uncomfortably high. With a flavor state taking the blame the condition would become more flexible:
which is uncomfortably high. With a flavor state taking the blame the condition would become more flexible:
 (23)
(23)
Choosing a single tachyonic mass state, may lead to other problems, such as a detrimental effect on the coherence length of the neutrino (but note that oscillation formulas have to be rederived in this case). However, the argument above can be repeated if more than one mass eigenstate is tachyonic. In the two flavor example we have chosen, if  and
and , with
, with , then the minimal momentum is
, then the minimal momentum is , for which the energies are
, for which the energies are
 (24)
(24)
 (25)
(25)
and the argument still carries through.
Is there any way of achieving the same effect with non-tachyonic mass states within the usual theory of oscillations? We were unable to find one, but what we have said so far suggests obvious modifications to the theory, capable of accomplishing the task. Suppose that at some energy  the flavor states become eingenstates of the Hamilton endowed with the dispersion relations (5) and (6). Suppose further that at this scale
the flavor states become eingenstates of the Hamilton endowed with the dispersion relations (5) and (6). Suppose further that at this scale  goes to 1 faster than
goes to 1 faster than , say by replacing
, say by replacing
 (26)
(26)
Then, at low energies everything we have said still stands, but at high energies we fail to witness the transition from mass  (assuming condition (15)) to mass
(assuming condition (15)) to mass . Quite the opposite: the mass remains
. Quite the opposite: the mass remains  at high energies. Therefore, as in [17], the minimal energy of flavor
at high energies. Therefore, as in [17], the minimal energy of flavor  is
is  given by (16), and is achieved with
given by (16), and is achieved with . But then we must cross-over from the bradyonic to the tachyonic quadrant. As the energy increases, the neutrino goes from
. But then we must cross-over from the bradyonic to the tachyonic quadrant. As the energy increases, the neutrino goes from  to break the speed of light barrier at
to break the speed of light barrier at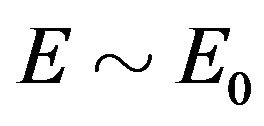 , reaching a maximal speed before slowing down to
, reaching a maximal speed before slowing down to  from above, as the energy goes to infinity. As in the cases discussed above, no instabilities are present, but obviously superluminal behavior is obtained. Once we have accepted this sort of dispersion relation we could postulate something similar for the mass eigenstates and keep the standard theory of oscillations. Note that with the assumption that the flavor states diagonalize the eigenstates at high energies
from above, as the energy goes to infinity. As in the cases discussed above, no instabilities are present, but obviously superluminal behavior is obtained. Once we have accepted this sort of dispersion relation we could postulate something similar for the mass eigenstates and keep the standard theory of oscillations. Note that with the assumption that the flavor states diagonalize the eigenstates at high energies  we would predict no oscillations.
we would predict no oscillations.
Once we go beyond conventional theory, why not tie in these results with other non-conventional theories. However, as was pointed out in [7], appealing to Planck scale effects known to raise the speed of light does not blend nicely with the observations of [4]. Suppose, as an example, that we take
 (27)
(27)
for the base dispersion relations, applicable to all particles, and so presumably also to the neutrino mass eigenstates. This theory has  as the maximal momentum and displays a varying speed of light [16]. This propagates into the speed for a neutrino mass state
as the maximal momentum and displays a varying speed of light [16]. This propagates into the speed for a neutrino mass state  as:
as:
 (28)
(28)
For a standard neutrino scenario the last term is negligible  and so, looking at the first term, we’d need the Planck mass to be of order
and so, looking at the first term, we’d need the Planck mass to be of order  (rather than the conventional
(rather than the conventional ) to explain the observations. Even then we’d need to explain why the effect hadn’t been observed in other particles, well explored in this energy range. The neutrino would have to be unique in its probe of this dispersion relation.
) to explain the observations. Even then we’d need to explain why the effect hadn’t been observed in other particles, well explored in this energy range. The neutrino would have to be unique in its probe of this dispersion relation.
While we agree with [7] in this respect1, we note that once we accept that the neutrino would have to have unique dispersion relations, not shared by other particles, the situation improves. Indeed then it would be possible to explain the magnitude of the observed effect without making the Planck scale unduly small. This could be done with a sort of “seesaw mechanism”. As an illustrative example, suppose that neutrino mass states feel dispersion relations of the type:
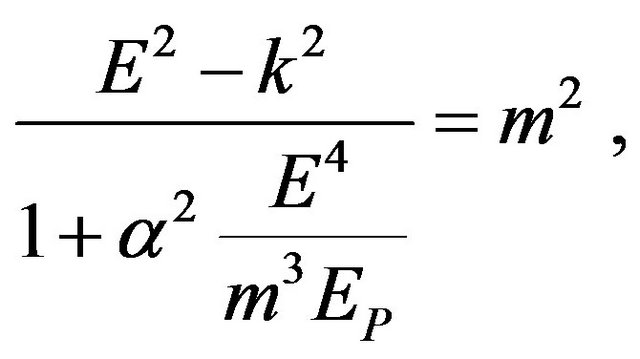 (29)
(29)
where  is a dimensionless parameter. Since the dispersion relation is specific to neutrinos we shouldn’t be alarmed to see
is a dimensionless parameter. Since the dispersion relation is specific to neutrinos we shouldn’t be alarmed to see  appear in the deformation, as well as
appear in the deformation, as well as . Then superluminal effects would kick in for
. Then superluminal effects would kick in for . Moreover, we could accommodate the results in 4] with
. Moreover, we could accommodate the results in 4] with 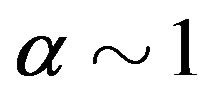 (i.e. no fine tuning), since the neutrino speed would satisfy:
(i.e. no fine tuning), since the neutrino speed would satisfy:
 (30)
(30)
Again the first term is negligible in the context of [4] while the second explains the observation. The crucial aspect in this argument is that the energy in the neutrino beam  misses the geometrical average of the neutrino mass scale (say
misses the geometrical average of the neutrino mass scale (say ) and the standard Planck scale
) and the standard Planck scale  by a factor of order
by a factor of order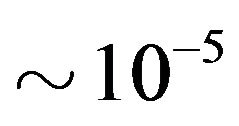 : precisely the observed fractional superluminal propagation speed. We may not want to indulge in numerology, but we can make use of it.
: precisely the observed fractional superluminal propagation speed. We may not want to indulge in numerology, but we can make use of it.
In summary we have presented a number of arguments, from the point of view of varying speed of light theories, which could lead to neutrino superluminal behavior. In all honesty none of these are very palatable. Appealing to at least a single tachyon eigenstate might be the simplest way out. The highlight of this paper was the discovery that in such a set up, due to neutrino mixing, the flavor eigenstates need not suffer from the instabilities peculiar to tachyons, provided they are interpreted as non-linear representations of the Lorentz group and masses and mixing angles are chosen carefully.
Beyond that our paper delved into more speculative ideas (by now, however, the neutrino is expected to be crazy; see e.g. [29-34]). We may force the flavor dispersion relations we have found well beyond existing theory. In the most extreme case this would entail a cross-over from the bradyonic branch at low energies to the tachyonic branch at high energies. Then, the neutrino (either a flavor or a mass state, both options are up for grabs) starts off subluminal at low energies, but then, as its energy increases, “breaks the speed of light” to reach a maximal speed at a given finite energy. Its speed then decreases with energy, approaching the speed of light from above, as the energy goes to infinity, like any other good tachyon. As long as this is interpreted within the framework of non-linear representations of the Lorentz group, causality violations are not necessarily implied, since one should employ the associated non-linear Lorentz transformations [35,36]. It is a far-fetched idea, but extreme circumstances call for extreme measures.
We also showed how invoking Planck scale physics (and its habit of speeding up light) would imply a ridiculously low Planck energy scale, as well as the embarrassing question: why the neutrino and not other particles? We suggested a possible solution to the first problem by simply accepting the second. With a set of dispersion relations specifically tailored for the neutrino, we were able to prove that the observed effect could be predicted with a standard Planck scale. Central to the argument is the fact that whilst the energy of the neutrino beam is unexceptional, its gamma factor is very large. By putting the neutrino mass into the expression for the deformed dispersion relations we can then put this fact to good use and predict a velocity  above the speed of light for the meagre
above the speed of light for the meagre , whilst keeping the Planck scale
, whilst keeping the Planck scale .
.
We could have gone further, elaborating on the important point made in the last paragraph. We note that until recently, Ultra-High-Energy cosmic rays held the record for the largest gamma factor:
 (31)
(31)
Even for a neutrino mass state with  this would have been achieved in OPERA, with the lowest mass states definitely improving on the mark. With MINOS [37] and OPERA we are finally probing:
this would have been achieved in OPERA, with the lowest mass states definitely improving on the mark. With MINOS [37] and OPERA we are finally probing:
 (32)
(32)
Therefore, even though the energy scales in OPERA are unexceptional, something is unique. Had the neutrino been well behaved, this would have been the closest we ever got to the speed of light, without actually sitting on it. Instead the neutrino broke the speed of light barrier. In a separate paper, we propose a theory building on this fact. The basic idea is that one may extend the non-linear representations of the Lorentz group developed in [15,16] with a construction where the angle  in Lorentz transformations is replaced by a new
in Lorentz transformations is replaced by a new , saturating at a given gamma factor. We stress that, since the Lorentz group is non-compact, its experimental testing is necessarily open-ended.
, saturating at a given gamma factor. We stress that, since the Lorentz group is non-compact, its experimental testing is necessarily open-ended.
An obvious concern (for theorists and experimentalists alike) is consistency with other observations, namely SN1987A (e.g. [8,38]). Our theoretical considerations are very much at the level of toy models, so we cannot offer a detailed examination. Nonetheless we close by presenting some thoughts. Face value our first model (a tachyonic mass state) contradicts SN1987A. If one adopts the view that the mass states, rather than the flavor states, are what “moves” independently in vacuum, and postulates that one of them is tachyonic, then there should have been a tachyonic signal from SN1987A arriving 3 - 4 years earlier. However, the matter is far from clear cut. Firstly, how sure are we that such a “premonitory” burst didn’t arrive? Then, assuming the experiments were up and running [39], could we arrange for a scenario where we could reasonably have missed this early burst? The answer hinges on a crucial detail. The SN1987A are mainly electron neutrinos whereas those at OPERA are muonic neutrinos. Suppose the mixing of the former with the tachyonic state is negligible, unlike the latter. Then some tachyonic signal from SN1987A would have arrived, but it could have been negligible. Even though there are muon and tauon neutrinos among the thermal neutrinos, these are a minority, and the signal arriving 3 or 4 years ahead could easily have passed unnoticed.
The same argument can be adapted to our third model. Deformed dispersion relations should in principle apply to mass states (although the idea may be combined with a stronger “individuality” for flavors). One could therefore design a theory (either with very different masses, or with different  for the different mass states) where the proposed mechanism for speeding up neutrinos is much stronger for one mass state than the others. Requiring a low mixing with electron neutrinos would then suppress the faster than light signal from SN1987A. Some thermal muon and tauon neutrinos are produced (and most of the observed neutrinos come from this pool), but the statistics aren’t good enough to rule out a tachyonic signal from them. At any rate, we stress that the argument on thermal neutrinos results from computer simulations, not observations, and these would have to be revised, for consistency, should deformed dispersion relation affect at least one state.
for the different mass states) where the proposed mechanism for speeding up neutrinos is much stronger for one mass state than the others. Requiring a low mixing with electron neutrinos would then suppress the faster than light signal from SN1987A. Some thermal muon and tauon neutrinos are produced (and most of the observed neutrinos come from this pool), but the statistics aren’t good enough to rule out a tachyonic signal from them. At any rate, we stress that the argument on thermal neutrinos results from computer simulations, not observations, and these would have to be revised, for consistency, should deformed dispersion relation affect at least one state.
As for our second model, it actually predicts that tachyonic behaviour should not be seen in the SN1987A. All that needs to be done is for the cross-over from bradyonic to tachyonic branch to happen above 10 MeV. This is similar in spirit to one of the proposals in [8].
The most conservative explanation of OPERA, of course, remains to dismiss the the results as an “experimental error”, the ultimate bail out of the theorist. At the end of the day it is up to experimentalists to sort out their wares. We wait for an independent experiment with bated breath.
2. Acknowledgements
I’d like to thank J. Halliwell, L. Lyons, J. Sedgbeer and D. Wark for discussions.
NOTES