Towards a Mathematical Model for Elastic Wave Propagation in Granular Materials ()
1. Introduction
Granular materials consist of a collection of discrete macroscopic solid particles interacting via repulsive contact forces. Perhaps the simplest example of such a system is a dense packing of spherical glass beads under hydrostatic confining pressure. Such model systems are a useful starting point in the description of composite materials. Their physical behaviour involves complex nonlinear phenomena, such as non equilibrium configurations, energy dissipation and nonlinear elastic response [1]. We know from classical continuum dynamics that when a deformable body is under the action of a force distributed over its surface, the force is transmitted to every point inside the body [2]. Conversely, when we deal with a static packing of granular particles, the way by which the forces are transmitted within the packing remains a complex, and still unresolved, problem [3]. Several features of granular matter may be responsible for the complexity of the response to external perturbations. One important aspect lies on the observation that force networks form the skeleton that carries most of the load in a static granular medium [4]. The mechanical response of granular packings to external perturbations plays a major role in numerous engineering endeavours (such as soil mechanics and geophysics), as well as in industry (oil exploration, structural stability, product formulation in pharmacology and domestics, granular composites, heterogeneous materials, etc.).
Most laboratory experiments have been carried out using two-dimensional packings, consisting of photoelastic (i.e., birefringent under strain) disks, which have then allowed for a finest visualization of the generation and dynamical evolution of force chains. However, real granular materials are optically opaque, the photoelastic technique becomes difficult to practice. On the other hand, new tools such as pulsed ultrasonic transmission through granular beds under confined stress have been recently deviced to understand the elastic response of three-dimensional granular packings [5-7]. In particular, by studying the low-amplitude coherent wave propagation and multiple ultrasound scattering, it is possible to infer many fundamental properties of granular materials such as elastic constants and dissipation mechanisms [8].
The understanding of wave motion in granular media took a major step forward with the experimental observation of the coexistence of a coherent ballistic pulse travelling through an effective contact medium and a multiply scattered signal [5]. Such a picture is confirmed by the experiments of sound propagation in two dimensional regular lattice of spheres under isotropic compression [9], where the transmitted coherent signal remains almost unchanged for different packing realizations followed by an incoherent tail which depends on the specific packing configuration, in agreement with the completely disordered three dimensional case [5,6]. Besides the sensitive configuration coda type high frequency (HF) incoherent signals, one observes a primary low frequency (LF) coherent pulse [6,9]. This coherent pulse well defined at the leading edge of the transmitted signal corresponds to an effective wave propagating ballistically at compressional velocity c ~ 1000 m/s, and frequency f ~ 70 kHz. The sensitivity of the coherent and incoherent waves to changes in packing configurations has been studied in [6]. For independent granular samples, an ensemble average of configurations can cancel scattered signals and leave only the coherent wave. From experiments [6] one can infers that the coherent pulse is a self-averaging signal and configuration insensitive, which thus probes sound propagation in an equivalent effective contact medium. Usually the elastic response of a compressed granular packing is modeled as an assembly of spherical particles, where the contact forces between them are described by the Hertz law [10]. This model predicts that the speed of sound scales as 1/6 with the confining pressure P. However, experiments [6] (3D disordered packing) and [9] (2D regular lattice) show that for moderate pressures the speed of sound scales with a non-Hertzian exponent, roughly 1/4, followed by a Hertzian one at large values of the confining pressure.
In this paper we deal with a continuum description of wave propagation in granular packings, using the nonlinear elastic model developed in Refs [11-13]. This paper is structured as follows: In Section 2 we present a concise and detailed pedagogical introduction to granular elasticity; In Section 3 we introduce the equation of motion to describe the dynamical response of a granular packing subjected to an external perturbation and it is verified that the theory is consistent with classical elasticity; In Section 4 we solve the equation of motion for time-harmonic plane wave propagation under hydrostatic compression. Then, we derive a mathematical expression for the longitudinal wave speed with pressure dependence. In Section 5 we summarize the relevant conclusions.
2. Granular Elasticity
A basis for the construction of a theory for elastic wave propagation in granular media is provided by the elastic theory conveniently modified to account in infinitesimal forces due to force-dependent internal contacts between grains. The goal of this section is to introduce the granular elastic theory proposed by Jiang and Liu [11,12], which emphasizes the role of intrinsic features of granular dynamics such as volume dilatancy, mechanical yield and anisotropies in the stress distribution. Another fundamental ingredient is that the theory takes into account a general form of the type of contacts between the grains. On the other hand, the formulation directly extends the Boussinesq modified theory of elasticity and removes their thermodynamic inconsistency via a correct formulation of the strain free energy functional. In addition, under certain limits the theory includes the wellknown linear elasticity of isotropic and homogeneous elastic solids.
We begin with the basic notions used in the construction of a self-contained elastic theory for granular materials. To illustrate how a granular packing can be described by an elastic approach, we make the following assumptions:
• As a very first rule, we impose that the theory we will build should be invariant with respect to any Galilean transformation, i.e., any translation or rotation or combination of both, added to the displacement field of the medium should neither change their energy, nor any physical quantity we can derive from it such as the stress field.
• We do not consider the case for plastic deformations in the granular packing. Therefore, we assume that the predominant part of the energy is elastic. Elasticity implies reversible deformation, which change the internal energy ε of the deformed body according to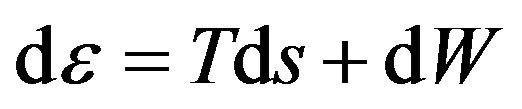 , where T is the (thermal) temperature, S is the entropy and W the work due to the force exerted on the packing. We assume a reference equilibrium state a temperature T, from which we can construct an elastic energy potential (free energy functional) F. For a static granular media the granular temperature
, where T is the (thermal) temperature, S is the entropy and W the work due to the force exerted on the packing. We assume a reference equilibrium state a temperature T, from which we can construct an elastic energy potential (free energy functional) F. For a static granular media the granular temperature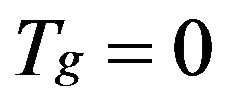 , which “measures” kinetic energy fluctuations when the system is fluidized. For a more detailed discussion and clarifications see references [11-13].
, which “measures” kinetic energy fluctuations when the system is fluidized. For a more detailed discussion and clarifications see references [11-13].
• As a mechanical model for the granular particles we consider smooth hard spheres with diameter d. We do not include friction at the contact surface between the spheres, and rotational degrees of freedom are neglected. Therefore, we consider the potential energy as a path-independent function.
• Congruently with the previous point, distributions of body or surface couples are not include in the present analysis. In this sense the present formulation is not complete and must be extended to include the effects of the grain rotation into the corresponding constitutive relations.
2.1. Continuum Theory Framework
The analysis of the deformation of a granular packing is rendered amenable to mathematical analysis by introducing the concept of a continuum medium. In this idealization it is assumed that properties averaged over a mesoscale are continuous functions of position and time. However, the presence of force chains at the grain scale, implying preferred force paths, have served as empirical argument against an isotropic continuum description of granular matter [3,4]. Nonetheless, recent findings on the stress distribution response to local and global perturbations have shed some light on the validity of using a continuum theory [14,15]. The passage from a microscopic to a macroscopic (continuum) mechanical description of granular and heterogeneous materials, including the mesoscopic disorder, has been recently addressed by Goldenberg and Goldhirsch [16-19]. They showed that exact continuum forms of the balance equations (for mass, momentum and energy) can be established as relations between spatially-weighted sums, in which a physical quantity 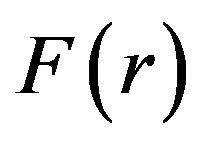 is approximated by the summation interpolant
is approximated by the summation interpolant , where
, where 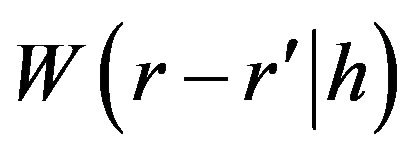 is a smooth (differentiable) function, commonly referred as the interpolating kernel, and h is the smoothing (coarse-graining) length, which determines the spatial resolution and the scales for the spatial averages. These findings justify the continuum analysis adopted in the present work. In passing, we note that the approach followed in references [16-19] seems to be congruent with the Smoothed Particle Hydrodynamics (SPH) computational method; a meshfree particle method based on Lagrangian formulation, which has been widely applied to different areas in engineering and science [20].
is a smooth (differentiable) function, commonly referred as the interpolating kernel, and h is the smoothing (coarse-graining) length, which determines the spatial resolution and the scales for the spatial averages. These findings justify the continuum analysis adopted in the present work. In passing, we note that the approach followed in references [16-19] seems to be congruent with the Smoothed Particle Hydrodynamics (SPH) computational method; a meshfree particle method based on Lagrangian formulation, which has been widely applied to different areas in engineering and science [20].
2.2. Deformation: Displacements and Strains
The displacement field inside the granular packing will be characterized by a vector field u(r). Moreover, we require that the theory starts with assumption of small deformations, i.e., for an infinitesimal deformation the displacements field and their gradients are small compared to unity . This choice limit the range of applicability of the theory but is physically reasonable for granular systems under strong static compression and small amplitude wave motion. However, the present model could provides the theoretical basis for analysis of ultrasonic wave propagation in geotechnical engineering, soil mechanics and rock mechanics.
. This choice limit the range of applicability of the theory but is physically reasonable for granular systems under strong static compression and small amplitude wave motion. However, the present model could provides the theoretical basis for analysis of ultrasonic wave propagation in geotechnical engineering, soil mechanics and rock mechanics.
To comply with the requirement of translational invariance, we express the elastic energy of the granular packing as a function of the derivatives of the displacement field. Since the displacement is a vector field, the gradient is a second order tensor whose components i; j can be written . We can split the gradient into a symmetric and antisymmetric tensor. The later will contain the rotational part of the field. Because of invariance under rotations, we require that the energy should not depend on the antisymmetric part of the gradient of displacement. On the other hand, the displacement associated with deforming the grains, stores energy reversible and maintains a static strain. Sliding and rolling lead to irreversible, plastic process that only heat up the system. So, the total strain tensor
. We can split the gradient into a symmetric and antisymmetric tensor. The later will contain the rotational part of the field. Because of invariance under rotations, we require that the energy should not depend on the antisymmetric part of the gradient of displacement. On the other hand, the displacement associated with deforming the grains, stores energy reversible and maintains a static strain. Sliding and rolling lead to irreversible, plastic process that only heat up the system. So, the total strain tensor  may be decomposed into elastic and plastic parts
may be decomposed into elastic and plastic parts . In this work we limit our analysis to granular packings under strong static compression. Therefore, the granular energy is a function of the elastic energy alone and we can neglect the plastic strain contribution. Up to linear order, the strain tensor is
. In this work we limit our analysis to granular packings under strong static compression. Therefore, the granular energy is a function of the elastic energy alone and we can neglect the plastic strain contribution. Up to linear order, the strain tensor is
 .
.
Let us remark that in the present analysis we do not include non-affine deformations. This assumption should be valid for strong compressed granular packings far from the jamming transition [21].
2.3. Strain Energy
In order to have an intrinsic form for the energy, i.e. which does not depend on the basis chosen to express the displacement field, we need to introduce only invariants of the tensor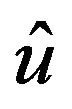 . A second order tensor in three dimensions, has only three invariants:
. A second order tensor in three dimensions, has only three invariants:
 ;
; ;
;
and .
.
Here  denotes the trace. In order to build a linear theory, we have to introduce an expression which is quadratic in the strain field. Thus only the square of the first invariant, and the second invariant, together with the assumptions of Galilean invariance and thermodynamic equilibrium, can be used and we are naturally led to the general expression of the elastic potential energy, given by the Helmholtz free energy functional [2]:
denotes the trace. In order to build a linear theory, we have to introduce an expression which is quadratic in the strain field. Thus only the square of the first invariant, and the second invariant, together with the assumptions of Galilean invariance and thermodynamic equilibrium, can be used and we are naturally led to the general expression of the elastic potential energy, given by the Helmholtz free energy functional [2]:
 where
where  and
and  are material-dependent constants which characterizes the rigidity of the solids and are called the Lamé coefficients. If
are material-dependent constants which characterizes the rigidity of the solids and are called the Lamé coefficients. If  contains only off-diagonal components, like for instance a pure shear, the elastic constant that comes into play is
contains only off-diagonal components, like for instance a pure shear, the elastic constant that comes into play is , the shear modulus. In the case of an isotropic compression,
, the shear modulus. In the case of an isotropic compression,  is proportional to the identity tensor. The elastic constant relating the pressure to the decrease of volume is now
is proportional to the identity tensor. The elastic constant relating the pressure to the decrease of volume is now 
 , the compressibility modulus. In a model for granular materials, the elastic moduli K and G must be assumed to be proportional to the volume compression
, the compressibility modulus. In a model for granular materials, the elastic moduli K and G must be assumed to be proportional to the volume compression , where
, where  is the density in the absence of external forces [11,12]. So we have
is the density in the absence of external forces [11,12]. So we have
 (1)
(1)
with  for Δ ≥ 0 and
for Δ ≥ 0 and 
 for Δ = 0, so that the elastic moduli remain finite. The exponents a and b are related to the type of contact between the grains. That is, when
for Δ = 0, so that the elastic moduli remain finite. The exponents a and b are related to the type of contact between the grains. That is, when  linear elasticity is recovered, whereas
linear elasticity is recovered, whereas  implies Hertz contacts [10]. This formulation provides a much better approximation to granular elastic behavior in which we can specify the type of contact by suitably choosing the exponents a and b. The Helmholtz free energy in the Jiang-Liu model is [11,12]:
implies Hertz contacts [10]. This formulation provides a much better approximation to granular elastic behavior in which we can specify the type of contact by suitably choosing the exponents a and b. The Helmholtz free energy in the Jiang-Liu model is [11,12]:
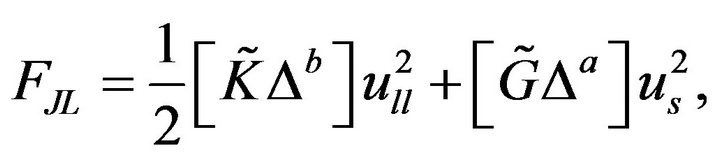 (2)
(2)
where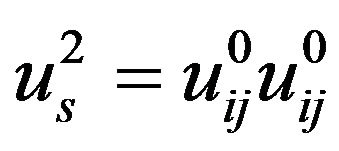 , with
, with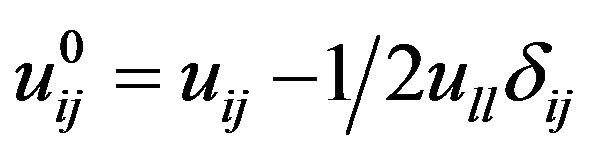 .
.
The free energy strain potential (2) is stable only in the range of strain values that keeps it convex. Therefore, Equation (2) naturally accounts for unstable configurations of the system, as the yield, which appears as a phase transition on a potential-strain diagram.
2.4. Stress Field and Equilibrium
We now introduce the conjugated field to the strain: the granular stress field. By definition, this stress field, which is also a second-order symmetric tensor field,  is related to the strain field by
is related to the strain field by
 (3)
(3)
where  is the Kronecker’s delta. Galilean invariance implies that the stress field should not do any work during a rigid motion of the solid. This property can be used to derive the balance equation satisfied by the stress field, always valid even if the rheological behaviour considered is not linear. When the granular packing is subjected to an external force density f, the balance equations read
is the Kronecker’s delta. Galilean invariance implies that the stress field should not do any work during a rigid motion of the solid. This property can be used to derive the balance equation satisfied by the stress field, always valid even if the rheological behaviour considered is not linear. When the granular packing is subjected to an external force density f, the balance equations read
 (4)
(4)
This equation have been checked in references [22,23], where the authors analyzed several features of static granular packings, such as the stress dip in sand piles, the stress distribution in silos and under point loads, and the variation with pressure of the elastic moduli.
3. Granular Elastodynamics
Now we are ready to formulate a mesoscopic elastodynamic theory for granular materials. Above we stated that the theory is founded on the assumption of a continuum (coarse grained) field description and an elastic theory for granular materials which takes into account the compression dependent elastic moduli.
Equation of Motion
We start with the equation of motion for the elastic displacement u at time t and postion r,
 (5)
(5)
From the Jiang-Liu elastic model the stress tensor (3) which, by the Hooke’s law, is given in terms of the Lamé coefficients by
 (6)
(6)
where  denotes the unitary tensor and the superindex T means transposition. Inserting Equation (6) into Equation (5) and rearranging terms, the equation of motion is
denotes the unitary tensor and the superindex T means transposition. Inserting Equation (6) into Equation (5) and rearranging terms, the equation of motion is
 (7)
(7)
this expression indicates that the elastic wave have both dilatational  and rotational deformations
and rotational deformations  . Let us remark that setting
. Let us remark that setting , as it would be for linear elasticity, Equation (7) reduces to
, as it would be for linear elasticity, Equation (7) reduces to
 (8)
(8)
The above equation further simplifies to the wellknown wave equation
 (9)
(9)
The terms  and
and  are the compressional wave speed, and shear or transverse wave speed, respectively. This proves that the present elastodynamic model includes the well-known linear elasticity of isotropic and homogeneous elastic solids.
are the compressional wave speed, and shear or transverse wave speed, respectively. This proves that the present elastodynamic model includes the well-known linear elasticity of isotropic and homogeneous elastic solids.
4. Wave Propagation
4.1. Time-Harmonic Plane Wave Propagation under Hydrostatic Compression
Now we proceed to analyze the case of time-harmonic plane wave under compression. We shall assume a perturbation of the packing by a time-harmonic plane deformation given by
 (10)
(10)
where the vector U is the amplitude of the displacement along the plane of the wave (polarization), while k is the wave vector and  is the pulsation. We will now consider the case for isotropic compression. In the unperturbed reference configuration the strain tensor is
is the pulsation. We will now consider the case for isotropic compression. In the unperturbed reference configuration the strain tensor is
 , i.e.,
, i.e.,
 (11)
(11)
and the trace is . The traceless part,
. The traceless part,  , is
, is
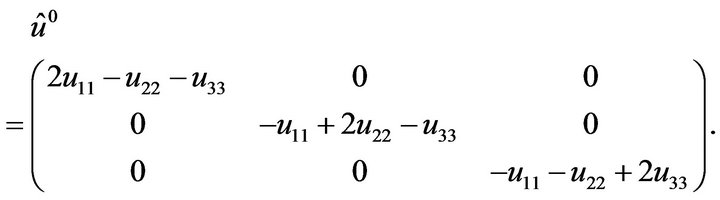 (12)
(12)
Therefore, the invariant 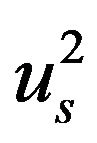 is
is
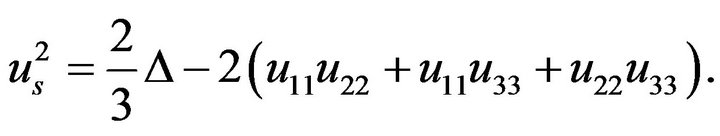 (13)
(13)
Finally, from (3) the stress tensor is
 (14)
(14)
Now we consider the displacements parallel to the wave normal plane along the  axis and amplitude
axis and amplitude 
 (15)
(15)
As a next step, we need to calculate the disturbances. Thus the strain tensor associated with the wave is
 (16)
(16)
where . The volume compression is
. The volume compression is . On the other hand, the traceless part
. On the other hand, the traceless part  is
is
 (17)
(17)
Now the invariant  is
is
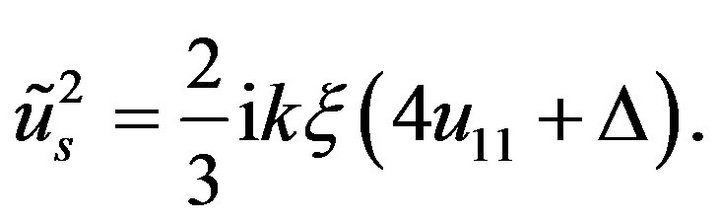 (18)
(18)
The components of the perturbed stress tensor are given by
 (19)
(19)
which in matrix notation have the diagonal form  , where
, where
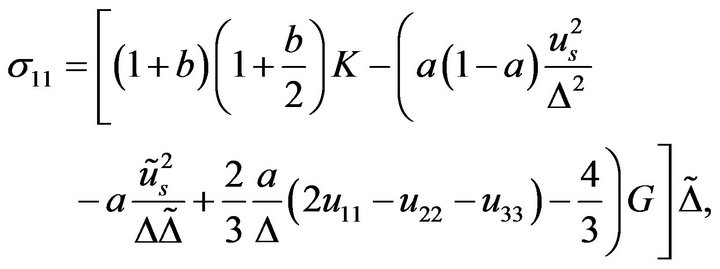 (20)
(20)
 (21)
(21)
 (22)
(22)
We can verify that . Finally, using Equation (15) and (20) we can ensemble the equation of motion to obtain
. Finally, using Equation (15) and (20) we can ensemble the equation of motion to obtain
 (23)
(23)
As we are interested in the case for isotropic compression, the components for the strain are  , thus
, thus . Therefore, the resulting equation of motion is
. Therefore, the resulting equation of motion is
 (24)
(24)
The pulsation  and the wave vector
and the wave vector  define the longitudinal wave speed, i.e.,
define the longitudinal wave speed, i.e.,
 (25)
(25)
Furthermore, noting that  and
and , the longitudinal wave speed is
, the longitudinal wave speed is
 (26)
(26)
4.2. Speed of Sound and Pressure Dependence
In Refs. [5] and [9] the dependence of  vs the applied external pressure P was analyzed. The experiments show a scaling dependence for
vs the applied external pressure P was analyzed. The experiments show a scaling dependence for  with P. In order to capture the dependence for the calculated longitudinal wave speed (26) with the pressure, we use the granular free-energy functional (2). The pressure is given by
with P. In order to capture the dependence for the calculated longitudinal wave speed (26) with the pressure, we use the granular free-energy functional (2). The pressure is given by
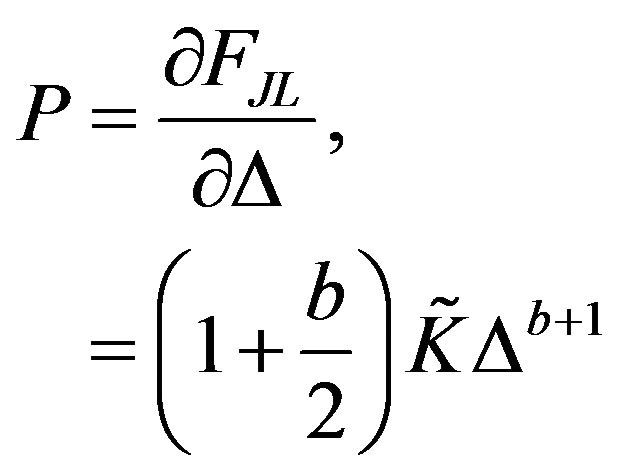 (27)
(27)
Therefore, the compression  is:
is:
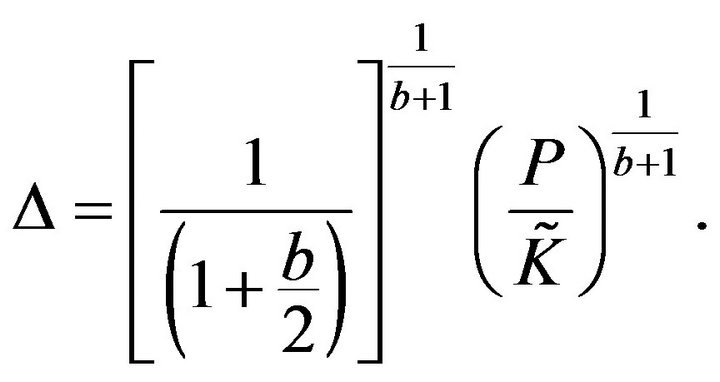 (28)
(28)
If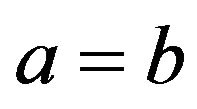 , Equation (26) can be written as
, Equation (26) can be written as
 (29)
(29)
where  is defined as
is defined as
 (30)
(30)
The present theoretical analysis, let us to conclude that the longitudinal wave speed scales with the pressure as
 (31)
(31)
where  is given by the mechanics of the contact model.
is given by the mechanics of the contact model.
According to experiments [5] and [9] we have the following two cases:
For  (Hertzian contacts):
(Hertzian contacts):
 (32)
(32)
For  (non-Hertzian contacts):
(non-Hertzian contacts):
 (33)
(33)
Equations (32) and (33) behave according to the experiments in a qualitative manner. In Figure 1 we compare the above equations with the data reported in [5].

Figure 1. Velocity sound speed vp (data points [5]) of the coherent wave versus the applied stress P. Red line: b = 1/2 (Hertzian contacts) with  = 7.9; Green dashed line: b = 1 with
= 7.9; Green dashed line: b = 1 with  = 4.9.
= 4.9.
However, at this point we have not a criterium to understand why the velocity “changes” with  between Equations (32) and (33), i.e., from the non-Hertzian contact model
between Equations (32) and (33), i.e., from the non-Hertzian contact model  (33) for moderate pressures, to the Hertzian contact model
(33) for moderate pressures, to the Hertzian contact model  (32) for higher pressures.
(32) for higher pressures.
From the experimental data one can characterize the pressure dependence of the sound velocity introducing an effective exponent defined by the logarithmic derivative between  and
and 
 (34)
(34)
The compression  clearly influences the behavior of the velocity because it depends on the pressure. From Equation (29) we can estimate the dependence on
clearly influences the behavior of the velocity because it depends on the pressure. From Equation (29) we can estimate the dependence on  as
as
 (35)
(35)
The qualitative behavior of  can be obtained by interpolating from the asymptotic behavior at large and moderate pressures. This opens the question about if one can assume that
can be obtained by interpolating from the asymptotic behavior at large and moderate pressures. This opens the question about if one can assume that 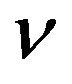 is continuos, monotonically decreasing function from
is continuos, monotonically decreasing function from  to
to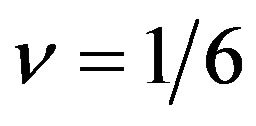 , while
, while  increases. Or if it corresponds to discontinuous transition between the exponents.
increases. Or if it corresponds to discontinuous transition between the exponents.
Now we are in position to relate the parameter  and the exponent
and the exponent . We can estimate that
. We can estimate that 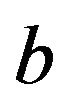 behaves according to the effective exponent
behaves according to the effective exponent  as
as
 (36)
(36)
Verifying from the experiments, that the high pressure limit , implies for our model that
, implies for our model that . While for moderate pressures
. While for moderate pressures . The first case clearly corresponds to the Hertz contact model in the Jiang-Liu theory. The resistance to an external compression by a granular packing is due macroscopic rigidity mediated by the small contact regions between the grains and the contact areas increase with pressure. For spheroidal objects the Hertz model implies that the amount of deformation
. The first case clearly corresponds to the Hertz contact model in the Jiang-Liu theory. The resistance to an external compression by a granular packing is due macroscopic rigidity mediated by the small contact regions between the grains and the contact areas increase with pressure. For spheroidal objects the Hertz model implies that the amount of deformation  increases with
increases with  as
as  and the elastic energy
and the elastic energy  of the deformed sphere behave as
of the deformed sphere behave as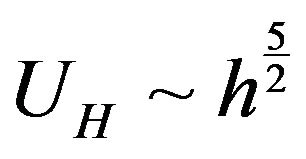 . This corresponds to the scaling at the high pressure regime. Various interpretations have been proposed for non-Hertzian contacts (e.g., [24,25]). However, let us remark that in 1971 Johnson, Kendal and Roberts [26] quoted some experimental outcomes where for moderated loads contacts areas between the bodies were considerably larger than those predicted by the Hertz model, while for high loads the results closely fitted the Hertz theory. Their observation is congruent with the scaling transition reported in [5] and [9]. The JKR theory [26] introduces the effects due to the energy at the surfaces of the contact bodies. According to [26], at moderate pressures tensile forces are present at the deformed surface modifying the Hertz contact law. They proposed that the tensile forces act as an attractive surface force even for clean and dry surfaces. These surfaces forces are of little significance at high loads, but become more significative as the pressure is reduced.
. This corresponds to the scaling at the high pressure regime. Various interpretations have been proposed for non-Hertzian contacts (e.g., [24,25]). However, let us remark that in 1971 Johnson, Kendal and Roberts [26] quoted some experimental outcomes where for moderated loads contacts areas between the bodies were considerably larger than those predicted by the Hertz model, while for high loads the results closely fitted the Hertz theory. Their observation is congruent with the scaling transition reported in [5] and [9]. The JKR theory [26] introduces the effects due to the energy at the surfaces of the contact bodies. According to [26], at moderate pressures tensile forces are present at the deformed surface modifying the Hertz contact law. They proposed that the tensile forces act as an attractive surface force even for clean and dry surfaces. These surfaces forces are of little significance at high loads, but become more significative as the pressure is reduced.
5. Conclusions
In this paper, we have shown that the nonlinear elastic theory proposed by Jiang and Liu [11] can be used to derive a time-evolution equation for the displacement field. The present formulation naturally accounts for features that are intrinsic to the dynamics of granular matter, considering microstructure information through the type of contact between the grains. The theory shows that the wave speed scales with pressure as . From the experimental data we have introduced the effective exponent
. From the experimental data we have introduced the effective exponent  and their relationship with the parameter
and their relationship with the parameter . This was done to characterize the transition from the non-Herztian regime
. This was done to characterize the transition from the non-Herztian regime  to the Herztian regime
to the Herztian regime . However, we can not conclude if
. However, we can not conclude if  is a continuos, monotonically decreasing function of
is a continuos, monotonically decreasing function of , or a discontinuous transition at some critical value of
, or a discontinuous transition at some critical value of  given by the intersection between Equations (32) and (33). On the other hand, we have provided an interpretation for the non-Hertzian contacts based on the JKR theory [26]. We hope that the present theoretical findings will stimulate further experimental works to explore in detail the behavior of contact deformations under compression and the effects on wave propagation in granular materials.
given by the intersection between Equations (32) and (33). On the other hand, we have provided an interpretation for the non-Hertzian contacts based on the JKR theory [26]. We hope that the present theoretical findings will stimulate further experimental works to explore in detail the behavior of contact deformations under compression and the effects on wave propagation in granular materials.
The mathematical model reported here is a first step towards the implementation and validation of computational engineering simulations for a variety of problems related to elastic wave propagation in granular composites. The equations of motion (7) are three partial differential equations which can be solved numerically for ,
,  and
and  provided with appropriate boundary and initial conditions, as for example using finite-element codes. In addition, the mathematical formulation at hand could help to inspire new ideas towards the construction of working theories for granular media, which may ultimately improve our interpretation of present experiments. For instance, understanding how waves do actually propagate in heterogeneous media is relevant to well-known problems such as earthquakes and seismic wave propagation and reflection in order to estimate the hydrocarbon content of potential oil wells.
provided with appropriate boundary and initial conditions, as for example using finite-element codes. In addition, the mathematical formulation at hand could help to inspire new ideas towards the construction of working theories for granular media, which may ultimately improve our interpretation of present experiments. For instance, understanding how waves do actually propagate in heterogeneous media is relevant to well-known problems such as earthquakes and seismic wave propagation and reflection in order to estimate the hydrocarbon content of potential oil wells.
NOTES