Effect of the Weaving Density of Aramid Fabrics on Their Resistance to Ballistic Impacts ()
1. Introduction
Aramid [poly(p-phenylene terephthalamide), PPTA] consists of relatively rigid polymer chains with linked benzene rings and amide bonds. This structure affords aramid fibers high tenacity, high modulus, and toughness [1-3]. Based on these merits, aramid fibers are used as ballistic materials. Figure 1 represents the chemical structure of aramid fibers.
Generally, ballistic materials can be divided into hard and soft armors [4-7]. Unlike traditional structural composites, hard armors, also known as armor-grade composites, contain only 20% by weight matrix and are made to readily delaminate. Conversely, soft armors consist of multilayered, woven textiles and are used to protect against various types of bullets.
The ability of a woven fabric to protect against bullets depends primarily on the mechanical properties of the yarn such as tenacity, tensile modulus, and toughness. However, Laible [8] demonstrated that “the relationship between the mechanical properties of a yarn and the ballistic resistance of a plied fabric from such yarn has never been established.” In other words, other factors exist that may influence ballistic performance.
Generally, the energy absorption mechanism of a fabric armor depends on several additional factors such as the weave pattern, the number of fabric plies, and weave density. Weave patterns used in ballistic applications are usually plain and basket weaves. Fabrics with unbalanced weaves typically yield inferior ballistic performance [9]. Lim et al. [10] investigated ballistic impacts on multiply systems to characterize the reinforcement effect of multiple layers. They concluded that inter-ply friction inhibited the sideways motion of the yarns, resulting in an increased resistance to ballistic penetration. Weave density, which refers to the number of yarns per unit dimension along the principal yarn directions, affects the areal density of the fabric and the crimp. Shockey et al. [11] concluded that the energy absorbed by a fabric was proportional to the fabric’s areal density. Yarn crimp refers to the degree of yarn undulation and is a property of the weave. Tan et al. [12] compared two methods of modeling crimp using empirical results. They concluded that accounting for crimp by modeling the linear elements in a zigzag manner yielded more accurate results than trying to account for crimp as a constitutive property.
However, little has been reported regarding correlations between ballistic properties and the weave pattern of aramid woven fabrics. Furthermore, a comparative study of ballistic performance has not been carried out that accounts for both fabric properties and individual yarn properties. In the current study, two types of aramid
Figure 1. The chemical structure of aramid fibers.
woven fabrics, each with a different weave density, were prepared, and the influence of weave density on their fabric properties and ballistic behavior were ascertained. This study provides fundamental information on how weave density regulates fabric properties and the ballistic behavior of aramid woven fabrics.
2. Experimental
2.1. Materials
Aramid fibers (trademark Heracron®) were produced by Kolon Inc. (Kwach’on, Korea) with a fiber fineness of 600 denier. Table 1 shows some of the basic properties of Heracron® filament fibers, each composed of 665 mono-fibers. Two types of Heracron® fabrics, HT600-1 and HT600-2, were woven for ballistic tests; the physical characteristics of these fabrics are given in Table 2. While the two fabrics had the same weave structure and fiber fineness, the weaving densities were different. Relative to HT600-2, HT600-1 was woven using more weft fiber, resulting in a much higher areal density. Detailed fabric properties are discussed below.
2.2. Analysis
Filament fiber tests were performed in accordance with ASTM Standard D2256-97(ASTM 2000). Each fiber specimen had an initial length of 50 cm. At the start of the test, the middle 25 cm of the fiber spanned between the instrument grips. The crosshead separation rate was maintained at 2 mm/s and the specimen was elongated until rupture. All of the specimens were twisted at a rate of 1.2 turns/cm. The data from 20 independent measurements are expressed as an average with a single standard deviation.
Fabric tests were performed in accordance with ISO 13934-1. All sample fabrics were created from the HT600 fabrics using the ravel strip method. Each sample had an initial length of 1.2 m and a width of 50 cm. A 50 mm length at each end of each sample was clamped into

Table 1. Physical properties of Heracron® filament fibers.

Table 2. Heracron® fabric (HT600) specifications.
a constant grip. The sample was then wrapped twice around each constant grip. During each test, the load frame crosshead moved at constant rate of 2 mm/s. Samples were pulled until rupture. Twelve samples in total were tested. Six were elongated along the warp, with the weft running along the width. The other six were elongated along the weft, with the warp running along the fabric width. The percent crimp, as defined by ISO 7211- 3, was calculated as k = [(P – L)/L] × 100%, where L is the distance between two ends of the projection of a yarn onto the plane of the fabric and P is the actual length of the yarn.
Ballistic shooting tests were performed on 34-ply samples of each of the two fabrics (HT600-1 and HT600- 2) in accordance with NIJ Standard-0101.06, “Ballistic Resistance of Body Armor, Level 3A Methods.” Tests were performed with 44 Magnum semi-jacketed hollow point (SJHP) bullets with a mass of 15.6 g (240 g) impacted at a velocity of 436 ± 9 m/s (1430 ± 30 ft/s). Six bullets were shot into each sample. After shooting, the depth of the puncture and the back deformation signature (BFS) formed on the backing material were measured. All tests were conducted at H.P. White Laboratory, Inc. (Street, MD, USA).
3 Result and Discussion
3.1. Fiber and Fabric Property
Table 3 summarizes the physical properties of the HT600-1 and HT600-2 fabrics. The thickness of HT600- 1 was greater that that of HT600-2, but the fabric tensile strength, generally considered the most important fabric property, showed unusual characteristics. HT600-1 was stronger than HT600-2 along the weft, which is reasonable since HT600-1 was woven using more weft fiber, as described in the Experimental section. However, HT600- 2 boasts a higher tensile strength along the warp despite having the same warp yarn number as HT600-1.
This indicates that the fabric tensile strength is not a simple function of weaving density alone. Generally, yarn crimp refers to the degree of yarn undulation due to interlacing in the woven structure. In a plain weave, the degree of crimp is unbalanced; the warp yarns are typically more crimped than the weft. As shown in Table 3, the warp crimps of HT600-1 and HT600-2 were 4.10% and 2.96%, respectively. Increasing yarn crimp in a particular direction generally decreases fabric strength and modulus because the tensile load is initially used to de-crimp the yarn instead of extending it [13]. Thus HT600-1, which possesses a higher weft weaving density, and therefore a higher warp crimp ratio, exhibited a relatively lower tensile strength along the warp.
Individual yarn properties were investigated in detail by extracting warp and weft yarns8 from each fabric. Table 4 shows the physical properties of extracted warp and weft from Heracron® fabrics. The warp of HT600-1 exhibited the most damage relative to the other extracted yarns. Despite their high tensile strength, aramid fibers

Table 3. Physical properties of Heracron® woven fabrics.

Table 4. Physical properties of extracted warp and weft yarns from Heracron® fabrics.
consist of highly oriented and ordered crystalline polymer chains, resulting in a rigid structure that does not endure bending. This structural characteristic gives rise to limited lateral cohesion between the molecular chains, such as hydrogen bonds or van der Waals forces [14]. These findings indicate that highly crimped aramid fibers may be significantly weakened due to the innately weak bending properties of the material.
This phenomenon may also be explained by the weaving process used to generate the fabrics. A powerful beating motion is required to obtain the higher weaving density [13], which may damage and consequently weaken the yarn. Therefore, HT600-1, with its relatively denser weave, may absorb a considerable amount of damage during weaving, thereby weakening the fibers and the fabric itself.
The above data were used to calculate the dimensionless fiber property, U*, defined as the product of the specific fiber toughness and strain wave velocity, using the follow equation:
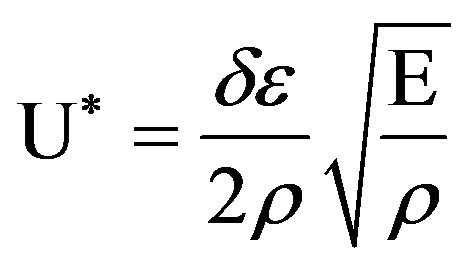
where δ is the fiber ultimate tensile strength, ε is the fiber ultimate tensile strain, E is the Young’s modulus, and ρ is fiber density. U* can be used to qualitatively assess the performance of fibers. Calculated U* values are given in Table 4. Note that the U* values of HT600-1 were lower than those of HT600-2. Moreover, U* along the warp of HT600-1 was extremely low. Cunnif [15] demonstrated that U* may be a major factor that relates ballistic impact performance to fiber mechanical properties, independent of other parameters such as impacting projectile mass, presented area, or armor system areal density. Although the exact relationship between the mechanical properties of a yarn and the ballistic resistance of a plied fabric from such yarn has never been established, the conclusion that the mechanical properties of the yarn would affect a fabric’s ballistic characteristics seems self-evident.
3.2. Ballistic Property
A comparison of ballistic properties can usually be made by analyzing crushed bullets retrieved from the tested fabrics. An increase in bullet diameter at the same ply may be due to a lesser degree of energy propagation and dissipation by the fabric, which would indicate inferior ballistic performance. Figure 2 shows a bottom view of crushed bullets retrieved from the seventh ply the HT600 fabrics. Note that the diameter of the bullet retrieved from HT600-2 was much wider, and the degree of squash much greater, than the bullet retrieved from HT600-1, demonstrating that HT600-2 has a better energy absorp-

(a)HT600-1 (b)HT600-2
Figure 2. A bottom view of the crushed bullets retrieved from HT600 fabrics.
tion capability and significantly better ballistic properties than HT600-1.
Figure 3 shows perforated regions in the HT-600 fabrics impacted by the projectile. More yarn was broken in the HT600-1 fabric and the perforation region was larger than that of HT600-2. Upon impaction by a projectile, fabrics generally fail through perforation mechanisms, which reflect both the energy absorption capability and the ballistic performance of the fabric. An increase in the number of broken yarns and an enlargement of perforated regions may indicate that the kinetic energy of the bullet could not be absorbed by the fabric efficiently. The results reported herein show that the kinetic energy of a bullet is more efficiently dissipated in the HT600-2 fabric, resulting in ballistic properties superior to those of HT600-1.