1. Introduction
We consider optimal investment for the one-step financial model with a finite number of assets. The classical Markowitz optimization problems are looking for portfolios that either maximize the expected return for a given variance threshold, or minimize the variance for a given expected return. However, using variance as a measure of risk has a serious drawback: high profits are penalized in the same way as high losses. Instead, in what follows we shall use coherent measures of risk (cf. [1]), that provide a much better quantification of risk.
In our set-up, the space of financial positions is a vector space with vector ordering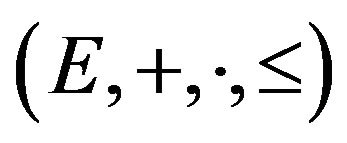 . Besides the origin 0 in E, we distinguish a (strictly positive) reference cash stream denoted by 1. In the space of linear price systems
. Besides the origin 0 in E, we distinguish a (strictly positive) reference cash stream denoted by 1. In the space of linear price systems , i.e., the algebraic dual of
, i.e., the algebraic dual of , we fix a total subspace
, we fix a total subspace  (i.e., if
(i.e., if  for all
for all , then
, then ) and consider the weak*-topology on
) and consider the weak*-topology on  associated to the dual pair
associated to the dual pair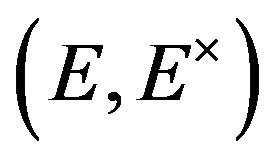 .
.
A coherent measure of risk (see [2]) is a real valued mapping  defined on
defined on  which is subadditive:
which is subadditive:
 for
for , positive homogeneous:
, positive homogeneous:  for
for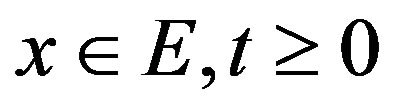 , monotonic:
, monotonic:
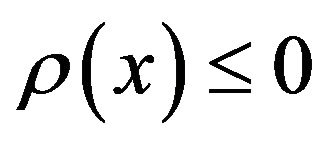 if
if , and translation invariant:
, and translation invariant:
 for
for  and any real
and any real .
.
The following property will be needed in our results. A coherent measure of risk  is called continuous from below (cf. [1,3]) if
is called continuous from below (cf. [1,3]) if 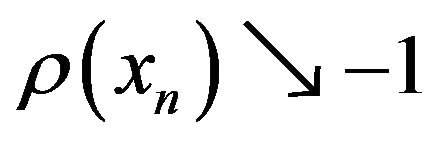 for any sequence
for any sequence
 in
in  satisfying
satisfying . Note that, if
. Note that, if 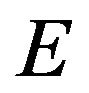
has a strong order unit, continuity from below is equivalent to the more familiar condition:  provided
provided  (see [3,4]).
(see [3,4]).
2. Main Results
Our first result formulates and solves in our set-up the first Markowitz problem, i.e., the so-called “agentindependent optimization problem”: find portfolios that maximize the expected return for a given (measure of) risk. Particular cases have been considered in [5-8].
Theorem 1. Let 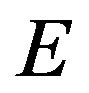 be an ordered locally convex vector space, and
be an ordered locally convex vector space, and  a total Banach subspace of
a total Banach subspace of . Let
. Let and
and  be fixed; if
be fixed; if  is a coherent measure of risk continuous from below, then the following optimization problem:
is a coherent measure of risk continuous from below, then the following optimization problem:
 (1)
(1)
admits optimal solutions.
Proof. According to the structure theorem for coherent measures of risk (see e.g. [3], Theorem 2.1),  admits the following representation
admits the following representation
 (2)
(2)
for some weak*-closed convex set , in which all
, in which all  are positive (i.e.,
are positive (i.e.,  for
for ) and normalized (i.e.,
) and normalized (i.e., ). Note that continuity from below of
). Note that continuity from below of  implies continuity in the order convergence topology of all
implies continuity in the order convergence topology of all  in formula (2), see [3].
in formula (2), see [3].
Let us define

where the bar denotes closure. By the continuity from below of  and the Krein-Šmulian theorem (see e.g. [9]), the set
and the Krein-Šmulian theorem (see e.g. [9]), the set  is weak*-compact, hence
is weak*-compact, hence  is compact. Therefore, using (2), the definition of
is compact. Therefore, using (2), the definition of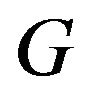 , continuity from below of
, continuity from below of  and James’ theorem (see [9]), we obtain for any
and James’ theorem (see [9]), we obtain for any :
:

In particular the sup in (2) is achieved, and for any  one has
one has
 (3)
(3)
where the threshold  is given in formula (1).
is given in formula (1).
As  for
for , from (2) it follows that, for some
, from (2) it follows that, for some , one has
, one has  for
for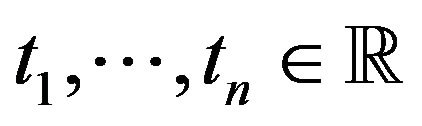 . Take
. Take  in the latter and, using linearity, obtain
in the latter and, using linearity, obtain , i.e.,
, i.e., . Similarly obtain
. Similarly obtain . This means
. This means , hence the following is well defined:
, hence the following is well defined:
 (4)
(4)
Then the max value in (1) equals 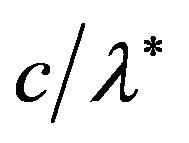 and is achieved at every
and is achieved at every  satisfying:
satisfying:
 (5)
(5)
Indeed, if  for some
for some
 , take
, take  satisfying
satisfying

Condition (3) and definition (4) imply that
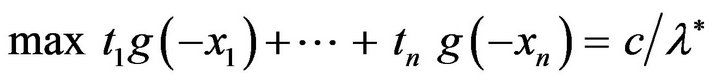 and the max is achieved at every
and the max is achieved at every 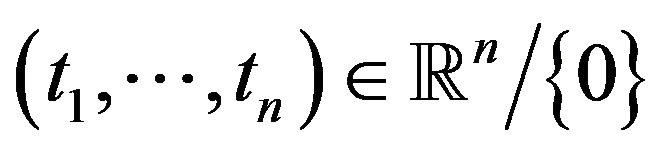 satisfying condition (5). □
satisfying condition (5). □
Problem (1) is for investing a sum of money in securities; it is possible that the investor already possesses a capital with terminal value , in which case minimizing the risk leads to the second Markowitz optimization problem, or “single-agent optimization problem”. Alternatively, one can seek the minimum price which allows us to sell a payment order, and then compile a hedging portfolio of assets such that the risk of the entire operation will be negative or zero. Our second result formulates and solves the second Markowitz problem in our set-up.
, in which case minimizing the risk leads to the second Markowitz optimization problem, or “single-agent optimization problem”. Alternatively, one can seek the minimum price which allows us to sell a payment order, and then compile a hedging portfolio of assets such that the risk of the entire operation will be negative or zero. Our second result formulates and solves the second Markowitz problem in our set-up.
Theorem 2. Let  be an ordered locally convex vector space, and
be an ordered locally convex vector space, and 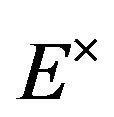 a total Banach subspace of
a total Banach subspace of . Let
. Let 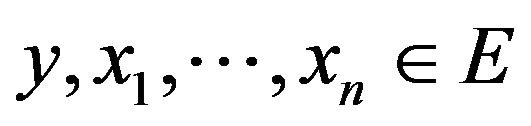 be fixed; if
be fixed; if  is a coherent measure of risk continuous from below, then the following optimization problem
is a coherent measure of risk continuous from below, then the following optimization problem
 (6)
(6)
admits optimal solutions.
Proof. Let us denote

Using a similar argument as in the proof of Theorem 1, we obtain for any :
:

In particular, for all 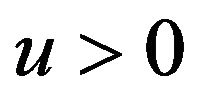 and any
and any  one has
one has
 (7)
(7)
As  for
for , using a similar argument as in the proof of Theorem 1, we obtain that the following is well defined
, using a similar argument as in the proof of Theorem 1, we obtain that the following is well defined

Then the min value in (6) is given by  and is achieved at every
and is achieved at every  satisfying:
satisfying:
 (8)
(8)
Indeed, take  satisfying
satisfying
 for some
for some .
.
Condition (7) and definition (8) imply that
 and the min is achieved at every
and the min is achieved at every  satisfying condition (9). □
satisfying condition (9). □
3. Applications
Examples. 1) We can solve explicitly problems (1) and (6) in the important case of Tail VaR (short for Tail Value at Risk). More precisely, consider  and define the Tail VaR of order
and define the Tail VaR of order  as the coherent measure of risk with the representation (2) in which
as the coherent measure of risk with the representation (2) in which , cf. [1,3,10]. One can easily check that Tail VaR is continuous from below. More, Tail VaR is one of the best coherent risk measures, because is the smallest law invariant coherent risk measure that dominates the Value of Risk (cf. [3,11]). In the context of Theorem 1, we have that
, cf. [1,3,10]. One can easily check that Tail VaR is continuous from below. More, Tail VaR is one of the best coherent risk measures, because is the smallest law invariant coherent risk measure that dominates the Value of Risk (cf. [3,11]). In the context of Theorem 1, we have that

has the optimal solution equal to . Indeed, one can easily check that
. Indeed, one can easily check that  and any positive constant multiple of
and any positive constant multiple of  is an optimal solution of (1). In the context of Theorem 2, we have that
is an optimal solution of (1). In the context of Theorem 2, we have that

has the optimal solution equal to Tail VaR . Indeed, one can check that
. Indeed, one can check that  Tail VaR
Tail VaR because
because  is an optimal solution of (6). This situation occurs in problems (1) and (6) for complete models, such as Black-Scholes and Cox-Ross-Rubinstein.
is an optimal solution of (6). This situation occurs in problems (1) and (6) for complete models, such as Black-Scholes and Cox-Ross-Rubinstein.
2) Recall that a coherent measure of risk identifies unacceptable positions, i.e. with strictly positive risk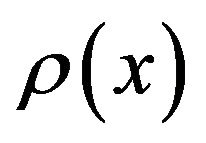 . A good measure of the latter are the so-called relevant measures of risk: given
. A good measure of the latter are the so-called relevant measures of risk: given , a coherent measure of risk
, a coherent measure of risk  is called g-relevant (cf. [1,3,10]) if
is called g-relevant (cf. [1,3,10]) if  and
and  imply
imply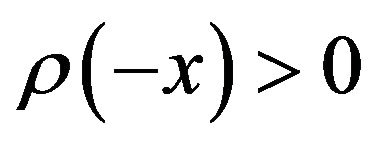 .
.
Let us consider ; we have
; we have 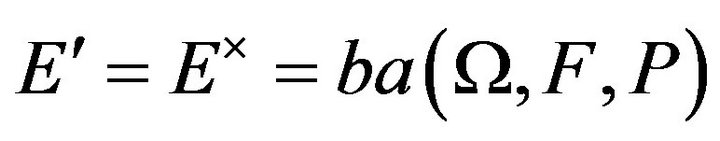 , the Banach space of bounded finitely additive measures on F and absolutely continuous with respect to P. In this case, all functionals
, the Banach space of bounded finitely additive measures on F and absolutely continuous with respect to P. In this case, all functionals  (given by formula (2) above) describing a coherent measure of risk continuous from below and
(given by formula (2) above) describing a coherent measure of risk continuous from below and  -relevant are genuine (i.e.,
-relevant are genuine (i.e.,  -additive) probability measures equivalent to
-additive) probability measures equivalent to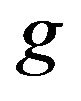 . The particular case
. The particular case , i.e., g represents integration with respect to
, i.e., g represents integration with respect to , has been treated in [2], Theorem 3.4, and the associated optimization problems (1) and (6) have been completely solved in [8,12] (see also [4]).
, has been treated in [2], Theorem 3.4, and the associated optimization problems (1) and (6) have been completely solved in [8,12] (see also [4]).
The research of George Stoica was partially supported by a grant from the Natural Sciences and Engineering Research Council of Canada.