Voltage Control in Smart Grids: An Approach Based on Sensitivity Theory ()
1. Introduction
Due to the development of Distributed Generation (DG), which is installed in Medium-Voltage Distribution Networks (MVDNs) such as generators based on renewable energy (e.g., wind energy or solar energy), voltage control is currently a very important issue.
The voltage of MVDNs is now regulated acting only on the On-Load Tap Changer (OLTC) of the HV/MV transformer [1]. The OLTC control is typically based on the compound technique, and this method does not guarantee the correct voltage value in the network nodes when the generators deliver their power [2,3].
When a generator injects power in the network, the voltage tends to rise. In HV networks this phenomenon happens mainly when reactive power is injected, because the resistance is negligible if compared with the inductive reactance [4]. Instead in MVDNs the resistance is not negligible and the result is that an injection of active power also increases the voltage.
In other words the so-called Pq - QV decoupling [5], which is a typical of HV networks, is inexistent in MVDNs. The P variations are “coupled” with the voltage variations.
If no precautions are taken, in particular network conditions the overcome of the maximum admissible voltage can happen in any nodes.
When a generator injects power, the voltage rises in all network nodes, but some nodes are mainly influenced than others by the power injection. This influence can be obtained using a Sensitivity method.
In this paper an approach based on Sensitivity Theory is shown, in order to control the network voltage using the reactive power exchanged between network and the distributed generators. This approach allows to control the voltage in the long term period. Besides, fastdynamic voltage disturbances are not taken into account [6].
After the theoretical analysis, a numerical example is shown, in order to validate the proposed theory.
The proposed method differs from the others used in HV networks analysis, based on the Jacobian Matrix [1,2-4] and its application is easy.
The topological proprieties that results from the theoretical analysis imply that the proposed sensitivity method can be easily implemented in automatic voltage control devices, in order to obtain the distributed voltage regulation.
The automatic voltage regulation in a distributed manner is a typical topic of the Smart Grids context.
The paper is structured in the following way. In Section 1, the proposed voltage control method is shown, and an overview on the voltage profiles with DG, are given. In Section 3, the proposed Sensitivity approach is studied, referring to a MV test network, composed by four nodes. Finally, in Section 4, a numerical application is presented, in order to validate the proposed theory.
2. The Proposed Criteria to Control the Network Voltage with Distributed Generation
Many methods can be used to control the voltage in network nodes (network voltages). The proposed method varies the reactive power exchanged between the generators and the network while maintaining the OL-TC in a fixed position for a particular load condition.
Let us suppose that the Automatic Voltage Regulator (AVR) that controls the OLTC maintains the MV bus-bar voltage at the rated value (1 p.u.), assuming that the transformer taps are adequate.
For passive grids, when no generators are connected to the MVDN, the voltage profile (VP; i.e., the voltage values along a line) decreases monotonically (see profile a in Figure 1) due to the load absorptions. When the generators are connected and inject power into the MVDN, the nodal voltages increase and the VP is no longer monotonic, as shown in profile b in Figure 1 (profile b). This phenomenon also occurs if generators work at unitary power factor (i.e., only active power is injected due to the non-negligible network resistance) [7].
It is important to note that, in steady-state, the condition maintained at the MV busbar by the AVR decouples the MV feeders, and the result is that each feeder works without the influence of the other lines. In other words, the loads and generators connected to other feeders do not influence the VP of the considered line.
Typically, the generators installed in Smart Grids are based on renewable energy; therefore, their power-time profiles are unknown. Due to the high generated power and a possibly low load condition, the voltage in some nodes can thus exceed the maximum admissible value ( ; i.e., the voltage threshold [8]) defined by the standards.
; i.e., the voltage threshold [8]) defined by the standards.
Of course the voltage threshold is strictly related with the settings of the voltage relays installed in the network, e.g. at the generator nodes [9].

Figure 1. Voltage profiles in a MV feeder with and without Distributed Generators
If the generators are able to control the injected or absorbed reactive power, the network voltage profiles can be modified by acting on the reactive powers. It is clear that each controllable generator needs a Generator Remote Terminal Unit (GRTU) that is connected to a central control system to set the generator reactive power, (i.e., to control the exciter of the synchronous generators [1] or act on the inverter control if the generator is inverter-based) [10,11]. In this work, the central control is called the Generator Control Centre (GCC). In addition, we use a hierarchical control structure [12,13].
Let us suppose that the voltage is measured only in the generator nodes by the GRTUs. This assumption does not affect the generality of the proposed method because a Measuring Remote Terminal Unit connected to the GCC can be installed in each node that must be controlled.
When the voltage in the ith node exceeds , the GRTU installed in the same node sends the signal “Voltage Threshold Overall” (VTO) to the GCC using a communication channel. The GCC then selects the generator in the jth node that has the maximum influence on the voltage of the ith node, the “Best Generator” (BG), and switches it to the reactive power absorption (RPA) mode. Therefore, the voltage in the ith node tends to decrease.
, the GRTU installed in the same node sends the signal “Voltage Threshold Overall” (VTO) to the GCC using a communication channel. The GCC then selects the generator in the jth node that has the maximum influence on the voltage of the ith node, the “Best Generator” (BG), and switches it to the reactive power absorption (RPA) mode. Therefore, the voltage in the ith node tends to decrease.
The problem is thus to determine the best generator and ensure that the GCC chooses it. In this work, a sensitivity-based method is proposed to select the BG.
Moreover, we suppose that the generators can only be switched in the RPA mode by the GCC by a constant power factor. Therefore, if  is the active power injectted by the generator connected to the jth node, then it absorbs the reactive power
is the active power injectted by the generator connected to the jth node, then it absorbs the reactive power  (where
(where  is the minimum power factor of the generator) when it is switched during RPA. In other words, we assume that no continuous reactive power modulation is possible.
is the minimum power factor of the generator) when it is switched during RPA. In other words, we assume that no continuous reactive power modulation is possible.
An example of the procedure described above is shown in Figure 2. Let us suppose that load Ld suddenly decreases its power (for example, due to a trip) and  exceed
exceed .
.
The GRTUs of G2 send the signal VTO to the GCC that must choose the BG using the sensitivity method. Assuming that the BG is G1, it will be switched by the

Figure 2. Voltage control using GRTU and GCC
GCC in the RPA mode; therefore, the reactive power absorbed by G1 becomes .
.
As explained in the following, the GCC must know the reactive power that each controllable generator can absorb in order to choose the BG. We suppose that this information is acquired by the GCC using a polling technique on each GRTU.
3. The Proposed Sensitivity Approach
3.1 Classical Sensitivity Theory Overview
The classical sensitivity theory used in HV network analysis to perform primary and secondary voltage regulation [14] is based on the Jacobian Matrix and reveals the relationships between the nodal voltages (magnitude and phase) and the nodal power injections (active and reactive). The relationships mentioned above are represented by the following matrix expression [2]:
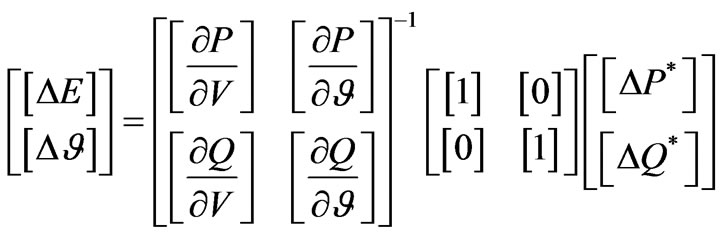
 (1)
(1)
where  and
and  are, respectively, the nodal voltage magnitudes (rms) and phase variations corresponding to the nodal active or reactive power injections
are, respectively, the nodal voltage magnitudes (rms) and phase variations corresponding to the nodal active or reactive power injections  and
and  (
( is the identity matrix).
is the identity matrix).
Equation (1) can be rewritten in the following compact form:
 (2)
(2)
where:
 (3)
(3)
is the (injection) sensitivity matrix. The method descries above is generally valid, but its computational complexity is too high for practical voltage analysis in MVDNs. For radial networks, only the voltage magnitude is needed to control the nodal voltages. The proposed theory is easier than classical theory, and it is suitable for radial MVDNs.
3.2 The Proposed Theory
In this section, the proposed theory for choosing the BG is outlined. The method is first described in general and considers the possibility of reactive power regulation for all nodes.
After the general treatment, the analysis focuses on a realistic network in which the reactive power can only be controlled in some nodes (generator nodes).
Let us consider the network depicted in Figure 3, which is a four-node test MVDN.
The general loads Ld1…Ld4 are represented using constant PQ models. Positive P (or Q) corresponds to the absorbed power by the load. Negative P (or Q) corresponds to the injected power in the network (i.e., the general load is really a generator). The per-phase equivalent circuit is shown in Figure 4.
The lines L01…L24 are modeled using the RL-direct sequence equivalent circuit [15], but the shunt admittances are neglected. The node 0 represents the MV busbar, which is regulated at a constant voltage value  by the AVR of the OLTC. This reference voltage coincides with the rated value
by the AVR of the OLTC. This reference voltage coincides with the rated value .
.
Because the busbar is regulated at , we can characterize the generic node i using the difference
, we can characterize the generic node i using the difference  between the magnitude of the busbar voltage and the node voltage
between the magnitude of the busbar voltage and the node voltage . In other words, we can write:
. In other words, we can write:
 (4)
(4)
In radial networks, (4) can be calculated as the sum of the voltage differences between adjacent nodes from the ith node toward the MV busbar. For example, if  (see Figure 4), (4) becomes:
(see Figure 4), (4) becomes:
 (5)
(5)

Figure 3. The considered four nodes test MVDN

Figure 4. The per-phase equivalent circuit
By adding and subtracting  and
and  in (5), we obtain:
in (5), we obtain:
 (6)
(6)
where  is the sum of the voltage differences
is the sum of the voltage differences ,
,  and
and .
.
 can be calculated considering the network parameters and the line power flows as follows:
can be calculated considering the network parameters and the line power flows as follows:
 (7)
(7)
where ,
,  and
and  are the power factor and the active and reactive (per-phase) powers of the load Ld3, respectively.
are the power factor and the active and reactive (per-phase) powers of the load Ld3, respectively. ,
,  and
and  are the current, resistance and reactance of the line L3.
are the current, resistance and reactance of the line L3.
Normally, the nodal voltages are close to the rated voltage . Applying this assumption to (7) leads to:
. Applying this assumption to (7) leads to:
 (8)
(8)
Similarly, considering nodes 1 and 2, we can write:
 (9)
(9)
where  and
and  are the active and reactive powers through the section S2 and
are the active and reactive powers through the section S2 and  is the power factor for the same section. For
is the power factor for the same section. For  and
and , we can write:
, we can write:
 (10)
(10)
 (11)
(11)
where  and
and  are the power losses in
are the power losses in  and
and , while
, while  and
and  are the reactive powers absorbed by
are the reactive powers absorbed by  and
and . These active and reactive losses are negligible compared to the load powers. Applying this assumption to (9), (10) and (11) leads to:
. These active and reactive losses are negligible compared to the load powers. Applying this assumption to (9), (10) and (11) leads to:
 (12)
(12)
 (13)
(13)
and:
 (14)
(14)
Finally, the voltage difference  is:
is:
 (15)
(15)
where:
 (16)
(16)
 (17)
(17)
are the powers through section .
.
Using (6) with (15), (9) and (8), we can say that  is a function of all loads and active and reactive powers, i.e., P1…P4 and Q1…Q4. The same observation is valid for
is a function of all loads and active and reactive powers, i.e., P1…P4 and Q1…Q4. The same observation is valid for :
:
 (18)
(18)
because  is constant. In other words, we can write:
is constant. In other words, we can write:
 (19)
(19)
Equation (19) shows that an active/reactive power variation (in the general  node) that is defined as:
node) that is defined as:
 (20)
(20)
 (21)
(21)
where  (
( ) and
) and  (
( ) are the final and initial power values, respectively, produces a voltage variation in node 3 that is defined as:
) are the final and initial power values, respectively, produces a voltage variation in node 3 that is defined as:
 (22)
(22)
In this treatment, we only consider the reactive power variations (i.e., ) because we assume that only the reactive power can be used to control the node voltages.
) because we assume that only the reactive power can be used to control the node voltages.
The variation  can be calculated by linearizing (19) and considering only the reactive power variations. In particular, we can write:
can be calculated by linearizing (19) and considering only the reactive power variations. In particular, we can write:
 (23)
(23)
The terms  in (23) indicate the “gain” from the voltage variation
in (23) indicate the “gain” from the voltage variation  in node
in node  when a reactive power variation
when a reactive power variation  occurs in node
occurs in node . In other words, they are sensitivity terms.
. In other words, they are sensitivity terms.
According to (18), we can obtain:
 (24)
(24)
Substituting equation group (24) into (23) has important implications. If we have a reactive injection in any node, i.e.,  (in this case
(in this case ), then
), then  in node 3 (i.e., the voltage increases). Then, if we were to reduce the voltage in any node, we must absorb reactive power from the network (i.e.,
in node 3 (i.e., the voltage increases). Then, if we were to reduce the voltage in any node, we must absorb reactive power from the network (i.e., ) by using, for example, the distributed generators.
) by using, for example, the distributed generators.
If the above analysis that focuses on node 3 is extended to all network nodes, (23) has a general matrix relationship:
 (25)
(25)
which in a compact form yields:
 (26)
(26)
where  is the reactive sensitivity matrix,
is the reactive sensitivity matrix,  is the reactive power-variations vector and
is the reactive power-variations vector and  is the nodal voltages vector.
is the nodal voltages vector.
Calculating the partial derivatives contained in , we have Equation (27).
, we have Equation (27).
 (27)
(27)
After analyzing this form of (27), we can say that this matrix can be built using the following inspection rule:
“The element  is the arithmetic sum of the reactance of the branches in which both the powers absorbed by node
is the arithmetic sum of the reactance of the branches in which both the powers absorbed by node  and node
and node  flow multiplied by
flow multiplied by ”.
”.
For example, in (27), the element 2, 4 is
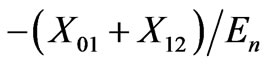
because the powers delivered by node 2 and node 4 flow in branches 01 and 12.
3.3 The Choice of the Best Generator
The BG is the generator that has the greatest influence on node , which is the node where the voltage exceeds the threshold.
, which is the node where the voltage exceeds the threshold.
Thus, after analyzing (25), we can say that the BG is the generator that maximizes the following product, which we call the “sensitivity product”:
 (28)
(28)
For example, if the node with a voltage that exceeds  is
is  and the BG is connected to node
and the BG is connected to node , the sensitivity product
, the sensitivity product  is the highest compared to the other products contained in row 2 of the sensitivity matrix. In addition, in order to choose the BG, it is necessary to evaluate the single products (28) of the row that represents node
is the highest compared to the other products contained in row 2 of the sensitivity matrix. In addition, in order to choose the BG, it is necessary to evaluate the single products (28) of the row that represents node . Thus, the value
. Thus, the value  is needed and is acquired as the GCC polls the GRTUs, as stated previously.
is needed and is acquired as the GCC polls the GRTUs, as stated previously.
The procedure described above suggests a way of defining the “sensitivity table”  that contains the single sensitivity products. For the MVDN represented in Figure 4,
that contains the single sensitivity products. For the MVDN represented in Figure 4,  takes the following form
takes the following form
 (29)
(29)
Row  represents the node in which we want to control the voltage, and column
represents the node in which we want to control the voltage, and column  represents the nodes in which we can control the reactive power. The BG is the generator connected to node
represents the nodes in which we can control the reactive power. The BG is the generator connected to node  that has the maximum absolute value of the sensitivity product in position
that has the maximum absolute value of the sensitivity product in position . By finding the maximum sensitivity product in row
. By finding the maximum sensitivity product in row ,
,
we automatically choose the BG because the location corresponds to column  of the maximum sensitivity product.
of the maximum sensitivity product.
It is clear that, for a general network with N nodes, the sensitivity table takes the following form:
 (30)
(30)
It is important to note that, if it is not possible to regulate the reactive power (e.g., if in that node there is a load or a non-controllable generator) in a node , then
, then  and, consequently, the sensitivity product in the position
and, consequently, the sensitivity product in the position  of the sensitivity table is 0.
of the sensitivity table is 0.
Comparing (29) with (25), we can say that each element  of
of  represents the line-to-ground voltage variation in node
represents the line-to-ground voltage variation in node  when a reactive power variation occurs in node
when a reactive power variation occurs in node .
.
In the following section, a numerical example of the sensitivity method application is shown.
4. Application of the Proposed Method
The network considered in this numerical application is represented in Figure 5.
During normal network operation, we have four generators and eight loads. The generator and load characteristics are summarized in Table 1 (S is the apparent power) and Table 2, respectively (three-phase powers are represented in these tables).
We suppose that the generators normally operate with a unitary power factor (i.e., no reactive power is injected in the nodes).
The per-kilometer reactance of the cable lines is 
 , which is a typical value for Italian MVDNs. The line lengths and parameters are summarized in Table 3.
, which is a typical value for Italian MVDNs. The line lengths and parameters are summarized in Table 3.
Let us suppose that each generator is connected to its GRTU that measures the nodal voltage and communicates with the GCC. Moreover, let us suppose that G5 cannot regulate the reactive power because it is not designed for this purpose. The MV busbar is regulated at the rated voltage (1 p.u.), which is 20 kV (line-to-line). In this example, the voltage threshold  is 1.05 p.u.
is 1.05 p.u.
Using load-flow software, we calculated the voltage E in the generator nodes (nodes 4, 5, 6, and 7) for normal network operation. The results are shown in Figure 6 (Normal Operation).

Figure 5. The network considered in the numerical application

Table 2. Generators characteristics
If line b trips (e.g., due to a fault), loads bl, cl and dl are cut off from the supply, which causes the voltage to increase in the network. In particular, if the load-flow is re-computed to take into account the new network configuration, we obtain the results shown in Figure 6 (Tripped Line).
It is important to note that, if the voltage exceeds the maximum threshold  in node 5, the GRTU connected to G5 sends the VTO signal to the GCC that must choose the BG using the sensitivity table.
in node 5, the GRTU connected to G5 sends the VTO signal to the GCC that must choose the BG using the sensitivity table.
We suppose that the three-phase reactive powers absorbable by each generator that were collected from the last poll are those summarized in Table 4, which also contains the corresponding power factors cosφ. To calculate the sensitivity table, we need the single-phase powers. Therefore, the reactive powers shown in Table 4 have to be divided by three. It is important to note that the reactive powers calculated this way correspond to  because
because  is zero (see (21)). The
is zero (see (21)). The  values are shown in Table 5.
values are shown in Table 5.
The voltage exceeds the threshold in node 5. Thus, we only consider the fifth row of the sensitivity table. According to the inspection rule mentioned above, this row is as follows:
 (31)
(31)
where the single sensitivity products  are:
are:
 (32)
(32)
 (33)
(33)

Figure 6. Load-Flow results with the Network Normal Operation

Table 4. Reactive powers absorbable by the generators

Table 5. Reactive Power Variations in the Generator Nodes
 (34)
(34)
 (35)
(35)
The maximum sensitivity product (in absolute value) corresponds to generator 4, (i.e., ). Thus, the BG is G4.
). Thus, the BG is G4.
Equation (32) provides important information. If G4 performs the considered reactive power variation, the line-to-ground voltage variation in node 5 is:
 (36)
(36)
Then, considering (22) (rewritten for node 5), and  from Figure 6, we can say that the voltage value after the reactive power variation is:
from Figure 6, we can say that the voltage value after the reactive power variation is:
 (37)
(37)
which is less than the voltage threshold .
.
Equation (37) shows the theoretical result obtained using the proposed method. We checked this value using load-flow software:
 (38)
(38)
The percentage error between (38) and (37) is:
 (39)
(39)
which is negligible and demonstrates the validity of the proposed approach.
5. Conclusions
The proposed sensitivity method allows the voltage within network acting on single generators to be regulated by choosing the most effective generator on the controlled node (i.e., the Best Generator). This is a very important feature in grids that have distributed generation (e.g., in a Smart Grid context).
The proposed method uses a topological approach. Moreover, the sensitivity table can be constructed automatically.
In addition to the BG choice, the proposed method also evaluates the voltage in all network nodes after a reactive power variation.
After choosing the BG, but before its commutation during RPA, it is possible to verify that the voltage variation in the other nodes is tolerable for the connected loads. Moreover, it is necessary to verify that the threshold settings of the voltage relay installed in the same nodes.
When a generator is switched during RPA, it works with a non-unitary power factor; the reactive power flow increases along the lines and increases the power loss [16].
This phenomenon is negligible in HV networks because the line resistance is typically smaller than the line reactance, but is important to consider in MV networks.
Therefore, if network analysis reveals that the RPAswitching produces high losses, voltage control using the reactive power variation must only be used for temporary voltage variation mitigation (i.e., during emergency conditions).
The possible future develops of this work could be focused on the optimization of the forecasted power-time profiles of the loads and generators applying both the se nsitivity approach and distributed voltage measurement.