1. Introduction
Suppose 
are 
independent and identically distributed observations from a distribution
, where 
is differentiable with a density 
which is positive in an interval and zero elsewhere. The order statistics of the sample is defined by the arrangement of 
from the smallest to largest denoted as
. Then the p.d.f. of the 
order statistics
, is given by
(1)
for details refer to [1].
Order statistics has been studied by statisticians for some time and has been applied to problems of statistical estimation [2], reliability analysis, image coding [3] etc. Some information theoretic aspects of order statistics have been discussed in the literature. Wong and Chen [4] showed that the difference between average entropy of order statistics and the entropy of a data distribution is a constant. Park [5] showed some recurrence relations for entropy of order statistics. Information properties of order statistics based on Shannon entropy [6] and Kullback-Leibler [7] measure using probability integral transformation have been studied by Ebrahimi et al. [8]. Arghami and Abbasnejad [9] studied Renyi entropy properties based on order statistics. The Renyi [10] entropy is a single parameter entropy. We consider a generalized two parameter, the Verma entropy [11], and study it in context with order statistics. Verma entropy plays a vital role as a measure of complexity and uncertainty in different areas such as physics, electronics and engineering to describe many chaotic systems. Considering the importance of this entropy measure, it will be worthwhile to study it in case of order statistics. The rest of the article is organized as follows:
In Section 2, we express generalized entropy of 
order statistics in terms of generalized entropy of 
order statistics of uniform distribution and study some of its properties. Section 3 provides bounds for entropy of order statistics. In Section 4, we derive an expression for residual generalized entropy of order statistics using residual generalized entropy for uniform distribution.
2. Generalized Entropy of Order Statistics
Let 
be a random variable having an absolutely continuous cdf 
and pdf
, then Verma [11] entropy of the random variable 
with parameters 
is defined as:
(2)
where
is the Renyi entropy, and
is the Shannon entropy .
We use the probability integral transformation of the random variable 
where the distribution of U is the standard uniform distribution. If 
are the order statistics of a random sample 
from uniform distribution, then it is easy to see using (1) that 
has beta distribution with parameters 
and
. Using probability integral transformation, entropy (2) of the random variable 
can be represented as
(3)
Next, we prove the following result:
Theorem 2.1 The generalized entropy of 
can be expressed as
(4)
where 
denotes the entropy of the beta distribution with parameters 
and
, 
denotes expectation of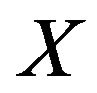 
over 
and 
is the beta density with parameters 
and
.
Proof: Since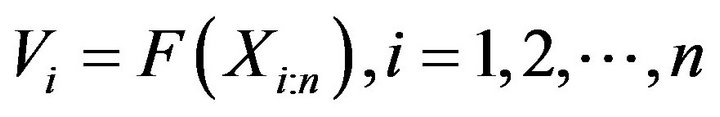 
which implies
. Thus, from (3) we have
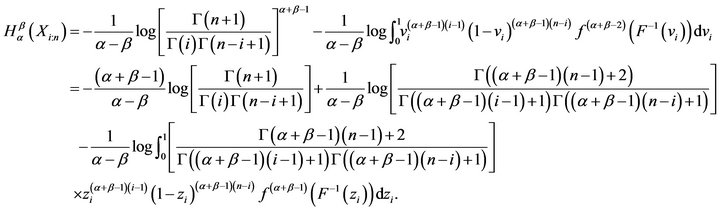(5)
It is easy to see that the entropy (2) for the beta distribution with parameters 
and 
(that is, the 
order statistics of uniform distribution) is given by
(6)
Using (6) in (5), the desired result (4) follows.
In particular, by taking
, (4) reduces to
a result derived by Ebrahimi et al. [8].
Remark: In reliability engineering 
-outof-
systems are very important kind of structures. A 
-out-of-
system functions iff atleast
components out of 
components function. If 
denote the independent lifetimes of the components of such system, then the lifetime of the system is equal to the order statistic
. The special case of 
and
, that is for sample minima and maxima correspond to series and parallel systems respectively. In the following example, we calculate entropy (4) for sample maxima and minima for an exponential distribution.
Example 2.1 Let 
be a random variable having the exponential distribution with pdf
Here, 
and the expectation term is given by
For
, from (6), we have
Hence, using (4)
which confirms that the sample minimum has an exponential distribution with parameter
, since
where 
is an exponential variate with parameter
. Also
Hence, the difference between the generalized entropy of first order statistics i.e. the sample minimum and the generalized entropy of parent distribution is independent of parameter
, but it depends upon sample size
. Similarly, for sample maximum, we have
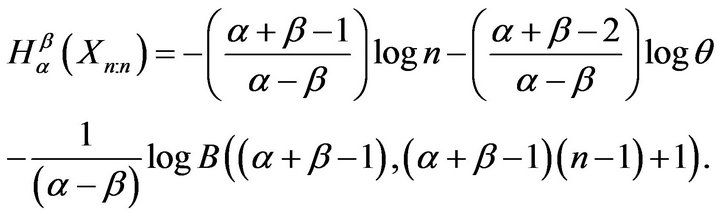
It can be seen easily that the difference between 
and 
is
which is also independent of parameter
.
3. Bounds for the Generalized Entropy of Order Statistics
In this section, we find the bounds for generalized entropy for order statistics (4) in terms of entropy (2). We prove the following result.
Theorem 3.1 For any random variable 
with
, the entropy of the 
order statistics 
is bounded above as
(7)
where
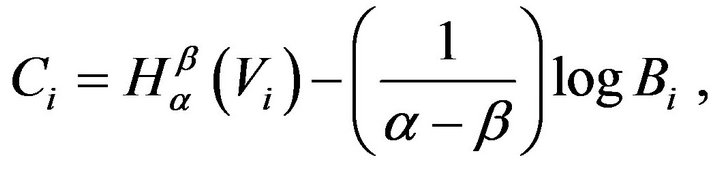
and, bounded below as
(8)
where, 
, and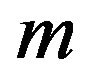 
is the mode of the distribution and 
is pdf of the random variable
.
Proof: The mode of the beta distribution 
is
. Thus,
For
, from (4)
which gives (7).
From (4) we can write
Example 3.1 For the uniform distribution over the interval 
we have
and from (6),
and
Hence, using (7) we get
Further, for uniform distribution over the interval
,
. Using (8) we get
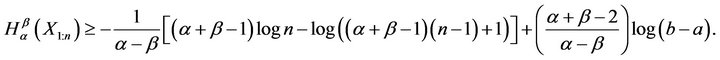
Thus, for uniform distribution, we have
We can check that the bounds for 
are same as that of
.
Example 3.2 For the exponential distribution with parameter
, we have 
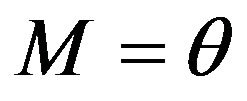and
Thus, as calculated in Example 2.1
Using Theorem 3.1
Here we observe that the difference between upper bound and 
is
, which is an increasing function of n. Thus, for the exponential distribution upper bound is not useful when sample size is large.
4. The Generalized Residual Entropy of Order Statistics
In reliability theory and survival analysis, 
usually denotes a duration such as the lifetime. The residual lifetime of the system when it is still operating at time
, given by 
has the probability density
, where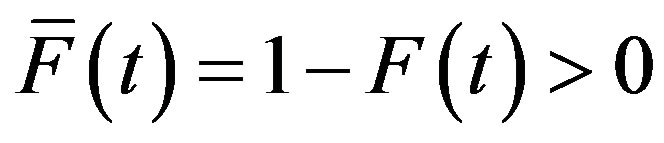
. Ebrahimi [12] proposed the entropy of the residual lifetime 
as
(9)
Obviously, when
, it reduces to Shannon entropy.
The generalized residual entropy of the type 
is defined as
(10)
where
. When
, it reduces to (2).
We note that the density function and survival function of 
(refer to [13]), denoted by 
and
, respectively are
(11)
where
(12)
and
(13)
where
(14)
and 
are known as the beta and incomplete beta functions respectively. In the next lemmawe derive an expression for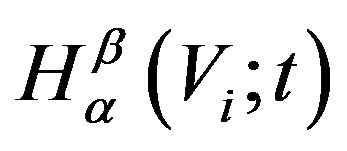 
for the dynamic version of 
as given by (6).
Lemma 4.1 Let 
be the 
order statistics based on a random sample of size 
from uniform distribution on
. Then
(15)
Proof: For uniform distribution using (10), we have
(16)
Putting values from (11) and (13) in (16), we get the desired result (15).
If we put 
in (15), we get (6).
Using this, in the following theorem, we will show that the residual entropy of order statistics 
can be represented in terms of residual entropy of uniform distribution.
Theorem 4.1 Let 
be an absolutely continuous distribution function with density
. Then, generalized residual entropy of the 
order statistics can be represented as
(17)
where
Proof: Using the probability integral transformation
and above lemma, the result follows.
Take 
in (17), it reduces to (4).
Example 4.1 Suppose that 
is exponentially distributed random variable with mean
. Then,
and we have
For
, Theorem 4.1 gives
Also
Hence
So, in the exponential case the difference between generalized residual entropy of the lifetime of a series system and residual generalized entropy of the lifetime of each component is independent of time.
5. Conclusion
The two parameters generalized entropy plays a vital role as a measure of complexity and uncertainty in different areas such as physics, electronics and engineering to describe many chaotic systems. Using probability integral transformation we have studied the generalized and generalized residual entropies based on order statistics. We have explored some properties of these entropies for exponential distribution.
6. Acknowledgements
The first author is thankful to the Center for Scientific and Industrial Research, India, to provide financial assistance for this work.