Analytical expressions of steady-state concentrations of species in potentiometric and amperometric biosensor ()
1. INTRODUCTION
Theoretical models of enzyme electrodes give information about the mechanism and kinetics of the biosensor. The information gained from mathematical modeling can be useful in sensor design, optimization and predict tion of the electrode’s response. Enzyme-based systems, i.e. the combination of enzyme-reactor sensor and enzyme electrodes have gained considerably more importance for chemical analysis and also for clinical diagnostics [1,2]. Blaedel et al. [3] have derived explicit solution of electrodes for steady-state conditions which can apply to very high substrate concentration or to sufficiently low substrate concentration. Guilbault and Nagy [4] proposed an approximation which is used for sensors with very thin enzyme membranes in contact with diluted substrate samples. Hameka and Rechnitz [5] have used Laplace transforms to treat potentiometric enzyme electrodes. Tranh-Minh and Broun [6] also solved the differential equations for reaction and diffusion processes by using a numerical method. Morf [7,8] presented a relatively simple approach for the electrode response that applies to the whole range of substrate concentrations by obtaining an explicit result. Glab et al. [9-11] extended this theory to account for additional influence arising from the presence of pH-buffering systems. Mell and Maloy [12,13] have obtained the current response as a function of time and substrate concentration using numerical simulation. Olesson et al. [14] treated the behavior of these sensors in flow-injection analysis applications. Albery and Bartlett [15] studied the steady-state current response of modified enzyme-based sensors where electron transfer from the enzyme to the electrode occurs directly by a redox mediator. Later these authors [16] have derived 11 equations to differentiate between 7 limiting cases by offering a complete theoretical treatment of the basic reaction and diffusion processes in homogeneous solution. Mackey et al. [17] recently studied the current efficiency of sensors with a monolayer of two enzymes.
Several groups [18-20] introduced numerical method for the study of amperometric and cyclic-voltammetric enzyme electrodes based on Michaelis-Menten kinetics. The available theoretical descriptions of enzyme electrodes seem to be quite complex. Reaction and diffusion processes in the enzyme layer are modeled by a finitedifference method [21-32]. Morf et al. [33] presented the theoretical model for an amperometric glucose sensor for low substrate concentration and high benzoquinone concentration compared with respective Michaelis constants. To my knowledge no rigorous analytical expression of concentration of substrate and mediator of ampereometric glucose sensor under steady-state conditions for all values of parameters have been reported. The purpose of this communication is to derive approximate analytical expressions for the steady-state concentrations and flux for all values of parameters α, β and γ using Homotopy analysis method. This dimensionless parameter are defined in the Eq.6.
2. MATHEMATICAL FORMULATION OF THE PROBLEM
In this paper we consider the analytical systems based on an enzyme-containing bulk membrane of thickness d that is contacted on one side with an aqueous solution of the substrate S (refer Figure 1).
The substrate molecules entering the membrane phase react according to a Michaelis-Menten type enzymecatalyzed reaction [31,32] to yield an electroactive product P. The corresponding governing equations in Cartesian coordinates for planar diffusion and reaction in a membrane may be written as follows [33,34]:
(1)
(2)
where 
and 
are the concentrations of the species in the enzyme membrane, DS and DP are the corresponding diffusion coefficients, 
is the total concentration of free enzymes and enzyme-substrate complexes that is assumed to be constant within the membrane including the surface zones, v is the number of product species obtained per substrate molecule, k3 is the rate constant for the irreversible step of product formation, and KM the Michaelis constant [31,32]. The Eqs.1 and 2 are solved for the following boundary conditions by assuming the zero fluxes at x = 0 and of equilibrium distribution at x = d [33,34].
(3)
(4)
For enzyme reactors, the outward flux of product species at x = d is described by:
(5)
where JP is the outward flux of the product species and DP is the diffusion coefficient of the product.
3. DIMENSIONLESS FORM OF THE PROBLEM
To compare the analytical results with simulation results, we make the above non-linear partial differential equations Eqs.1 and 2 in dimensionless form by defining
(a) Potentiomtric enzyme electrode 
(b) Amperometric enzyme electrode
Figure 1. Various analytical scheme of enzyme-based system.
the following parameters:
(6)
The Eqs.1 and 2 reduces to the following dimensionless form:
(7)
(8)
where u and v represents the dimensionless concentration of substrate and product. α and β are saturation parameter and γ is the reaction/diffusion parameter (Thiele modulus). Now the boundary conditions may be presented as follows [33,34]:
(9)
(10)
4. ANALYTICAL SOLUTIONS USING HOMOTOPY ANALYSIS METHOD
Recently, Homotopy analysis method (HAM) has been developed to solve different types of non-linear problems. Many problems of engineering and allied disciplines have been successfully solved [35,36]. The major advantages of this method are that it does not require the presence of small/large parameter unlike the perturbation method or delta decomposition method and can be applied to any type of nonlinearity. Further, working of HAM reduces to those of other methods for a certain choice of auxiliary quantities defined later [36,37], and it can easily be implemented in various symbolic soft computing tools e.g. MATHEMATICA, MAPLE etc. A details of this method can be found in the original work of Liao [36]. The Homotopy analysis method [38,39] was first proposed by Liao in 1992. The basic concept of Homotopy analysis method is given in [40]. By solving the above Eq.7 using HAM [38-44], we can obtain the concentration of substrate in dimensionless form as follows:
(11)
Detailed derivation of the above Eq.11 is described in Appendix A. Adding the Eqs.7 and 8 we get
(12)
Integrate the above Eq.12 twice and using the boundary conditions (9) and (10), we can obtain the concentration of product as follows:
(13)
The normalized flux becomes,
(14)
The above equation represent the dimensional flux for all values of parameter for steady state conditions.
5. LIMITING CASES
5.1. Limiting Case: 1-Unsaturated (First-Order) Catalytic Kinetics
We consider the situation when the substrate concentration is sufficiently low, that is for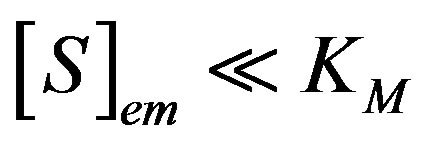
, the catalytic reaction follows first-order kinetics. This situation will pertain when the product
. Hence Eqs.7 and 8 are reduces to
(15)
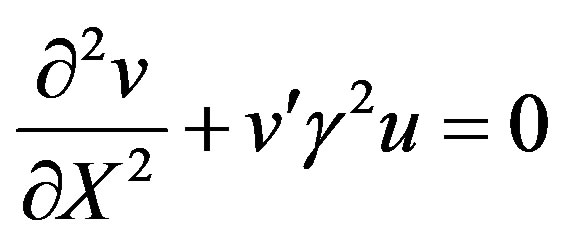(16)
Hence the non-linear reaction/diffusion equation Eqs.7 and 8 has been reduced to the linear equation. Hence the concentration profiles of substrate and product are given by:
(17)
(18)
In this case the dimensionless flux becomes
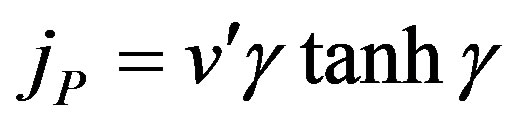(19)
The Eqs.17 and 18 are same as Eqs.7 and 8 in [33].
5.2. Limiting Case: 2-Saturated (Zero-Order) Catalytic Kinetics
For very high substrate concentrations, 
, the enzyme-catalyzed reaction becomes zero-order kinetics. In this case 
and Eqs.7 and 8 reduces to
(20)
(21)
Now the concentration of substrate and product becomes as follows:
(22)
(23)
The normalized flux is given by
(24)
Recently Morf et al. [33] have derived the above (Eqs.22-24) same results (Eqs.14 and 15) in Ref. [33].
6. NUMERICAL SIMULATION
The two non-linear reaction/diffusion equations (Eqs.7 and 8) corresponding to the boundary conditions (Eqs.9 and 10) were solved by numerical methods. We have used pdex4 to solve these equations (Pdex4 in MATLAB is a function to solve the initial-boundary value problems of differential equations). The numerical solution is compared with our analytical results and is shown in Figures 2 and 3. Tables 1-4 illustrate the comparison of analytical result obtained in this work with the numerical result. The relative difference between numerical and analytical results are within 0.68% for all possible values of parameters considered in this work. A satisfactory agreement is noticed for various values of the Thiele modulus and possible small values of reaction/diffusion parameters.
7. DISCUSSION
7.1. Concentrations
The reaction diffussion parameter γ, is indicative of the competition between the reaction and diffusion in the matrix. When γ is small the kinetics dominate and the uptake of substrate is kinetically controlled. The overall kinetics are governed by the total amount of active enzyme, i.e.
. When γ is large, diffusion limitations
(a)
(b)
Figure 2. Dimensionless steady-state concentration profiles of the substrate u for various values of γ using the Eq.11. (a) The h value is –1; (b) a) b), e), f); h = –0. 5, c); h = –0. 7, d); h = –1. Solid lines represent the numerical simulation and the dotted lines represent the analytical solution.
are the principal determining factor. The concentration gradient near the electrode, and hence the flux of substrate to the electrode, decreases with an increase in γ. For a given layer, and hence value of γ, the concentration profile is also altered according to the bulk concentration of the substrate. Thus an increased substrate concentration causes a decrease in the flux to the electrode. Eqs.11 and 13 are the new and simple analytical expressions of concentrations of substrate and product respectively. The analytical expression of concentration of substrate, product and flux are summarized in Tables 5 and 6.
In Figures 2 and 3, the profiles of substrate as well as product concentration in the enzyme layer are presented. The normalized concentration of substrate is represented in Figures 2(a) and (b). From this Figure, it is evident that the value of substrate concentration S decreases
Table 1. Comparison of normalized steady-state concentration of substrate u with the numerical results for various values of γ and for some fixed values of saturation parameter α (= 0.1) and h = –1.
Table 2. Comparison of normalized steady-state concentration of substrate u vwith the numerical results for various values of γ and for some fixed values of saturation parameter α (= 1) and h = –0.5 to –0.7.
Table 3. Comparison of normalized steady-state concentration of product v th the numerical results for various values of γ and for some fixed values of saturation parameter α = 0.01, β = 0.005 and v' = 0.5. Here h = –1.
Table 4. Comparison of normalized steady-state concentration of product v with the numerical results for various values of γ and for some fixed value of saturation parameter α = 0.1, β = 0.05 and v' = 0.5. Here h = –1.
when the reaction diffusion parameter γ increases for all values of α. When γ is very small , the concentration of substrate is uniform and the curve becomes straight line. In Figures 3(a)-(c) represent the normalized concentration of product P for various values of γ.
From this Figure it is obvious that the value of the product concentration P increases when the reaction diffusion parameter γ increases for various values of α. Figures 4(a) and (b) represent the normalized concentration of the substrate S and the product P for various values of γ. From this Figure it is clearly that the value of substrate concentration S decreases and the value of the product concentration P increases. From the Figures 2-4, it is also confirmed that when the thickness of the mem
Table 5. Analytical expression of concentration of substrate, product and flux for limiting cases.
Table 6. Analytical expression of concentration of substrate, product and flux.
(a) α = 0.01 
(b)α = 1
Figure 4.Dimensionless steady-state concentration profiles of the substrate u and product v for various values of γ using the Eqs.11, 13. Here in the above cases
, v' = 0.5 and the h value of (a) and (b) is –1.
(a)
(b)
Figure 5. The h-curve of u(1) and to u'(1) given by Eq.11. (a) 2nd-order approximation of u(1); (b) 2nd-order approximation of u'(1).
Figure 6. Profiles of the dimensionless flux versus γ using the Eq.14. For α = 0.01 to 10 the value of h = –1.
Figure 7. Profiles of the dimensionless flux versus α using the Eq.14. For γ = 0.01 to 50 the value of h = –1.
brane decrease, the concentration of substrate increase and the product decrease.
7.2. Convergence Parameter h
The auxiliary convergent parameter h controls the convergence of the analytical solution series [36]. The Eq.11 and Eq.13 contain the parameter h, which gives the convergence region for the Homotophy analysis method. Multiple h curves are plotted to define the h region such that the analytical solution series is independent of h. The common region among 
and its derivative 
is known as the convergence region for the corresponding function u. The h curves in Figures 5(a) and (b) represent the valid region of h is –1 when α = 0.1 and γ = 5. Similarly the value of the convergence parameter h can be obtained for different values of parameters α and γ.
7.3. Flux
The parameter of greatest interest in an amperometric biosensor is the current which is related to the flux of electroactive material to the electrode surface. For a particular membrane, the variation in γ can be achieved practically, by varying the thickness of the membrane, d, or the loading of the enzyme,
. As can be seen in Eq.14, and confirmed above, the thickness appears as a squared term and thus small changes will have a much more pronounced effect on the response of the enzyme electrode than the enzyme loading.
In Figure 6 characterize the dimensionless flux versus the dimensionless reaction/diffusion parameter γ for various values of α. From this Figure, it is obvious that, the value of flux decreases when γ increases. The flux versus the dimensionless parameter α for different values of γ is plotted in Figure 7. In this Figure, the value of flux increases when γ increases. And also the current is uniform for γ ≤ 5.
8. CONCLUSION
We have theoretically analyzed the behavior of potentiometric and amperometric enzyme electrodes, which is previously described in Ref. [33]. The coupled time independent steady-state non-linear reaction/diffusion equations have been solved analytically and numerically. In this work, we have presented analytical expression corresponding to the substrate and product concentration within the polymer film in terms of parameters using Homotopy analysis method. Moreover, we have also obtained an analytical expression for the steady state current. A good agreement with numerical simulation data is noticed. The analytical results presented here will be used to determine the kinetic characteristic of the biosensor. The theoretical model described here can be used for optimization of the design of the biosensor. Further, based on the outcome of this work it is possible to extend the procedure to find the approximate amounts of substrate and product concentrations and current for reciprocal competitive inhibition process.
9. ACKNOWLEDGEMENTS
This work as supported by the Council of Scientific and Industrial Research (CSIR No.: (2442)/10/EMR-II), Government of India. (F. No. 39-58/2010(SR)), New Delhi, India. The authors are thankful to the Secretary, the Principal, The Madura College, Madurai for their encouragement.
APPENDIX A: ANALYTICAL SOLUTION OF EQ.7 USING HOMOTOPY ANALYSIS METHOD
The zero-order deformation equation of non-linear Eq.7 is
(A1)
where 
is an embedding parameter and 
is the so-called convergence parameter. When p = 0, the Eq.A1 becomes
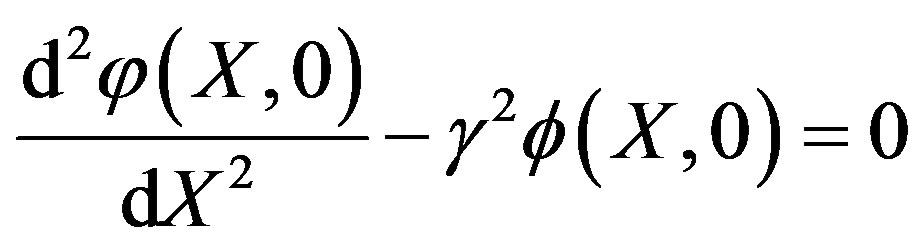(A2)
The boundary conditions are
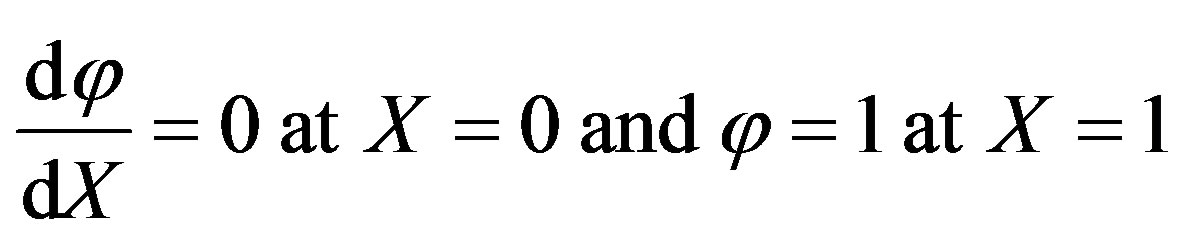. (A3)
The solution of Eq.A2 using boundary condition (A3) is
. (A4)
When 
the Eq.A1 is equivalent to Eq.7. Thus it holds
. (A5)
Expanding 
in Taylor series with respect to the embedding parameter p, we have,
(A6)
where
(A7)
(A8)
Note that the series Eq.A6 contains the convergence control parameter h. Assuming that h is chosen so properly that the above series is convergent at
. We have the solution series as
(A9)
Substituting Eq.A6 into the zeroth-order deformation Eq.A1 and equating the co-efficient of p we have,
(A10)
The boundary conditions are
(A11)
From Eq.A10 we get
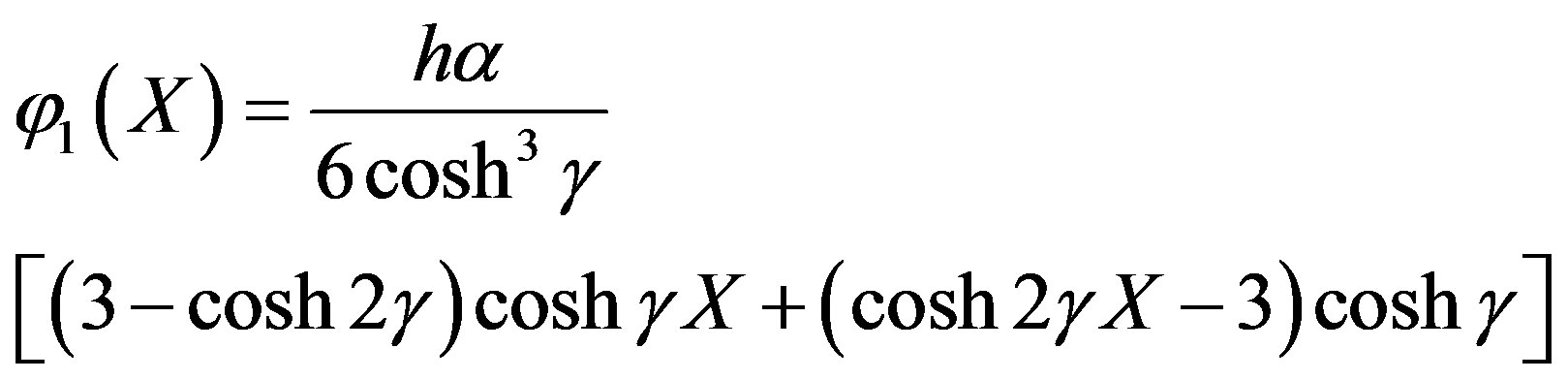(A12)
Adding Eqs.A4 and A12, we get Eq.11 in the text.
APPENDIX B: MATLAB/SCILAB PROGRAM TO FIND THE NUMERICAL SOLUTION OF THE EQS.7 AND 8
function pdex4 m = 0;
x = linspace(0,1); %d=1 t=linspace(0,10);
sol = pdepe(m,@pdex4pde,@pdex4ic,@pdex4bc,x,t);
u1 = sol(:,:,1);
u2 = sol(:,:,2);
figure plot(x,u1(end,:))
title('u1(x,t)')
xlabel('Distance x')
ylabel('u1(x,2)')
%-----------------------------------------------------------------
figure plot(x,u2(end,:))
title('u2(x,t)')
xlabel('Distance x')
ylabel('u2(x,2)')
% -------------------------------------------------------------
function [c,f,s] = pdex4pde(x,t,u,DuDx)
c = [1; 1];
f = [1; 1] .* DuDx;
gamma=100;
alpha=100;
v=0.1;
%beta=0.5;
F=-(gamma^2*u(1))/(alpha*u(1)+1);
F1=(v*(gamma^2*u(1)/(alpha*u(1)+1)));
s=[F; F1];
% -------------------------------------------------------------
Functionu0=pdex4ic(x); %create a initial conditions u0 = [1; 1];
% -------------------------------------------------------------
function[pl,ql,pr,qr]=pdex4bc(xl,ul,xr,ur,t)
%create a boundary conditions pl = [0; 0];
ql = [1; 1];
pr = [ur(1)-1; ur(2)];
qr = [0; 0];
APPENDIX C: NOMENCLATURE AND UNITS
