1. Introduction
By a rhotrix A of dimension three, we mean a rhomboidal array defined as

where, . The entry
. The entry  in rhotrix
in rhotrix  is called the heart of
is called the heart of  and it is often denoted by
and it is often denoted by . The concept of rhotrix was introduced by [1] as an extension of matrix-tertions and matrix noitrets suggested by [2]. Since the introduction of rhotrix in [1], many researchers have shown interest on development of concepts for Rhotrix theory that are analogous to concepts in Matrix theory (see [3-9]). Sani [7] proposed an alternative method of rhotrix multiplication, by extending the concept of row-column multiplication of two dimensional matrices to three dimensional rhotrices, recorded as follows:
. The concept of rhotrix was introduced by [1] as an extension of matrix-tertions and matrix noitrets suggested by [2]. Since the introduction of rhotrix in [1], many researchers have shown interest on development of concepts for Rhotrix theory that are analogous to concepts in Matrix theory (see [3-9]). Sani [7] proposed an alternative method of rhotrix multiplication, by extending the concept of row-column multiplication of two dimensional matrices to three dimensional rhotrices, recorded as follows:
 where,
where,  and
and  belong to set of all three dimensional rhotrices,
belong to set of all three dimensional rhotrices, .
.
The definition of rhotrix was later generalized by [6] to include any finite dimension  Thus; by a rhotrix A of dimension
Thus; by a rhotrix A of dimension  we mean a rhomboidal array of cardinality
we mean a rhomboidal array of cardinality . Implying a rhotrix R of dimension n can be written as
. Implying a rhotrix R of dimension n can be written as

The element and
and  are called the major and minor entries of R respectively. A generalization of row-column multiplication method for n-dimensional rhotrices was given by [8]. That is, given any n-dimensional rhotrices
are called the major and minor entries of R respectively. A generalization of row-column multiplication method for n-dimensional rhotrices was given by [8]. That is, given any n-dimensional rhotrices  and
and , the multiplication of
, the multiplication of  and
and  is as follows:
is as follows:

The method of converting a rhotrix to a special matrix called “coupled matrix” was suggested by [9]. This idea was used to solve systems of  and
and  matrix problems simultaneously. The concept of vectors and rhotrix vector spaces and their properties were introduced by [3] and [4] respectively. To the best of our knowledge, the concept of rank and linear transformation of rhotrix has not been studied. In this paper, we consider the rank of a rhotrix and characterize its properties. We also extend the idea to suggest the necessary and sufficient condition for representing rhotrix linear transformation.
matrix problems simultaneously. The concept of vectors and rhotrix vector spaces and their properties were introduced by [3] and [4] respectively. To the best of our knowledge, the concept of rank and linear transformation of rhotrix has not been studied. In this paper, we consider the rank of a rhotrix and characterize its properties. We also extend the idea to suggest the necessary and sufficient condition for representing rhotrix linear transformation.
2. Preliminaries
The following definitions will help in our discussion of a useful result in this section and other subsequent ones.
2.1. Definition
Let  be an n-dimensional rhotrix. Then,
be an n-dimensional rhotrix. Then,
 is the
is the  -entries called the major entries of
-entries called the major entries of 
and  is the
is the  -entries called the minor entries of
-entries called the minor entries of .
.
2.2. Definition 2.2 [7]
A rhotrix  of n-dimension is a coupled of two matrices
of n-dimension is a coupled of two matrices  and
and  consisting of its major and minor matrices respectively. Therefore,
consisting of its major and minor matrices respectively. Therefore,  and
and  are the major and minor matrices of
are the major and minor matrices of .
.
2.3. Definition
Let  be an n-dimensional rhotrix. Then, rows and columns of
be an n-dimensional rhotrix. Then, rows and columns of  (
( ) will be called the major (minor) rows and columns of
) will be called the major (minor) rows and columns of  respectively.
respectively.
2.4. Definition
For any odd integer n, an  matrix
matrix  is called a filled coupled matrix if
is called a filled coupled matrix if  for all
for all  whose sum
whose sum  is odd. We shall refer to these entries as the null entries of the filled coupled matrix.
is odd. We shall refer to these entries as the null entries of the filled coupled matrix.
2.5. Theorem
There is one-one correspondence between the set of all n-dimensional rhotrices over  and the set of all
and the set of all  filled coupled matrices over
filled coupled matrices over .
.
3. Rank of a Rhotrix
Let , the entries
, the entries  and
and
 in the main diagonal of the major and minor matrices of
in the main diagonal of the major and minor matrices of  respectively, formed the main diagonal of R. If all the entries to the left (right) of the main diagonal in
respectively, formed the main diagonal of R. If all the entries to the left (right) of the main diagonal in  are zeros,
are zeros,  is called a right (left) triangular rhotrix. The following lemma follows trivially.
is called a right (left) triangular rhotrix. The following lemma follows trivially.
3.1. Lemma
Let  is a left (right) triangular rhotrix if and only if
is a left (right) triangular rhotrix if and only if  and
and  are lower (upper) triangular matrices.
are lower (upper) triangular matrices.
wang#title3_4:spProof
This follows when the rhotrix  is being rotated through 45˚ in anticlockwise direction.
is being rotated through 45˚ in anticlockwise direction.
In the light of this lemma, any n-dimensional rhotrix  can be reduce to a right triangular rhotrix by reducing its major and minor matrix to echelon form using elementary row operations. Recall that, the rank of a matrix
can be reduce to a right triangular rhotrix by reducing its major and minor matrix to echelon form using elementary row operations. Recall that, the rank of a matrix  denoted by
denoted by  is the number of non-zero row(s) in its reduced row echelon form. If
is the number of non-zero row(s) in its reduced row echelon form. If , we define rank of
, we define rank of  denoted by
denoted by  as:
as:
 . (3)
. (3)
It follows from equation (3) that many properties of rank of matrix can be extended to the rank of rhotrix. In particular, we have the following:
3.2. Theorem
Let  and
and , be any two n-dimensional rhotrices, where
, be any two n-dimensional rhotrices, where  Then 1)
Then 1) ;
;
2) ;
;
3) ;
;
4) .
.
wang#title3_4:spProof
The first two statements follow directly from the definition. To prove the third statement, we apply the corresponding inequality for matrices, that is,  , where
, where  is
is  and
and  is
is . Thus,
. Thus,

For the last statement, consider

3.3. Example
Let
 .
.
Then, the filled coupled matrix of  is given by
is given by
 .
.
Now reducing  to reduce row echelon form
to reduce row echelon form  , we obtain
, we obtain
 which is a coupled of
which is a coupled of  and
and  matrices, i.e.
matrices, i.e.
 and
and  respectively.
respectively.
Notice that,

Hence,  .
.
4. Rhotrix Linear Transformation
One of the most important concepts in linear algebra is the concept of representation of linear mappings as matrices. If  and
and  are vector spaces of dimension
are vector spaces of dimension  and
and  respectively, then any linear mapping
respectively, then any linear mapping  from
from  to
to  can be represented by a matrix. The matrix representation of
can be represented by a matrix. The matrix representation of  is called the matrix of
is called the matrix of  denoted by
denoted by . Recall that, if
. Recall that, if  is a field, then any vector space
is a field, then any vector space  of finite dimension
of finite dimension  over
over  is isomorphic to
is isomorphic to  . Therefore, any
. Therefore, any  matrix over
matrix over  can be considered as a linear operator on the vector space
can be considered as a linear operator on the vector space  in the fixed standard basis. Following this ideas, we study in this section, a rhotrix as a linear operator on the vector space
in the fixed standard basis. Following this ideas, we study in this section, a rhotrix as a linear operator on the vector space . Since the dimension of a rhotrix is always odd, it follow that, in representing a linear map
. Since the dimension of a rhotrix is always odd, it follow that, in representing a linear map  on a vector space
on a vector space  by a rhotrix, the dimension of
by a rhotrix, the dimension of  is necessarily odd. Therefore, throughout what follows, we shall consider only odd dimensional vector spaces. For any
is necessarily odd. Therefore, throughout what follows, we shall consider only odd dimensional vector spaces. For any  and
and  be an arbitrary field, we find the coupled
be an arbitrary field, we find the coupled of
of 
 and
and
 by
by

It is clear that  coincides with
coincides with  and so, if
and so, if , any n-dimensional vector spaces
, any n-dimensional vector spaces 
and 
 is of dimensions
is of dimensions  and
and  respectively. Less obviously, it can be seen that not every linear map
respectively. Less obviously, it can be seen that not every linear map  of
of  can be represented by a rhotrix in the standard basis. For instance, the map
can be represented by a rhotrix in the standard basis. For instance, the map

defined by

is a linear mapping on  which cannot be represented by a rhotrix in the standard basis. The following theorem characterizes when a linear map
which cannot be represented by a rhotrix in the standard basis. The following theorem characterizes when a linear map  on
on  can be represented by a rhotrix.
can be represented by a rhotrix.
4.1. Theorem
Let  and
and  be a field. Then, a linear map
be a field. Then, a linear map  can be represented by a rhotrix with respect to the standard basis if and only if
can be represented by a rhotrix with respect to the standard basis if and only if  is defined as
is defined as

where  and
and  are any linear map on
are any linear map on  and
and  respectively.
respectively.
Proof:
Suppose  is defined by
is defined by

where,  and
and  are any linear map on
are any linear map on  and
and  respectively, and consider the standard basis
respectively, and consider the standard basis
 . Note that, for
. Note that, for
 and
and . Since
. Since  are linear maps,
are linear maps, . Thus,
. Thus,
 (5)
(5)
Let  for
for
 and
and 
for . Then from (5), we have the matrix of
. Then from (5), we have the matrix of  is
is
 . (6)
. (6)
This is a filled coupled matrix from which we obtain the rhotrix representation of  as
as .
.
Conversely:
Suppose  has a rhotrix representation
has a rhotrix representation  in the standard basis. Then, the corresponding matrix representation of
in the standard basis. Then, the corresponding matrix representation of  is the filled coupled given in (6) above. Thus, we obtain the system
is the filled coupled given in (6) above. Thus, we obtain the system
 (7)
(7)
From this system, it follows that for each  we have the linear transformation
we have the linear transformation 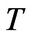 defined by
defined by

where,  and
and  are any linear map on
are any linear map on  with
with  for
for  and
and  for
for
 .
.
4.2. Example
Consider the linear mappings  define by
define by  To find the rhotrix of
To find the rhotrix of  relative to the standard basis. We proceed by finding the matrices of
relative to the standard basis. We proceed by finding the matrices of . Thus,
. Thus,

Therefore, by definition of matrix of  with respect to the standard basis, we have
with respect to the standard basis, we have

which is a filled coupled matrix from which we obtain the rhotrix of  in
in ,
, .
.
Now starting with the rhotrix  the filled coupled matrix of
the filled coupled matrix of  is
is .
.
And so, defining 

Thus, if 
Therefore,

5. Conclusion
We have considered the rank of a rhotrix and characterize its properties as an extension of ideas to the rhotrix theory rhomboidal arrays. Furthermore, a necessary and sufficient condition under which a linear map can be represented over rhotrix had been presented.
6. Acknowledgements
The Authors wish to thank Ahmadu Bello University, Zaria, Nigeria for financial support towards publication of this article.