Blow-Up and Attractor of Solution for Problems of Nonlinear Schrodinger Equations ()
1. Introduction
The quantum mechanics theory and application in more field in nature science. The non-linear Schrodinger equation is the basic equation in nonlinear science and widely applied in natural science such as the physics, chemistry, biology, communication and nonlinear optics etc. (See [1-9]) We study this equation to extend them are with important meaning (See[10-12]).
As we all know, the nonlinear Schrodinger equation be description quantum state of microcosmic grain by wave, it is variable for dependent time, and that is most essential equation, which position and action similarly Newton equation in position and action classics mechanics, it is apply to field as optics, plasma physics, laser gather, cohesions etc, particular on that action of power and trap, search analytical solution for Schrodinger equation is also difficult, and more so difficult for complicated power.
Now, we may extend some results in [4] by using Eigen-function method in through paper.
As we all know the solution of initial problem for Schrodinger equation bellow
 (1.1)
(1.1)
Assume that real part and imaginary part of

are real analytical function for  then this solution of the problem may expresses in form:
then this solution of the problem may expresses in form:

2. Several Theorems
In this section, we consider the blow-up of solutions to the mixed problems for higher-order nonlinear Schrodinger equation with as bellow.
It is well known the higher order equation:

where

that with new results for higher-order case. Now, we consider the blow-up of solutions to the mixed problems for six-order general Schrodinger equation to extend some results [4] that as bellow form:
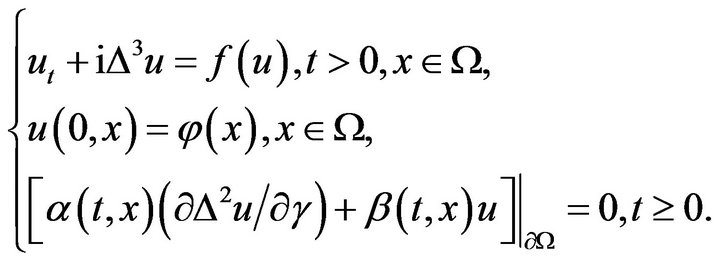 (2.1)
(2.1)
Assume that

not identical zero.
Where  holds complex value function with selfvariable for complex.
holds complex value function with selfvariable for complex.  is also complex value
is also complex value

Theorem 2.1. Suppose that nonlinear term  of problem (2.1) satisfy
of problem (2.1) satisfy ,
,

and  not identical zero then the classical solution of (2.1) must be for blow-up in finite time in
not identical zero then the classical solution of (2.1) must be for blow-up in finite time in

Proof. Let
 (2.2)
(2.2)
Then
 (2.3)
(2.3)
By the first Green’s formula, we have

Substituting it into (2.3), then

We may assume  then we have
then we have

Obviously, from  and
and 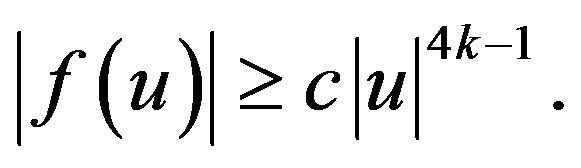 Therefore, we have
Therefore, we have
 .
.
By Schwartz inequality:

So,

Inductively, we have
 etc.,
etc.,

Then  increasing function similar in [4] from
increasing function similar in [4] from

and then there exists 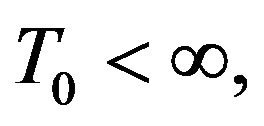 such that
such that  that is
that is

So, we complete the proof of this Theorem 2.1.
(As positive integer  we get it is theorem 3.1 in [4])
we get it is theorem 3.1 in [4])
Remark. Then we consider that important case is always for the Schrodinger equation may as bellow form
 .
.
Now, we shall consider also in this similar case:
 (2.4)
(2.4)
Therefore, we shall obtain the following theorem.
Theorem 2.2. Suppose that non-linear term  of problem (2.1) satisfy
of problem (2.1) satisfy ,
,

and

then the classical solution of (2.4) must be for blow-up in finite time in  (as positive
(as positive  then it is theorem 3.2 in [4]).
then it is theorem 3.2 in [4]).
Proof. Since 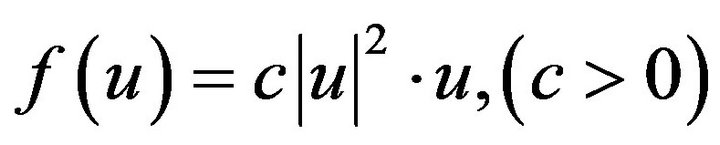 satisfies
satisfies
 then
then 
Thus, from theorem 2.1, we complete the proof of theorem 2.2.
Now, we shall give out the following theorem form. Here, we shall consider the problem:
 (2.5)
(2.5)
Theorem 2.3 Suppose that non-linear term  of problem (2.5) satisfy
of problem (2.5) satisfy
 ,
,
and

then the classical solution of (2.5) must be for blow-up in finite time in .
.
(As positive integer  then it is theorem 3.2 in [4])
then it is theorem 3.2 in [4])
Proof. Since  we have that
we have that

and

Thus, from theorem 2.1, we complete the proof of theorem 2.3. (As  it is theorem 3.3 in [4])
it is theorem 3.3 in [4])
Now, we may consider the following problem:
 (2.6)
(2.6)
where constant 
Theorem 2.4. Assume that  and
and 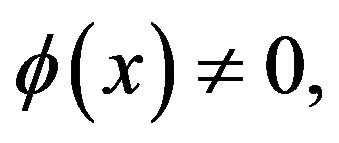 then the solution of (2.6) must be for blow-up in finite time in
then the solution of (2.6) must be for blow-up in finite time in .
.
Proof. From

then  satisfy
satisfy  and
and

It holds the condition of theorem 2.1, then by theorem 2.1 that we know the solution of problem (2.6) must be blow-up in finite time. Therefore, we complete the proof of theorem 2.4.
3. Main Results
We consider the initial boundary value of some higher order nonlinear Schrodinger equation. By using of eigenfunction method, we can get new results bellow.
Let

Furthermore, we will consider eight-order nonlinear Schrodinger equation. In first, stating that lemma 3.1.
Lemma 3.1. This Eigen-value problem (see [4])
 (*)
(*)
As we all know the first Eigen valu1e  of (*), the corresponding Eigen-function
of (*), the corresponding Eigen-function  assume it with
assume it with

Let  be bounded closed domain in
be bounded closed domain in 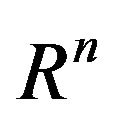 and by suite smooth conditions of function
and by suite smooth conditions of function  and
and  that from Green’s second formula, we easy get following results.
that from Green’s second formula, we easy get following results.
Now, we consider nonlinear Schrodinger equation with eight-order case 
 (3.1)
(3.1)
 (3.2)
(3.2)
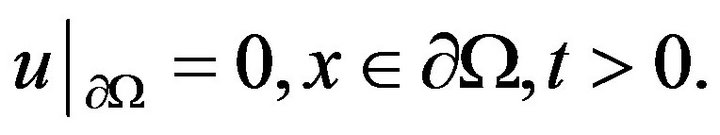 (3.3)
(3.3)
Clearly,  that is theorem 2.1 in [5].
that is theorem 2.1 in [5].
Theorem 3.1. Assume that problem (3.1)-(3.3) satisfy (where  out normal direction):
out normal direction):


 be continuous, convex and even function, here
be continuous, convex and even function, here


Then the classical solution of (4.1)-(4.3) must be blowup in finite time.
Proof. (I) step, when  and
and  In the similar way by [5] from that (4.1) first we take the real part of both sides for (4.1), we get that
In the similar way by [5] from that (4.1) first we take the real part of both sides for (4.1), we get that
 (3.4)
(3.4)
Multiplying by  the both sides of (3.4) and integral on
the both sides of (3.4) and integral on  for
for , it is form:
, it is form:

Taking 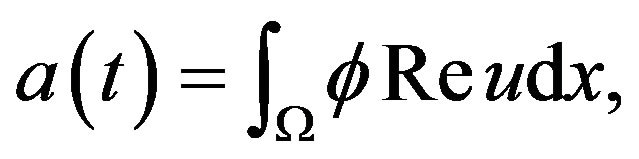 then
then 
and that
 (3.5)
(3.5)
By 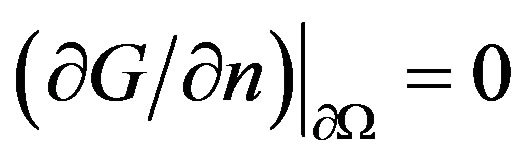 in (I) and Green’s second formula:
in (I) and Green’s second formula:
 (3.6)
(3.6)
Substituting (3.6) into (3.5), we get

Hence,
 (3.7)
(3.7)
From 

Therefore, we have
 (3.8)
(3.8)
Combing (3.7)-(3.8), and Jensen’s inequality, we obtain
 (3.9)
(3.9)
Here,  So,
So, 
there exist , such that
, such that
 (3.10)
(3.10)
From  and Holder inequality, we get
and Holder inequality, we get 

that is 
Therefore,

Hence,

(II) step, when  taking that
taking that

then 
Therefore, let we have
we have

Combine (4.1)-(4.8) and , we obtain that
, we obtain that
 (3.11)
(3.11)
That is also . From Jensen inequality and
. From Jensen inequality and  is even function, we have
is even function, we have

then
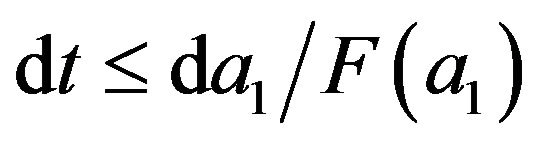 (3.12)
(3.12)
From (3.12) and similar (I)-step, we can get

Combine (I)-(II) we complete the proof of theorem 3.1.
Clearly,  that is theorem 2.1 in [5].
that is theorem 2.1 in [5].
Theorem 3.2. Assume that problem (3.1)-(3.3) satisfy:


and

where  is continuous, convex and even function;
is continuous, convex and even function;

Then the classical solution for this problem (3.1)-(3.3) is blow-up in finite time.
Proof. From  we discuss two case:
we discuss two case:

then 
Taking the imaginary part for both sides of (3.1), similar the method of proof for Theorem 3.1, we can easy have

So, we get that

(II)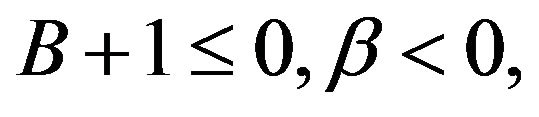 we may let
we may let  then
then 
So, 
Taking the imaginary part for both sides of (1), by (II) and similar the method of proof for theorem 3.1, we can easy have

We get that

Combine (I)-(II), we complete the proof of theorem 3.2.
Corollary 3.3. Clearly  that is theorem 2.2 in [5]. By ([13] )looking it for some applications.
that is theorem 2.2 in [5]. By ([13] )looking it for some applications.
4. Some Higher-Order Case
In the same way, we can consider the higher-order case (integer ):
):
 (4.1)
(4.1)
 (4.2)
(4.2)
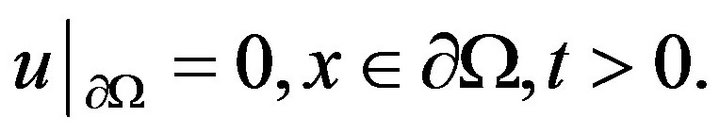 (4.3)
(4.3)
Clearly,  that is problem of eight order case.
that is problem of eight order case.
Theorem 4.1. Assume that problem (4.1)-(4.3) satisfy


and

where  is continuous, convex and even function;
is continuous, convex and even function;
 and
and 
Then the classical solution for this problem (4.1)-(4.3) is blow-up in finite time.(omit this similar proof )
Remark 4.2. Assume that (here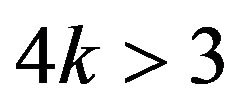 )
)

then we will obtain similar results of theorem 3.2 with more case.
Remark 4.3. (See [6,14]) According to the direction of [6], we may consider that coupled nonlinear Schrodinger equation as in the following iterative formulas in an algorithmic form by VIM:


The solution procedure with initial approximations (omit the details ):

The other components can be obtained directly:

Furthermore, the conserved quantities:

and
 where
where  This numerical results is with higher accuracy.
This numerical results is with higher accuracy.
5. The Global Attractor of the Fractional NSE
Recently, they also showed that dynamic behavior of large time action to investigate for [15,16], they are deepgoing study global attractor and dimension estimate of integer order non-linear Schrodinger equation in [16].
The author search the Cauchy problem for fractional order non-linear Schrodinger equation in [17]. The author search the global attractor problem for a class of fractional order non-linear Schrodinger equation in [17] and we based on [16-18], and combine [19] obtained the condition of existence of solution for following fractional order non-linear Schrodinger equation:
 (5.1)
(5.1)
Physics background of (1) is arise the main part of nonlinear interaction for laser and plasma,  express the field of electricity [20], where
express the field of electricity [20], where

is with standard perpendicular base, i is imaginary unit, the function 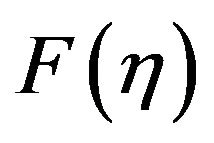 is with one order derivative
is with one order derivative  where
where  with some consume effect, and as
with some consume effect, and as  express the integral system with soliton solution.
express the integral system with soliton solution.
As  for (3.1), and (4.1) thirdly section case, we will obtain global attractor of initial value problem (5.1) that first give out Lemma as follows.
for (3.1), and (4.1) thirdly section case, we will obtain global attractor of initial value problem (5.1) that first give out Lemma as follows.
Lemma 5.1. Let

is the solution of problem (5.1), and
 (5.2)
(5.2)
Proof. Multiply  for the both sides of (**) act as inner product, we have
for the both sides of (**) act as inner product, we have
 (**)
(**)
and take real part,
 (5.3)
(5.3)
From (5.3) and by use of Gronwall inequality, we obtain

Lemma 5.2. Let

is the solution of problem (1), then 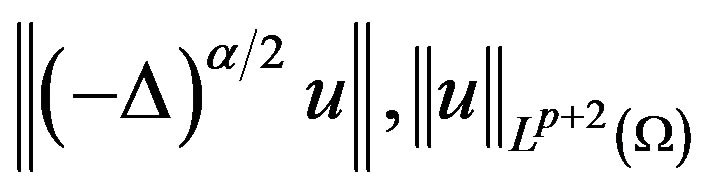 with uniform bounded.
with uniform bounded.
Proof. To establish inner product for both sides of equation (5.1) with for , and take real part, we have that
, and take real part, we have that

easy get that by (5.1),

where

by use of Jensen’s inequality, we have

So,

by use of Gronwall inequality, we obtain

uniform boundary.
Lemma 5.3. Let

is the solution of problem (5.1), then  with uniform bounded.
with uniform bounded.
Proof. To derivative both sides of Equation (5.1) for  and take inner product for
and take inner product for , and taking also imaginary part, we have
, and taking also imaginary part, we have

Then

By Lemma 5.2 and Young inequality, the (5.4) with form

by use of Gronwall inequality, we obtain

Because hold these inequality bellow

Hence  are uniform boundary. Similar method of [19,20], we give out that condition of yield global attractor of problem (5.1).
are uniform boundary. Similar method of [19,20], we give out that condition of yield global attractor of problem (5.1).
Theorem 5.4. Assume hat

then the periodic global attractor of initial value problem (4.1-4.3):

where  for operator semi-group with needing define in prove and
for operator semi-group with needing define in prove and for with the bounded attractor set in following in prove processes.
for with the bounded attractor set in following in prove processes.
Proof. We omit the proof (by using of similar proof method in [18,19]).
Remark 5.5. Furthermore, we shall study global attractor of fraction order non-linear Schrodinger type equation, and the estimate for its dimensions, and that blowing-up of solution for some fraction order non-linear Schrodinger type equation.
6. Some Notes for Shake Power and Light Power
Atoms absorb energy from the ground state transition to the excited state, learned through experiments in extreme case, the ground state solution is not controlled solution-Blow-up solution.
Thus, strictly control the number and perturbation for impulsive velocity of the atomic transition, is one of the main methods to produce new material structure. Strict control of the atomic transition to the first, second and third excited state is more practical significance, especially the transition to the first excited state. As we all now, the ultra-low temperatures, the atomic gas in the magnetic potential well Boer-Einstein condensation experiments [21], promotion of scholars study the macroscopic quantum behavior of atoms and kinetic characteristics.
By using of above stating method we consider calculate to the ground state solution and excite state of ddimension BECS (Bose-Einstein condensate) with mix harmonic potential and crystal lattice potential.
The Gross-Pitaevskii equation:
 (6.1)
(6.1)
where 
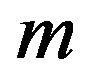 expresses mass of atoms,
expresses mass of atoms,  be planck constant,
be planck constant,  be number of atoms in cohesion system,
be number of atoms in cohesion system,  be outer power,
be outer power,
 describe interaction between the atoms cohesion (
describe interaction between the atoms cohesion (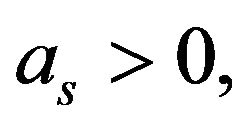 means repel;
means repel;  shows attract each other). Thus, by pass appropriate immeasurable process, then the (6.1) may be written:
shows attract each other). Thus, by pass appropriate immeasurable process, then the (6.1) may be written:
 (6.2)
(6.2)
The parameter  for positive, or negative, describe that repel or attract corresponding, out power
for positive, or negative, describe that repel or attract corresponding, out power  be defined by physic system for us to study things. By using of the imaginary time method to calculate it in [22] that let
be defined by physic system for us to study things. By using of the imaginary time method to calculate it in [22] that let 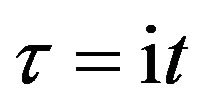 substituting it into (6.2), we have
substituting it into (6.2), we have
 (6.3)
(6.3)
So, by check parameter method in [23] we check nonlinear parameter for light rule power, then we get ground state and excite state correspondingly.
6.1. One Dimension Case (d = 1)
 We consider two class powers (shake power and light power) in (6.3), Setting shake power
We consider two class powers (shake power and light power) in (6.3), Setting shake power

taking initial wave
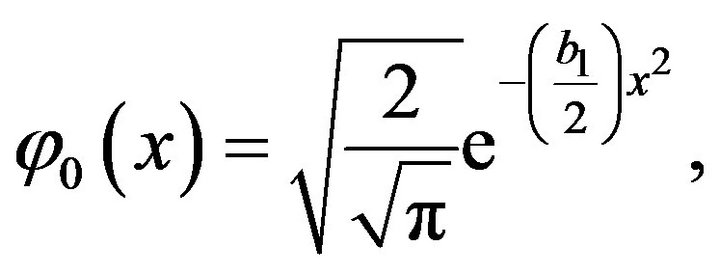 (6.4)
(6.4)
to calculate ground state  For (6.4) we calculate first arouse state
For (6.4) we calculate first arouse state 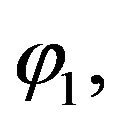 space field for
space field for  the time step for
the time step for 
 Similar above way, taking
Similar above way, taking

and (6.3) for

and  and
and 
On the other hand, by the MATLAB search the solution of Equation (6.3) in case (1) and (2) as follow with  (See Figures 1 and 2).
(See Figures 1 and 2).
6.2. Two-Dimension Case (d = 2)
Consider shake power in [14,24]

Figure 1. Ground state phi0. First excited state phi1. V = x2/2; b = 500, bi = 2.

The grain energy:

We take initial wave function for

To calculate ground state ; For
; For


and

 .
.
By calculating 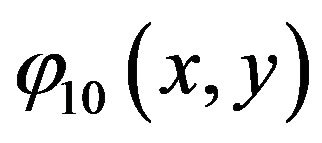 along the direction of axe
along the direction of axe  and
and  in direction of axe y, and calculating first excited of
in direction of axe y, and calculating first excited of  along direction for axe x and axe y, and space field for
along direction for axe x and axe y, and space field for  time step:
time step:

Combine these cases as Fig: (See Figures 3(a) and (b), Figures 4-6)

Figure 2. Ground state phi0. First excited state phi1. V = x2/2 + 25*(sin(pi*x/4))2; b = 500, bi = 2.
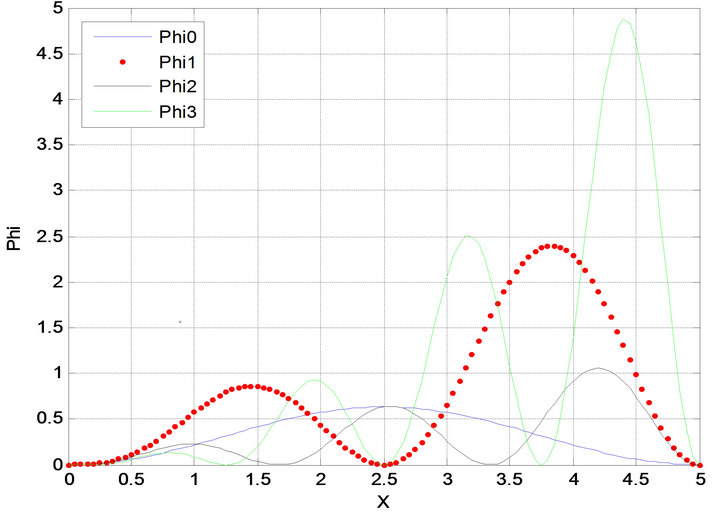 (a)
(a) (b)
(b)
Figure 3. (a) Ground state phi0. First excited state phi1. a = 5, b = 2. (b) Ground state phi0. First excited state phi1. a = 5, b = 2.

Figure 4. Ground state phi0 a = 5, b = 2.

Figure 5. First excited state phi1-x a = 5, b = 2.

Figure 6. First excited state phi2-y a = 5, b = 2.

Figure 7. First excited state phi3-xy a = 5, b = 2.
We consider three-dimension case, Figure 4 for ground state  corresponding case, the
corresponding case, the 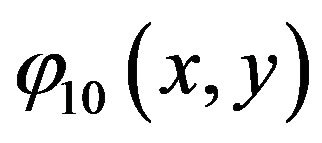 as with express along direction of axe x (wave surface) in Figure 5, the
as with express along direction of axe x (wave surface) in Figure 5, the  as with express along direction of axe y (wave surface) in Figure 6, the
as with express along direction of axe y (wave surface) in Figure 6, the 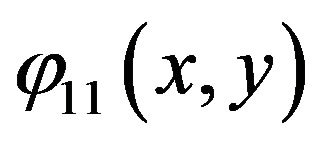 as for express along direction of axe x and axe y (wave surface) in Figure 7.
as for express along direction of axe x and axe y (wave surface) in Figure 7.
7. Concluding Remarks
Recently, the higher-order Schrodinger differential equations is also a very interesting topic, and that application of some physics and mechanics of for some more fields as nonlinear Schrodinger equations and some compute methods etc. In our future work, we may obtain some better results.
The application of some physics and mechanics of for some more fields with some combine equations (look [7, 13]).
8. Acknowledgements
This work is supported by the Nature Science Foundation (No.11ZB192) of Sichuan Education Bureau (No.11zd 1007 of Southwest University of Science and Technology).
NOTES
*Corresponding author.