1. INTRODUCTION
The integration of reaction and separation of the corresponding products in solid-liquid reactors allows, in addition to obvious savings in equipment costs, significant improvements in the process performance. Typical reactor examples of that type include moving bed reactors.
The solid-liquid contact in a moving bed reactor might occur, either in a co-current or a counter-current mode. Common examples of counter-current moving bed are inclined and vertical kilns and transport reactors. Similar to other fluid-solid reactors, the global kinetics of the reactor is determined by mass transfer from the bulk fluid to the interior of the solid phase and/or by the chemical reaction. Generally, the internal mass transfer inside the solid particle offers much greater resistance than other steps [1-5], so that it can be considered as the rate-determining step.
Selective separation of metal ions from aqueous solutions might be carried out through solvent-impregnated resin (SIR) [6-8], which efficiently extracts solute ions from dilute liquors. This resin type, in specific, has a high distribution ratio and a high selectivity for extractants dissolved in a liquid organic phase. It also exhibits strong affinity for the polymeric matrix though behaving as if it were in the liquid state [8-10]. Some studies showed that the impregnated resins, prepared by the adsorption of a bi-functional extractant onto large surface macroporous supports of Amberlite XAD2, are successfully used for the extraction of Zn2+, Cu2+ and Cd2+ ions [11,12]. Former studies were devoted to the impregnation processes, the physico-chemical characterization of resins, the description of the extraction reactions, or the selectivity patterns. However, the application of these systems in a fixed column or fluidized bed technology requires information of the equilibrium and kinetics of the metal extraction processes and the hydraulic operating behaviour. In the present study a mathematical model describing the behaviour of a counter-flow moving-bed reactor is proposed analogous to those formerly suggested for a batch and a fixed bed reactor [3,5]. This study may help in suggesting proper design and operation conditions in order to scale-up the overall process.
2. EXPERIMENTAL
2.1. Reagents
The chemicals used in this study are of analytical grade (Merck A.R. grade) and are used as received. Stock solutions of Zn(II), Cu(II) and Cd(II) (1 g/L) are prepared by dissolving the corresponding nitrate salt in water. The used Amberlite XAD-2 resin is supplied by Rohm and Haas with 0.3 - 0.9 mm size. O-methyl-dihexyl-phosphine-oxide-O’-hexyl-2-ethyl phosphoric acid (HL) with purity higher than 98% is used. The SIR resins are prepared as previously described [11,12].
2.2. Sorption Kinetics
In the study the shallow bed technique on a micro scale is used where an aqueous metal solution is passed at a high flow-rate through a micro column of the resin bed [12-15]. The flow of the metal solution is stopped and the resin is washed with water and the resin compositions are analyzed to provide data about metal concentration as function of time. Micro columns around 2.5 mm depth are used and the employed flow-rate is 0.2 L/h. The pH of the metal solutions is maintained around 5 by adding NaOH. All kinetic measurements are carried out at room temperature.
The metal ions concentrations are determined by elution using 0.2 M hydrochloric acid solution. After dilution, the metal ions are analyzed by inductively atomic emission spectro-photometry using an ICP-AE JY-138 Ultratrace. The metal ions concentrations results are expressed as mol/kg of dry SIR.
3. MODEL DEVELOPMENT
The sorption of metal ions on solvent impregnated resin in a counter flow moving bed reactor can be considered analogous to fluid-solid noncatalytic reactions. Such a reaction occurs by the adsorption of the fluid reactant at an active site on the solid followed by a chemical reaction involving the adsorbate ion and the solid reactant. In a former study of S. Othman et al. [3] the diffusion rate, expressed as the number of moles adsorbed (N) per unit time (t) per particle, was suggested to be proportional to , where KD is a diffusion parameter with a dimension of s–1. Two categories of diffusion parameters were discriminated; external diffusion parameter, which describes the diffusion through the aqueous boundary layer to the outermost resin layer
, where KD is a diffusion parameter with a dimension of s–1. Two categories of diffusion parameters were discriminated; external diffusion parameter, which describes the diffusion through the aqueous boundary layer to the outermost resin layer , and diffusion through the adsorbed layers
, and diffusion through the adsorbed layers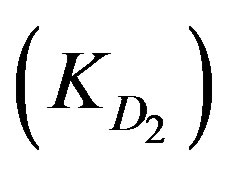 . As the adsorption kinetics is largely limited by the internal diffusion step [3,5],
. As the adsorption kinetics is largely limited by the internal diffusion step [3,5],  is likely found to be greater than
is likely found to be greater than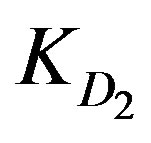 . Accordingly, the following two diffusion-type equations were proposed [3].
. Accordingly, the following two diffusion-type equations were proposed [3].
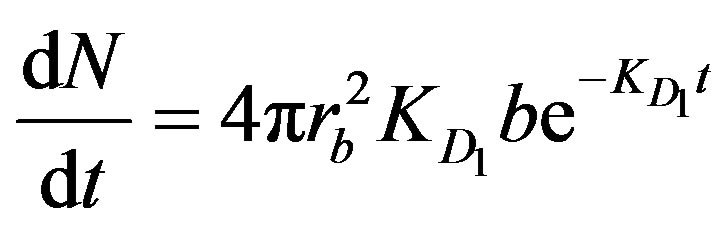 (1)
(1)
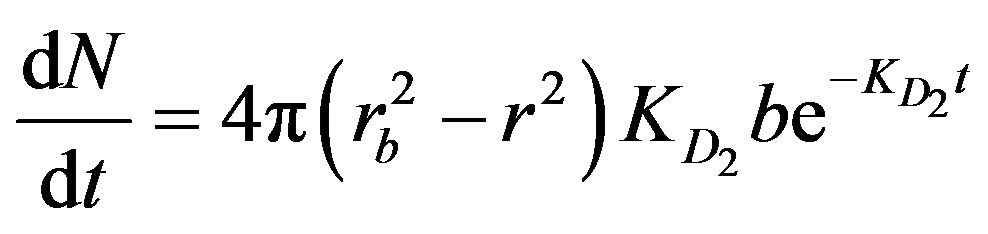 (2)
(2)
where N is the number of moles of product formed per unit time (t) per particle, rb is the radius of the boundary layer, and b (mole/m2) signifies the number of active sites available per unit surface area.
A third equation due to chemical reaction considering a pseudo-first order rate equation was also proposed [3, 5].
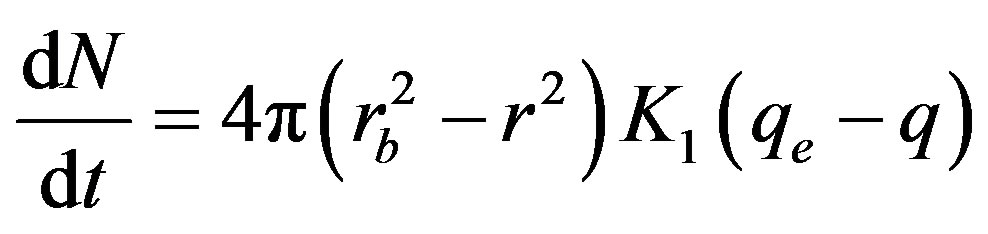 (3)
(3)
where K1 (kg·m–2·s–1) is the chemical reaction rate parameter. The constant qe (mol/kg) is the equilibrium concentration of the product; i.e. the concentration of metal ion at the end of the moving bed reactor and q (mol/kg) is the concentration of metal ion per unit mass of resin along the reactor height.
By applying steady state approximation, the two diffusion equations were equated resulting in a relation giving the variation of the un-reacted core radius in terms of time. Substituting this relation in the chemical reaction equation gives the following relation [3,5].
 (4)
(4)
The variation of the number of adsorbed moles produced with time was converted into the rate of change of adsorbed ion concentration per unit resin mass 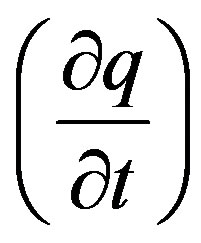
giving the following differential relation [3,5]:
 (5)
(5)
where  is the resin-specific reaction rate parameter in s–1.
is the resin-specific reaction rate parameter in s–1.
According to the boundary conditions of a moving bed-type reactor (q = 0 at t = 0) the above equation can be integrated giving the following reaction [3]:
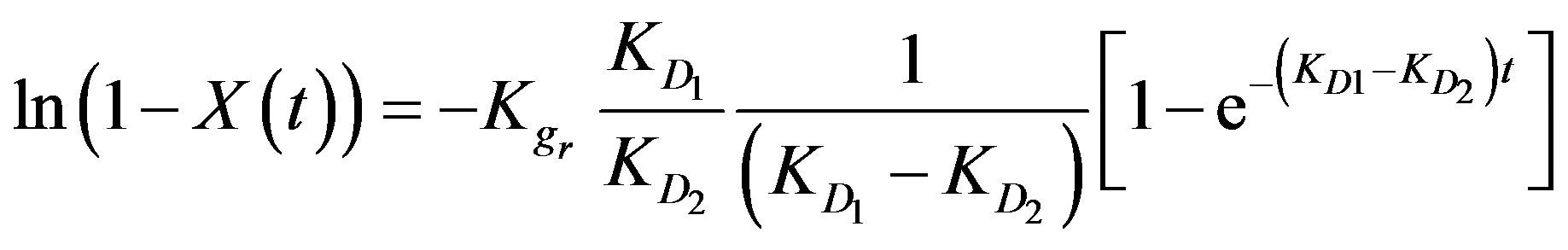 (6)
(6)
However, in this type of reactor (moving bed reactor), the concentration of reactant and product varies with position. Hence, the properties at any height in the bed do not change with time. Figure 1 is a schematic representation of the model considered for this analysis. Under these conditions the residence time is the same for all resin particles. It is related to an elemental height of the reactor length, Dz, through the following expression:
 . (7)
. (7)
Accordingly,
 (8)
(8)
where es is the fractional holdup of solids (fraction of
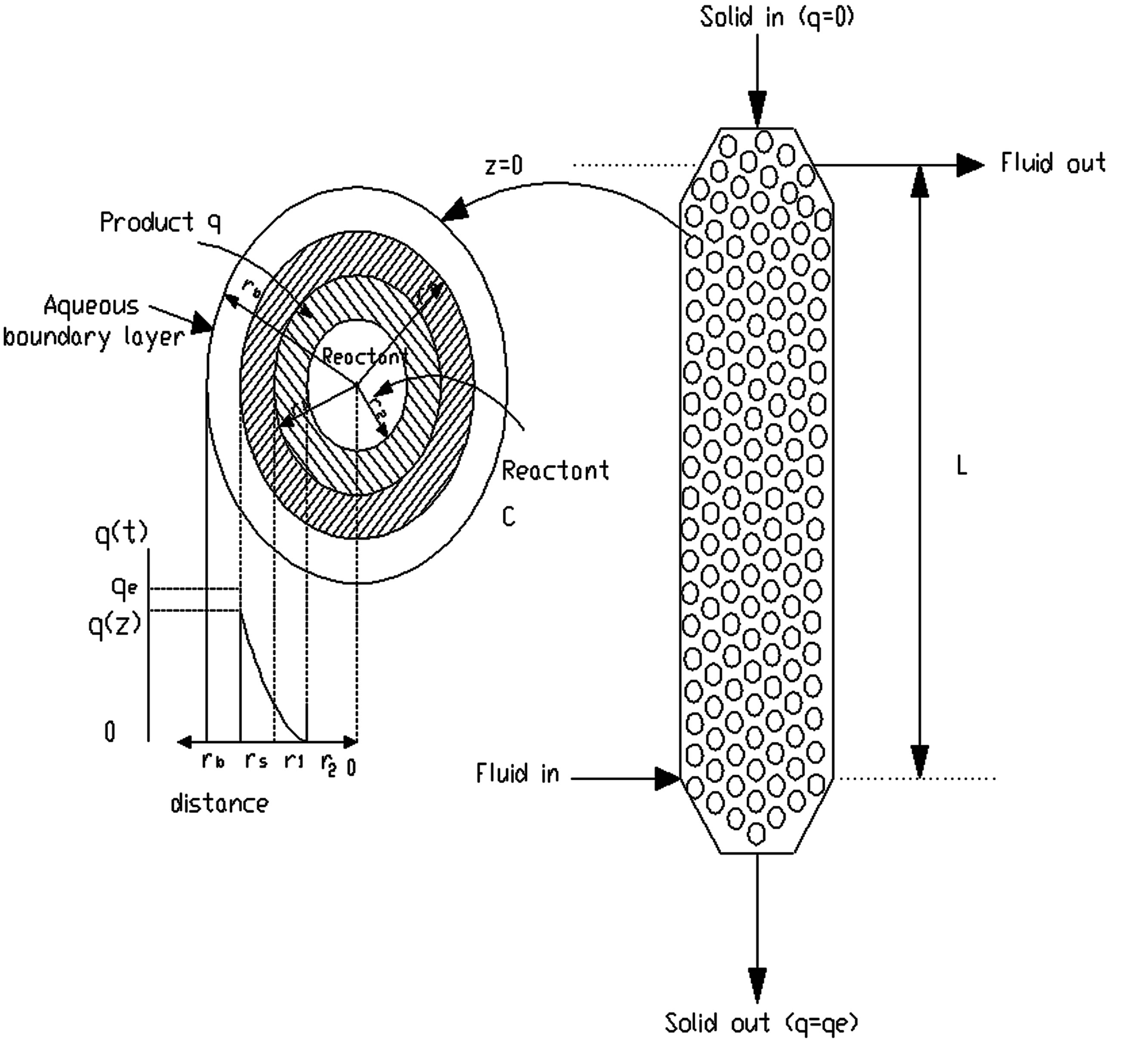
Figure 1. Schematic representation of the model development.
reactor volume occupied by solids), Ac is the cross-sectional area of resin column, and rp is the density of the resin and z is the vertical distance of reactor length starting from the solid entrance.
Thus
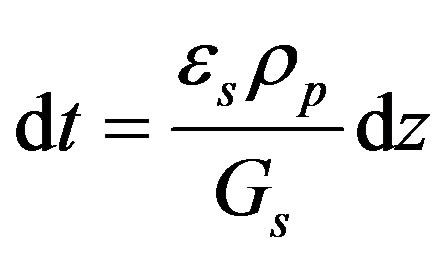
where Gs is the superficial mass velocity of solids at z, kg/(m2·s). The relation between the reactor height and the time is thus linear.
Transforming thus  to a differential of
to a differential of  by multiplying the former by
by multiplying the former by , considering Eq.6 and
, considering Eq.6 and  then the following equation could be obtained:
then the following equation could be obtained:
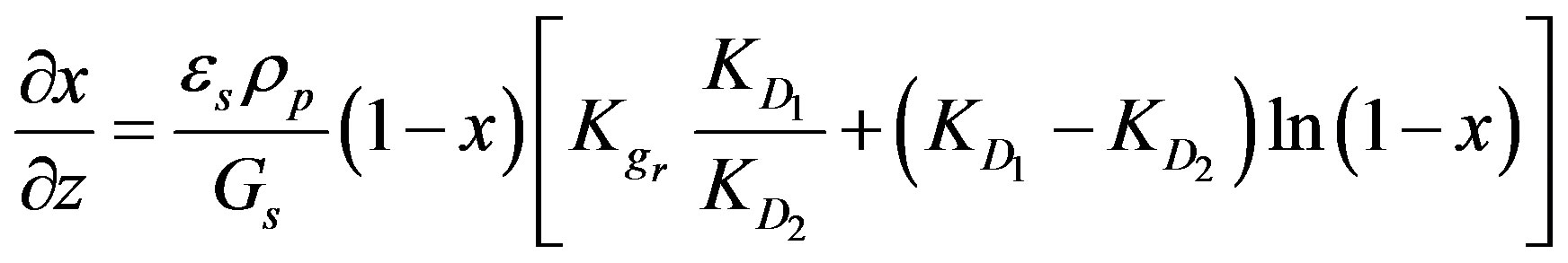 (10)
(10)
To estimate the required reactor height that yields a conversion of xL the above equation can be written in the following limited integration form:
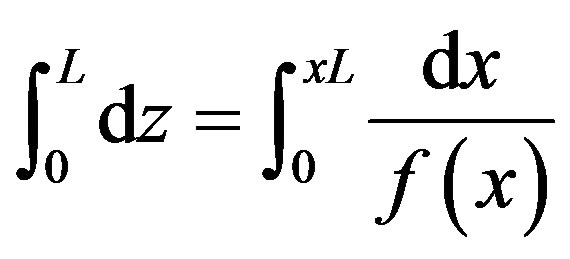 (11)
(11)
Integrating this equation by considering the boundary conditions that x = 0 at z = 0 and z = L at x = xL the following equation could be obtained:
 (12)
(12)
where n is the “relative resin velocity factor” (m/s) which is the linear velocity of the resin particles inside the reactor related to the fraction of reactor occupied by resins and equal  .
.
The diffusion parameter difference  is the difference between external and internal diffusion parameters and equals
is the difference between external and internal diffusion parameters and equals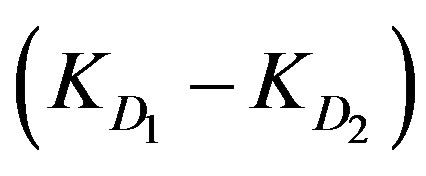 . The diffusion parameter ratio,
. The diffusion parameter ratio,  , gives the ratio of internal to external diffusion parameters.
, gives the ratio of internal to external diffusion parameters.
4. THEORETICAL STUDY
The model parameters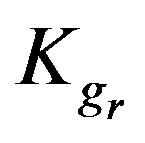 ,
,  and
and 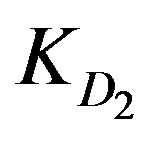 indicate whether the process is controlled by chemical reaction, by external, or internal diffusion [3,5]. The rate-controlling mechanism can be the diffusion through the aqueous boundary layer to the outermost resin layer (external diffusion) or diffusion inside the particle (internal diffusion). The resin ion-exchange processes are normally considered to be diffusion controlled and not reaction controlled [1-5]. When
indicate whether the process is controlled by chemical reaction, by external, or internal diffusion [3,5]. The rate-controlling mechanism can be the diffusion through the aqueous boundary layer to the outermost resin layer (external diffusion) or diffusion inside the particle (internal diffusion). The resin ion-exchange processes are normally considered to be diffusion controlled and not reaction controlled [1-5]. When  ratio is high, the internal diffusion dominates and is the rate determining step so that
ratio is high, the internal diffusion dominates and is the rate determining step so that .
.
The same approach can be applied for other types of control. It should be noted that this ratio is constant for the same reaction condition; i.e. the same solution, the same solid reactant, etc. Diffusion easiness might vary by varying the process condition.
4.1. Effect of Relative Resin Velocity Factor
The value of n may be increased by either increasing the superficial resin velocity; i.e. the amount of resin flowing per unit cross sectional area per unit time, or by either decreasing the resin density or the fractional holdup of solids in the reactor. This in turn means either higher resin velocity (i.e. smaller contact time between solute and resin) or the presence of fewer resin particles in the column in a specific time so that less ions will be adsorbed on the resin surface. This is shown in Figure 2 as the conversion extent decreases with increasing the relative resin velocity factor, which in turn requires larger column height. For example at a four-meter column height the estimated percentage conversion reached with a relative resin velocity factor of 7.1 × 10−3 m/s is 33.4%, while a ten-time higher velocity factor yields a low conversion of only 4.2%. Increasing the factor ten times more gives an even much lower conversion of 0.43%.
It is to be noted that the residence time of the resins in the reactor is inversely proportional to the relative resin velocity factor so that an increase in the factor causes a reduction in the residence time; i.e. less contact time between the resin particle and the solute ions. This negatively affects the adsorption of ions on the resin particles.
4.2. Effect of Diffusion Parameter Difference
Figure 3 shows that increasing the diffusion parameter difference, 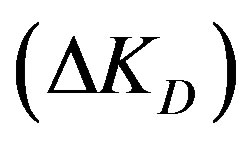 , reduces the conversion extent and a longer reactor is required. With a larger difference lower adsorption is obtained at the same bed height. However, when the variation of this difference is maintained within low enough values the effect is minimized. This observation is similar to that obtained with a fixed bed. For example at a reactor height of 4 m the percentage conversion obtained with a difference of 2 × 10–3 is 22.8%. Lowering the difference by a tenth (2 × 10–4) increases the conversion to 33.4%. A further reduction of the difference to 2 × 10–5 gives a smaller increment of the adsorption extent to a value of 34.8%. If the reactor height is increased to 1.5 the value (6 m) the conversion increases to 44.7% with a difference of 2 × 10–4. A reduction of the difference by a tenth slightly increases the conversion to 47.2% whereas a further increase of the former value by a tenfold (2 × 10–3) leads to a significantly lower conversion of 26.8%. This observation contradicts the findings of a former study in a fixed bed reactor as larger diffusion difference offered higher adsorption [5]. Accordingly, in a moving bed reactor the difference between external and internal diffusion parameters should thus be kept as small as possible for effective adsorption and practical reactor height. This difference can be increased by either increasing only the value of external diffusion parameter or increasing both internal and external diffusion parameters with the same proportion.
, reduces the conversion extent and a longer reactor is required. With a larger difference lower adsorption is obtained at the same bed height. However, when the variation of this difference is maintained within low enough values the effect is minimized. This observation is similar to that obtained with a fixed bed. For example at a reactor height of 4 m the percentage conversion obtained with a difference of 2 × 10–3 is 22.8%. Lowering the difference by a tenth (2 × 10–4) increases the conversion to 33.4%. A further reduction of the difference to 2 × 10–5 gives a smaller increment of the adsorption extent to a value of 34.8%. If the reactor height is increased to 1.5 the value (6 m) the conversion increases to 44.7% with a difference of 2 × 10–4. A reduction of the difference by a tenth slightly increases the conversion to 47.2% whereas a further increase of the former value by a tenfold (2 × 10–3) leads to a significantly lower conversion of 26.8%. This observation contradicts the findings of a former study in a fixed bed reactor as larger diffusion difference offered higher adsorption [5]. Accordingly, in a moving bed reactor the difference between external and internal diffusion parameters should thus be kept as small as possible for effective adsorption and practical reactor height. This difference can be increased by either increasing only the value of external diffusion parameter or increasing both internal and external diffusion parameters with the same proportion.
4.3. Effect of Diffusion Parameter Ratio
Increasing the ratio of the diffusion parameters 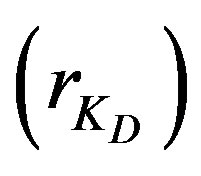
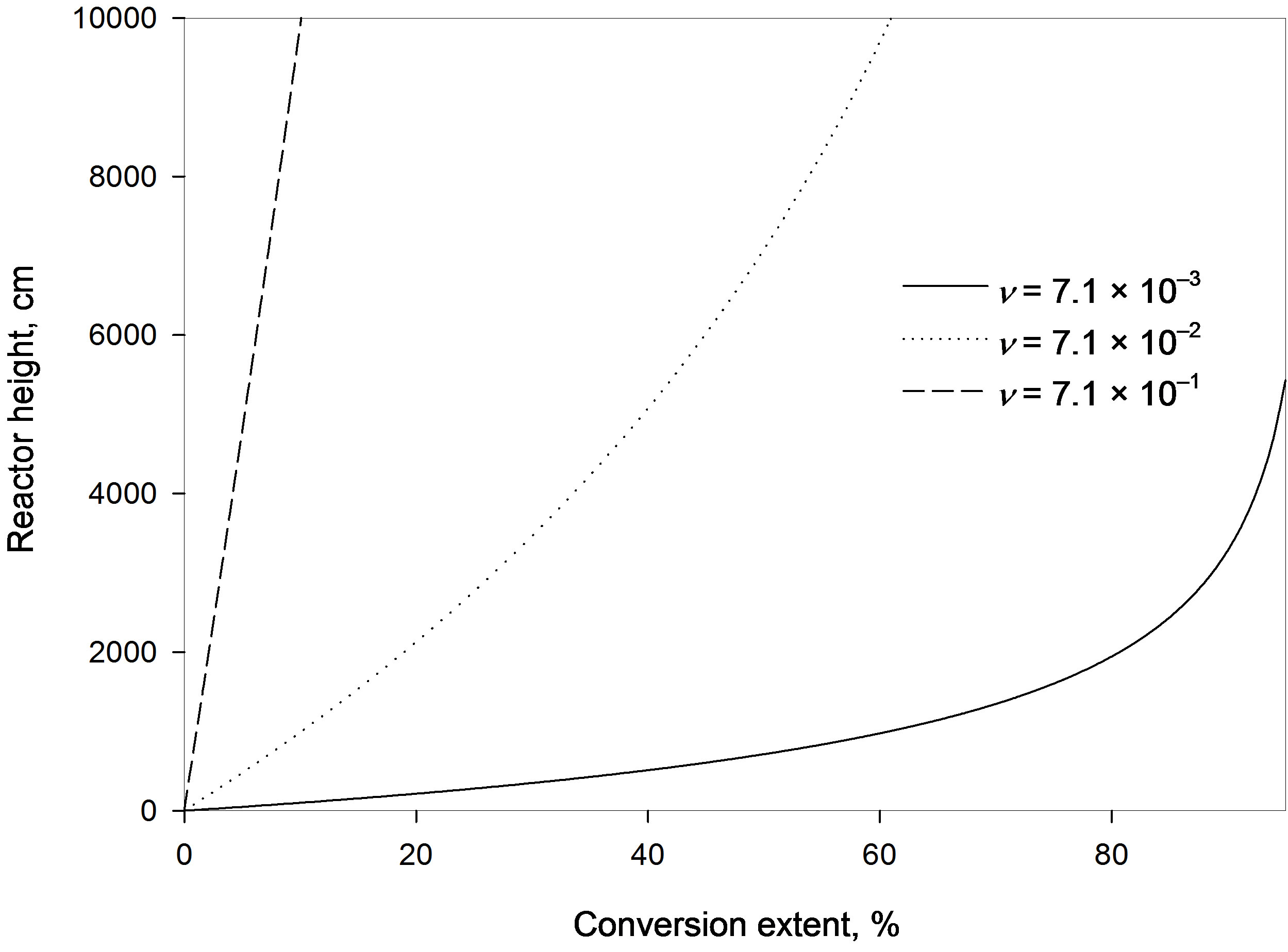
Figure 2. The effect of relative resin velocity factor.
has the same effect as increasing the difference of diffusion parameters, as the adsorption efficiency decreases and an appreciable increase in the reactor height is needed. This is shown in Figure 4, where for example at a 4-meter height the conversion increases nearly ten times by reducing the ratio by ten folds. With a ratio of 75 the conversion is only 0.4% while it is 4% with a ratio of 7.5. At a ratio of 0.75 the conversion is much higher (33.4%). These observations are again contradicting to those obtained in a fixed bed reactor [5] as a larger ratio was found to increase the column efficiency and the adsorbate ions get adsorbed at a shorter distance.
4.4. Effect of Resin-Specific Reaction Rate Parameter
The resin-specific reaction rate parameter can be largely increased by using smaller resin particles [2]. Figure 5 shows that increasing the resin-specific reaction rate parameter largely increases the conversion extent and reduces the required reactor height. At a short column depth of only 25 cm the conversion is low (2.6%) with a  value of 6 × 10–4. However, increasing the
value of 6 × 10–4. However, increasing the 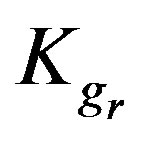 value ten times (6 × 10–3) greatly increases the conversion to 24%. A further similar increase of the
value ten times (6 × 10–3) greatly increases the conversion to 24%. A further similar increase of the  value to 6 × 10–2 gives a conversion extent as high as
value to 6 × 10–2 gives a conversion extent as high as
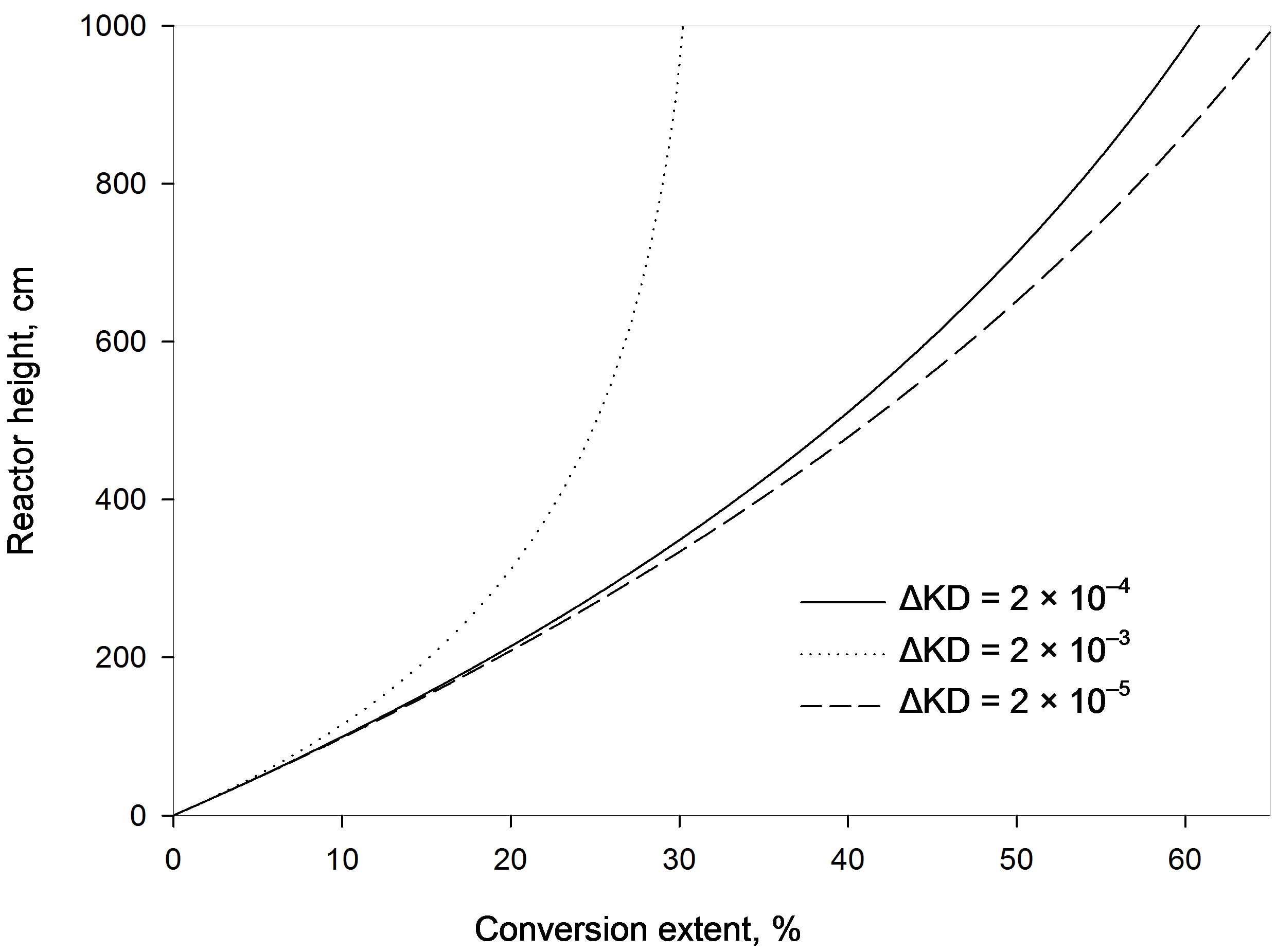
Figure 3. The effect of diffusion parameter difference.
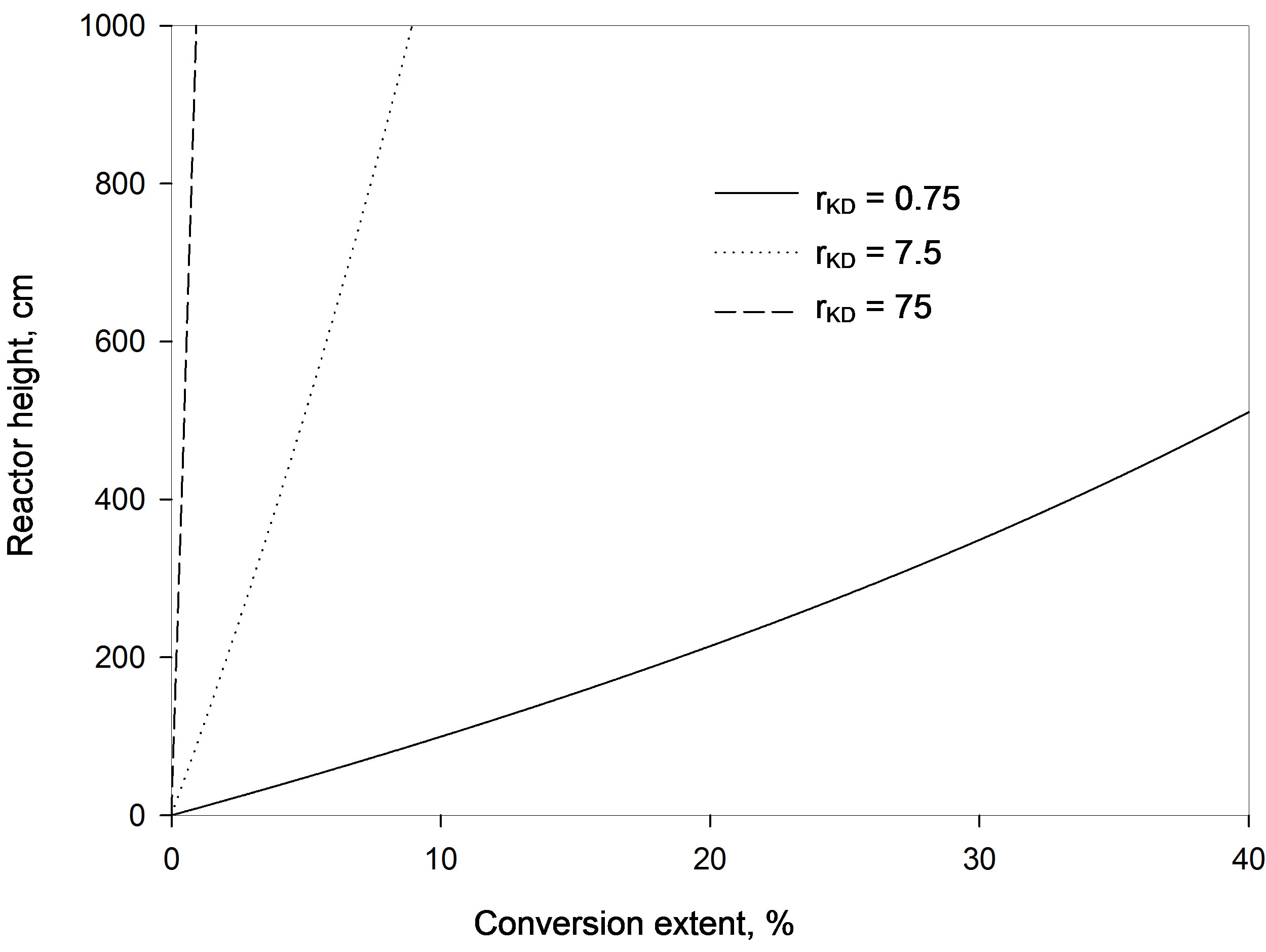
Figure 4. The Effect of diffusion parameter ratio.
93.8%. A slight variation of the  value provides thus an effective impact on the conversion extent, which can be reasonably understood as this parameter includes the reaction rate constant that is responsible for the speed of reaction. These findings agree with those obtained by Othman et al. [1-5].
value provides thus an effective impact on the conversion extent, which can be reasonably understood as this parameter includes the reaction rate constant that is responsible for the speed of reaction. These findings agree with those obtained by Othman et al. [1-5].
5. EXPERIMENTAL STUDY
Table 1 includes the regression analysis of Eq.6 for series of experiments together with the estimated relative values of ,
, 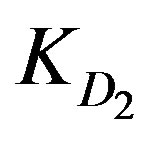 and
and 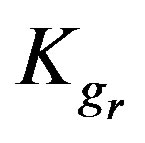 for the current model concerning two different concentrations of a single metal ion solution; high (1 × 10–2 M) and low (1 × 10–4 M) concentration. It is observed for the three metal ions that the chemical reaction is controlling for both concentrations as
for the current model concerning two different concentrations of a single metal ion solution; high (1 × 10–2 M) and low (1 × 10–4 M) concentration. It is observed for the three metal ions that the chemical reaction is controlling for both concentrations as . These results can be attributed to the applied experimental conditions where shallow-bed technique on a micro scale is used. In this technique an
. These results can be attributed to the applied experimental conditions where shallow-bed technique on a micro scale is used. In this technique an
aqueous metal solution is passed at a high flow-rate through a thin layer of resin beads in a column. The objective of this procedure is to avoid the formation of a concentration gradient along the bed, either in the resin or in the solution. Thus, the solution composition remains practically constant throughout the experiment. Accordingly, the shallow bed technique simulates the operation conditions of industrial moving beds.
5.1. Sorption Kinetics at High Concentration
This series of experiments are run at a relatively high concentration (1 × 10–2 M) with the purpose of promoting internal diffusion control. The first hour of the process is studied in this experiment. The correlations indicate a good fit for Eq.12. A comparison of the model parameters shows that there are significant differences in diffusivity for the three metal ions. For the high concentration (1 × 10–2 M), the relative order of diffusivity in

Figure 5. The Effect of resin-specific reaction rate parameter.
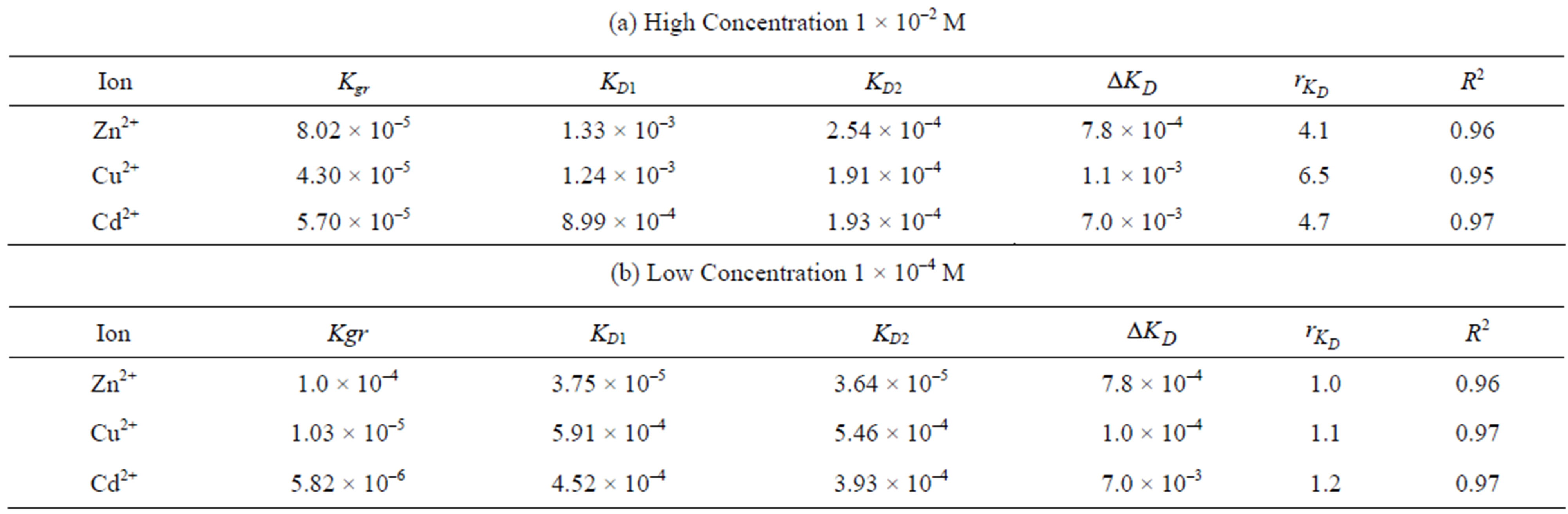
Table 1. The physical parameters for the three cations in high and low solution concentrations.
the solution is: Zn2+ > Cu2+ > Cd2+. Accordingly, Cd2+ solution has the highest diffusion parameter difference,  , followed with Cu2+ followed with Zn2+, which has the lowest difference as well as the lowest diffusion parameter ratio.
, followed with Cu2+ followed with Zn2+, which has the lowest difference as well as the lowest diffusion parameter ratio.
Figure 6 shows the results of the extraction kinetics of Zn2+, Cu2+ and Cd2+ from single element solutions in the form of the suggested model defined by Eq.12. The theoretical results give satisfactory agreement to those obtained experimentally. As the resin-specific reaction rate parameter is the most affecting in the adsorption extent, as shown in the theoretical study, Zn2+ yields the highest conversion extent followed by Cd2+ followed by Cu2+ although the corresponding values differ only slightly from each other. This observation fits well with the decreasing tendency of the  values, which again supports the findings that
values, which again supports the findings that 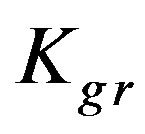 plays a significant effective role in the conversion extent (Figure 5).
plays a significant effective role in the conversion extent (Figure 5).
5.2. Sorption Kinetics at Low Concentration
For Zn2+ and Cu2+ solutions the KD values are appre-
 (a)
(a) (b)
(b)
Figure 6. Comparison between the conversion extents obtained for the three low concentrated (1 × 10–4 M) metal ion solutions with respect to (a) reactor height and (b) time.
ciably lower than the corresponding ones for high concentrations indicating poorer adsorption in both the solution and resin particles due to the lower concentration. However, the corresponding diffusion parameter differences in low as well as high concentrations are the same for the three solutions indicating that the KD values decrease with the same amount. On the other hand, the diffusion parameter ratios are nearly the same for the three solutions. For Cu2+ and Cd2+ solutions the  values are significantly lower than the corresponding ones at high concentration. However, the
values are significantly lower than the corresponding ones at high concentration. However, the  value for the Zn solution is higher than the corresponding one at high solution concentration.
value for the Zn solution is higher than the corresponding one at high solution concentration.
In the current case  is bigger than
is bigger than  indicating a much smaller difference than that observed at higher concentration indicating that both external and internal diffusion find comparable resistance. The
indicating a much smaller difference than that observed at higher concentration indicating that both external and internal diffusion find comparable resistance. The  values for Cu2+ and Cd2+ are found to be significantly smaller than both
values for Cu2+ and Cd2+ are found to be significantly smaller than both 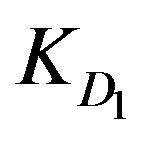 and
and 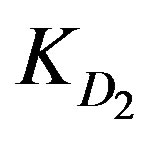 indicating a chemical reaction control. Figure 7 shows the conversion extent (x) as a function of contact time as yielded experimentally and theoretically at low concentration of the three metal ions (Zn2+, Cu2+ and Cd2+). The figure shows that Zn2+ yields the highest conversion extent followed by Cu2+ followed by Cd2+. This is again in full agreement with the incremental trend of the
indicating a chemical reaction control. Figure 7 shows the conversion extent (x) as a function of contact time as yielded experimentally and theoretically at low concentration of the three metal ions (Zn2+, Cu2+ and Cd2+). The figure shows that Zn2+ yields the highest conversion extent followed by Cu2+ followed by Cd2+. This is again in full agreement with the incremental trend of the  values of the corre-
values of the corre-
 (a)
(a) (b)
(b)
Figure 7. Comparison between the conversion extents obtained for the three highly concentrated (1 × 10–2 M) metal ion solutions with respect to (a) reactor height and (b) time.
sponding salts.
It is observed from Table 1 that the highest 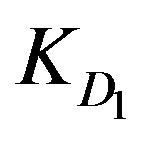 and
and 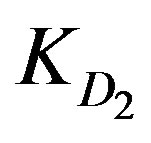 values are provided with Zn2+ ions in the highly tested solution concentration whereas Cd2+ ions offer the least
values are provided with Zn2+ ions in the highly tested solution concentration whereas Cd2+ ions offer the least  value. This is nearly the same for
value. This is nearly the same for  values since Cd2+ and Cu2+ ions have almost the same
values since Cd2+ and Cu2+ ions have almost the same 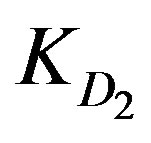 values. However, the high ranking of Zn2+ ions turns to be opposite in case of low solution concentration as Zn2+ yields the least
values. However, the high ranking of Zn2+ ions turns to be opposite in case of low solution concentration as Zn2+ yields the least 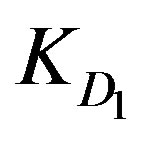 and
and  values, whereas Cu2+ ions provide the highest diffusion parameter values.
values, whereas Cu2+ ions provide the highest diffusion parameter values.
In both solution concentrations Zn2+ ions yield the lowest  and
and 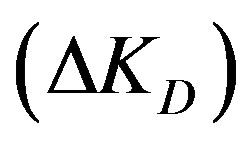 values and the highest
values and the highest 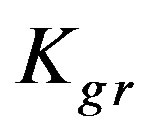 values. It is not worthy that the
values. It is not worthy that the 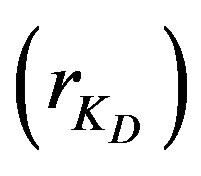 values in case of low concentrations are almost the same around unity with a slight variation while they differ appreciably in case of high concentration. It is formerly stated that a high ratio indicate an internal diffusion control; which is in good agreement with the obtained experimental data as in a high concentrated solution the internal diffusion provides a much higher resistance compared to external diffusion. However, this cannot exclude the effect of chemical reaction which, depending on its value, is the most pronouncing and is thus the controlling step in both solution concentrations. Therefore, the order of the experimentally obtained values of adsorption extent follows the ranking order of the
values in case of low concentrations are almost the same around unity with a slight variation while they differ appreciably in case of high concentration. It is formerly stated that a high ratio indicate an internal diffusion control; which is in good agreement with the obtained experimental data as in a high concentrated solution the internal diffusion provides a much higher resistance compared to external diffusion. However, this cannot exclude the effect of chemical reaction which, depending on its value, is the most pronouncing and is thus the controlling step in both solution concentrations. Therefore, the order of the experimentally obtained values of adsorption extent follows the ranking order of the  values.
values.
6. CONCLUSION
A mathematical model is proposed to simulate the adsorption of three metal ions (Zn2+, Cu2+, and Cd2+) from nitrate solutions using two different concentrations (10–2 and 10–4 M) with XAD2-HL impregnated resins. Adsorption is done via a counter-flow moving bed reactor. The model takes into consideration the internal and external diffusion effects as well as the effect of chemical reaction. The effect of these parameters beside other suggested ones on the adsorption extent has been investigated. The model allows the calculation of the required reactor height against the conversion extent. The process is found to be controlled by chemical reactions as a high solution velocity is utilized to simulate the operation conditions of industrial moving beds and to avoid the formation of a concentration gradient along the bed, either in the resin or in the solution. Thus, the solution composition remains practically constant throughout the experiment. Accordingly, the test conditions are directed towards the individual values of  that are much less than the corresponding values of
that are much less than the corresponding values of  or
or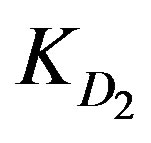 .
.
LIST OF SYMBOLS
Ac: Cross-sectional area of resin column (m2);
b: Number of active sites in a unit surface area (mole/m2);
Gs: Superficial mass velocity of resins (kg/(m2·s));
K1: Chemical reaction rate parameter (kg/(m2·s));
KD1: External diffusion parameter (s–1);
KD2: Internal diffusion parameter (s–1);
Kgr: Resin-specific reaction rate parameter (s–1);
L: Reactor height (m);
N: Number of moles adsorbed per particle per unit time (moles/s);
q: Adsorbed metal ion concentration per unit resin mass (mole/kg);
qe: Equilibrium concentration of adsorbed metal ions per unit resin mass (mole/kg);
rb: Radius of boundary layer (m);
rKD: Diffusion parameter ratio, dimensionless;
t: Time (s);
x: Fractional adsorption extent, dimensionless;
z: Fractional column height (vertical distance in m of reactor length starting from the solid entrance).
GREEK LETTERS
ΔKD: Diffusion parameter difference (s–1);
ρ: Resin density (kg/m3);
εs: Fractional holdup of resins in column, dimensionless;
n: Relative resin velocity factor (m/s).