1. Introduction
The objective of global optimization is to find the globally best solution of (possibly nonlinear) models, in the search space. Formally, global optimization seeks global solution of a constrained optimization model. Nonlinear models are ubiquitous in many applications, e.g., in advanced engineering design, data analysis, financial planning, scientific modeling, and others. These solutions often require a global search approach.
The field of swarm intelligence is an emerging research area that presents features of self-organization and cooperation principles among group members bio-inspired on social societies. Swarm Intelligence (SI) is the property of a system whereby the collective behaviours of agents interacting locally with their environment cause coherent functional global patterns to emerge.
Gravitational search algorithm (GSA), is a population based swarm optimization technique which was introduced by Rashedi et al. in 2009 [1], is a population based evolutionary optimization inspired by law of gravity. Similarly to genetic algorithms [2], GSA is an optimization tool based on a population, where each member is seen as a mass, and each mass is a potential solution to the problem under analysis. It has already been shown that GSA is comparable in performance with other evolutionary algorithms such as particle swarm optimization (PSO) [3] and Genetic Algorithm (GA) [2].
The basic idea of the GSA is to mimic the physical attraction between masses. Agents are considered as objects and their performance is measured by their masses. All these objects attract each other by the gravity force, and this force causes a global movement of all objects towards the objects with heavier masses.
At the end of the 19th century, classical mechanics encountered major difficulties in describing motions of microscopic particles with extremely light masses and extremely high velocities, and the physical phenomena related to such motions. These aspects forced scientists to rethink the applicability of classical mechanics and lead to fundamental changes in their traditional understanding of the nature of motions of microscopic objects [4]. The studies of Bohr, de Broglie, Schrödinger, Heisenberg and Bohn in 1920s inspire the conception of a new area, the quantum mechanics [5].
Recently, the concepts of quantum mechanics and physics have motivated the generation of optimization methods. Inspired by the GSA and quantum mechanics theories, this work presents a new Quantum-behaved GSA (QGSA) approach with outstanding result for unimodal functions.
The rest of the paper is organized as follows: Section 2 describes the features of classical GSA for continuous optimization, while Sections 3 explains the QGSA. Section 4 presents the results of the optimization. Lastly, some conclusion remarks are given in Section 5.
2. Classical Gravitational Search Algorithm
GSA is a global search strategy that can handle efficiently arbitrary optimization problems. Inspired by law of gravity, Rashedi et al. introduced the GSA method which is based on the Newtonian gravity. In the GSA, agents are considered as objects and their performance is measured by their masses. All these objects attract each other by the gravity force, and this force causes a global movement of all objects towards the objects with heavier masses.
The procedure for implementing the classical version of GSA is given by the following steps:
Step 1. Initialization of agent positions: Initialize a population (array) of agents with random positions in the D-dimensional problem space using uniform probability distribution function. To this aim, the GSA consider a system with  agents (masses), the position of the
agents (masses), the position of the  th agent is defined as follows:
th agent is defined as follows:
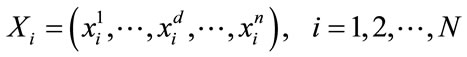 (1)
(1)
where  is the position of
is the position of  th mass in the
th mass in the  th dimension and
th dimension and  is dimension of the search space.
is dimension of the search space.
Step 2. Evaluation of agent’s fitness: Evaluate each agent’s fitness value.
Step 3. Update ,
,  ,
,  ,
,  for
for : In GSA, the gravitational constant,
: In GSA, the gravitational constant,  , will take an initial value,
, will take an initial value,  , and it will be reduced by time:
, and it will be reduced by time:
 (2)
(2)
Based on [1], the mass of each agent is calculated after computing current population’s fitness as follows:
 (3)
(3)
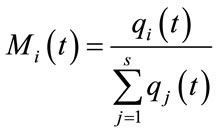 (4)
(4)
where  and
and represent the mass and the fitness value of the agent
represent the mass and the fitness value of the agent  at
at , and,
, and,  and
and  are defined as follows (for a maximization problem):
are defined as follows (for a maximization problem):
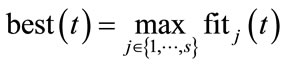 (5)
(5)
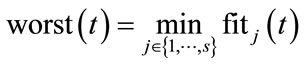 (6)
(6)
Step 4. Calculation of the total force in different directions: The total forces from a set of heavier masses that apply on agent 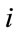 is calculated based on law of gravity as follow:
is calculated based on law of gravity as follow:
 (7)
(7)
where  is a uniform random in the interval
is a uniform random in the interval , ε is a small value, and
, ε is a small value, and  is the Euclidian distance between two agents
is the Euclidian distance between two agents 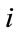 and
and  defined as
defined as .
.  is the set of first
is the set of first  agents with the best fitness value and biggest mass.
agents with the best fitness value and biggest mass.  is a function of time, initialized to
is a function of time, initialized to  at the beginning and decreasing with time. Here,
at the beginning and decreasing with time. Here,  is set to
is set to  (total number of agents) and is decreased linearly to 1.
(total number of agents) and is decreased linearly to 1.
Step 5. Calculation of acceleration and velocity: Agent acceleration is calculated by using law of motion as follow:
 (8)
(8)
where  is a uniform random in the interval
is a uniform random in the interval .
.
Then, the next velocity of an agent is calculated as a fraction of its current velocity added to its acceleration.
 (9)
(9)
Step 6. Updating agents’ position: Change the agent’s position,  , according to Equation (10).
, according to Equation (10).
 (10)
(10)
Step 7. Repeating the evolutionary cycle: Repeat steps 2 to 6 until the stop criteria is reached, usually a sufficiently good fitness or a maximum number of iterations (generations).
3. Quantum Formulation of the Agent Dynamics
As per classical mechanics, an individual is depicted by its position vector  and velocity vector
and velocity vector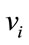 , which determine the trajectory of the individual. The individual moves along a determined trajectory in Newtonian mechanics, but this is not the case in quantum mechanics. In quantum world, the term trajectory is meaningless, because
, which determine the trajectory of the individual. The individual moves along a determined trajectory in Newtonian mechanics, but this is not the case in quantum mechanics. In quantum world, the term trajectory is meaningless, because 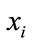 and
and  of an individual cannot be determined simultaneously according to uncertainty principle. Therefore, if individual agent in a GSA system has quantum behavior, the GSA algorithm is bound to work in a different fashion.
of an individual cannot be determined simultaneously according to uncertainty principle. Therefore, if individual agent in a GSA system has quantum behavior, the GSA algorithm is bound to work in a different fashion.
In quantum time-space framework, the quantum state of an individual is depicted by wave function 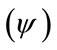 instead of position.
instead of position.  is the probability that measurement of the individual’s position finds it about the point whereby
is the probability that measurement of the individual’s position finds it about the point whereby .
.
In quantum mechanics, the governing equation is the general time-dependent Schrödinger equation,
 (11)
(11)
where 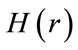 is a time-independent Hamiltonian operator given by,
is a time-independent Hamiltonian operator given by,
 (12)
(12)
where  is Planck’s constant,
is Planck’s constant, is the mass of the individual, and
is the mass of the individual, and  is the potential energy distribution. Its amplitude squared is the probability that measurement of the individual’s position at the time
is the potential energy distribution. Its amplitude squared is the probability that measurement of the individual’s position at the time  finds it in the volume element about the desired point. By imposing the following normalization condition we can justify such a measure,
finds it in the volume element about the desired point. By imposing the following normalization condition we can justify such a measure,
 (13)
(13)
Now, we hypothesize that the GSA system is a quantum system, each mass of which is of quantum state formulated by wave function. Inspired by analysis of convergence of the classical GSA in [1], we assume that an individual mass moves in a Delta potential well in feasible search space, of which the center is weighted average of all kbest. For simplicity, we consider an agent in one-dimensional space, the potential energy of the mass in one-dimensional Delta potential well is represented as:
 (14)
(14)
where  is a positive number proportional to the “depth” of the potential well. The depth is infinite at the origin and zero elsewhere.
is a positive number proportional to the “depth” of the potential well. The depth is infinite at the origin and zero elsewhere.
The Schrodinger equation for the model is,
 (15)
(15)
For  the equation can be written as,
the equation can be written as,
 (16)
(16)
In order to prevent diverging of agents the following boundary conditions is applied
 (17)
(17)
To satisfy the bound condition, Equation (16) is calculated as follow:
 (18)
(18)
QGSA is the integration of quantum computing and GSA. The QGSA is based on the representation of the quantum state vector.
To evaluate the fitness value, we need to learn of precise information of position of the agent. However, the quantum wave function can only give the probability density function that the mass appears at the desired position. So we have to gauge the position of the individual, which is called collapsing the quantum state to the classical state. According to Monte Carlo Method of uncertainty, it is possible to simulate the process of measurement. The procedure of simulation is described as follows.
To this aim, a random variable 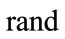 is generated uniformly distributed between 0 and 1, so Equation (18) can be simplified with substituting a random number instead of it,
is generated uniformly distributed between 0 and 1, so Equation (18) can be simplified with substituting a random number instead of it,
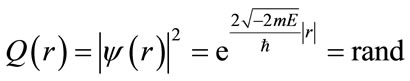 (19)
(19)
where  is a random number uniformly distributed on
is a random number uniformly distributed on .
.
 (20)
(20)
Thus, the position of agent accurately is measured as follows,
 (21)
(21)
where  is the only parameter of the algorithm.
is the only parameter of the algorithm.
The procedure for implementing the QGSA is given by the following steps:
Step 1. Initialization of mass positions: Initialize a population (array) of masses with random positions in the D-dimensional problem space using a uniform probability distribution function.
Step 2. Evaluation of particle’s fitness: Evaluate the fitness value of each agent.
Step 3. Selecting  and update
and update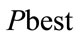 :
:  is the set of first
is the set of first  agents with the best fitness value and biggest mass. In order to updating
agents with the best fitness value and biggest mass. In order to updating , compare each agent’s fitness with the agent’s
, compare each agent’s fitness with the agent’s . If the current value is better than
. If the current value is better than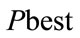 , then set the
, then set the  value equal to the current value and the
value equal to the current value and the  location equal to the current location in D-dimensional space.
location equal to the current location in D-dimensional space.
Step 4: Updating the  using Equation (23):
using Equation (23):
 (22)
(22)
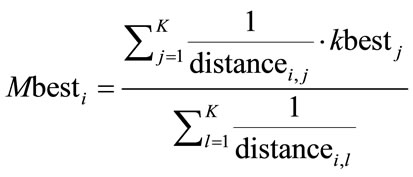 (23)
(23)
Step 5. Updating of masses’ position: Change the position of the mass where  and
and  are two random numbers generated using a uniform probability distribution in the range
are two random numbers generated using a uniform probability distribution in the range .
.
 (24)
(24)
Employing the Monte Carlo method, the masses move according to the following iterative equation:
 (25)
(25)
where  is a design parameter called contraction-expansion coefficient,
is a design parameter called contraction-expansion coefficient,  and
and  are values generated according to a uniform probability distribution in range
are values generated according to a uniform probability distribution in range .
.
Step 6. Repeating the evolutionary cycle: Loop to Step 2 until a stop criterion is met, usually a sufficiently good fitness or a maximum number of iterations (generations).
4. Numerical Results
In this study, to evaluate the performance of the QGSA, 7 minimization benchmark functions [1,4] listed in Table 1 are used for comparison with classical GSA. In Table 1,  is the dimension of search space (function),
is the dimension of search space (function), 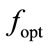 is the minimum value of the function. The minimum value (
is the minimum value of the function. The minimum value ( ) of the functions of Table 1 are zero. The test functions are unimodal high-dimensional functions which make them suitable for evaluating performance of the algorithm in point of view convergence rate.
) of the functions of Table 1 are zero. The test functions are unimodal high-dimensional functions which make them suitable for evaluating performance of the algorithm in point of view convergence rate.
We evaluate the unimodal optimization algorithm in two aspects: quality, and precision of solutions.
Quantity: Number of needed fitness function evaluations to reach the global optimum. It means the convergence rate of search algorithm.
Precision or accuracy: The difference between the global minimum and one but lowest minimum determines the possibility to detect the global minimum point.

Table 1. Benchmark functions used in this study.
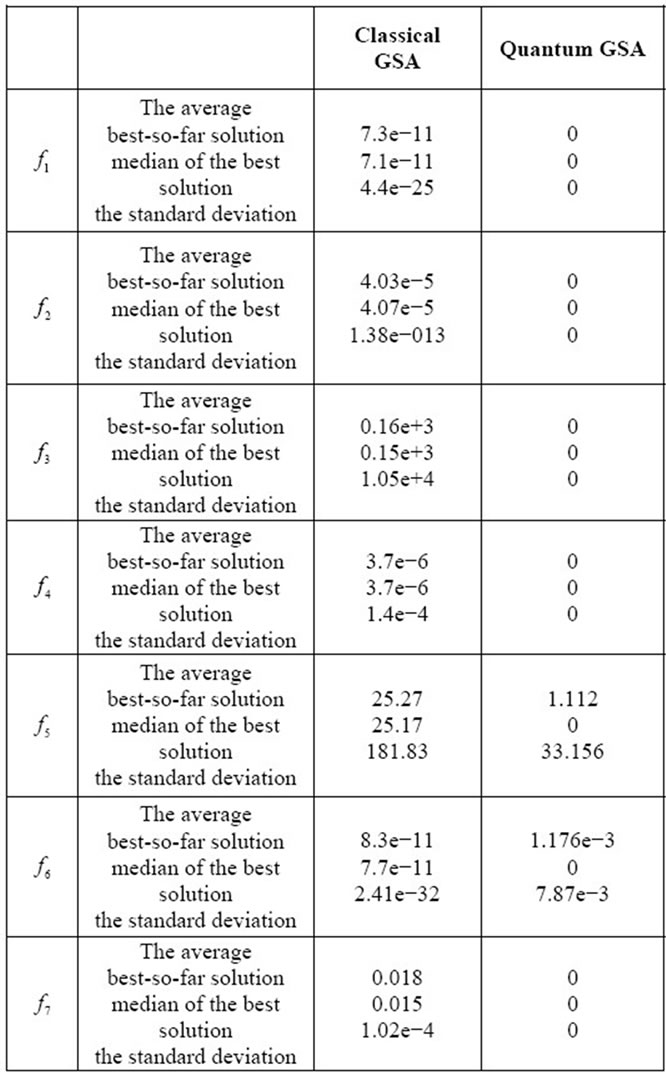
Table 2. Minimization result of functions in table 1. Results are averaged over 30 runs and the average best-so-far and standard deviation of best solution obtained at last iteration are given.
In unimodal functions, the convergence rate of search algorithm is more important than the final results because there are other methods which are specifically designed to optimize unimodal functions.
The results are averaged over 30 runs and the average best-so-far solution, median of the best solution and the standard deviation in the last iteration are reported for unimodal functions in Table 2. As this table illustrates QGSA provides better results than GSA for all functions. In these function QGSA tends to find the global optimum faster than classical GSA and hence has a higher convergence rate.
The numerical results in Table 2 show that almost the QGSA could hit the optimal solution with high precision.
There are two exception test functions which QGSA cannot tune itself and have not a good performance.
In Rosenbrock function, the global optimum is inside a long, narrow, parabolic shaped flat valley. To find the valley is trivial, so converging to the global minimum, however, is difficult. Hence QGSA could not tune itself.
Also, the good convergence rate of QGSA could be concluded from Figures 1 to 7. According to these figures, QGSA tends to find the global optimum in an acceptable time hence has a high convergence rate.

Figure 1. Comparison of performance of QGSA and GSA for minimization of .
.

Figure 2. Comparison of performance of QGSA and GSA for minimization of .
.

Figure 3. Comparison of performance of QGSA and GSA for minimization of .
.
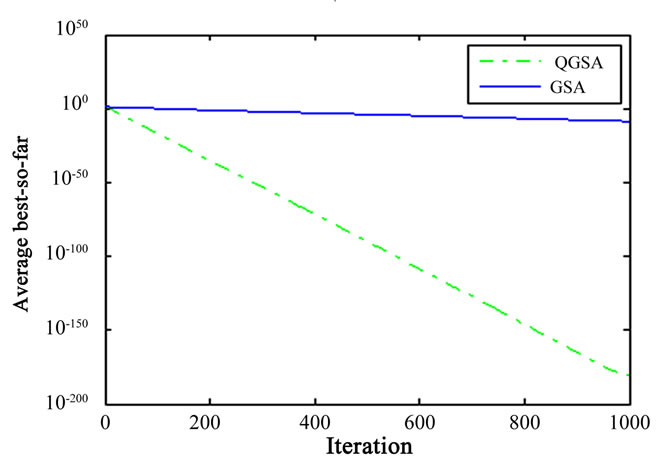
Figure 4. Comparison of performance of QGSA and GSA for minimization of .
.

Figure 5. Comparison of performance of QGSA and GSA for minimization of .
.
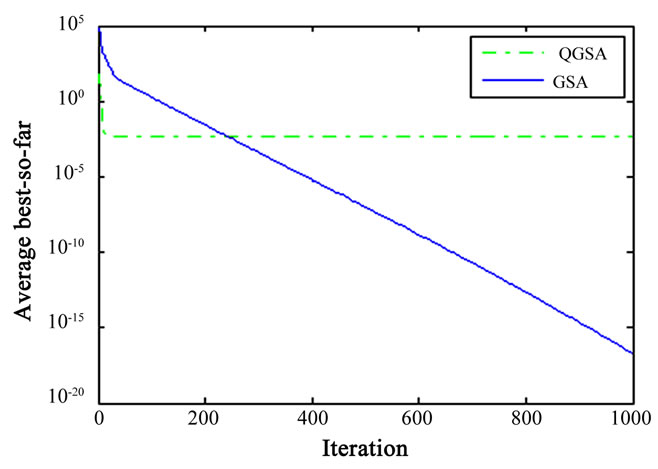
Figure 6. Comparison of performance of QGSA and GSA for minimization of .
.
The reported results for dimension 30 by for different test functions are summarized in Table 2. According to Figures 1 to 7, we can see that QGSA provides better solutions except for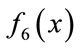 .
.

Figure 7. Comparison of performance of QGSA and GSA for minimization of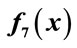 .
.
5. Conclusion
In this paper, a quantum version of gravitational search algorithm is introduced called as QGSA. It is tasted on different benchmark functions to investigate the efficiency of QGSA. The results show that QGSA is performing much better than GSA in finding the optimum result. Although the used functions are unimodal functions but it could expand it to multimodal functions. Currently, the authors are working on the improvement of the proposed QGSA.