We propose a double forecasting model using stochastic theory .The demand of automobile loan is the sum of all compound variables which indicated that automobile loan was credited to customer occurring in a certain period of time. Probability distribution of automobile loan was acquired using throughout probability theory. In view of such a fact, demand of automobile loan can be viewed as a conditional mathematic expectation. The forecasting model is proposed using growing function. Theoretical analysis and Case study shows that model based on conditional expectation is better than other model available with respect to forecasting demand of automobile loan.
1. Introduction
In China, the rapid increase in the demand for private cars is an important and sensitive issue. On the one hand, there is the expressed intention of the Chinese government to use the car industry as an engine to promote industrial and economic growth. Forecasting consumer demand for automobile loan is becoming ever more difficult as consumer preferences change rapidly and the market environment becomes more complex. Nevertheless, the importance of forecasting future demand cannot be overemphasized for the purposes of both investment decisions and policymaking. Besides, it has been becoming significant and difficult subject to construct a model of demand of automobile loan to describe the developing trends of automobile loan.
John K. Dagsvik and Gang Liu developed a general random utility framework for analyzing data on individuals’ rank-orderings. They show that in the case with three alternatives one can express the probability of a particular rank-ordering as a simple function of first choice probabilities. Their framework is applied to specify and estimate models of household demand for conventional gasoline cars and alternative fuel vehicles in Shanghai based on rank-ordered data obtained from a stated preference survey [1]. Jongsu Lee and Youngsang Cho predicted consumer demand for diesel passenger cars. The model accommodates governmental policies and car attributes such as price and engine efficiency. They noted that consumers will likely prefer diesel passenger cars to gasoline ones due to the low operation costs of the former in spite of high purchase price when diesel is relatively cheaper than gasoline [2]. Astrid A. Dick proposed a method to estimate a structural demand model for commercial bank deposit services in order to measure the effects on consumers given dramatic changes in bank services throughout US branching deregulation in the 1990s [3]. Wouter J. den Haan et al. investigated the portfolio behavior of bank loans following a monetary tightening and noted that real estate and consumer loans sharply decrease, while commercial and industrial (C&I) loans increase. They presented some arguments why the supply of C&I loans may actually increase after a monetary contraction [4]. Li-Chiu Chi studied the impact of a borrower’s reorganization filing on its lead lending bank and second lending bank. He proposed an innovative application by providing an empirical exposition of the receiver operating characteristic curve analysis and by presenting the results of the model’s performance in reliability and robustness [5].
Wang Qin described the transformation of the consumer durable goods of Chinese citizens in the past fifty years and calculated the future demand on China’s car consumption markets. Meanwhile, he analyzed the status of China’s consumer car loans. He draws a conclusion that the potential car market of China was very big and the prospect of China’s consumer car loan is immensurable [6]. Ye Qian utilized GM(1,1) model to predict and analyze the changes of credit in China in recent years. He proposed four schemes to give solutions to problems such as the data deficiencies that results in information excavating distortion and the “noises” included in the data processing [7].
Two major methods are used to forecast the demand for automobile loan, namely, random utility theory and GM(1,1).Random utility theory focused on the estimation of consumer preferences for the product attributes separately using discrete choice models, and GM(1,1) is a kind of grey prediction model that extracts valuable information through producing and exploring “some” known information.
Research on demand forecasting for automobile loan has been ongoing in many countries because of the importance of the financial industry. There exists a substantial body of research on demand forecasting for automobile loan using random utility theory and demand forecast based on random utility theory and GM(1,1) is difficult to dealt with more complex situations. For example, random utility theory is difficult to predict exact value of demand of automobile loan, meanwhile, GM(1,1) can predict value of demand of automobile loan but it is difficult to cope with some situations depend on social and economic policy.
This paper makes two contributions. The main contribution is to establish a model for demand of automobile loan based on conditional expectation. This implies that a model for demand of automobile loan based on conditional expectation is better than other model available. Second, we apply this model to analyze demand for automobile loan in a bank of Shandong province.
2. Establishment of a Forecasting Model for Automobile Loan
2.1. Problem Statement
m currency unit were credited to customer who apply for automobile for a period of time, number of automobile loan was approved by bank is N. It is a part of stochastic progress {N(t), t ≥ 0}. XN currency unit was handled N(t) times at a certain time t. It is assumed that automobile loan will finish n currency unit. Our aim is to acquire the future demand of automobile loan.
2.2. Basic Notions
Lemma 2.2.1 If X,Y are random variable, then E[E(X|Y)] = E(X)
Lemma 2.2.2 Let SN = X1 + X2 + …. + XN. N is a uncertain positive integer. {Xk} is a sequence of independent identical distribution. We get

2.2.3 Definition of growing function

2.2.4 Conditional mathematical expectation of X On the assumption that f(x,y) is is a combine consistency function of (X,Y),We get


Thus,

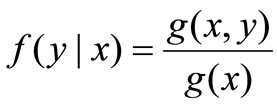
Conditional mathematical expectation of Y when X=x is as follows:

Similarity,

Theorem 1 Let , C is a random variable and constant, respectively. Then
, C is a random variable and constant, respectively. Then  hold.
hold.
2.3. Establishment of the Model
The demand of automobile loan is as follows:
 where,
where,  is a stochastic process, and
is a stochastic process, and are independent and identically distributed random variables, with distribution function G, which are also independent of
are independent and identically distributed random variables, with distribution function G, which are also independent of . Some notation used in the model is defined:
. Some notation used in the model is defined:
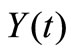 demand of automobile loan occurring in a certain time interval [0,t]
demand of automobile loan occurring in a certain time interval [0,t]
N(t) It is a part of stochastic progress {N(t), t ≥ 0},which indicate that the times of automobile loan was credited to customer occurring in a certain time interval [0,t]
 It indicates that
It indicates that  currency unit was credited to customer occurring in a certain time interval [0,t]
currency unit was credited to customer occurring in a certain time interval [0,t]
We can acquire distribution function of demanding of automobile loan using Formula of Total Probability:
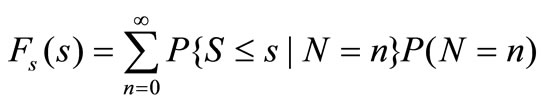



At the same time, Distribution law of demanding of automobile loan is as follows:

The definition of  is similar to
is similar to .
.
Obviously,

where  denotes that automobile loan has been credited to applicants,
denotes that automobile loan has been credited to applicants, 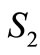 denotes that automobile loan will credited to applicants.
denotes that automobile loan will credited to applicants.
The demand of automobile loan is as follows:

Thus,

The series of automobile loan is as follows:

where  denotes automobile loan in i+1-th year,
denotes automobile loan in i+1-th year,  denotes automobile loan i-th year.
denotes automobile loan i-th year.
3. Numeric Results
The data set consists of 16,237 applications for an automobile loan at a major bank of Shandong province between September 2002 and August 2009.
In a certain short time interval, the Distribution law of applicants and their total volume per time are shown in Tables 1 and 2.
Thus, distribution law of automobile loan is acquired using Convolution (Table 3).
The total time is devided into some short time interval i. Let Si indicate the volume in time interval i, thus is the Convolution of Si.
Automobile loan in 2006 is as follows:

Table 1. The distribution law of applicants.

Table 2. The distribution law of volume of applicants per time (unit: Ten thousand Yuan).

Table 3. The distribution law of automobile loan in this time interval.

Table 4. The comparison of the root mean PRESS.

Actual results in 2006 is 100,900 millions Yuan, relative error is 0.6%.
Aiming to further testify the efficiency of the model, we selected automobile loan in the bank from 2004 to 2006 to test using different models. The results are shown in Table 4.
Table 4 shows that model based on conditional mathematic expectation is an efficient one with respect to forecasting demanding of automobile loan.
4. Conclusions
In this paper we have argued two related points. The first is that model based on conditional mathematic expectation is an efficient approach for forecasting demand of automobile loan than other model available. The second is that automobile loan doesn’t increase forever. A more general implication of our finding for demanding for automobile loan is perhaps that it supports the present shift in many countries from monetary targeting to credit targeting with the loan rate as an effective tool of credit control. Banks may also be forecasting survival time, or loss rates, or both using model proposed in this paper.
[1] J. K. Dagsvik and G. Liu, “A Framework for Analyzing Rank-Ordered Data with Application to Automobile Demand,” Transportation Research Part A: Policy and Practice, Vol. 43, No. 1, 2009, pp. 1-12.
[2] J. Lee and Y. Cho, “Demand Forecasting of Diesel Passenger Car Considering Consumer Preference and Government Regulation in South Korea,” Transportation Research Part A: Policy and Practice, Vol. 43, No. 4, 2009, pp. 420-429.
[3] A. A. Dick, “Demand Estimation and Consumer Welfare in the Banking Industry,” Journal of Banking & Finance, Vol. 32, No. 8, 2008, pp. 1661-1676.
[4] W. J. den Haan, S. W. Sumner and G. M. Yamashiro, “Bank Loan Portfolios and the Monetary Transmission Mechanism,” Journal of Monetary Economics, Vol. 54, No. 3, 2007, pp. 904-924.
[5] L.-C. Chi, “How have Banks Fared Following a Borrower’s Financial Distress,” Economic Modelling, Vol. 26, No. 2, 2009, pp. 480-488.
[6] Q. Wang, “Forecast and Analysis on the Prospect of China’s Consumer Car Loan,” Operations Research and Management Science, Vol. 11, No. 2, 2002, pp. 117-121.
[7] Q. Ye, “Improving on GM (1,1) and its Application in the Forecast of Bank Loan,” Mathematics in Practice and Theory, Vol. 38, No. 18, 2008, pp. 20-27.