Sinc-Collocation Method for Solving Linear and Nonlinear System of Second-Order Boundary Value Problems ()
1. Introduction
Numerous problems in physics, chemistry, biology and engineering science are modelled mathematically by systems of ordinary differential equations, e.g. series circuits, mechanical systems with several springs attached in series lead to a system of differential equations (for example see [1,2]). However, many classical numerical methods used with second-order initial value problems cannot be applied to second-order boundary value problems (BVPs).
Most realistic systems of ordinary differential equations do not have exact analytic solutions, so approximation and numerical techniques must be used. There are many publications dealing with the linear system of second-order boundary value problems. They introduced various numerical methods. For instance, a finite difference method has been proposed in recent works [3-8]. For a nonlinear system of secondorder BVPs, there are few valid methods to obtain numerical solutions. Geng et al. have studied the numerical solution of a nonlinear system of second-order boundary value problems in the reproducing kernel space [9]. Lu considered the variational iteration method to solve a nonlinear system of second-order boundary value problems [10]. Recently, Bataineh et al. [11] represented modified homotopy method for solving systems of second-order boundary value problems. Sinc-collocation method was applied to solve nonlinear systems of second order boundary value problems in [12].
In this paper, we discuss the use of sinc-collocation method for solving a class of linear and non-linear system of differential equations
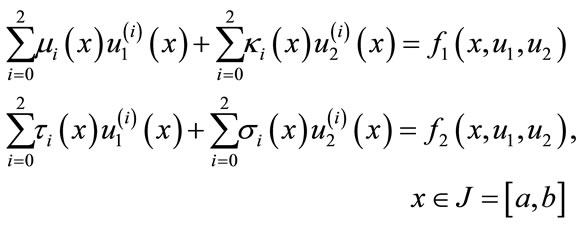(1)
subject the boundary conditions
(2)
where
, 
, 
, 
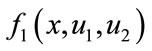, and
, 
, 
, and
, for
, are analytic functions. It will always be assumed that (1) possesses a unique solution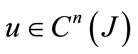
.
Numerical examples including regular, singular as well as singularly perturbed problems are considered. On the basis of these examples, the results reveal that the method is very effective and convenient.
The paper is organized into five sections. Section 2 contains notation, definitions and some results of sinc function theory. In Section 3, the sinc-collocation method is developed for linear second-order system of differential equation with homogeneous boundary conditions. The method is developed for nonlinear second-order system of differential equation in Section 4. Some numerical examples are presented in Section 5. Finally, Section 6 provides conclusions of the study.
2. Sinc Function
In recent years, a lot of attention has been devoted to the study of the sinc method to investigate various scientific models. The efficiency of the method has been formally proved by many researchers [13-22].
A general review of sinc function approximation is given in [23,24]. Hence, only properties of the sinc function that are used in the sequel.
If 
is defined on the real line, then for 
the Whittaker cardinal expansion of f is given by:
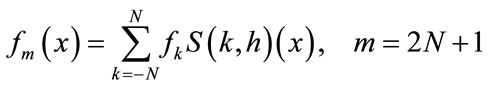(3)
where
, 
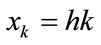, and the mesh size is given by
(4)
where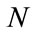 
is suitably chosen and 
depends on the asymptotic behavior of
. The n-th derivative of the function f at the sampling points 
can be approximated using a finite number of terms as:
where
In particular,
(5)
(6)
and
(7)
We note that
The interpolation formula fo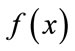r 
over 
takes the form
(8)
where the basis functions on 
are then given by
and the transformation function
(9)
transforms 
to the infinite range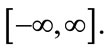 
The interpolation points 
are then given by:
The n-th derivative of the function 
at points 
can be approximated using a finite number of terms as
(10)
Setting
and noting that
and
which will be used later.
3. System of Linear Second Order Equations
Consider a linear, system of linear second order equations of the form
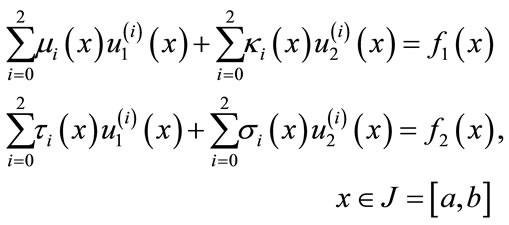(11)
We assume that 
and 
the solutions of (11) and (2), is approximated by the finite expansion of Sinc basis functions
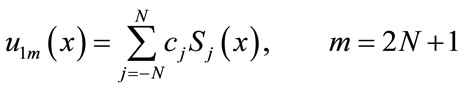(12)
and
(13)
where 
is the function 
for some fixed step size h. If we replace each term of (11) with its corresponding approximation given by the right-hand side of (10) and (8) we have
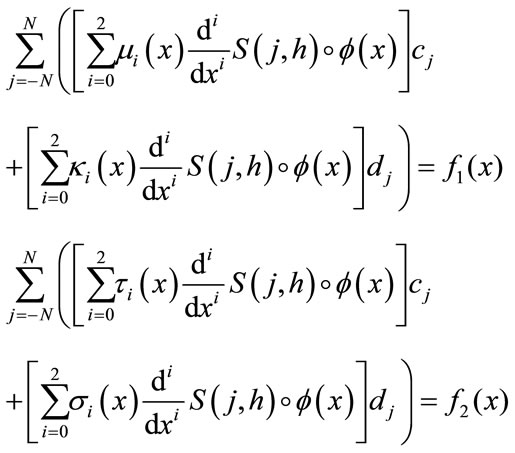(14)
Substituting 
in (14) and applying the collocation to it, we eventually obtain the following theorem.
Theorem: If the assumed approximate solution of problem (11) and (2) is (12) and (13) , then the discrete sinc-collocation system for the determination of the unknown coefficients is given by
(15)
where
and
Now, since
, 
and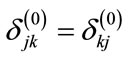
, we write the above equation in the form
(16)
We now rewrite these equations in matrix form. The system in (16) takes the matrix form
(17)
where
Now we have a linear system of 
equations of the 
unknown coefficients. We can obtain the coefficients of the approximate solution by solving this linear system. The system (17) may be easily solved by a variety of methods. In this paper we used the Q-R method. The solution c gives the coefficients in the approximate sinc-collocation solutions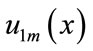 
and 
of 
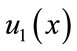and
.
4. System of Non-Linear Second Order Equations
Consider a nonlinear, system second-order equations of the form
(18)
where 
and 
are nonlinear functions of 
and 
is an analytic function and 
may be a polynomial or a rational function, or exponential. Due to the large number of different possibilities, our work will be focused mainly on the following forms 
1) 
2) 
3) 
or any analytic function of 
which has a power series expansion. We limit our study to the case
where 
is an integer, or a fraction.
We consider next applying of the sinc-collocation method to solve problem (18) and (2).
Lemma: The following relation holds
(19)
where N and h are now dependent on both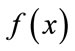 
and
.
Replacing the terms of (18) with the appropriate representation defined in (8), (10) and (19) and applying the collocation to it, we eventually obtain the following theorem.
Theorem: If the assumed approximate solution of problem (18) and (2) is (12) and (13), then the discrete sinc-collocation system for the determination of the unknown coefficients is given by
(20)
Let 
be the 
-vector with j-th component given by
. In this notation the system in (20) takes the matrix form
(21)
where
Now we have a nonlinear system of 
equations in the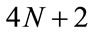 
unknown coefficients. We can obtain the coefficients in the approximate solution by solving this nonlinear system by Newton’s method.
Starting from an initial estimate
, the corrections are made using
Here, 
is the current iterate, and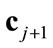 
is the new iterate. A common numerical practice is to stop the Newton iteration whenever the distance between two iterates is less than a given tolerance, i.e. when
where the Euclidean norm is used. The solution 
gives the coefficients in the approximate sinc-collocation solution 
of
.
5. Numerical Examples
In this section, some numerical examples are studied to demonstrate the accuracy of the present method. The results obtained by the method are compared with the exact solution of each example and are found to be in good agreement with each other.Comparison between sinc-collocation and other method shall be presented.
All computations were carried out using Matlab on a personal computer with a machine precision of
. In all cases, 
is taken to be
. The selection of a larger 
yields more accuracy, but at the expense of a lengthier computation. We report absolute error which is defined as
Example 1: [3,11] consider the linear system of second order boundary value problems
where
subject to the boundary conditions
whose exact solutions are
Maximum absolute errors for 
and 
are tabulated in Table 1 for the sinc-collocation method.
Maximum absolute error are tabulated in Table 2 for sinc-collocation together with the analogous results of N. Caglar and H. Caglar [3].
Example 2: [11] Now we turn to a nonlinear problem
where
subject to the boundary conditions
whose exact solutions are
The computational results are summarized in Table 3.
Example 3: Now we turn to a singular problem,
where
subject to the boundary conditions
whose exact solutions are
Table 1. Maximum absolute error for example 1.
Table 2. Comparison between maximum absolute error for example 1.
Table 3. Maximum absolute error for example 2.
The computational results are summarized in Table 4.
Example 4: Another example is also a singular problem
where
subject to the boundary conditions
whose exact solutions are
Maximum absolute errors for 
and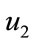 
are tabulated in Table 5 for the sinc-collocation method.
Example 5: Our final example is the singularly perturbed problem
Table 4. Maximum absolute error for example 3.
Table 5. Maximum absolute error for example 4.
where
subject to the boundary conditions
whose exact solutions are
Table 6 the maximum absolute errors obtained by using the sinc-collocation method for N = 40 and different
.
6. Conclusions
This paper described an efficient method for solving the system of second-order boundary value problems. Our approach was based on the sinc-collocation method. Properties of the sinc-collocation method are utilized to reduce the computation of this problem to some linear or nonlinear algebraic equations. The method is computationally attractive and applications are demonstrated through illustrative examples. Numerical examples including regular, singular as well as singularly perturbed problems are presented. As expected, the accuracy increases as the number of terms N in the sinc expansion increases. The obtained results showed that this approach can solve the problem effectively.
The sinc-collocation method is a simple method with high accuracy for solving a large variety of linear and nonlinear system of differential equations. So it may be
Table 6. Maximum absolute error for example 5.
easily applied by researchers and engineers familiar with the sinc function. Extension of the method for solving systems of partial differential equations offers an excellent opportunity for future research.