Necessary Conditions for a Fixed Point of Maps in Non-Metric Spaces ()
1. Introduction
Let X denote a complete (or compact) metric space and also  a continuous map of X onto Y, where Y is a bounded closed topological normal space with a countable base.
a continuous map of X onto Y, where Y is a bounded closed topological normal space with a countable base.
What must be the conditions, in the means of the meric space X, such that the continuous map  from Y onto Y will have a fixed point?
from Y onto Y will have a fixed point?
We suppose that (see [1-3]):
the continuous map  (not one to one) and the continuous map
(not one to one) and the continuous map 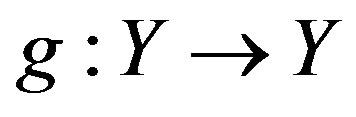 are given and the continuous inverse map of f,
are given and the continuous inverse map of f,  exists.
exists.

We remind that Banach contraction principle for multivalued maps is valid and also the next Theorem, proved by H. Covitz and S. B. Nadler Jr. (see [4]).
Theorem 1. Let 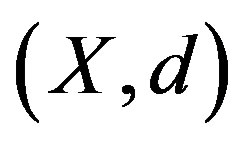 be a complete metric space and
be a complete metric space and  a conraction map (
a conraction map (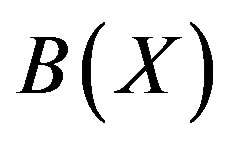 denotes the family of all nonempty closed bounded (compact) subsets of X). Then there exists
denotes the family of all nonempty closed bounded (compact) subsets of X). Then there exists  such that
such that .
.
2. Main Result
We consider now the next theorem:
Theorem 2. Let  denote a complete (or compact) metric space
denote a complete (or compact) metric space  and also:
and also:
 a continuous map of
a continuous map of  onto
onto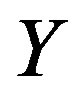 , where
, where  is a bounded closed topological normal space with a countable base.
is a bounded closed topological normal space with a countable base.
We suppose also that the maps:
 is continuous and onto.
is continuous and onto.
and
 exists and it is continuous.
exists and it is continuous.
If  is a point from
is a point from  and if we suppose also that
and if we suppose also that .
.
Then if the rest terms of the sequence  are received from
are received from  and the rest of the terms of the sequence
and the rest of the terms of the sequence 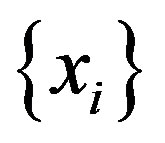 are determined by
are determined by 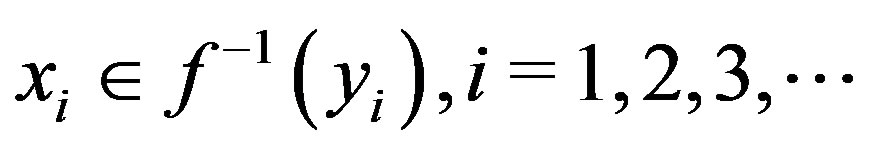 and if also
and if also  is a Cauchy sequence and therefore convergent to a fixed point
is a Cauchy sequence and therefore convergent to a fixed point  in
in , then the sequence
, then the sequence 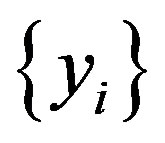 will be also convergent to a fixed point
will be also convergent to a fixed point  in
in .
.
Proof. Let  is a point from
is a point from 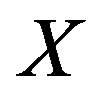 and let us suppose also that
and let us suppose also that 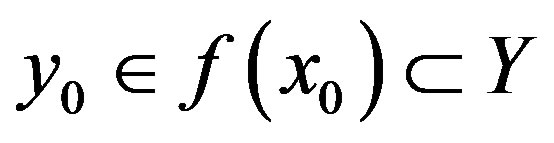 and let the rest terms of the sequence
and let the rest terms of the sequence 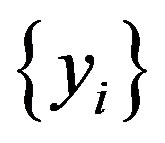 are received from
are received from 
 .
.
Let also the rest of the terms of the sequence  are determined by
are determined by 
 .
.
If  is a Cauchy sequence then for any
is a Cauchy sequence then for any  there exists an integer
there exists an integer , such that for all integers i and k,
, such that for all integers i and k, 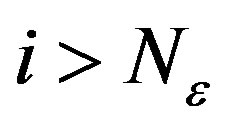 and
and  will be satisfied the inequality
will be satisfied the inequality

and therefore the Cauchy sequence  will be convergent with a fixed point
will be convergent with a fixed point 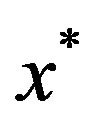 in X, and because X is complete (or compact), i.e.
in X, and because X is complete (or compact), i.e.

Since  and
and  and
and  is a continuous map and
is a continuous map and  is continuous map onto the closed and bounded space
is continuous map onto the closed and bounded space , and also
, and also 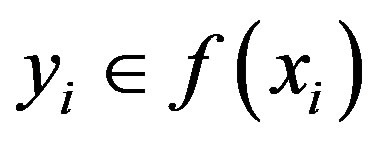 and
and , therefore the sequence
, therefore the sequence  will be also convergent with a fixed point
will be also convergent with a fixed point  in
in , such that
, such that  and
and , i.e.
, i.e.

Q.E.D.
3. Acknowledgements
We express our gratitude to Professor Alexander Arhangelskii from OU-Athens for creating the problem and to Professor Jonathan Poritz and Professor Frank Zizza from CSU-Pueblo for the precious help for solving this problem, and to Professor Darren Funk-Neubauer and Professor Bruce Lundberg for correcting some grammatical and spelling errors.