Performance Comparison of Electromagnetism-Like Algorithms for Global Optimization ()
1. Introduction
This paper studied the performance of a new class of evolutionary algorithms called electromagnetism-like (EML) algorithm, recently proposed by Birbil and Fang [1], for optimization problems with bounded variables in the form of:
 (1)
(1)
where f(x) is the objective function to be minimized,  is the variable vector, and L = (l1, l2, ···, ln) and U = (u1, u2, ···, un) are the lower bound and upper bound of x, respectively. That is, li ≤ xi ≤ ui for i = 1 to n.
is the variable vector, and L = (l1, l2, ···, ln) and U = (u1, u2, ···, un) are the lower bound and upper bound of x, respectively. That is, li ≤ xi ≤ ui for i = 1 to n.
EML algorithm simulates the interaction caused by electromagnetic force between electrically charged particles. Due to its effectiveness, EML algorithm has been applied to various optimization problems, such as scheduling [2-4], vehicle routing problems [5], feature selection [6], fuzzy neural system [7], and engineering design problems [8] since its inception.
The general scheme of an ELM algorithm [1] is shown in Figure 1. It consists of four phases: initialize a population of particles (step 1 in Figure 1), local search to exploit local optimums (step 3 in Figure 1), calculate the force exerted on each particle (step 4 in Figure 1), and move each particle along the direction of the force (step 5 in Figure 1).
Because of the simplicity of the EML scheme, many EML or EML-hybrid algorithms have been proposed in the literature. These algorithms mainly differ in the last three phases of the above general EML scheme. That is, different local search method can be used, and the force exerted on each particle and the new position of each particle can be calculated differently in different EML algorithms. Many of these EML algorithms have persuasive experimental results showing their superior performance over the original EML algorithm of Birbil and Fang [1]. However, due to the lack of comparison among these algorithms, the best way to design an EML algorithm remains unclear. Further, most of the experimental results are for optimization problems in a lower dimensional space, and it is unclear whether these EML algorithms scale well with high dimensionality. Birbil et al. [9] pointed out the premature convergence problem of the original EML algorithm, however, it also remains unclear whether these new EML algorithms can escape from local optimums effectively and efficiently.
The objectives of this study are threefold. Firstly, it surveys the literature for the alternatives for force calculation in the EML algorithms. Secondly, it uses an artifi-
cial problem instance together with non-uniformly distributed particles to provide a sanity check of these EML algorithms on their ability to escape from local optimums. Thirdly, it compares the performance of these EML algorithms using a set of well-known benchmark functions, ranging from low to high dimensionality. The results not only provide better understanding of these EML algorithms, but also guide the development of new EML algorithms.
2. Survey of EML Algorithms
This section reviews various local search methods (step 3 in Figure 1), force calculation methods (step 4 in Figure 1) and particle moving methods (step 5 in Figure 1) that have been adopted in the EML algorithms in the literature.
2.1. Local Search Methods
The purpose of local search is to move a particle to its nearby local optimums. Birbil and Fang [1] indicated that local search can be either omitted or applied to all particles or only the current best particle in the population. Omitting local search, an EML algorithm relies solely on the EML heuristics to find the optimal solution. However, applying local search to all particles is time consuming and offers slight improvement over applying local search only to the current best particle [1]. Therefore, in this study, local search is either omitted or applied only to the current best particle.
Various local search methods have been used in EML algorithms. Theoretically, any local search method can be adopted in ELM algorithms. Complex local search methods (e.g. chaos optimization [10] and pattern search [11]) help converge to and escape from local optimums. The original EML algorithm [1] uses a simple local search, called random line search, so that the benefit of the electromagnetism heuristics can be better appreciated. Therefore, random line search is also adopted in this study to allow fair comparison among various implementations of the electromagnetic heuristics in ELM algorithms.
Random line search requires two parameters: δ and LsIter. First, the maximum feasible step length rk at each dimension k is calculated as the product of δ and the range of dimension k (i.e. uk − lk). Then, for each particle i, this method searches along each dimension k for improvement of particle i for no more than LsIter times, as shown in Figure 2. Notably, this local search method is simple but has weak capability of escaping from local optimums.
2.2. Calculate Force and Move Particles
Various EML algorithms employ the electromagnetic

Figure 2. Random line search (for particle i at xi).
heuristics somewhat differently. For example, to move a particle, some algorithms consider the force exerting from all other particles to this particle, while some algorithms only consider the force exerting from an another particle. Furthermore, in some EML algorithms, the magnitude of the force between two particles is not inversely proportional to the square of their distance. The rest of this section surveys how the electromagnetism heuristics are interpreted in various EML algorithms.
2.2.1. Original Method
The original EML algorithm of Birbil and Fang [1] uses an electromagnetism-like attraction-repulsion mechanism to move particles as follows.
First, calculate the charge qi of each particle i using Equation (2):
 (2)
(2)
where xbest denotes the particle with the best objective value in current population (i.e. xbest = argmin{f(x),  i}), m is the number of particles, and n is the number of dimensions. All particles have charge between 0 and 1, and particles with better objective values have higher charges.
i}), m is the number of particles, and n is the number of dimensions. All particles have charge between 0 and 1, and particles with better objective values have higher charges.
Then, the force  exerted on particle i from another particle j is calculated using Equation (3):
exerted on particle i from another particle j is calculated using Equation (3):
 (3)
(3)
where  denote the distance between
denote the distance between  and
and . Notably,
. Notably,  and
and 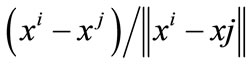 in Equation (3) are unit vectors, and thus the force
in Equation (3) are unit vectors, and thus the force  is inversely proportional to
is inversely proportional to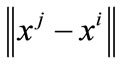 , which contradicts the electromagnetic heuristics that the force between two particles should be inversely proportional to the square of their distance. The total force
, which contradicts the electromagnetic heuristics that the force between two particles should be inversely proportional to the square of their distance. The total force  exerted on particle i from all other particles in the population is calculated using Equation (4):
exerted on particle i from all other particles in the population is calculated using Equation (4):
 (4)
(4)
Finally, all particles except xbest are moved using Equation (5):
 (5)
(5)
where k = 1, ···, n, and λ is a random value uniformly distributed between 0 and 1. One advantage of Equation (5) is that it does not move particles outside the feasible space. However, Equation (5) does not move each particle exactly in the direction of the force exerted on them, and thus does not closely follow the electromagnetic heuristics. Also notably, the best particle is not moved.
2.2.2. Original Method with a Perturbed Point
Birbil et al. [9] indicated that the original EML method could converge prematurely, and thus they modified the original method by introducing the idea of a perturbed point. The perturbed point, xp is the farthest particle from the current best particle xbest in the current population, i.e.
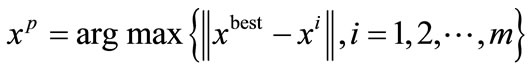 (6)
(6)
Their new method works exactly the same as the original EML method [1] does except that the calculation of the force exerted on xp is modified as follows. First, the force 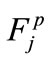 exerted on xp from particle xj is perturbed by multiplying a random value λ ~ U (0, 1), as shown in Equation (7).
exerted on xp from particle xj is perturbed by multiplying a random value λ ~ U (0, 1), as shown in Equation (7).
 (7)
(7)
Then, the force  reverses its direction if λ < ν where ν is a parameter between 0 and 1. Finally, the total force exerted on particle p is calculated using Equation (4).
reverses its direction if λ < ν where ν is a parameter between 0 and 1. Finally, the total force exerted on particle p is calculated using Equation (4).
2.2.3. Debels’s Method
In the original EML method, either with or without using a perturbed point, all particles in a population exert a force on all other particles. Debels et al. [2] proposed a simplified EML method by considering only the force from a randomly chosen particle. This method is adopted as the mutation operation in the hybrid algorithms by Kaelo and Ali [12] and Chang et al. [3].
To calculate the force exerted on a particle xi, another particle xj is selected randomly from the current population. Then, the force exerted on xi from xj is calculated using Equation (8):
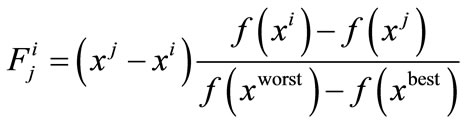 (8)
(8)
where xworst and xbest are the worst particle and the best particle in current population, respectively.
Next, particle xi is moved to . Notably, if f(xi) < f(xj), then it is possible to move xi out of the feasible space of problem (1). An extra step is taken here to restrict xi inside the feasible space using Equation (9).
. Notably, if f(xi) < f(xj), then it is possible to move xi out of the feasible space of problem (1). An extra step is taken here to restrict xi inside the feasible space using Equation (9).
 (9)
(9)
Strictly speaking, this method is not electromagnetismlike because the magnitude of the force  is linear proportional to the distance between xi and xj, not inversely proportional to the square of their distance.
is linear proportional to the distance between xi and xj, not inversely proportional to the square of their distance.
2.2.4. Rocha’s Method of Shrinking Population
Rocha and Fernandes proposed a method to speedup EML algorithms by shrinking the size of a population whenever the spread of the objective values reduces by a predefined percentage [11]. Essentially, this idea can be applied to any population-based evolutionary methods.
The spread of the objective values w.r.t. the best value of a population is defined as follows.
 (10)
(10)
Initially, SPRref is set as the SPR of the initial population. Then, every time after local search in an EML algorithm, if the remaining population size is greater than twice the number of dimensions, then the SPR of the current population is calculated. If the current SPR is less than εSPRref, then half of the population is discarded and SPRref is set to current SPR. Here, ε is a used-defined threshold.
2.2.5. Rocha’s Method of Modified Force
Rocha and Fernandes proposed another EML method which only differs from the original EML method on the calculation of the total force exerted on each particle [13]. This method takes the change of the force into account.
The total force Fi exerted on particle i in the current iteration is calculated as follows. First, Fi is calculated using Equations (2)-(4), as did in the original EML method. Then, the change Δi of the force is set to 0 for the first iteration, and is set to  for the rest iterations of the algorithm, where
for the rest iterations of the algorithm, where  denotes the total force exerted on particle i in the previous iteration. Finally, Fi is adjusted as Fi + βΔi, where β is a parameter in the interval [0, 1). Notably, if β = 0, this method is the same as the original EML method. The suggested value for β is 0.1.
denotes the total force exerted on particle i in the previous iteration. Finally, Fi is adjusted as Fi + βΔi, where β is a parameter in the interval [0, 1). Notably, if β = 0, this method is the same as the original EML method. The suggested value for β is 0.1.
2.2.6. Rocha’s Method of Modified Charge
Rocha and Fernandes proposed two methods that intend to improve the efficiency and solution accuracy of EML algorithms [14]. Both methods differ from the original EML method on how the charge of a particle is calculated. Their first and second methods replace Equation (2) of the original EML with Equations (11) and (12), respectively.
 (11)
(11)
 (12)
(12)
Both Equations (11) and (12) still yield qi between 0 and 1. Furthermore, both methods replace Equation (3) of the original EML with Equation (13) such that the magnitude of the force  exerted on particle xi from particle xj is inversely proportional to the square of the distance between xi and xj to be consistent with the electromagnetism heuristics.
exerted on particle xi from particle xj is inversely proportional to the square of the distance between xi and xj to be consistent with the electromagnetism heuristics.
 (13)
(13)
2.2.7. Yurtkuran’s Method of Reducing Movement
Yurtkuran and Emel [5] propose an EML method that differs from Debels’s method [2] only on how the electromagnetic force moves a particle. Their method reduces the effect of the force as the number of iterations increases. Let iter denote the current number of iterations. After calculating the force  exerted on particle xi from particle xj using equation (8) as did in Debels’s method, xi is moved to
exerted on particle xi from particle xj using equation (8) as did in Debels’s method, xi is moved to  instead of xi +
instead of xi + . Consequently, this method has the effect of reducing the range of movement as the number of iterations increases. As in Debels’s method, this method could move particles out of the feasible space, and thus Equation (9) should be applied to confine particles inside the feasible space.
. Consequently, this method has the effect of reducing the range of movement as the number of iterations increases. As in Debels’s method, this method could move particles out of the feasible space, and thus Equation (9) should be applied to confine particles inside the feasible space.
2.2.8. Shang’s Method of High Charged Particles
Shang et al. proposed an EML method that ignores the force exerted from those particles with small charges to improve efficiency [15]. First, the charge of each particle is calculated using Equation (2), as did in the original EML method. Those particles with charges lower than half of the average charge of all particles cannot exert force on other particle. This can be done by introducing a modified charge  of particle xi as follows.
of particle xi as follows.
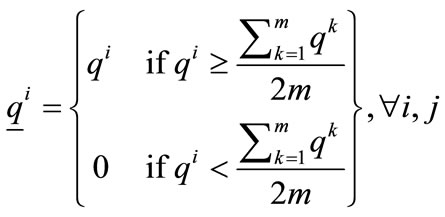 (14)
(14)
Then, Equation (15) is used to calculate the force  exerted on particle xi from particle xj.
exerted on particle xi from particle xj.
 (15)
(15)
Equation (15) does not closely follow the electromagnetic heuristics. The rest of this method is the same as the original EML method. The composite force Fi exerted on particle xi is calculated using Equation (4), and the new position of particle xi is calculated using Equation (5).
3. A Sanity Test for Premature Convergence
Birbil and et al. [9] used a simple example to show the premature convergence problem of the original EML algorithm of Birbil and Fang [1], described in Section 2.2.1. In this section, we adopt the same example and show that all the EML variants described in Sections 2.2.3 - 2.2.8 suffer from the same problem.
Consider the objective function f(x), shown in Figure 3,

Figure 3. Premature convergence of EML alogorthms.
for a one dimensional minimization problem. Supposed that all of the particles (shown as solid circles) in the current population are located on the right of the position marked with a star. Let xi and xj be two particles in the population. No matter xj is on the left or on the right of xi, the direction of the force exerted on xi from xj is toward the right, according to Equation (3), (8), (13) or (15). Consequently, the electromagnetic force will always move all particles, excluding the best particle, in the current population to the right, and miss the global optimum on the left at the origin.
Birbil and et al. [9] proved that their perturbed EML method, described in Section 2.2.2, terminates with an “ε-optimal” solution when the number of iterations is large enough. This is achieved by stochastically reversing the direction of the electromagnetic force exerted on the particle (called the perturbed particle) that is farthest from the current best particle. For the example in Figure 3, it is obvious that the perturbed particle is the leftmost particle in the population, and it could be moved to the left of the star sign, and consequently converges to the origin, using the perturbed EML method.
Consider another example in Figure 4, where the perturbed particle is the rightmost particle in the population, and the current best particle is the second leftmost particle. In this case, the reversed electromagnetic force does not help because if the perturbed particle is moved by its reversed electromagnetic force, it will be moved to the right, and consequently further away from the origin.
If the perturbed particle (or any particle on the right of the current best particle) in Figure 4 is moved by its electromagnetic force, it will be moved to the left. However, this movement is beneficial only if the particle can be moved pass the star sign. In other words, the electromagnetic force provides the direction of movement, but the distance of the movement should not be restricted to the distance between the particle and the current best particle. For example, Equation (5) provides the greatest freedom by allowing the movement up to the boundary of the feasible space. However, such freedom also reduces the convergence speed to the global optimum, and makes the direction of the movement somewhat different from the direction of the electromagnetic force. On the other hand, Debel’s method, described in Section 2.2.3, provides less freedom by restricting the distance of

Figure 4. Example of a useless perturbed particle.
the movement up to the distance between the two particles under consideration. Therefore, it is more likely to trap in a local optimum.
4. Performance Study
4.1. Experimental Setting
Since our interest is on the various interpretations of the electromagnetic heuristics, all methods, described in Section 2, except the shrinking population method are implemented for this study. The shrinking population method is not included because its idea is applicable to any population-based evolutionary algorithm. For ease of exposition, the seven implemented methods are listed in Table 1.
Furthermore, the idea of the perturbed point method [9], described in Section 2.2.2, is extended to and implemented as an option for all seven methods in Table 1. Local search for the current best particle is also implemented as an option. Therefore, method 2 refers to Debel’s method without perturbed point and local search; method 2P refers to Debel’s method with perturbed point but without local search; method 2L refers to Debel’s method with local search but without perturbed point.
A set of six well-known benchmark functions, listed in Table 2, was used in this experiment. The number n of dimensions ranges from 10 to 50. The first benchmark function is unimodal, while the remaining five are multimodal. The number of particles and the maximum number of iteration are set to 2n and 25n, respectively.
For each setting, 30 runs were conducted, and their average performance was obtained. Each run stops until the maximum number of iterations is reached. For the same run, the same set of initial particles was generated for all methods. This performance study is divided into three parts, which are described in the subsequent three sections.
4.2. Heuristic Test
This section focuses on the effectiveness of various
simulations of the electromagnetic heuristics, and ignores the impact of using a perturbed point and local search. Specifically, we compare the EML methods with both perturbed point and local search deactivated, i.e. methods 1-7.
Figure 5 shows how the best objective value converges for all seven methods for the first run of benchmark function f6 with n = 10. Method 6 quickly stuck in a poor local optimum. Recall from Section 2 that methods 2 and 6 consider the force exerted on a particle only from another randomly chosen particle, while the rest five methods consider the force from all other particles. This explains why method 2 converges at a slower pace than the other five methods did. Similar results can be observed on the other benchmark functions and different number of dimensions.
Tables 3-7 show the average of the best objective values over 30 runs. Method 6 is the worst performer,
since its results are very far from that of the other methods. Overall, method 4 achieved the best results among the seven methods. However, the results are still far from the known best objective values, shown in the third column of Table 2. According to this performance study, EML algorithms with both perturbed point and local search deactivated perform poorly for most benchmark functions, and thus are not recommended. Previous work has shown that local search and perturbed point help improving the performance of EML methods.

Table 3. Average of best objective values (n = 10).

Table 4. Average of best objective values (n = 20).

Figure 5. Convergence of EML methods for f6 with n = 10.

Table 5. Average of best objective values (n = 30).

Table 6. Average of best objective values (n = 40).

Table 7. Average of best objective values (n = 50).
Subsequent two sections study their impact on the performance.
4.3. Local Search Test
Birbil and Fang [1] suggested that applying local search on the current best particle improves the performance of their EML method without incurring much overhead. This section evaluates the performance of the seven EML methods with local search on the best particle. We adopted the same local search method as Birbil and Fang [1] did, i.e. random line search, described in Figure 2.
The two parameters for random line search are set as follows: δ = 1E−3 or 1E−4 and LsIter = 150. No attempt is made to fine tune these two parameters to fit different benchmark functions. Notably, for an EML method without local search, the objective function needs to be calculated m − 1 times in each iteration, where m is the number of particles in the population. With local search on the best particle, this number becomes m − 1 + n × LsIter, where n is the number of dimensions. When n × LsIter > m − 1, the time spent on local search surpasses that on the electromagnetic heuristics.
Figure 6 shows how the best objective value converges for all seven methods for the first run of benchmark function f6 with n = 10 and δ = 1E−3. methods 6L, 7L and 2L converged slower than the other methods did.

Table 8. Average of best objective values (n = 10, δ = 1E−3).

Figure 6. Convergence of EML methods with local search for f6 with n = 10.

Table 9. Average of best objective values (n = 20, δ = 1E−3).

Table 10. Average of best objective values (n = 30, δ = 1E−3).

Table 11. Average of best objective values (n = 40, δ = 1E−3).

Table 12. Average of best objective values (n = 50, δ = 1E−3).
Tables 8-12 show the average of the best objective values over 30 runs when δ = 1E−3. Similar to the previous test, method 6L is the worst performer. Comparing the results in Tables 8-12 to their counterparts in Tables 3-7, local search on the best particles improves the results in most cases but with some exceptions shown in italicized font in Tables 8-12. We reduced the parameter δ from 1E−3 to1E−4, and repeated the same experiment. The results are shown in Tables 13-17. With δ = 1E−4, almost all methods with local search yield

Table 13. Average of best objective values (n = 10, δ = 1E−4).

Table 14. Average of best objective values (n = 20, δ = 1E−4).

Table 15. Average of best objective values (n = 30, δ = 1E−4).

Table 16. Average of best objective values (n = 40, δ = 1E−4).

Table 17. Average of best objective values (n = 50, δ = 1E−4).
better results than their counterparts without local search, with few exceptions of method 2L on f5 for n = 10 to 50 and on f4 for n = 10.
According to Tables 8-17, method 6L remains the worst, and method 2L performs poorly on many instances. Although no single method performs the best on all instances, methods 4L and 5L appear to be the top two performers. method 1L also does well on some instances.
4.4. Perturbed Point Test
As described in Section 2.2.2, Birbil et al. [9] proposed a new EML method that modifies the original EML method using a perturbed point. Since the original EML method is denoted as method 1 in Table 1, the new method is denoted as method 1P herein. Both methods differ only on how the force exerted on the perturbed particle is calculated.
Based on the same idea, methods 2-7 are modified to use the perturbed particle, and the resulting methods are denoted as methods 2P-7P. Notably, these perturbed methods calculates the objective function the same number of times as their non-perturbed counterparts do.
The parameter ν, defined in Section 2.2.2, for these perturbed methods is set to 0.5 in this test. Tables 18-22 show the performance results of these perturbed methods.

Table 18. Average of best objective values (n = 10, perturb).

Table 19. Average of best objective values (n = 20, perturb).

Table 20. Average of best objective values (n = 30, perturb).

Table 21. Average of best objective values (n = 40, perturb).

Table 22. Average of best objective values (n = 50, perturb).
Among them, method 4P appears to perform the best for n ≤ 30, while methods 5P-7P perform the best for n > 30.
However, when comparing to their non-perturbed counterparts in Tables 3-7, these perturbed methods often yield no improvement (shown in italicized font in Tables 18-22), especially for n ≤ 30. Although these perturbed methods have a better chance to escape from local optimums, they often require much more iterations to reach the global optimum. Since the maximal number of iterations is set to 25n, where n is the number of dimensions, these perturbed methods might not yet experience the benefit of a perturbed particle when n is not large enough.
5. Conclusions
This paper studies various interpretations of the electromagnetic heuristics in EML algorithms. Our results show that EML methods without local search and perturbed point often yield poor results, especially for methods 2 and 6. Notably, methods 2 and 6 differ from other EML methods in two aspects. Firstly, they consider the electromagnetic force from only one randomly chosen particle instead of all other particles. Secondly, they move particles in a less free manner than the other methods do. Specifically, with method 2, when particle i exerts a force to move particle j, the distance of this movement is restricted to no greater than the distance between particles i and j. The distance of this movement is even smaller with method 6. Further experiment is needed to find the culprit for their poor performance. Notable, even using either perturbed point or local search, methods 2P, 2L, 6P and 6L still yield unstable results.
Strictly following the electromagnetic heuristics does not guarantee better performance. Actually, no single interpretation of the electromagnetic heuristics consistently performs better than other interpretations. On notable example is method 4, which appears to be the best method with no local and perturbed point. However, its perturbed version, method 4P, becomes quite unstable. Overall, these perturbed methods often yield poorer results than their un-perturbed counterparts do. Therefore, improving the perturbed technique and integrating various EML methods are future research topics.
6. Acknowledgements
This research is supported by National Science Council under Grant NSC 99-2221-E-155-048-MY3, and by the Bureau of Energy, Ministry of Economic Affairs, Taiwan, under the project of The Study of Associative Decoupling Algorithms.