Theoretical Analysis of Mass Transfer with Chemical Reaction Using Absorption of Carbon Dioxide into Phenyl Glycidyl Ether Solution ()
1. Introduction
Carbon dioxide is generally a useful gas that is made up of a carbon atom and two oxygen atoms. It is very important in plant photosynthesis, manufacturing carbonated soft drinks, powering pneumatic systems in robots, used in fire extinguisher, removing caffeine from coffee, etc., Carbon dioxide has the potential to provide a vast and cheap source of carbon. Turning it into useful products would also reduce its environmental impact as a greenhouse gas. Scientists have shown that ionic liquids are selective catalysts for converting carbon dioxide into synthetic intermediates called cyclic carbonates, but it is difficult to separate and recycle the liquid catalyst.
Recently, the chemical fixation of carbon dioxide has become an important research topic [1], because of the danger posed by global warming, and conversion of carbon dioxide into valuable substances is an extremely attractive solution. The reaction with oxiranes leading to five-membered cyclic carbonate (oxirane-reaction) is wellknown among many examples [2,3]. These carbonates can be used as aprotic polar solvent and sources for polymer synthesis [4]. In the oxirane-reaction, high pressure (5 - 50 atm) of CO2 has been thought to be necessary [2]. The oxirane—reactions under atmospheric pressure have been reported [4].
Many organic and inorganic compounds including ammines, phosphines, quaternary ammonium salts, and alkali metal salts are known to catalyze the oxiranereaction [3]. The kinetics of the reaction between CO2 and phenyl glycidyl ether (PGE) have been studied using catalyst THA-CP-MS41, The reaction rate constants were obtained using the measured absorption rate of and analyzed with the mass transfer mechanism associated with the chemical reactions.
Park et al. [5] investigated the chemical absorption of carbon dioxide and phenyl glycidyl ether solution containing the catalyst THA-CP-MS41 in a heterogeneous system. To our knowledge no analytical solutions of this model have been reported. The purpose of this communication is to derive simple approximate analytical expression for the steady-state concentrations of CO2, PGE and flux using the Adomian decomposition method.
2. Mathematical Formulation of the Problem and Analysis
Figure 1 shows the schematic representation of the stirred-cell absorber [5]. The overall reaction between CO2 and phenyl glycidyl ether (PGE) to form the 5—membered cyclic carbonate is as follows:
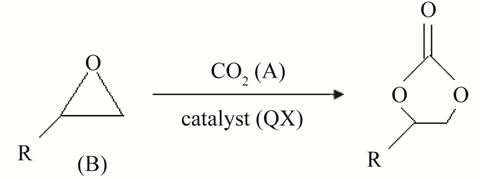 (1)
(1)

Figure 1. Shows the schematic representation of the stirredcell absorber [5]. A, B, C: Valve; D: Absorber; E: Impeller; F: Liquid bottle; G: Funnel; H: Soap film meter; I: Gas chromatography.
where R is a functional group of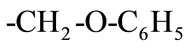 . The overall reaction of Equation (1) consists of two conescutive steps: 1) a reversible reaction between PGE (B) and THA-CP-MS41 (QX) to form an intermediate complex (C1); 2) an reversible reaction between C1 and CO2 (A) to form QX and five-membered cyclic carbonate (C):
. The overall reaction of Equation (1) consists of two conescutive steps: 1) a reversible reaction between PGE (B) and THA-CP-MS41 (QX) to form an intermediate complex (C1); 2) an reversible reaction between C1 and CO2 (A) to form QX and five-membered cyclic carbonate (C):
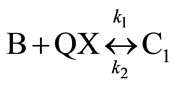 (2)
(2)
 (3)
(3)
At steady state condition, the consecutive chemical reaction rate of CO2 to form C1 is given as follows:
 (4)
(4)
where, St is the surface area of catalyst,  are the concentration of CO2 and PGE respectively. K1 is the reaction equilibrium constant, k1 is the forward reaction rate constant in Equation (2) and k3 is the forward reaction rate constant in Equation (3). The mass balances of CO2 and PGE, using film theory accompanied by the consecutive chemical reactions are given as follows [5]:
are the concentration of CO2 and PGE respectively. K1 is the reaction equilibrium constant, k1 is the forward reaction rate constant in Equation (2) and k3 is the forward reaction rate constant in Equation (3). The mass balances of CO2 and PGE, using film theory accompanied by the consecutive chemical reactions are given as follows [5]:
 (5)
(5)
 (6)
(6)
where DA and DB are the diffusivity of CO2 and PGE respectively and z is the distance. The boundary conditions are:
 (7)
(7)
Equations (5), (6) and the boundary conditions (7) can be normalized by employing the following parameters:
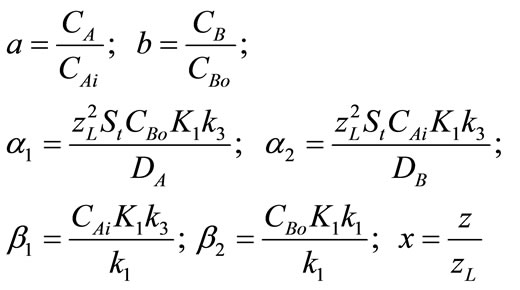
where, a, is the concentration of CO2, b is the concentration of PGE,  normalized parameters and x is the dimensionless distance. Now the two nonlinear reaction/diffusion Equations (5), (6) in normalized form becomes as follows:
normalized parameters and x is the dimensionless distance. Now the two nonlinear reaction/diffusion Equations (5), (6) in normalized form becomes as follows:
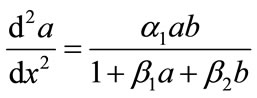 (8)
(8)
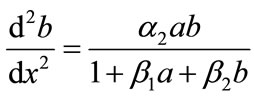 (9)
(9)
The above Equations (8), (9) are the system of nonlinear differential equations. While no general method of solving these nonlinear problems has been proposed, several vigorous procedure such as Adomian decomposition method [6-10], Homotopy perturbation method [11- 15] and Homotopy analysis method [16-21] etc., have been analyzed. Here, Adomian decomposition method is used to solve these nonlinear differential equations. The boundary conditions becomes,
 (10)
(10)
where,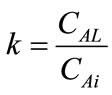 . The enhancement factor of CO2, defined as the ratio of the flux of CO2 with chemical reaction to that without chemical reaction is as follows,
. The enhancement factor of CO2, defined as the ratio of the flux of CO2 with chemical reaction to that without chemical reaction is as follows,
 (11)
(11)
3. Analytical Solutions of Concentrations of CO2 and PGE under Steady-State Condition Using the Adomian Decomposition Method
In this paper, the Adomian decomposition method (see Appendix A) is used to solve nonlinear differential equations. The ADM [6-10] yields, without linearization, perturbation or transformation, an analytical solution in terms of a rapidly convergent infinite power series with easily computable terms. The basic principle of this method is described in Appendix A and detailed derivation of dimensionless concentration of CO2 and PGE, from the nonlinear Equations (8) and (9) are described in Appendix B. Using this method (refer Appendix B), we obtain the analytical expression corresponding to the concentrations of CO2 and PGE as follows:
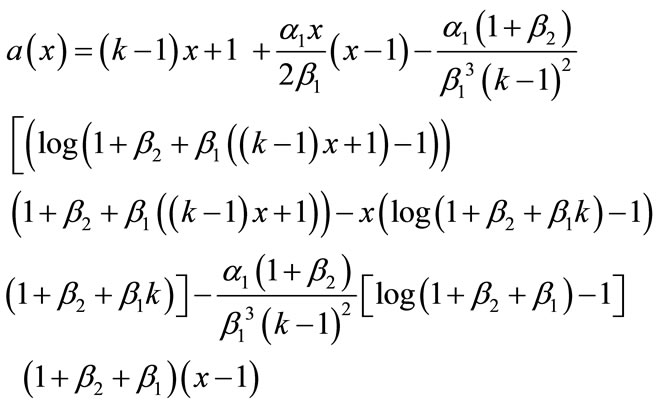 (12)
(12)
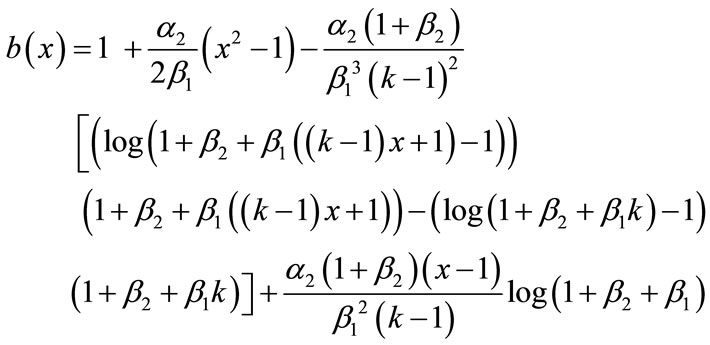 (13)
(13)
From Equation (11), we obtain the flux as
 (14)
(14)
4. Numerical Simulation
The function pdex4 in Scilab/Matlab software which is a function of solving the initial-boundary value problems for the two reaction/diffusion equations is used to solve Equations (8) and (9). The normalized concentrations of CO2 and PGE are compared with simulation results in Figures 1 and 2. A satisfactory agreement is noted. The Scilab/Matlab program is also given in Appendix C. In Table 1, the simulation results compared with ADM results, the maximum error is 0.64%.
5. Results and Discussion
Equations (12) and (13) represent the new closed and simple approximate analytical expressions of the normalized concentrations of CO2 and PGE for all values of parameters  and k. The current response is given in Equation (14). The concentration profiles of CO2 and PGE are shown in Figures 2 and 3. The concentration of CO2 increases when the normalized parameter k increases (refer Figure 2(a)). The concentration of CO2 decreases when the parameters
and k. The current response is given in Equation (14). The concentration profiles of CO2 and PGE are shown in Figures 2 and 3. The concentration of CO2 increases when the normalized parameter k increases (refer Figure 2(a)). The concentration of CO2 decreases when the parameters  increases (refer Figures 2(b) and (c)). In Figure 3, the concentration of PGE decreases when the normalized parameter
increases (refer Figures 2(b) and (c)). In Figure 3, the concentration of PGE decreases when the normalized parameter  or surface area of catalyst increases and diffusivity of PGE decreases. Equation (14) represents the normalized flux. The value of flux increases as the parameters
or surface area of catalyst increases and diffusivity of PGE decreases. Equation (14) represents the normalized flux. The value of flux increases as the parameters  or reaction equilibrium constant increases (refer Figures 4(a) and (b)). In Figure 4(c), the value of flux decreases as the parameters
or reaction equilibrium constant increases (refer Figures 4(a) and (b)). In Figure 4(c), the value of flux decreases as the parameters 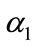 or or surface area of catalyst increases and diffusivity of CO2 decreases.
or or surface area of catalyst increases and diffusivity of CO2 decreases.
6. Conclusions
This paper presents a theoretical treatment of carbon dioxide and phenyl glycidyl ether solution in chemical reaction. Also, we have discussed the mathematical models of CO2 absorption into the PGE solution. We have solved the nonlinear differential equations both analytically and numerically. The approximate analytical expressions for
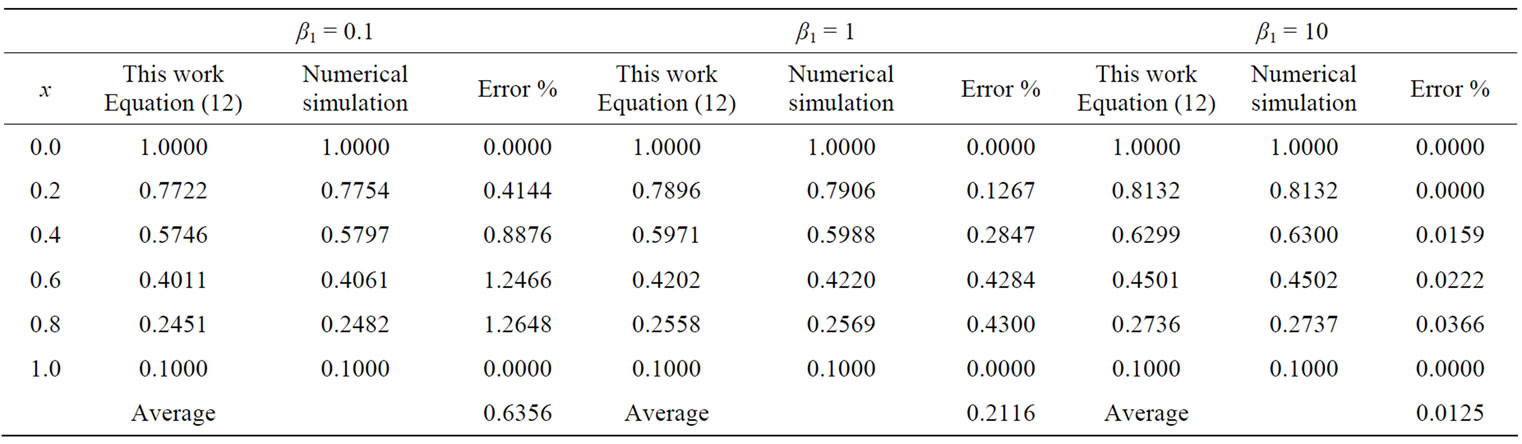
Table 1. Comparison of normalized substrate concentration of CO2 (A(x)) between Equation (12) and numerical simulation for various values of parameters β1 when α1 = 1, β2 = 0.001, k = 0.1.
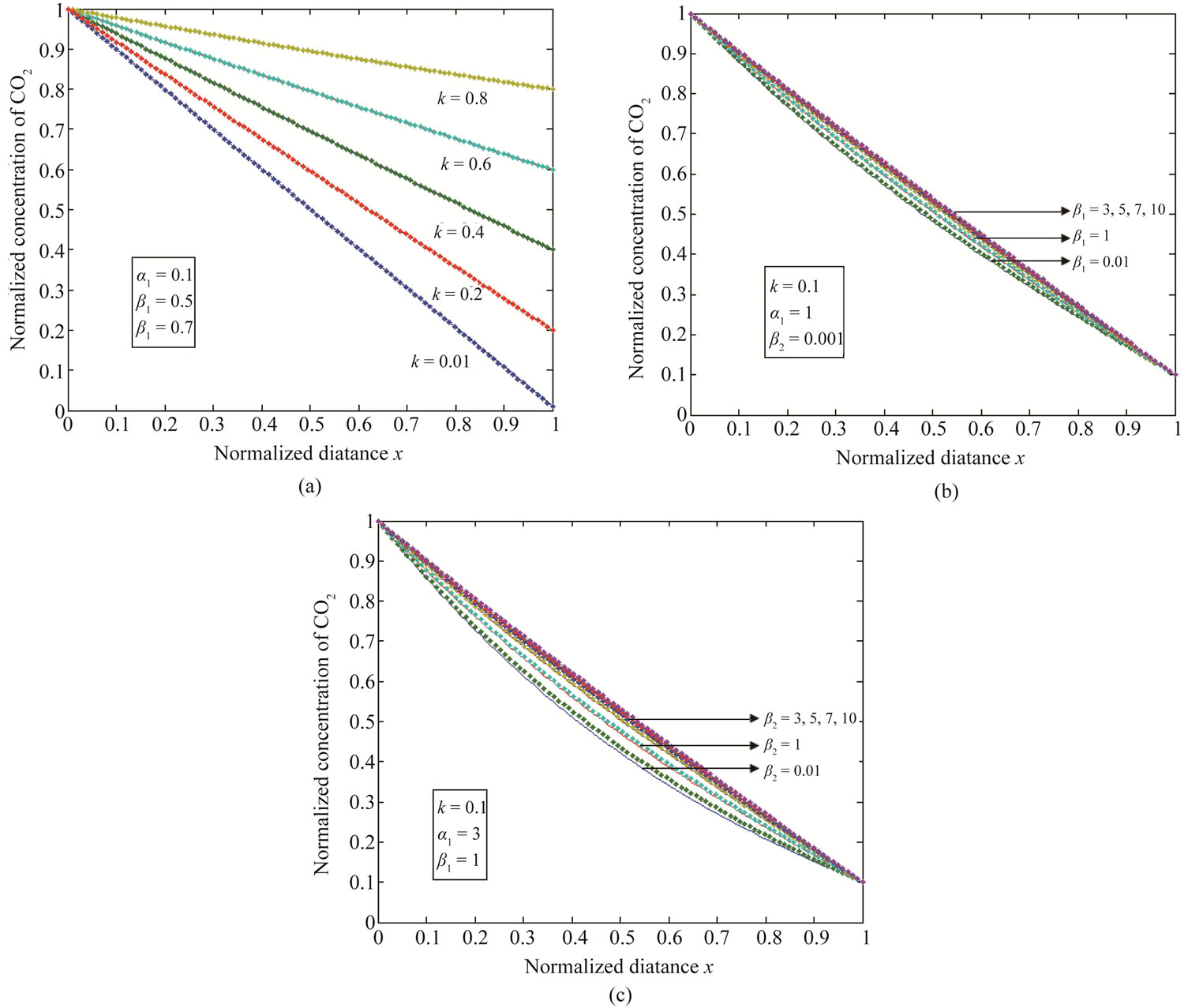
Figure 2. Normalized concentration of CO2 for various values of parameters is plotted using Equation (12). (a) α1 = 0.1, β1 = 0.5, β2 = 0.7; (b) k = 0.1, α1 = 1, β2 = 0.001; (c) k = 0.1, α1 = 3, β1 = 1. The key to the graph (stacked line) represents the Equation (12) and (dotted line) represents the numerical simulation.

Figure 3. Normalized concentration of PGE for various values of parameters is plotted using Equation (13). The key to the graph (stacked line) represents the Equation (13) and (dotted line) represents the numerical simulation.
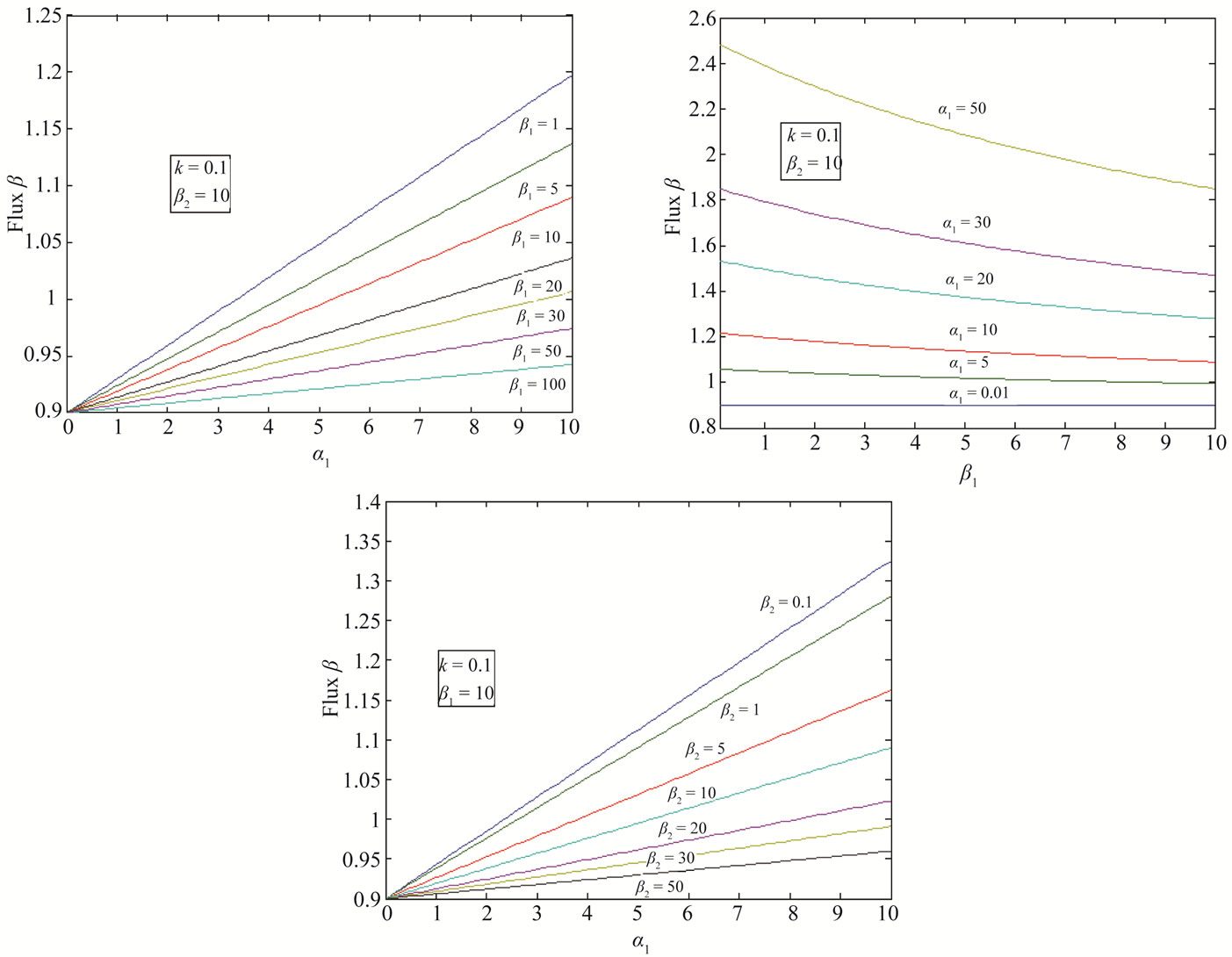
Figure 4. Diagrammatic representation of the normalized flux β for various values of α1, β1, β2 and k.
the steady state concentrations of CO2 and PGE for all values of parameters using the Adomian decomposition method. These theoretical results are useful to evaluate the overall reaction rate constant and enhancement factor of CO2. A satisfactory agreement with the numerical result is noted.
7. Acknowledgements
This work was supported by the University Grants Commission (F. No. 39-58/2010(SR)), New Delhi, India. The authors are thankful to Dr. R. Murali, The Principal, The Madura College, Madurai and Mr. M. S. Meenakshisundaram, The Secretary, Madura College Board, Madurai for their encouragement. The author S. Muthukaruppan is very thankful to the Manonmaniam Sundaranar University, Tirunelveli for allowing to do the research work.
Appendix A
Basic Concept of the Adomian Decomposition Method (ADM)
Adomian decomposition method [22-27] depends on decomposing the nonlinear differential equation
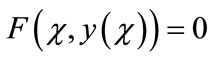 (A.1)
(A.1)
into the two components
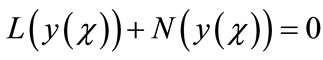 (A.2)
(A.2)
where L and N are the linear and the nonlinear parts of F respectively. The operator L is assumed to be an invertible operator. Solving for L(y(χ)) leads to
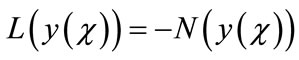 (A.3)
(A.3)
Applying the inverse operator L on both sides of Equation (A.3) yields
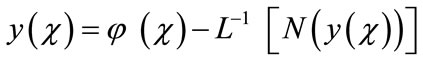 (A.4)
(A.4)
where 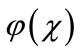 is a function that satisfies the condition
is a function that satisfies the condition . Now assuming that the solution y can be represented as infinite series of the form,
. Now assuming that the solution y can be represented as infinite series of the form,
 (A.5)
(A.5)
where
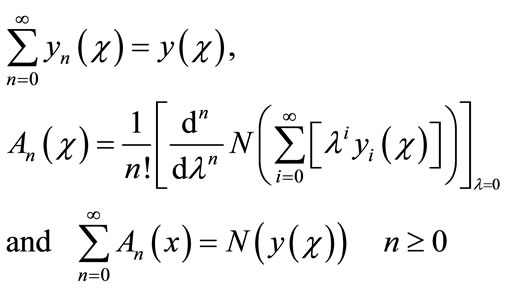 (A.6)
(A.6)
Then equating the terms in the linear system of Equation (A.5) gives the recurrent relation
 (A.7)
(A.7)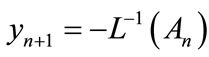

However, in practice all the terms of series in Equation (A.5) cannot be determined, and the solution is approximated by the truncated series .
.
Appendix B
Analytical Expression of Concentrations of CO2 and PGE Using the Adomian Decomposition Method
To solve Equations (8) and (9) using the Adomian decomposition method, we write the Equations (8) and (9) in the operator form,
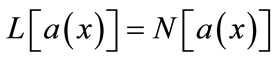 (B.1)
(B.1)
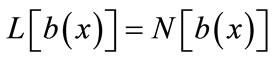 (B.2)
(B.2)
where
 (B.3)
(B.3)
Applying the inverse operator 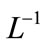 on both sides of Equation (B.1) and (B.2) yields
on both sides of Equation (B.1) and (B.2) yields
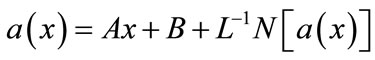 (B.4)
(B.4)
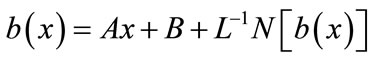 (B.5)
(B.5)
According to the ADM, the solution a(x) and b(x) can be elegantly computed by using the recurrence relation
 (B.6)
(B.6)
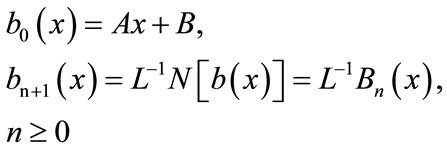 (B.7)
(B.7)
where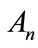 and Bn are the Adomian polynomials of
and Bn are the Adomian polynomials of  respectively. We can find the first few Adomian polynomial coefficients
respectively. We can find the first few Adomian polynomial coefficients 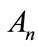 and Bn using Equation (A.6) as follows:
and Bn using Equation (A.6) as follows:
 (B.8)
(B.8)
 (B.9)
(B.9)
The remaining polynomials  can be generated easily, using Equation (A.6). Applying the following boundary conditions
can be generated easily, using Equation (A.6). Applying the following boundary conditions
 (B.10)
(B.10)
 (B.11)
(B.11)
From Equations (B.6) and (B.7) using the above conditions we obtain the following results:
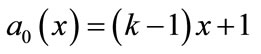 (B.12)
(B.12)
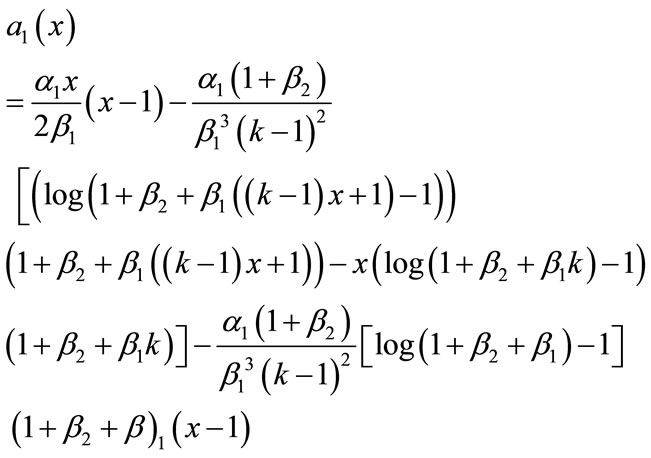 (B.13)
(B.13)
 (B.14)
(B.14)
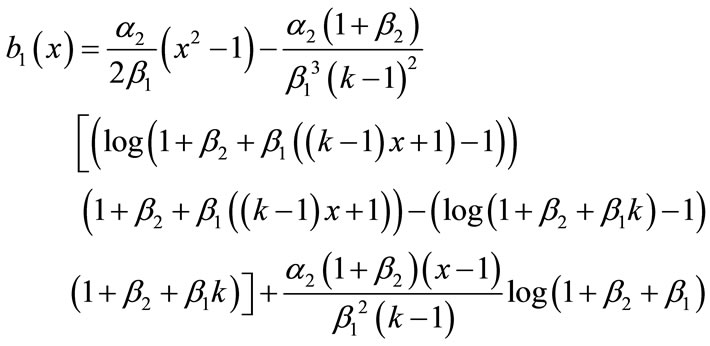 (B.15)
(B.15)
Adding Equations (B.12) and (B.13), (B.14) and (B.15), we get the concentration of CO2 and PGE (Equations (12) and (13)) in the text.
Appendix C
Scilab/Matlap program for the numerical solution of the system of nonlinear Equations (8) and (9)
function pdex4 m = 0;
x = linspace(0,1);
t=linspace(0,100000);
sol = pdepe(m,@pdex4pde,@pdex4ic,@pdex4bc,x,t);
u1 = sol(:,:,1);
u2 = sol(:,:,2);
figure plot(x,u1(end,:))
title('u1(x,t)')
xlabel('Distance x')
ylabel('u1(x,2)')
figure plot(x,u2(end,:))
title('u2(x,t)')
xlabel('Distance x')
ylabel('u2(x,2)')
function [c,f,s] = pdex4pde(x,t,u,DuDx)
c = [1; 1];
f = [1; 1] .* DuDx;
a=0.001;
b=10;
M=10;
N=0.01;
F=-(a*u(1)*u(2))/(1+(M*u(1))+(N*u(2)));
F1=-(b*u(1)*u(2))/(1+(M*u(1))+(N*u(2)));
s=[F; F1];
function u0 = pdex4ic(x);
u0 = [1; 1];
function [pl,ql,pr,qr]=pdex4bc(xl,ul,xr,ur,t)
pl = [ul(1)-1;0];
ql = [0; 1];
pr = [ur(1)-0.1; ur(2)-1];
qr = [0; 0];
Appendix D
Nomenclature
Symbols CA: Concentration of CO2 (M)
CB: Concentration of PGE (M)
DA: Diffusivity of CO2 (m2/s)
DB: Diffusivity of PGE (m2/s)
K1: Reaction equilibrium constant (1/M)
k1: Forward reaction rate constant in reaction Equation (2) (1/m2s)
k2: Backward reaction rate constant in reaction Equation (2) (M/m2s)
k3: Forward reaction rate constant in reaction Equation (3) (1/m2s)
rA,cons: Reaction rate of CO2 in consecutive reaction model (M/s)
St: Surface area of catalyst (m2)
z: Distance (m)
zL: Film thickness (m)
a: Normalized concentration of CO2 (Dimensionless)
b: Normalized concentration of PGE ( Dimensionless )
 : Normalized parameters (Dimensionless)
: Normalized parameters (Dimensionless)
 : Flux of CO2 (Dimensionless)
: Flux of CO2 (Dimensionless)
Subscripts A: CO2
B: PGE L: Bulk solution o: Feed or solvent
NOTES