Can We Form Gravitinos by Something Other Than a Higgs Boson in the Electro-Weak Era? ()
1. Introduction
We will ask the question here. In an earlier document, the author presented an equivilence between Gravitinos in the electro weak era, and Gravitons today. The motivation of using two types of Machs principle, one for the Gravitinos in the electro weak era, and then the 2nd modern day Mach’s principle, as organized by the author are as seen in [1]
 (1)
(1)
are really a statement of information conservation. What we now ask is if the Gravitino can be re stated in terms in fidelity to quantum mechanics, or if some other theoretical constuction must be used. The motivation for asking this question will be seen in examining if the Gravitino, as in the mass in the left hand side of Equation (1), as it materializes due to Comay’s [2] presentation as to defects in the Higgs equation of state, is in fidelity with QM principles. If not, then what would replace it?
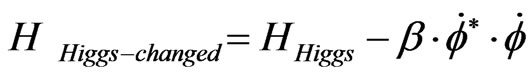 (2)
(2)
And
 (3)
(3)
In fidelity with the physics evolution of
 (4)
(4)
Whereas what is observed is, instead [2]
 (5)
(5)
To further elucidate this question, we will also ask if there is a way to encapsulate  in Equation (2) above in the methodology of constucting QM within a larger, semi classical theory. As given in the 5th Dice 2010 work shop, as given by Elze, Gambarotta and Vallone [3] there is a speculated ensemble theory involving a “Liouville superator”
in Equation (2) above in the methodology of constucting QM within a larger, semi classical theory. As given in the 5th Dice 2010 work shop, as given by Elze, Gambarotta and Vallone [3] there is a speculated ensemble theory involving a “Liouville superator”  of
of
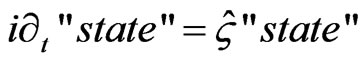 (6)
(6)
The end result is, after a Fourier transform re casting the Equation (6) in terms of a matrix equation looking like
 (7)
(7)
We will discuss Equation (7) in a generalized incantation in APPENDIX A which will show as that the quantum mechanics type interactions require a most specialized potential, as either a constant, or a Harmonic potential, with others not sutiable, if we wish to extract quantum mechanics from the results of Equation (7), and from there to comment upon candidate equations which may be a way to contain  as far as a generalized theory which may contain QM (Dirac) type behavior. If not, then Equation (2) does not qualify as far as having
as far as a generalized theory which may contain QM (Dirac) type behavior. If not, then Equation (2) does not qualify as far as having  reduced to a quantum mechanica subset and we must then go to the Comay description of the Higgs equation used to define the creation of/evolution of the Gravitino as faulty physics, needing an abrupt fix to reduce it to the form of Equation (2) to salvage quantum mechanics.
reduced to a quantum mechanica subset and we must then go to the Comay description of the Higgs equation used to define the creation of/evolution of the Gravitino as faulty physics, needing an abrupt fix to reduce it to the form of Equation (2) to salvage quantum mechanics.
Appendix B brings up the relevance of the Dirac eqjatkl to the critique which Comay [2] brings to the discussion of a proper equation for a well behaved experimentally verified equation. We add an example of how early universe Lorentz violation is equivilent to the break up of the fidelity of the Higgs term, and in fact, the Equation (B12) presented in Appendix B is in its behavior (if it were 10 orders of magnitude larger, i.e. as a Torsion term added in) very similar to the problem outlined in equation( B6) in the Higgs potential, i.e. note in Equation (B3) with the unwanted 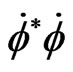 term which blocks the Higgs equation of state from having the good behavior postulated by Comay [2] in his Claims 1, 2 and 3 as given in Appendix B below. Note also that the problem as outlined in
term which blocks the Higgs equation of state from having the good behavior postulated by Comay [2] in his Claims 1, 2 and 3 as given in Appendix B below. Note also that the problem as outlined in  term shows up in an even more glaring fashion in the incredibly complicated Lagrangian specified for the formation of Gravitinos in the early universe. We will get to that next. It is useful to compare these ideas with what J. Lee published recently [4].
term shows up in an even more glaring fashion in the incredibly complicated Lagrangian specified for the formation of Gravitinos in the early universe. We will get to that next. It is useful to compare these ideas with what J. Lee published recently [4].
2. Examining the Formation of Gravitinos in the Early Universe
In [5] the density is given by, if  is for early universe degrees of freedom
is for early universe degrees of freedom
 (8)
(8)
With a resulting Hubble rate for the radiation era as written as for , radiation era, as
, radiation era, as
 (9)
(9)
The early Gravitino relic density is then given by an expression
 (10)
(10)
times 
This is, in terms of re heating temperature very close to linear in growth due to scaling with a re heating temperature . One obtains an approximately linear growth rate in terms of gravitino density with a most complicated Lagrangian density function which is in the top of Section 2.2. of [5] is so complicated that one cannot, even in linear approximations of it get either a classical or a quantum analogy in terms easily identifiable terms of page 5 of this Ph.D. dissertation. We will review in Appendix A the DICE 2010 [3] article treatment of quantum mechanics in a larger non linear theory [3], and in Appendix B the Comay [2] treatment in terms of lagrangian density both for the Dirac Eq, and also for the Higgs, and then from there make the case necessary as to if the Gravititino is quantum mechanical in its construction or not.
. One obtains an approximately linear growth rate in terms of gravitino density with a most complicated Lagrangian density function which is in the top of Section 2.2. of [5] is so complicated that one cannot, even in linear approximations of it get either a classical or a quantum analogy in terms easily identifiable terms of page 5 of this Ph.D. dissertation. We will review in Appendix A the DICE 2010 [3] article treatment of quantum mechanics in a larger non linear theory [3], and in Appendix B the Comay [2] treatment in terms of lagrangian density both for the Dirac Eq, and also for the Higgs, and then from there make the case necessary as to if the Gravititino is quantum mechanical in its construction or not.
3. Getting the Template as to Keeping Information Content Avaiable for Equation (10) Right and Its Implications for Equation (1) and Equation (4), and Equation (5). Yielding a New Expression of Gravitino Mass in the EW Regime?
The Machian hypothesis and actually Equation (10) are a way to address a serious issue, i.e. how to keep the consistency of physical law intact, in cosmological evolution [1]. Another significant issue is the following. How to reconcile the Comay hypothesis [2] and postulates, as given in Appendix B, and also the DICE 2010 delination of QM as in Appendix A either requiring a zero valued potential, a constant potential, or a potential with quadratic flavor to delineate clear quantum mechanical behavior [3]. If these potential field requirements are not met, as given by Appendix A [3], then one has to ask if a Higgs mechanism in fidelity with Appendix B [2] can be constructed for an allegedly optimal experimental modeling of mass formation.
Equation (10), which has neither a zero valued potential, a linear or a quadratic potential is clearly NOT in sync with the DICE 2010 Appendix A treatments leading to quantum mechanics, alone [3].
Equation (10) does NOT have fidelity with the sort of Comay criteria [2] as given in Appendix B as to a potential energy which is most likely to have optimal match up with experimental data as cited by the Dirac equation results as given in the Comay article.
Either Equation (10) signifies that there is no match up with the sort of evolution equation (for creation of a Gravitino in the electro weak era) as exemplified by the Dirac Equation which Comay likes so much [2], or we have to go to live with the results as given by Appendix B, that what we are seeing in the Gravitino in the Electro weak era is quantum mechanics contained in a larger non linear theory, as Elze seem to be inferring [3] as brought up in Appendix A.
4. Another Approach. How about a New Method for Obtaining in the Electroweak Era Mass without the Higgs?
What we can look at is the Glinka-Beckwith [6] proposal as to a new mass formation process,which may show a different way to examine potential systems, as opposed to the either-or criteria as given by Appendix A [3] and Appendix B [2] below. To do so, note that the article as given in.
 (11)
(11)
We can treat the k as a wave “vector”, and look at the term  as an energy term. Dependent upon how we interpret
as an energy term. Dependent upon how we interpret , i.e. as a per unit interpretation of energy, we could reconcile a treatment of a physically averaged out quantity of the potential energy as given in [5] is contained via the correct effective Lagrangian for light gravitinos
, i.e. as a per unit interpretation of energy, we could reconcile a treatment of a physically averaged out quantity of the potential energy as given in [5] is contained via the correct effective Lagrangian for light gravitinos , which is Equation (2.82), page 22 of Pradler’s dissertation [5] for obtaining gravitino interactions with ordinary matter fields.
, which is Equation (2.82), page 22 of Pradler’s dissertation [5] for obtaining gravitino interactions with ordinary matter fields.
We can, to first order model the at in the Gravitino-matter field interaction as [5]
 (12)
(12)
This Equation (12) is the potential energy term of Equation (2.82), page 22 of Josef Pradler’s [5] dissertation, and we argue that the physics of the gravitino, as interacting with matter in the electro weak regime, can be to first order, averaged out to be an energy which can be then made equivilent to  of Equation (11). We argue then that effectively, in early universe conditions that we are looking at, then [6],
of Equation (11). We argue then that effectively, in early universe conditions that we are looking at, then [6],
 (13)
(13)
Then, if we do Equation (13) in this spirit, we can then go to what Glinka-Beckwith wrote [6] and look at
 (14)
(14)
Terms such as
 (15)
(15)
vanish from Equation(14).
Ultimately, the analysis of terms as specified in a gravitino-EW “matter” regime would specify the exact particulars as to Equation (12). We will also venture a first order approximate description as to why the mass of the Graviton in the later regime of space time, near the present would be so much smaller than the Gravitino.
5. Conclusion
Via use of the Glinka-Beckwith approximation for the formation of Mass, we have come up with a criteria where the Gravitino interaction with space-time physics in the electro weak, as outlined above, can be construed as either embedded within a larger theory than QM, as suggested by Elze et al. [3], or a corrected Higgs mass formation [2], or something else, which has to be constructed. As outlined by Beckwith [1] there is room to delineate if such a gravitino, using some of the field theoretic construction as given by [5] will be either classically embedded, or something else. The formalism as to massive graviton distortion of early universe space time, as given in [7], and [8] needs to be developed more fully, and we hope we can experimentally test if t’Hoofts supposition about QM [9] is falisifiable experimentally, and analytically, in this early universe setting, as brought up by the author [1].
6. Acknowledgements
This work is supported in part by National Nature Science Foundation of China grant No.110752.
Appendix A
Elze et al. DICE 2010 Summary as to Quantum Mechanics Embedded in a Larger Non Linear Classical Theory
This discussion serves to bring up a Quantum like version of the Liouville equation and to from there to also make sense of the given equation, as of the main text [3]:
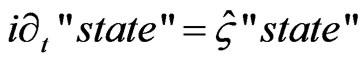 (6)
(6)
To begin with, look at a generic Hamiltonian as given by
 (A1)
(A1)
This Hamiltonian is incorporated in the Lioville equation of motion
 (A2)
(A2)
The upshot if a Fourier transform is taken of Equation (A2) above, and the space like co-ordinates of
 (A3)
(A3)
Equation (A1) then becomes
 (A4)
(A4)
The term put in, namely  which retrieves if we have classical or quantum information, and also, note
which retrieves if we have classical or quantum information, and also, note
 (A5)
(A5)
And
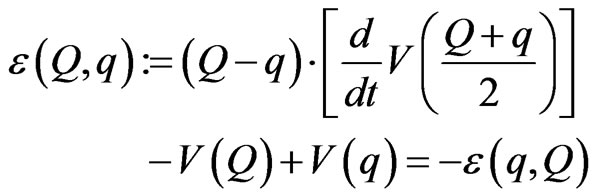 (A6)
(A6)
Then,
 (A7)
(A7)
If so, then one can write
 (A8)
(A8)
I.e. then we have that for the potentials represented by Equation (7), there is an overlap between classical and quantum versions of the Liouville equation as given by the Von Neuman equation as presented by
 (A9)
(A9)
In so many words, we have a QM type situation guaranteed if Equation (A7) holds, whereas we can solve a more general theoretical construction in which there may be what is known as a super action given by
 (A10)
(A10)
We then will be stuck with working with Equation (A4).
When the super action is reduced to, with Equation (A7)
To
 (A11)
(A11)
We recover Equation (A9).
In short, the restrictions on the potential energy, as given by Equation (A7) are essential for the formation of quantum mechanics for exact quantum mechanical Hilbert space operators, whereas more general cases with .
.
Embedd quatum mechanics into the semi classical equation regime, as was specified by Elze and others.
Appendix B
Problems with the Higgs Equation, Lectured Upon in Chongqing University, November 2011
We summarize the main point of Comay’s article [2] in terms of their relationship to the Dirac equation and the question of what is the optimal form of a physics equation most in fidelity to experimental measurements.
The initial points of this borrowing from Comay have already been made in Equation (2) to Equation (5) so we will be discussing the action integral intepretation which Comay made, which was his primary way to differentiate between the faulty mathematics as he saw in the Higgs equation and the Dirac equation. We will reproduce his arguments as to that intepretation in this appendix.
 (B1)
(B1)
Here,  is a Lagrangian density function which is a Lorentz scalar, so then Equation (B1) is a Lorentz scalar.
is a Lagrangian density function which is a Lorentz scalar, so then Equation (B1) is a Lorentz scalar.
The consequences that equation (B1) is a Lorentz scalar lead to several claims by Comay to follow upon and to use.
CLAIM 1:
1) A relativistically consistent quantum theory may be derived from Lagrangian density  which is a Lorentz scalar.
which is a Lorentz scalar.
2) An acceptable dimension for a Lagrangian density is of the form 
3) A wave functional  for both
for both  and
and  cannot define a composite particle if
cannot define a composite particle if  is for a single four dimensional point in space time Sub claim to 3 above, and an effective re statement of 3 is: If
is for a single four dimensional point in space time Sub claim to 3 above, and an effective re statement of 3 is: If  were for a single ( not composite ) particle, then 3*. A:
were for a single ( not composite ) particle, then 3*. A:  needs space time co-ordinates of its center of energy 3*. B: One needs additional co-ordinates for describing internal structure.
needs space time co-ordinates of its center of energy 3*. B: One needs additional co-ordinates for describing internal structure.
We shall then go to the next specific Comay Claim, namely CLAIM 2 Use the following procedure to get consistency of a quantum (massive particle) theory with a classical (massive particle) particle theory, namely by using the following field equation, as given by
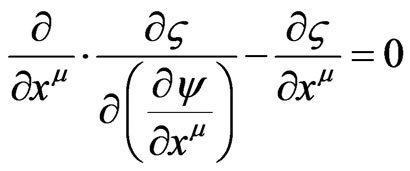 (B2)
(B2)
For energy start off with the equation given by the 2nd order tensor,  , with
, with 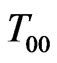 the energy density, and
the energy density, and 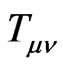 having
having  dimensions, with
dimensions, with
 (B3)
(B3)
Sub set of CLAIM 2. In QM, the Hamiltonian is equal to the total energy, so we can write 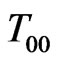 as the Hamiltonian density
as the Hamiltonian density
 (B4)
(B4)
Equation (B4) satisfies the continuity equation as given by
 (B5)
(B5)
Then either of the two happen:
A. Hamiltionian density  may be used to extract Hamiltonian H so that one can write a Hamiltonian
may be used to extract Hamiltonian H so that one can write a Hamiltonian 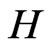 so that then the following happens: Energy E is an eignvalue of
so that then the following happens: Energy E is an eignvalue of 
 (B6)
(B6)
And the De Broglie functions hold as given by
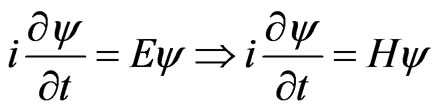 (B7)
(B7)
So then the Hilbert space is formed using all 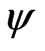 of
of  (completeness of the Hilbert space, using basis from
(completeness of the Hilbert space, using basis from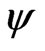 ).
).
OR B. Use expression for density to form inner product for inner product of 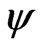 and construct an orthormal baisis set ( often using Gram Schmitz orthoganization) for othnormal basis for corresponding Hilbert space.
and construct an orthormal baisis set ( often using Gram Schmitz orthoganization) for othnormal basis for corresponding Hilbert space.
Then, after B, to then look at a matrix equation given by
 (B8)
(B8)
Form a matrix from Equation (B8), and then diagonalize this matrix to get eignvalues 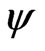 and ENERGY eignvectors .
and ENERGY eignvectors .
ClAIM 3 Proceedures from CLAIM 1 and CLAIM 2, give the same eignvalues and eignvectors, SAME information.
CLAIM 4 The following Equations give almost the same information, one QM, and the other CM (Quantum versus Classical)
 (B9)
(B9)
 (B10)
(B10)
Applications of this formulation. See the Dirac Equation as given by Bjorken And Drell, [10], plus Comay [2].
This example works beautifully. Pion physics, Quark physics and more. There is an excellent match up with experiment.
Next application, Higgs equation, so that
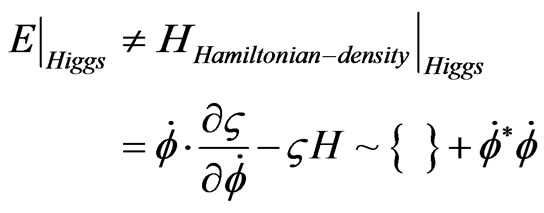 (B11)
(B11)
Here we see then that
 (B12)
(B12)
Specifically, for the Higgs, one has
 (B13)
(B13)
Equation (B13) will then lead to a Higgs potential energy looking like, in simplest form. Where we only know the ratio of .
.
 (B14)
(B14)
And we get a vacuum state given by
 (B15)
(B15)
For the Higgs nucleation of mass, for a Graviton, we have a huge problem, i.e. many undetermined coefficients.
This is similar to what happens with Bjorken’s work [11].
Let  be the Hubble rate of expansion of the cosmos, and set a scale factor as
be the Hubble rate of expansion of the cosmos, and set a scale factor as
 (B17)
(B17)
Here we can re phrase 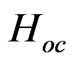 as being the Hubble rate of expansion without torsion added in. Also
as being the Hubble rate of expansion without torsion added in. Also
 (B18)
(B18)
If we go to the Zeldovich relationship
 (B19)
(B19)
Then we get a Lorentz violating “Lagrangian” added on term looking like, if
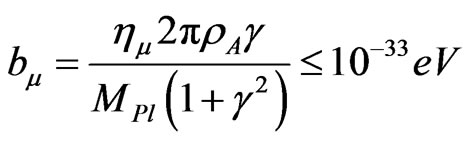 (B20)
(B20)
 (B21)
(B21)
This Equation (B20) is a ten orders too small Lorentz violation term, in the Potential for a Lagrangian, for space-time emergence, but if it were larger, it would be similar in effect to the problem with the Higgs which Comay is outlining. Very close.