1. Introduction
In 1908, Phragmén and Lindelöf ( See, e.g. [1]) showed that if 
is an entire function of order
, then its indicator which is defined as:
has the following property:
If
, and 
is the function of the form
(such functions are called sinusoidal or ρ-trigonometric) which coincides with 
at 
and at
, then for 
we have
This property is called a trigonometric ρ-convexity ([1,2]).
In this article we shall be concerned with real finite functions defined on a finite or infinite interval 
A well known theorem [3] in the theory of ordinary convex functions states that: A necessary and sufficient condition in order that the function 
be convex is that there is at least one line of support for 
at each point 
in 
In Theorem 3.1, we prove this result in case of trigonometrically ρ-convex functions. In Theorem 3.2, we prove the extremum property [4] of convex functions in case of trigonometrically ρ-convex functions. And finally in Theorem 3.3, we show that the average function [5] of a trigonometrically ρ-convex function is also trigonometrically ρ-convex.
2. Definitions and Preliminary Results
In this section we present the basic definitions and results which will be used later , see for example ([1,2], and [6-9]).
Definition 2.1. A function 
is said to be trigonometrically ρ-convex if for any arbitrary closed subinterval 
of 
such that 
, the graph of 
for 
lies nowhere above the ρ-trigonometric function, determined by the equation
where 
and 
are chosen such that 
and 
Equivalently, if for all 
(1)
The trigonometrically ρ-convex functions possess a number of properties analogous to those of convex functions.
For example: If 
is trigonometrically ρ-convex function, then for any 
such that 
the inequality 
holds outside the interval 
Definition 2.2. A function
is said to be supporting function for 
at the point 
if
(2)
That is, if 
and 
agree at 
and the graph of 
does not lie under the support curve.
Remark 2.1. If 
is differentiable trigonometrically ρ-convex function, then the supporting function for 
at the point 
has the form
Proof. The supporting function 
for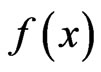 
at the point 
can be described as follows:
where 
such that
and as
Then taking the limit of both sides as 
and from (1), one obtains
Thus, the claim follows.
Theorem 2.1. A trigonometrically ρ-convex function 
has finite right and left derivatives 
at every point 
and 
for all 
Theorem 2.2. Let 
be a two times continuously differentiable function. Then 
is trigonome-trically ρ-convex on 
if and only if 
for all 
Property 2.1. Under the assumptions of Theorem 2.1, the function 
is continuously differentiable on 
with the exception of an at most countable set.
Property 2.2. A necessary and sufficient condition for the function 
to be a trigonometrically ρ-convex in 
is that the function
is non-decreasing in
.
Lemma 2.1. Let 
be a continuous, 
- periodic function, and the derivative 
exists and piecewise continuous function and let 
be a set of discontinuity points for 
If
(3)
and 
where
(4)
Then 
is trigonometrically ρ-convex on
.
Proof. Consider
(5)
Two cases arise, as follows.
Case 1. Suppose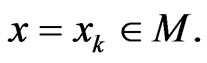 
Using (5), we observe
From (3), we get 
So, the function 
is non-decreasing in 
Case 2. Let 
and
Differentiating both sides of (5) with respect to 
one has
Using (4), one obtains
Thus, 
is non-decreasing function in 
Therefore, from Property 2.2, we conclude that the function 
is trigonometrically ρ-convex on
.
3. Main Results
Theorem 3.1. A function 
is trigonometrically ρ-convex on 
if and only if there exists a supporting function for 
at each point 
in
.
Proof. The necessity is an immediate consequence of F. F. Bonsall [10].
To prove the sufficiency, let 
be an arbitrary point in 
and 
has a supporting function at this point. For convenience, we shall write the supporting function in the follwoing form:
where 
is a fixed real number depends on 
and
.
From Definition 2.2, one has
It follows that,
(6)
For all 
choose any 
such that 
and 
with 
and let 
Applying (6) twice at 
and at 
yields
Multiplying the first inequality by 
the second by 
and adding them, we obtain
Consequently
for all 
which proves that the function 
is trigonometrically ρ-convex on
.
Hence, the theorem follows.
Remark 3.1. For a trigonometrically ρ-convex function
, the constant 
in the above theorem is equal to 
if 
is differentiable at the point 
in
, otherwise, 
Theorem 3.2. Let 
be a trigonometrically ρ-convex function such that 
and let 
be a supporting function for 
at the point 
Then the function
has a minimum value at 
Proof. From Definition 2.2, we have
(7)
and
(8)
and 
can be written in the form
(9)
where 
and 
Using (9), one obtains
Consequently,
(10)
Using (7) at 
the function 
becomes
(11)
But from (8) ,we observe 
for all
.
Now using (10) and (11), it follows that
for all
.
Hence, the minimum value of the function 
occurs at
.
Theorem 3.3. Let 
be a non-negative, 2π- periodic, and trigonometrically ρ-convex function with a continuous second derivative on 
and let 
be a 2π-periodic function defined in 
as follows
(12)
If 
and
(13)
Then, 
is trigonometrically ρ-convex function.
Proof. The proof mainly depends on Lemma 2.1. So, we show that the function 
satisfies all conditions in this lemma.
Suppose that
(14)
It is obvious that, 
First, we study the behavior of the function 
inside the interval
.
It is clear from (12) that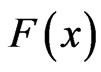 
s is an absolutely continuous function, has a derivative of third order.
But from the periodicity of 
and (13), we get
(15)
Using the following substitution
.
It follows that, 
can be written as
and
.
Consequently,
(16)
Since 
is non-negative, trigonometrically ρ-convex function, and 
then from Theorem 2.2 and (16) it follows that
(17)
Second, we prove that
(18)
From the definition of 
in (14) and the periodicity of 
we observe that 
and
.
Again using (14), we have
(19)
Thus, from (15) and (19), one has
, and
.
Hence, from (13), we infer that
and the inequality in (18) is proved.
Now using (17), (18), and Lemma 2.1, we conclude that 
is trigonometrically ρ-convex function, and the theorem is proved.
4. Acknowledgements
The author wishes to thank the anonymous referees for their fruitful comments and suggestions which improved the original manuscript.