Dynamical Adaptive Particle Swarm Algorithm and Its Application to Optimization of PID Parameters ()
1. Introduction
Particle Swarm Optimization is a kind of simulation group (Swarm) intelligent behavior of the Optimization of the algorithm proposed by Kennedy and Eberhart [1] and others. Its thought source from bird prey on behaveior research. Contrasting PSO with the genetic algorithm and the ant colony algorithm, the PSO method is simple and easy to implement, and it can be adjusted less parameters characteristics. So, it is widely applied in the structural design [2], electromagnetic field [3] task scheduling [4] engineering optimization problems.
In the particle swarm algorithm, the adjusted parameters are the most important part in the inertia weights. In order to find a inertia of weights selection method which can get the best balance between the global search and local search, the researchers have put forward to the linear decrease weights (LDIW) strategy [5], fuzzy inertia weights (FIW) strategy [6], and random inertia weights (RIW) strategy [7], and so on.
In the basic thought of diminishing inertia value guidance, this paper introduces a new adaptive self-adapting inertia, which is based on expectations of survival rate. When the expected survival rate gets smaller, it shows that the optimal particle distance to position is further, at this time, we should make particles into the local search rapidly, the authors shall propose a new dynamic adaptive particle swarm optimization algorithm (DAPSO), and using this algorithm to calculate optimizer in the PID regulator parameters of industrial control system.
This paper is divided into five sections. Section 2 includes preliminaries and related results which will be used in later sections. Section 3 is devoted to introduce dynamic adaptive particle swarm optimization algorithm. In Section 4, we shall use the dynamic adaptive particle swarm optimization algorithm to optimize the PID parameters. Section 5 is the conclusion and working direction in the further.
2. Basic PSO Algorithm and the Related Concept
Particle swarm optimization was firstly proposed in 1995 by Kennedy and Eberhart [1], using the following formula in the particle group of operation:
 (1)
(1)
 (2)
(2)
which i = 1, 2, ···, m, d =1, 2, ···, D; Learning factor c1, c2 is negative constants ;The parameters 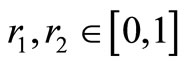 is between the random numbers vid = [–vmax, vmax]; vmax is constant. The i-th particles in a D-dementional vector is xi = (xi1, xi2, ···, xiD), In the space of flight speed is vi and vi = (vi1, vi2, ···, viD); The i-th known so far to search the optimum position is pi = (pi1, pi2, ···, piD), the particle swarm so far to search the optimal position is pg = (pg1, pg2, ···, pgD). In the literature [7], the speed Equation (1) have made the following changes:
is between the random numbers vid = [–vmax, vmax]; vmax is constant. The i-th particles in a D-dementional vector is xi = (xi1, xi2, ···, xiD), In the space of flight speed is vi and vi = (vi1, vi2, ···, viD); The i-th known so far to search the optimum position is pi = (pi1, pi2, ···, piD), the particle swarm so far to search the optimal position is pg = (pg1, pg2, ···, pgD). In the literature [7], the speed Equation (1) have made the following changes:
 (3)
(3)
where w is inertia coefficient,c1, c2 are nonnegative, Equations (1) and (3) are basic PSO iterative formula.
Experimental results show the particle swarm optimization algorithm whether premature convergence or global convergence, particle swarm of particles will appear “together” phenomenon. Therefore, we study the change of the affinity between particles, particle swarm state can be track, the affinity between particles reflect the similarity between the particle, when affinity is large, and the number particles are more similar. Conversely, similar degree is poor. We shall make the parts thought of immune algorithm to fuse the particle swarm optimization algorithm, and give the new definition of affinity and the concept of antibody concentration, the construction method of nonlinear adaptive inertia the weights, and based on this, it improves the dynamic adaptive particle swarm optimization algorithm in [8].
3. Dynamic Adaptive Particle Swarm Optimization Algorithm
Now, we introduce the dynamic adaptive particle swarm optimization algorithm:
DAPSO
Step 1: The particle position and speed of Random initial particle swarm.
Step 2: Make the particles, pb to be the current position, set pg to the best position of particles in initial population.
Step 3: Judg algorithm convergence criteria whether meet, if meet, true to Step 5; or, execute Step 4.
Step 4: To the all particles of particle swarm, execute the following operations:
1) According to the type (1), (2), (3) update the particle’s position and speed;
2) According to the type of above, deduce a dynamic adaptive inertia weights, turn to Step 2.
Step 5: output pg, the algorithm to run is end.
4. Using the Dynamic Adaptive Particle Swarm Optimization Algorithm to Optimize the PID Parameters
4.1. PID Regulator Parameters’ Optimization Problem
In the industrial control system, lots of control objects under the action of step representation the output signal is S form rises curve, right now, can use a second order inertia and delayed model to describe it. Its transfer function is:

In order to make the control object’s output y in disturbance action maintain, we usually use proportion, integral, differential (P, I, D) regulator to form a constant adjustment system.
When the production process is stable, which object characteristics are stable, K, T1, T2 and T3 are basically constant, at this time, PID parameters which are once adjusted would not be charged, but, when the production process is in a constantly changed situation, the reaction conditions such as chemical engineering change, power plant and the change of load, so some object K, T1, T2 and T3 will have a corresponding changed, at this time, if we still keep PID parameters unchanged, it will be difficult to achieve the optimal regulation effect. In the condition of constant fluctuation, because the computer has strong ability of calculation and control on flexibility, we can achieve the adjustment type DDC control. Therefore, using the computer to carry on the PID regulator parameters adjustment and control system has the very strong superiority [9].
Now using a computer to achieve P, I, D adjustment, then we control u and deviation between e to satisfy the

or

Among them, u(n) for the control effect; u(n – 1) for the previous control function; e(n) for the deviation; and e(n – 1) for the previous deviation; and e(n – 2) for again the first deviation.
T is the sampling period, KP is gain coefficient ratio, TI is integral time constant, Td is differential time constant.
Now the task is to search the best: seek the PID three parameters KP, TI, Td, to make the objective function is the smallest It belongs to nonlinear planning in the multivariate function optimization problem, and can not use a mathematical

expression to express the relations between the objective function and variables KP, TI, Td. In this situation, this paper uses the dynamic adaptive particle swarm optimization algorithm and obtains the better results.
4.2. The Results of the Simulation Experiment
If we input the following data:
Variable number N = 3;
the calculation precision E = 0.01;
Compression factor is 0.618; Expansion factor is 1.5.
The parameters of the controlled objects T1 = 0.44 s; T2 = 0.44 s; T3 = 0.12 s;
The total number of print L3 = 30; a given number of control system’s input value R = 10;
PID parameters KP, TI, Td initial value X(1, 0) = 1.5; X(2, 0) = 0.88; X(3, 0) = 0.11.
For DAPSO, the size of the group set to 30, the terminate algebra is 50, set for this d range of 15%, c1, c2 are all 2, a maximum of self-adapting inertia is 0.8, minimum number is 0.2.
The calculated parameters correspond to the control object T1, T2 and T3 is with a given number, the optimal number of PID regulator parameters KP, TI, Td: KP = 1.69764, TI = 0.772662 s, Td = 0.229209 s.
In addition, when KP, TI, Td is the best number, we still obtain all sampling moments of output X1, and deviation quantity X5, as is shown in Table 1.
The system output overshoots is E = 1.42%, the transition process time is TP = 1.1 s.


Table 1. The output results of system simulation.
According to the standard of the engineering design method I system, the system of the output overshoot is E = 4.3%, the transition process time is TP = 1.76 s. Contrast with the results, it shows the parameters which get by using this algorithm are much superior
5. Conclusion and Working Direction
This paper puts forward a dynamic changing the inertia weights of the adaptive particle swarm algorithm (DAPSO), and using the algorithm to optimize the PID parameters, the simulation results show that this method, contrasted with a relatively routine of the simplex method, has a lot of advantages, such as the fast speed, accuracy, the optimal speed, accurate, to improve the dynamic system, etc. Having the prospect of the good application and the further research, however, for the function, which is very complex and exists many local optimizations near the optimal solution, the results are not very ideal. Therefore, further work direction is: expanding the scope of the algorithm testing, seeking the cooperate ways between particles, and to a certain extent, analysis, the convergence and robustness of PAPSO.
6. Acknowledgements
This work is supported by Natural science foundation of the State Ethnic Affairs Commission of PRC (No. 10BF07); Zizhu Natural Science Foundation of Beifang University for Nationalities (No. 2011ZQY024). Ministry of Education Science and technology key projects (No. 212204); Natural Science Foundation for the Youth (No. 10901004).