Boundary Control Problem of Infinite Order Distributed Hyperbolic Systems Involving Time Lags ()
1. Introduction
Distributed parameters systems with delays can be used to describe many phenomena in the real world. As is well known, heat conduction, properties of elastic-plastic material, fluid dynamics, diffusion-reaction processes, the transmission of the signals at a certain distance by using electric long lines, etc., all lie within this area. The object that we are studying (temperature, displacement, concentration, velocity, etc.) is usually referred to as the state.
The optimal control problems of second order distributed parabolic and hyperbolic systems involving time lags appearing in the boundary condition have been widely discussed in many papers and monographs. A fundamental study of such problems is given by [1] and was next developed by [2] and [3]. It was also intensively investigated by [4-14] and [15,16] in which linear quadratic problem for parabolic and hyperbolic systems with time delays given in the different form (constant time delays, time-varying delays, time delays given in the integral form, etc.) were presented.
In this paper, we consider the optimal control for infinite order hyperbolic systems and for (n × n) infinite order hyperbolic systems involving constant time lags appearing in both in the state equation and in the boundary condition. Such an infinite order hyperbolic system can be treated as a generalization of the mathematical model for a plasma control process.
The quadratic performance functional defined over a fixed time horizon are taken and some constraints are imposed on the boundary control. Following a line of the Lions scheme, necessary and sufficient optimality conditions for the Neumann problem applied to the above system were derived. The optimal control is characterized by the adjoint equations.
This paper is organized as follows. In Section 1, we introduce spaces of functions of infinite order. In Section 2, we formulate the mixed Neumann problem for infinite order hyperbolic systems involving constant time lags. In Section 3, the boundary optimal control problem for this case is formulated, then we give the necessary and sufficient conditions for the control to be an optimal. In Section 4, we concluded and generalized our results.
2. Sobolev Spaces with Infinite Order
The object of this section is to give the definition of some function spaces of infinite order, and the chains of the constructed spaces which will be used later.
Let 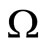 be a bounded opesn set of
be a bounded opesn set of 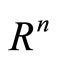 with a smooth boundary
with a smooth boundary , which is a
, which is a  -manifold of dimension
-manifold of dimension . Locally,
. Locally,  is totally on one side of
is totally on one side of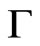 . We define the infinite order Sobolev space
. We define the infinite order Sobolev space  of infinite order of periodic functions
of infinite order of periodic functions 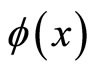 defined on
defined on  [17-19] as follows:
[17-19] as follows:

where  is the space of infinite differentiable functions,
is the space of infinite differentiable functions,  is a numerical sequence and
is a numerical sequence and  is the canonical norm in the space
is the canonical norm in the space , and
, and
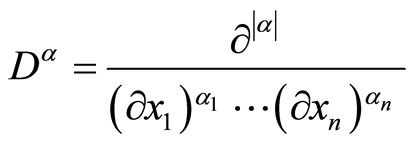
 being a multi-index for differentiation,
being a multi-index for differentiation, .
.
The space  is defined as the formal conjugate space to the space
is defined as the formal conjugate space to the space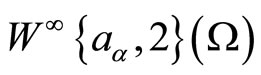 , namely:
, namely:

where  and
and 
The duality pairing of the spaces  and
and  is postulated by the formula
is postulated by the formula

where

From above,  is everywhere dense in
is everywhere dense in  with topological inclusions and
with topological inclusions and  denotes the topological dual space with respect to
denotes the topological dual space with respect to , so we have the following chain of inclusions:
, so we have the following chain of inclusions:

We now introduce  which we shall denoted by
which we shall denoted by , where
, where  denotes the space of measurable functions
denotes the space of measurable functions  such that
such that

endowed with the scalar product
 , L2(Q) is a Hilbert space.
, L2(Q) is a Hilbert space.
In the same manner we define the spaces
 , and
, and as its formal conjugate.
as its formal conjugate.
Also, we have the following chain of inclusions:

The construction of the Cartesian product of n-times to the above Hilbert spaces can be construct, for example
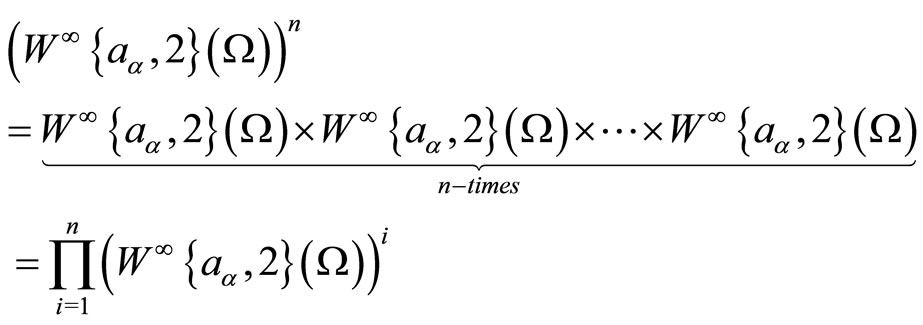
with norm defined by:
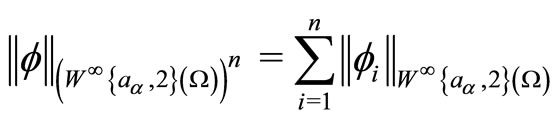
where 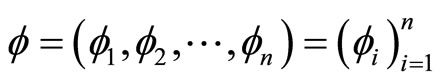 is a vector function and
is a vector function and
 .
.
Finally, we have the following chain of inclusions:

where  are the dual spaces of
are the dual spaces of . The spaces considered in this paper are assumed to be real.
. The spaces considered in this paper are assumed to be real.
3. Mixed Neumann Problem for Infinite Order Hyperbolic System Involving Time Lags
The object of this section is to formulate the following mixed initial boundary value Neumann problem for infinite order hyperbolic system involving time lags which defines the state of the system model.
 (1)
(1)
 (2)
(2)
 (3)
(3)
 (4)
(4)
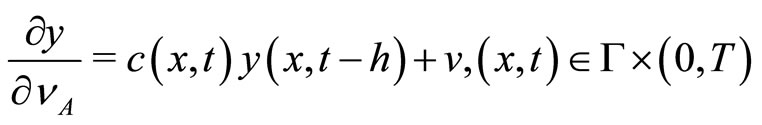 (5)
(5)
 (6)
(6)
where  has the same properties as in Section 1. We have
has the same properties as in Section 1. We have

• 
• T is a specified positive number representing a finite time horizon;
• h is a specific positive number representing a time lag;
•  are given real
are given real  functions defined on
functions defined on ,
,  respectively;
respectively;
• y is a function defined on Q such that  ;
;
• u, v are functions defined on Q and  such that
such that  and
and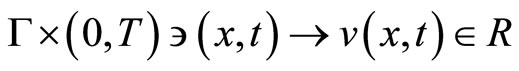 ;
;
•  are initial functions defined on
are initial functions defined on  such that
such that
 .
.
 .
.
The hyperbolic operator 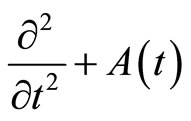 in the state Equation (1) is an infinite order hyperbolic operator and
in the state Equation (1) is an infinite order hyperbolic operator and  [19] is given by:
[19] is given by:

and
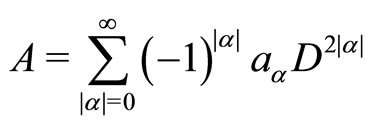
is an infinite order self-adjoint elliptic partial differential operator maps  onto
onto .
.
For this operator we define the bilinear form as follows:
Definition 2.1. For each , we define a family of bilinear forms on
, we define a family of bilinear forms on  by:
by:

where  maps
maps  onto
onto  and takes the above form. Then
and takes the above form. Then

Lemma 2.1. The bilinear form  is coercive on
is coercive on  that is
that is
 (7)
(7)
Proof. It is well known that the ellipticity of 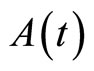 is sufficient for the coerciveness of
is sufficient for the coerciveness of  on
on  .
.

Then

Also we have:
 (8)
(8)
Equations (1)-(6) constitute a Neumann problem. Then the left-hand side of the boundary condition (5) may be written in the following form:
 (9)
(9)
where  is a normal derivative at
is a normal derivative at , directed towards the exterior of
, directed towards the exterior of , and
, and 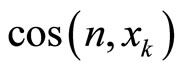 is the
is the  direction cosine of n, with n being the normal at
direction cosine of n, with n being the normal at  exterior to
exterior to .
.
Then (5) can be written as:
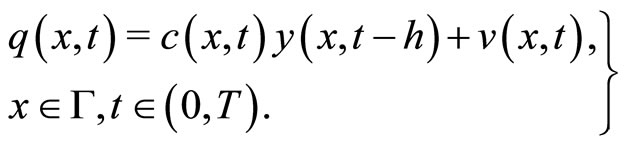 (10)
(10)
We shall formulate sufficient conditions for the existence of a unique solution of the mixed boundary value problem (1)-(6) for the case where the boundary control . For this purpose we introduce the Sobolev space
. For this purpose we introduce the Sobolev space  [20] (p. 6) defined by:
[20] (p. 6) defined by:
 (11)
(11)
which is a Hilbert space normed by
 (12)
(12)
where the space 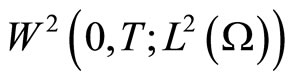 denotes the Sobolev space of second order of functions defined on
denotes the Sobolev space of second order of functions defined on 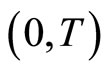 and taking values in
and taking values in  [20] .
[20] .
The existence of a unique solution for the mixed initial-boundary value problem (1)-(6) on the cylinder Q can be proved using a constructive method, i.e., solving at first Equations (1)-(6) on the sub-cylinder Q1 and in turn on Q2 etc., until the procedure covers the whole cylinder Q. In this way, the solution in the previous step determines the next one.
For simplicity, we introduce the following notation:

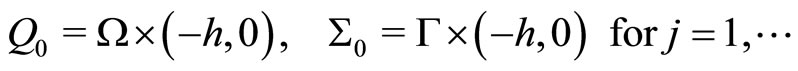
Using Theorem 6.1 of [20] (Vol. 2, p. 33), then the following result holds.
Theorem 2.1. Let y0,  ,
,  ,
, 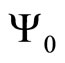 , v and u be given with
, v and u be given with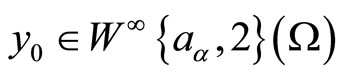 ,
,  ,
,
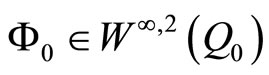 ,
,  ,
,  and
and
 and the following compatibility relations:
and the following compatibility relations:
 (13)
(13)
 (14)
(14)
Then, there exists a unique solution  for the mixed initial-boundary value problem (1)-(6). Moreover,
for the mixed initial-boundary value problem (1)-(6). Moreover, 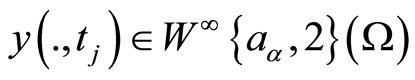
 , for
, for .
.
4. Problem Formulation and Optimization Theorems
Now, we formulate the optimal control problem for (1)- (6) in the context of the Theorem 2.1, that is .
.
Let us denote by  the space of controls. The time horizon
the space of controls. The time horizon  is fixed in our problem.
is fixed in our problem.
The performance functional is given by:
 (15)
(15)
where , and
, and 
 is a given element in
is a given element in ; N is a positive linear operator on
; N is a positive linear operator on  into
into .
.
Control constraints: We define the set of admissible controls  such that
such that
 (16)
(16)
Let  denote the solution of the mixed initialboundary value problem (1)-(6) at
denote the solution of the mixed initialboundary value problem (1)-(6) at  corresponding to a given control
corresponding to a given control . We note from Theorem 2.1 that for any
. We note from Theorem 2.1 that for any  the performance functional (15) is well-defined since
the performance functional (15) is well-defined since .
.
Making use of the Loins’s scheme we shall derive the necessary and sufficient conditions of optimality for the optimization problem (1)-(6), (15), (16). The solving of the formulated optimal control problem is equivalent to seeking a  such that
such that
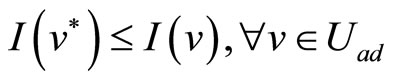
From the Lion’s scheme [21] (Theorem 1.3 of, p. 10), it follows that for 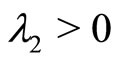 a unique optimal control
a unique optimal control  exists. Moreover,
exists. Moreover,  is characterized by the following condition:
is characterized by the following condition:
 (17)
(17)
For the performance functional of form (15) the relation (17) can be expressed as
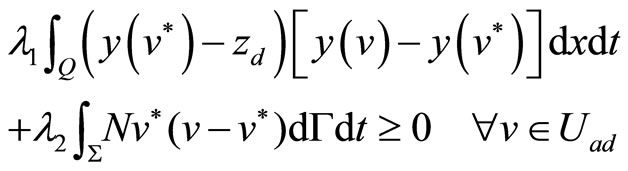 (18)
(18)
In order to simplify (18), we introduce the adjoint equation, and for every , we define the adjoint variable
, we define the adjoint variable  as the solution of the equations:
as the solution of the equations:
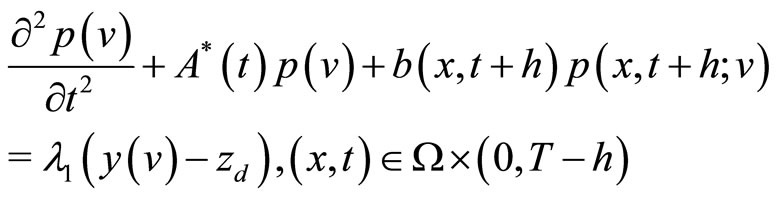 (19)
(19)
 (20)
(20)
 (21)
(21)
 (22)
(22)
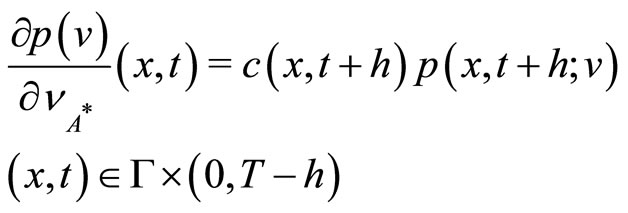 (23)
(23)
 (24)
(24)
where 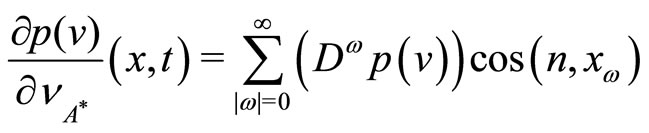
 (25)
(25)
As in the above section with change of variables, i.e. with reversed sense of time. i.e.,  , for given
, for given  and any
and any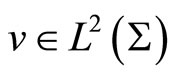 , there exists a unique solution
, there exists a unique solution 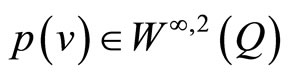 for problem (19)-(24).
for problem (19)-(24).
The existence of a unique solution for the problem (19)-(24) on the cylinder Q can be proved using a constructive method. It is easy to notice that for given 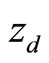 and v, the problem (19)-(24) can be solved backwards in time starting from
and v, the problem (19)-(24) can be solved backwards in time starting from , i.e. first solving (19)-(24) on the sub-cylinder
, i.e. first solving (19)-(24) on the sub-cylinder  and in turn on
and in turn on , etc. until the procedure covers the whole cylinder Q. For this purpose, we may apply Theorem 2.1 (with an obvious change of variables). Hence, using Theorem 2.1, the following result can be proved.
, etc. until the procedure covers the whole cylinder Q. For this purpose, we may apply Theorem 2.1 (with an obvious change of variables). Hence, using Theorem 2.1, the following result can be proved.
Lemma 3.1. Let the hypothesis of Theorem 2.1 be satisfied. Then for given  and any
and any , there exists a unique solution
, there exists a unique solution  for the adjoint problem (19)-(24).
for the adjoint problem (19)-(24).
We simplify (18) using the adjoint equation (19)-(24). For this purpose denoting by 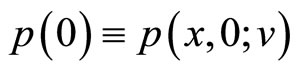 and
and 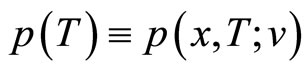 respectively, setting
respectively, setting 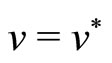 in (19)- (24), multiplying both sides of (19), (20) by y(v) – y(v*), then integrating over
in (19)- (24), multiplying both sides of (19), (20) by y(v) – y(v*), then integrating over  and
and  respectively and then adding both sides of (19), (20), we get
respectively and then adding both sides of (19), (20), we get
 (26)
(26)
Using the Equation (1), the second integral on the right-hand side of (26) can be written as
 (27)
(27)
Using Green’s formula, the third integral on the righthand side of (26) can be written as
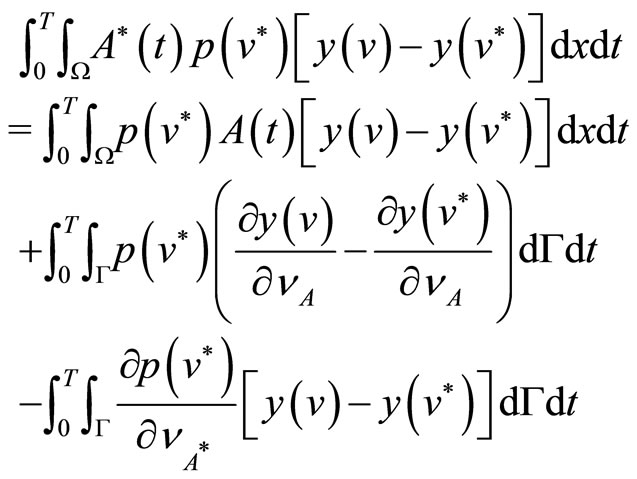 (28)
(28)
Using the boundary condition (5), one can transform the second integral on the right-hand side of (28) into the form:
 (29)
(29)
The last component in (28) can be rewritten as
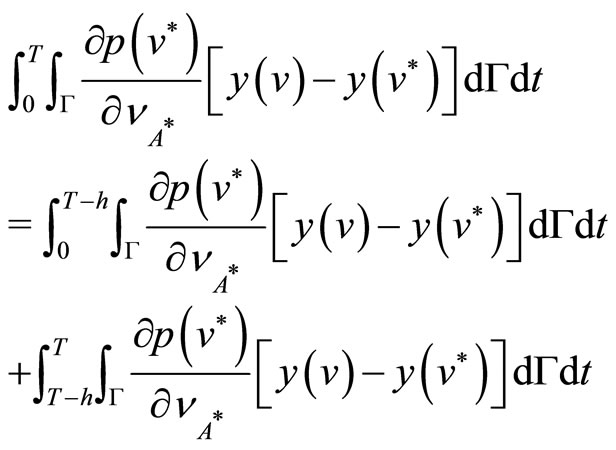 (30)
(30)
Substituting (29) and (30) into (28), and then (27), (28) into (26), we obtain
 (31)
(31)
Substituting (31) into (18) gives
 (32)
(32)
The foregoing result is now summarized.
Theorem 3.1. For the problem (1)-(6), with the performance functional (15) with  and
and  and with conditions (16), there exists a unique optimal control
and with conditions (16), there exists a unique optimal control  which satisfies the maximum condition (32).
which satisfies the maximum condition (32).
Mathematical Examples
Example 3.1. Consider now the particular case where 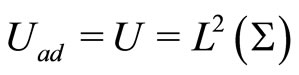 (no constraints case). Thus the maximum condition (32) is satisfied when
(no constraints case). Thus the maximum condition (32) is satisfied when

If N is the identity operator on , then from the Lemma 3.1 follows that
, then from the Lemma 3.1 follows that .
.
Example 3.2. We can also consider an analogous optimal control problem where the performance functional is given by:
 (33)
(33)
where .
.
From Theorem 2.1 and the Trace Theorem [20] (Vol. 2, p. 9), for each , there exists a unique solution
, there exists a unique solution  with
with . Thus,
. Thus,  is well defined. Then, the optimal control
is well defined. Then, the optimal control  is characterized by:
is characterized by:
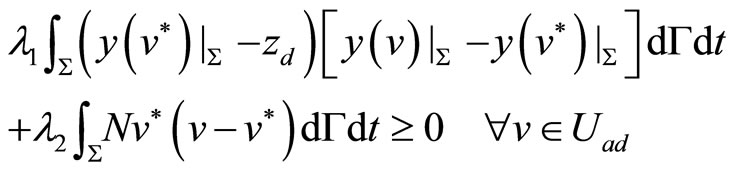 (34)
(34)
We define the adjoint variable 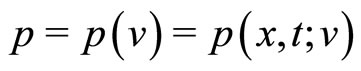 as the solution of the equations:
as the solution of the equations:
 (35)
(35)
 (36)
(36)
 (37)
(37)
 (38)
(38)
 (39)
(39)
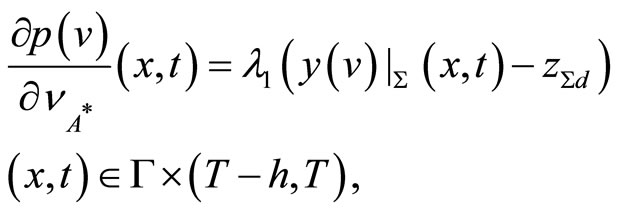 (40)
(40)
As in the above section, we have the following result.
Lemma 3.2. Let the hypothesis of Theorem 2.1 be satisfied. Then, for given  and any
and any  , there exists a unique solution
, there exists a unique solution
 to the adjoint problem (35)-(40).
to the adjoint problem (35)-(40).
Using the adjoint Equations (35)-(40) in this case, the condition (34) can also be written in the following form
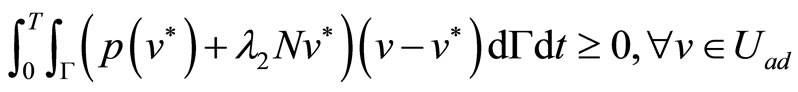 (41)
(41)
The following result is now summarized.
Theorem 3.2. For the problem (1)-(6) with the performance function (33) with  and
and , and with constraint (16), and with adjoint Equations (35)-(40), there exists a unique optimal control
, and with constraint (16), and with adjoint Equations (35)-(40), there exists a unique optimal control  which satisfies the maximum condition (41).
which satisfies the maximum condition (41).
Example 3.3. Case: . We can also consider an analogous optimal control problem where the performance functional is given by:
. We can also consider an analogous optimal control problem where the performance functional is given by:
 (42)
(42)
where .
.
From Theorem 2.1 and the Trace Theorem [20] (Vol. 2, p. 9), for each , there exists a unique solution
, there exists a unique solution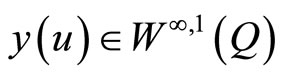 . Thus, I is well defined. Then, the optimal control
. Thus, I is well defined. Then, the optimal control 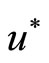 is characterized by
is characterized by
 (43)
(43)
We define the adjoint variable  as the solution of the equations:
as the solution of the equations:
 (44)
(44)
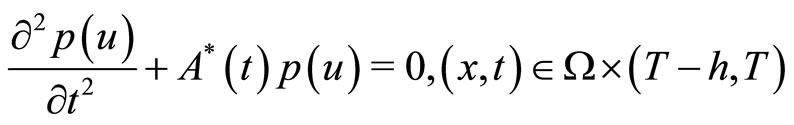 (45)
(45)
 (46)
(46)
 (47)
(47)
 (48)
(48)
 (49)
(49)
As in the above section, we have the following result.
Lemma 3.3. Let the hypothesis of Theorem 2.1 be satisfied. Then, for given  and any
and any , there exists a unique solution
, there exists a unique solution  to the adjoint problem (44)-(49).
to the adjoint problem (44)-(49).
Using the adjoint equations (44)-(49) in this case, the condition (43) can also be written in the following form:
 (50)
(50)
The following result is now summarized.
Theorem 3.3. For the problem (1)-(6), (44)-(49), (16) with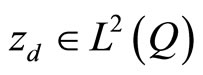 ,
,  , there exists a unique optimal control
, there exists a unique optimal control 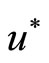 which satisfies the maximum condition (50).
which satisfies the maximum condition (50).
5. Generalization
The optimal control problems presented her can be extended to certain different two cases. Case 1: Optimal control for  coupled infinite order hyperbolic systems involving constant time lags. Case 2: Optimal control for
coupled infinite order hyperbolic systems involving constant time lags. Case 2: Optimal control for  coupled infinite order hyperbolic systems involving constant time lags. Such extension can be applied to solving many control problems in mechanical engineering.
coupled infinite order hyperbolic systems involving constant time lags. Such extension can be applied to solving many control problems in mechanical engineering.
Case 1: Optimal control for 2 × 2 coupled infinite order hyperbolic systems involving constant time lags.
We will extend the discussions to study the optimal control for  coupled infinite order hyperbolic systems involving constant time lags. We consider the case where
coupled infinite order hyperbolic systems involving constant time lags. We consider the case where , the performance functional is given by:
, the performance functional is given by:
 (51)
(51)
where .
.
The following results can now be proved.
Theorem 4.1. Let ,
,  ,
,  ,
,  ,
,  and
and  be given with
be given with
 ,
,
 ,
,
 ,
,
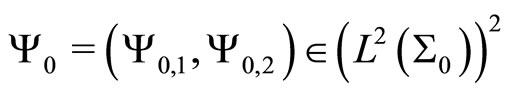 ,
,

and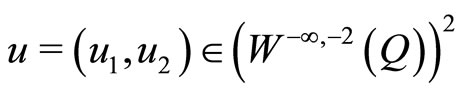 .
.
Then, there exists a unique solution
 for the following mixed initial-boundary value problem:
for the following mixed initial-boundary value problem:
 (52)
(52)
 (53)
(53)
 (54)
(54)
 (55)
(55)
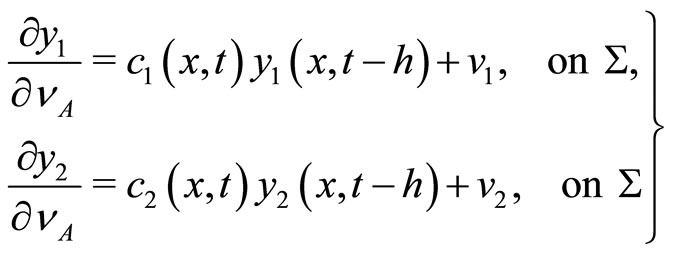 (56)
(56)
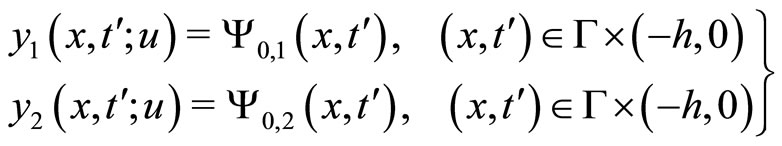 (57)
(57)
where



Lemma 4.1. Let the hypothesis of Theorem 4.1 be satisfied. Then for given  and any
and any , there exists a unique solution
, there exists a unique solution  for the adjoint problem:
for the adjoint problem:
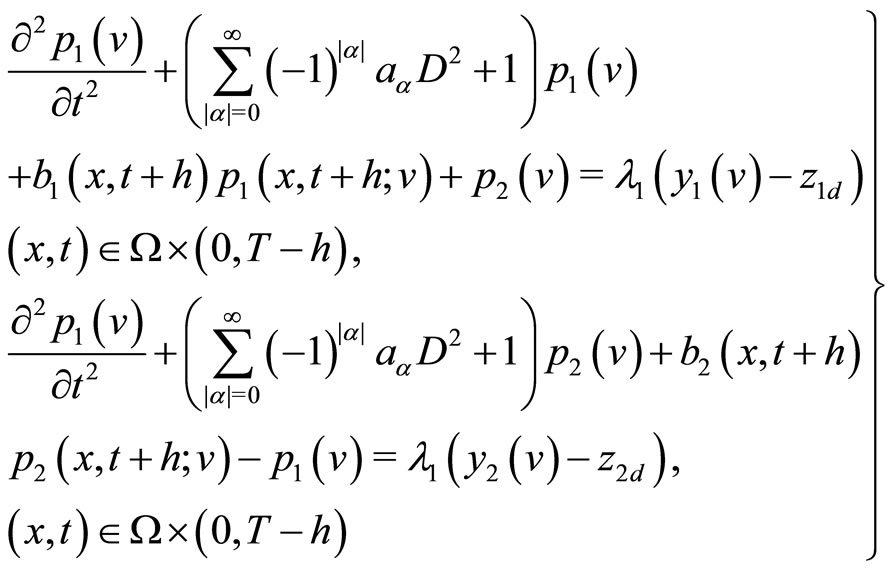 (58)
(58)
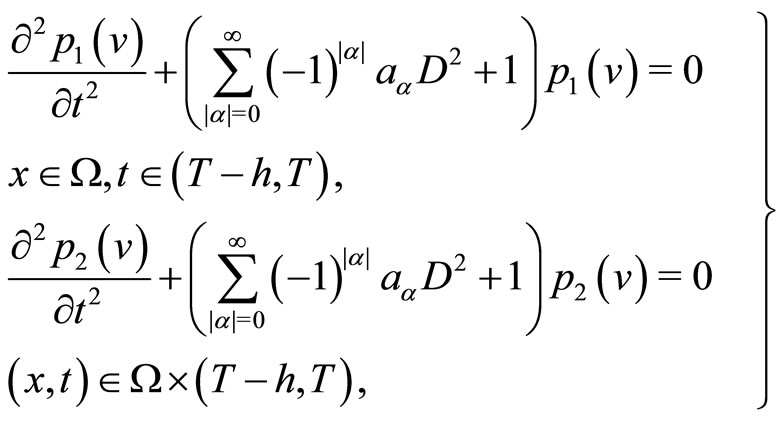 (59)
(59)
 (60)
(60)
 (61)
(61)
 (62)
(62)
 (63)
(63)
Theorem 4.2. The optimal control
 is characterized by the following maximum condition
is characterized by the following maximum condition
 (64)
(64)
where  is the adjoint state.
is the adjoint state.
The foregoing result is now summarized.
Theorem 4.3. For the problem (52)-(57) with the performance function (51) with
 and
and , and with constraint:
, and with constraint: 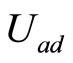 is closed, convex subset of
is closed, convex subset of , and with adjoint equations (58)-(63), then there exists a unique optimal control
, and with adjoint equations (58)-(63), then there exists a unique optimal control

which satisfies the maximum condition (64).
Case 2: Optimal control for n × n coupled infinite order hyperbolic systems involving constant time lags.
We will extend the discussion to n × n coupled infinite order hyperbolic systems involving constant time lags. We consider the case where
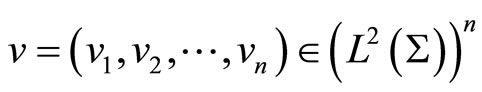 , the performance functional is given by (El-Saify, 2005; 2006):
, the performance functional is given by (El-Saify, 2005; 2006):
 (65)
(65)
where .
.
The following results can now be proved.
Theorem 4.4. Let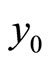 ,
, 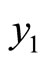 ,
, 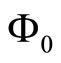 ,
,  ,
,  and
and  be given with
be given with
 ,
,
 ,
,
 ,
,
 ,
,

and .
.
Then, there exists a unique solution
 for the following mixed initial-boundary value problem:
for the following mixed initial-boundary value problem:  we have
we have
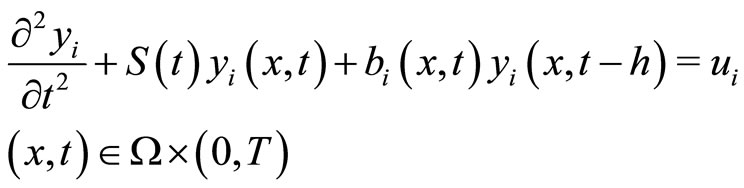 (66)
(66)
 (67)
(67)
 (68)
(68)
 (69)
(69)
 (70)
(70)
 (71)
(71)
where


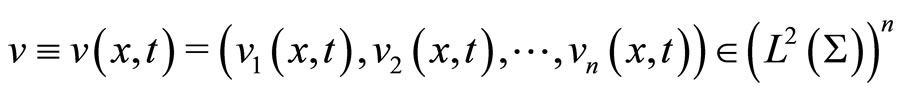
 are given real
are given real  functions defined on
functions defined on , respectively, h is a time lags,
, respectively, h is a time lags,
 are initial functions defined on
are initial functions defined on  respectively.
respectively.
The operator  is an
is an  matrix takes the form [22-25] (El-Saify & Bahaa 2000; 2001; 2002; 2003).
matrix takes the form [22-25] (El-Saify & Bahaa 2000; 2001; 2002; 2003).

That is
 (72)
(72)
where

Lemma 4.2. Let the hypothesis of Theorem 4.4 be satisfied. Then for given
 and any
and any
 , there exists a unique solution
, there exists a unique solution

for the adjoint problem: , we have
, we have
 (73)
(73)
 (74)
(74)
 (75)
(75)
 (76)
(76)
 (77)
(77)
 (78)
(78)
Theorem 4.5. The optimal control
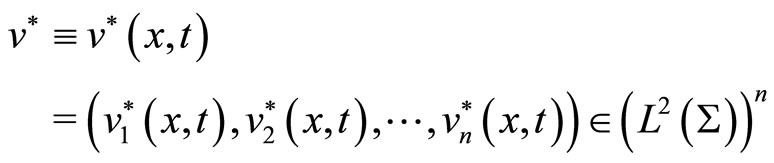
is characterized by the following maximum condition
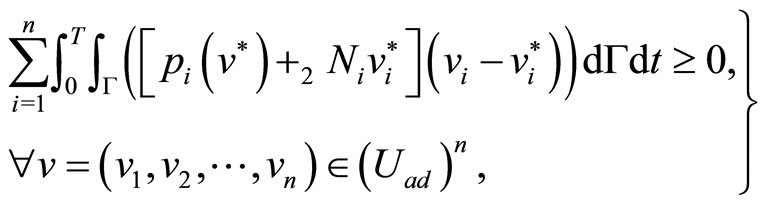 (79)
(79)
where

is the adjoint state.
The foregoing result is now summarized.
Theorem 4.6. For the problem (66)-(71) with the performance function (65) with
 and
and , and with constraint:
, and with constraint:  is closed, convex subset of
is closed, convex subset of , and with adjoint Equations (73)-(78), then there exists a unique optimal control
, and with adjoint Equations (73)-(78), then there exists a unique optimal control

which satisfies the maximum condition (79).
In the case of performance functionals (15, 33, 42, 51 and 65) with  and
and , the optimal control problem reduces to minimization of the functional on a closed and convex subset in a Hilbert space. Then, the optimization problem is equivalent to a quadratic programming one, which can be solved by the use of the well-known Gilbert algorithm.
, the optimal control problem reduces to minimization of the functional on a closed and convex subset in a Hilbert space. Then, the optimization problem is equivalent to a quadratic programming one, which can be solved by the use of the well-known Gilbert algorithm.
6. Conclusions
The optimization problem presented in the paper constitutes a generalization of the optimal boundary control problem of a second order hyperbolic systems involving constant time lags appearing in the boundary condition have been considered in [4-16,22].
In this paper, we have considered the boundary control problem for infinite order hyperbolic system and also for  infinite order hyperbolic systems involving constat time lags appearing both in the state equations and in the Neumann boundary conditions. We can also consider the boundary optimal control problem for
infinite order hyperbolic systems involving constat time lags appearing both in the state equations and in the Neumann boundary conditions. We can also consider the boundary optimal control problem for 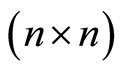 infinite order parabolic or hyperbolic systems with timevarying delays appearing in the state equations and in the Neumann or Dirichlet boundary conditions. We can also consider the boundary optimal control problem for
infinite order parabolic or hyperbolic systems with timevarying delays appearing in the state equations and in the Neumann or Dirichlet boundary conditions. We can also consider the boundary optimal control problem for  infinite order hyperbolic systems with timevarying delays appearing in the integral form with
infinite order hyperbolic systems with timevarying delays appearing in the integral form with  or
or  both in the state equations and in the Neumann or Dirichlet boundary conditions.
both in the state equations and in the Neumann or Dirichlet boundary conditions.
Also it is evident that by modifying:
• The boundary conditions, (Dirichlet, Neumann, mixed, etc.);
• The nature of the control (distributed, boundary, etc.);
• The nature of the observation (distributed, boundary, etc.);
• The initial differential system;
• The time delays (constant time delays, time-varying delays, multiple time-varying delays, time delays given in the integral form, etc.);
• The number of variables (finite number of variables, infinite number of variables systems, etc.);
• The type of equation (elliptic, parabolic, hyperbolic, etc.);
• The order of equation (second order, Schrödinger, infinite order, etc.);
• The type of control (optimal control problem, timeoptimal control problem, etc.), an infinity of variations on the above problem are possible to study with the help of [21] and Dubovitskii-Milyutin formalisms [23-32]. Those problems need further investigations and form tasks for future research. These ideas mentioned above will be developed in forthcoming papers.