1. Introduction
The problem of how to geometrical presentation of the theory of the electron and include it in the scheme of the general relativity theory is far from being solved. The expression for the co-variant derivative obtained in [1] from intuitively consideration, with some interpretation corrections introduced in [2], is the generally accepted formula now. Cartan [3] has showed, however, that finitedimensional representation of a complete linear group of coordinate transformations does not exist. Moreover, the set of Dirac spinors preserves the structure of the linear vector space, but does not preserve the ring structure since defining the composition operation involves some complications. Thus allowed states are depleted inasmuch as wave function behavior under the parallel translation cannot be calculated and appropriately interpreted, and, besides that, the states of the particle ensemble cannot be determined. As early as 1878 G. Frobenius [4] to prove a theorem, that exist only one associative algebra with partition on the field of real number-real number, complex number and Clifford number. The algebra, which use the Clifford number possesses ring structure [5] since it is a vector space over the field of real numbers and hence makes an additive group whose low of elements composition is distributive rather than commutative with respect to addition. This ring has ideals which may be obtained by multiplying the separated element on the right or on the left by ring elements [5]. The ideals resulting from this procedure are just the Dirac spinors of the standard approach. Now, the application of the conventional approch by spinor representation in a Hilbert space is well-known. However attempt to discus the Dirac theory from Clifford algebra itself have been judged to have achieved limited success. Thus the representation of the Clifford algebra by the Clifford number contains more information on particle properties than spinor representations. We known, that the Clifford algebra can be extended to include relativity and plays essential role in the Dirac theory of relativistic electron [6,7].
As was shown early [8-12] covered all the standard features of quantum mechanics. Clifford algebra gives [13] an unifying framework of physical knowledge here including relativity, electromagnetism and other physical matter. When we introduce a Clifford rough scheme of quantum mechanics, as note in [10], we cannot ignore the emerging salient feature of this formulation. It is that in this case we obtain a quantum mechanical theoretical framework invoking only an algebraic structure that does not contain any further specific requirement. It possible to show [8-12], that the Clifford algebraic formalism are completely equivalent to the conventional approach to quantum mechanics. This open up the possibility of a different interpretation an explanation of quantum phenomena in term of a non-commutative geometry and predict the new experiment for determination geometrical presentation of wave function for elementary particle. The mean idea this article are in presentation the particle wave function by a geometric entity, i.e., Clifford number, with the translation rules possessing the structure of Dirac equation for any manifold. A solution of this equation can obtain in terms of geometric treatment. The novel experiments of geometrical nature of wave function determination can be proposed.
2. Wave Function as Geometric Entity
We employ the mean idea of correspondence between the spinor matrices and the elements of an exterior algebra and thus define the space of states in terms of a space of representations of a space-time Clifford algebra. The construction of such algebra [5,7] requires imposing a vector space  over the field of real numbers, and the quadratic form which associated with scalar product. Can introduce the notion of p-vectors i.e. the product of p vectors from
over the field of real numbers, and the quadratic form which associated with scalar product. Can introduce the notion of p-vectors i.e. the product of p vectors from , which geometrically sets the oriented volume constructed upon these vectors. Each p-vector has
, which geometrically sets the oriented volume constructed upon these vectors. Each p-vector has  components and is an element of space of
components and is an element of space of  dimensions and each element, made up by a product of an arbitrary set of p-vectors is an element of vector space with the dimensions
dimensions and each element, made up by a product of an arbitrary set of p-vectors is an element of vector space with the dimensions 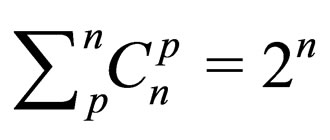 which in itself is a direct sum of its subspaces. Clifford algebra can be constructed for the elements of such space, which makes possible a single approach to the examination of the internal product of any vector associated with quadratic form, and the external product that the ring structure. An arbitrary basis, similar to the vector basis, can be introduce in any point of the space, allowing us to construct an induced vector space with geometrical characteristics of different tensor subspaces. In the case finite dimensionality, the space of function is isomorphic to the space itself. Thus, we can define a single general characteristic in each point of the manifold, regarding it as the direct sum of all possible forms as elements of vector space. The direct sum of such tensor representations can be attributed with the Clifford algebra structure by means of the direct product [5]. The final dimensionality of the algebra is determined by the number of basis vectors, provides the ring structure and is responsible for the existence of an exact matrix representation. Moreover, the space of functional is isomorphic to this very linear space, and the algebra of outer products is isomorphic to the algebra of the outer product of these very vectors.
which in itself is a direct sum of its subspaces. Clifford algebra can be constructed for the elements of such space, which makes possible a single approach to the examination of the internal product of any vector associated with quadratic form, and the external product that the ring structure. An arbitrary basis, similar to the vector basis, can be introduce in any point of the space, allowing us to construct an induced vector space with geometrical characteristics of different tensor subspaces. In the case finite dimensionality, the space of function is isomorphic to the space itself. Thus, we can define a single general characteristic in each point of the manifold, regarding it as the direct sum of all possible forms as elements of vector space. The direct sum of such tensor representations can be attributed with the Clifford algebra structure by means of the direct product [5]. The final dimensionality of the algebra is determined by the number of basis vectors, provides the ring structure and is responsible for the existence of an exact matrix representation. Moreover, the space of functional is isomorphic to this very linear space, and the algebra of outer products is isomorphic to the algebra of the outer product of these very vectors.
In the case of space-time in the special theory of relativity, Clifford algebra is algebra constructed by the Dirac matrix  which is associated with unit vectors. The linear combination product of this matrix has all the properties of the structure of Clifford algebra with three complex units because one time matrix
which is associated with unit vectors. The linear combination product of this matrix has all the properties of the structure of Clifford algebra with three complex units because one time matrix  and three space matrix
and three space matrix . Therefore, we can reproduce any element belonging to the induced vector space in the form of direct sum all possible tensor presentation. The existence of a unique set of linear independent forms defined at an arbitrary point of the space suggests that the nature of the forms translated over the manifold is similar to the nature of forms which characterize it [13]. This may be also determined by the similar form of the geometric entities as functions of elements of the induced space. Making use of this basis, we consider the realization of the different function in the ordinary Euclidean space. In this case the different function may be written in terms of a direct sum of a scalar, a vector, a bi-vector, a three-vector, and a pseudo-scalar,
. Therefore, we can reproduce any element belonging to the induced vector space in the form of direct sum all possible tensor presentation. The existence of a unique set of linear independent forms defined at an arbitrary point of the space suggests that the nature of the forms translated over the manifold is similar to the nature of forms which characterize it [13]. This may be also determined by the similar form of the geometric entities as functions of elements of the induced space. Making use of this basis, we consider the realization of the different function in the ordinary Euclidean space. In this case the different function may be written in terms of a direct sum of a scalar, a vector, a bi-vector, a three-vector, and a pseudo-scalar,
 that is given by
that is given by
 (1)
(1)
with the reverse order of composition, we have

and having changed the direction of each basis vector, we obtain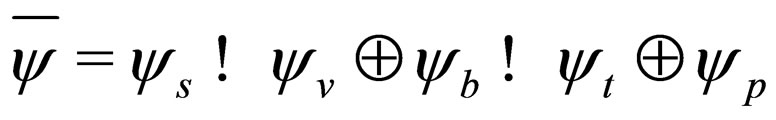 . It is symmetry element for Clifford number. If introduce the notice
. It is symmetry element for Clifford number. If introduce the notice  (complex number we will note as
(complex number we will note as ), can introduce the once one symmetry element as multiplication by i that present as
), can introduce the once one symmetry element as multiplication by i that present as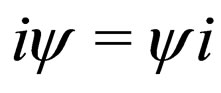 . After introducing symmetry element should be present mathematical operation on the field of Clifford number. The direct sum of tensor subspaces can be given a ring structure with the help of direct tensor product in the following symbolic notation:
. After introducing symmetry element should be present mathematical operation on the field of Clifford number. The direct sum of tensor subspaces can be given a ring structure with the help of direct tensor product in the following symbolic notation:
 (2)
(2)
where 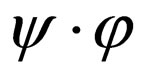 is an inner product or convolution that decreases the number of basis vectors and
is an inner product or convolution that decreases the number of basis vectors and  is external product that increase number of basis vectors. If every Clifford number multiple on special fixed matrix, which have one own column with elements own and other zero we can obtain the Dirac spinor with four element. With the help this column can reproduce spinor presentation every Clifford number. Exist full correspondence between the spinor column and the elements of an exterior algebra.
is external product that increase number of basis vectors. If every Clifford number multiple on special fixed matrix, which have one own column with elements own and other zero we can obtain the Dirac spinor with four element. With the help this column can reproduce spinor presentation every Clifford number. Exist full correspondence between the spinor column and the elements of an exterior algebra.
Next we would like determine the rule of comparing two Clifford number in different point of manifold. For this goal should be determine the deformation of coordinate system and rule of parallel displacement on different manifold. An arbitrary deformation of the coordinate system can be set in terms of basis deformations , where X is the Clifford number that describes arbitrary changes of the basis (including arbitrary displacements and rotations) which do not violate its normalization, i.e., provided
, where X is the Clifford number that describes arbitrary changes of the basis (including arbitrary displacements and rotations) which do not violate its normalization, i.e., provided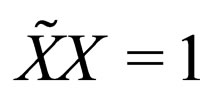 . It is not difficult to verify that
. It is not difficult to verify that  and this does not violate the normalization of the basis [5]. Now, for an arbitrary basis, we can set, at each point of the space, a unique complete linearly independent form as a geometric entity that characterizes this point of the manifold. For a four-dimensional space, such geometric entity may be given by
and this does not violate the normalization of the basis [5]. Now, for an arbitrary basis, we can set, at each point of the space, a unique complete linearly independent form as a geometric entity that characterizes this point of the manifold. For a four-dimensional space, such geometric entity may be given by
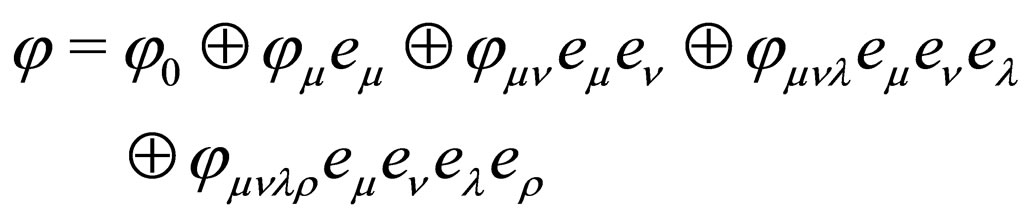 (3)
(3)
If this point of the manifold is occupied by an elementary particle, then its geometric characteristics may be described by the coefficients of this representation. A product of arbitrary forms of this type is given by a similar form with new coefficients, thus providing the ring structure. This approach makes it possible to consider the mutual relation of fields of different physical nature [13,14]. However, in what follows we consider new concept to description of a particle and characteristic of manifold as a geometric entity.
Defining a single characteristic of manifold as a point function means associating each point of manifold with a rial number, determined by the function value. If the function is differentiable with respect to its argument, then we have differentiation of present form. In order to determine the operation of form translation over an arbitrary manifold we have to define the derivative operation. It may written as a linear form  where
where 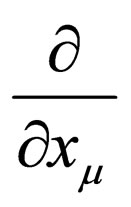 that forms a basis of the vector space of all changes along the curves passing through a given individual point of the space. The action of such an operator on an arbitrary form may be presented as
that forms a basis of the vector space of all changes along the curves passing through a given individual point of the space. The action of such an operator on an arbitrary form may be presented as
 (4)
(4)
where  and
and  may be called the “divergence” and the “curl” of the relevant form, according to the definition of the differentiable variety, it is insufficient to have one non-singular coordinate system to cover a manifold the topology of which differs from the topology of an open set in the Euclidian space. The structure of such geometric construction should be complemented with a correlation between the values of the transferred forms in different points of the manifold. When assigning intrinsic values to the manifold characteristics, it is necessary to introduce the low of form transformation with the change of the coordinate system. Manifold mapping is defined through mapping of corresponding system of the form which a certain group Li causes to transform. A possible transformation of any geometric characteristic which caused both by the turn of a corresponding coordinate system as well as by the transformation of the geometric entity themselves, requires the use of Clifford algebra upon the elements of the inner vector space group (simplectic group
may be called the “divergence” and the “curl” of the relevant form, according to the definition of the differentiable variety, it is insufficient to have one non-singular coordinate system to cover a manifold the topology of which differs from the topology of an open set in the Euclidian space. The structure of such geometric construction should be complemented with a correlation between the values of the transferred forms in different points of the manifold. When assigning intrinsic values to the manifold characteristics, it is necessary to introduce the low of form transformation with the change of the coordinate system. Manifold mapping is defined through mapping of corresponding system of the form which a certain group Li causes to transform. A possible transformation of any geometric characteristic which caused both by the turn of a corresponding coordinate system as well as by the transformation of the geometric entity themselves, requires the use of Clifford algebra upon the elements of the inner vector space group (simplectic group ).
).
 (5)
(5)
where X, Y, Z have representation, constructed with the elements of the simplectic group and analogous to those of original form, while f are structural constant, depend on the manifold point, they are represented by tensor values of all dimensional determined by the initial vector space. A certain transformation group transforms each form according to the law
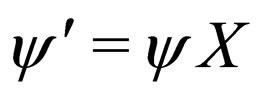 (6)
(6)
where X determines the mapping elements, of Clifford algebra in our case, and satisfies the condition XX = 1. For this algebra, we can write the first structure equation that defines the co-variant derivative as given by [13]:
 (7)
(7)
with the gauge transformation law for the constraint 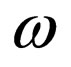 being given by
being given by
 (8)
(8)
for the conservation co-variant transformation according to the same law . Here the tensor representation of the constraint is similar to that of an arbitrary form of the Clifford algebra. The present equation called the first structural equation but now the form will assume the value in Clifford algebra. In this case the arbitrary Clifford number can always be reduced to the canonical form, but local deformations of the proper basis become, however, is not observable since the Tetroude form
. Here the tensor representation of the constraint is similar to that of an arbitrary form of the Clifford algebra. The present equation called the first structural equation but now the form will assume the value in Clifford algebra. In this case the arbitrary Clifford number can always be reduced to the canonical form, but local deformations of the proper basis become, however, is not observable since the Tetroude form  corresponds to the second term of the gauge transformation. Then the second structure equation that defines the “curvature” form may be written as
corresponds to the second term of the gauge transformation. Then the second structure equation that defines the “curvature” form may be written as
 (9)
(9)
with the law of transformation under the algebra being given by . The transfer equation for the curvature tensor with the present transformation law can written in the following form
. The transfer equation for the curvature tensor with the present transformation law can written in the following form
 (10)
(10)
where J is the source form with the analogous general representation which complies the transformation  . The obtained equation can be regarded as field equation, its form externally similar to analogous equation for the connectivity form obtained in Li algebra. Those equations have a more general character as their structure contains interrelation of geometric characteristic whose tensor nature is different. In this presentation can be written the fourth structural equation which demonstrates the dependence between covariant derivation and form curvature:
. The obtained equation can be regarded as field equation, its form externally similar to analogous equation for the connectivity form obtained in Li algebra. Those equations have a more general character as their structure contains interrelation of geometric characteristic whose tensor nature is different. In this presentation can be written the fourth structural equation which demonstrates the dependence between covariant derivation and form curvature:
 (11)
(11)
We can assume that the every elementary particle in every point of manifold can describe in the term Clifford number. Then the particle wave function is represented by a complete geometric entity—a sum of probable direct forms of an induced space of the Clifford algebra. Moreover, having attributed the wave function with geometrical sense we can obtain correct translation rules for an arbitrary manifold [13] and come to some new quantum results associated with the geometric nature of the wave function. For wave function as geometrical entity can write the first structural equation in the standard form:
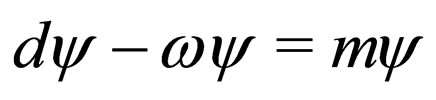 (12)
(12)
if suppose that the covariant derivation proportional same wave function as  where m is mass coefficient. The form of this equation is analogous to the Dirac equation in the spinor representation. Among these results we indicate the observation that Dirac equation in the geometric representation is nothing but the translation equation in the general relativity sense, hence its solutions may be interpreted geometrically. Moreover, the geometric representation of the wave function yields other results concerning the interference of elementary particles which just may reveal the geometric nature of the wave function [15].
where m is mass coefficient. The form of this equation is analogous to the Dirac equation in the spinor representation. Among these results we indicate the observation that Dirac equation in the geometric representation is nothing but the translation equation in the general relativity sense, hence its solutions may be interpreted geometrically. Moreover, the geometric representation of the wave function yields other results concerning the interference of elementary particles which just may reveal the geometric nature of the wave function [15].
This equation is more informative for several reasons. The first one is that spinors are only special projections of Clifford numbers [5], Dirac spinors are represented only by ideals in this algebra, and thus it is impossible to introduce the composition operation on the spinor set. And the most important difference is that complete group of linear transformations of the coordinate system does not exist for spinors [3]. As follows from the previous analysis, a complete transformation group associated with the structure equation exists only in the Cliffordnumber representation of the wave function. The first structure equation for the wave function reproduces the form of the Dirac equation and, as it has been shown in [5], its solutions are similar to those for the spinor representation. This solves the problem of finite-dimensional representation of the wave function under the complete linear group of coordinate transformations. The Dirac equation for wave function can be obtained minimize the action, constructed from geometrical invariants
 .
.
The Lagrange multiplier m ensure the normalization condition for wave function . The present action non degeneracy on the solution of Dirac equation in contrast with standard approach. In our approach the dynamic equation for wave function is presented as rule the parallel translation for characteristic of elementary particle on the arbitrary manifold. As proof in [5] the each even number
. The present action non degeneracy on the solution of Dirac equation in contrast with standard approach. In our approach the dynamic equation for wave function is presented as rule the parallel translation for characteristic of elementary particle on the arbitrary manifold. As proof in [5] the each even number 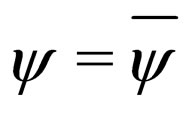 for
for , the Clifford number in Euclidean space may be reduced to the canonical form, i.e.,
, the Clifford number in Euclidean space may be reduced to the canonical form, i.e.,
 (13)
(13)
where  describes all the coordinate transformations associated with the translation and rotation of coordinates and with the Lorentz transformation in the Euclidean space. As simple to see
describes all the coordinate transformations associated with the translation and rotation of coordinates and with the Lorentz transformation in the Euclidean space. As simple to see 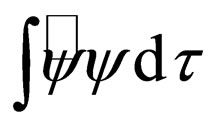 is scalar and in the physical interpretation of this geometric entity is rather evident since
is scalar and in the physical interpretation of this geometric entity is rather evident since  can be associated with the probability density of finding a particle in an arbitrary spatial point, and
can be associated with the probability density of finding a particle in an arbitrary spatial point, and  is the angle that determines the eigenvalue of a particle with positive or negative energy. We can take
is the angle that determines the eigenvalue of a particle with positive or negative energy. We can take  for an electron and
for an electron and  for a positron. Thus it becomes possible to describe the intermediate states of the particle since the form of the wave function of an arbitrary ensemble of particles is analogous [7]. As proof in the book [5] the odd part of general Clifford number can present as even part which multiplied on the isolate element of this algebra γ0 and thus not problem with manipulation of full Clifford number. The structure equation thus obtained is written in the introduced terms is completely equivalent to the Dirac equation, and has well known solutions both for the calculation of the hydrogen atom spectrum and for the interpretation of electron states [5].
for a positron. Thus it becomes possible to describe the intermediate states of the particle since the form of the wave function of an arbitrary ensemble of particles is analogous [7]. As proof in the book [5] the odd part of general Clifford number can present as even part which multiplied on the isolate element of this algebra γ0 and thus not problem with manipulation of full Clifford number. The structure equation thus obtained is written in the introduced terms is completely equivalent to the Dirac equation, and has well known solutions both for the calculation of the hydrogen atom spectrum and for the interpretation of electron states [5].
3. Experimental Determination of Geometric Entity
General problem consist to experimental observation geometrical presentation of wave function. Usually, that in general relativity the geometrical presentation of wave function should be crucial role and will be observed for many cases. But we would like suggest on possibility to determine geometrical character of wave function which relate to modern real condition. We consider the case of particle diffraction on two holes that might be helpful in revealing the geometric character of the wave function. In our representation, two possible passing the one particle can be described by the wave functions represented by geometric entities in the canonical form, i.e.,

and  .
.
For electrons we have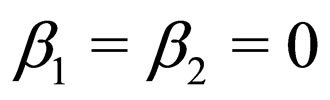 . The canonical form of the interference two possible passing of the wave function of electron should be similar, i.e.,
. The canonical form of the interference two possible passing of the wave function of electron should be similar, i.e.,
 .
.
Now the post-interference result can be written as
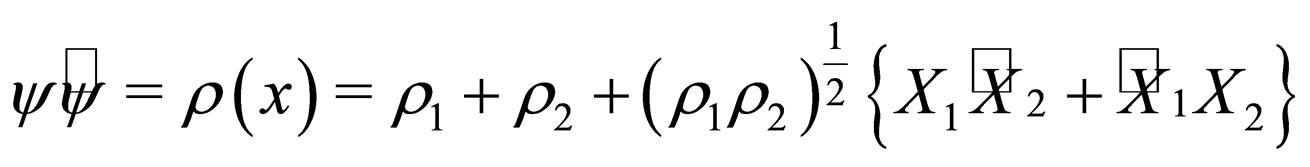 (14)
(14)
In the case of even Clifford numbers, when X corresponds to Lorentz rotations, i.e., when  can be written as
can be written as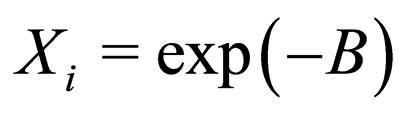 , where
, where  is a double vector,
is a double vector,  and
and  are constant numbers, and b is a vector whose modulus is equal to one, the result of interference, is given by the standard expression, i.e.,
are constant numbers, and b is a vector whose modulus is equal to one, the result of interference, is given by the standard expression, i.e.,
 (15)
(15)
For plane monochromatic waves [5], the solution of the Dirac equation is given by
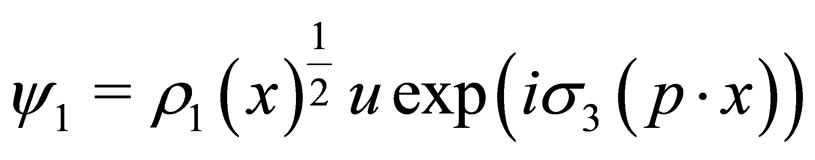
where  is the Pauli matrix, u is particle amplitude, and p is particle momentum. The second solution is similar except for the phase shift, i.e., we have
is the Pauli matrix, u is particle amplitude, and p is particle momentum. The second solution is similar except for the phase shift, i.e., we have
 .
.
We see that now electron interference is described by the well known formula.
Next we assume that deformations of the reference system can change the geometrical entity and can give the result, which principal are different as standard approach. The existence of this effect can be verified experimentally. A coherent electron beam should be divided into two beams, the latter should be passed through separate regions with variable basic geometric characteristics. The change of the wave function passing through different regions can be written as  where
where  and
and 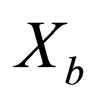 describe the transformation of particle characteristics in the regions a and b. If the sequence order is changed,
describe the transformation of particle characteristics in the regions a and b. If the sequence order is changed, 
 then electron interference should correspond to the last case of the previous analysis, i.e., the interference pattern should be different from the standard case. The various regions can be infinite solenoids of the Aaronov-Bohm experiment with different directions of the magnetic flux. If change the direction of the magnetic flux in two solenoids we can observe the different interference picture, which will be different as standard. Another way to observe the difference of the interference patterns is to pass electrons along and across the solenoids. The difference is given rise to only by the geometric representation since in the first case the flux is not changed as distinct to the opposite case. We can assume that this effect might be also observed for neutron interference, the regions of variation of the wave function geometric components being two inclusions with different mass numbers occurring on the neutron propagation path. A similar experiment had been proposed in paper [15], however, it has not been performed till now.
then electron interference should correspond to the last case of the previous analysis, i.e., the interference pattern should be different from the standard case. The various regions can be infinite solenoids of the Aaronov-Bohm experiment with different directions of the magnetic flux. If change the direction of the magnetic flux in two solenoids we can observe the different interference picture, which will be different as standard. Another way to observe the difference of the interference patterns is to pass electrons along and across the solenoids. The difference is given rise to only by the geometric representation since in the first case the flux is not changed as distinct to the opposite case. We can assume that this effect might be also observed for neutron interference, the regions of variation of the wave function geometric components being two inclusions with different mass numbers occurring on the neutron propagation path. A similar experiment had been proposed in paper [15], however, it has not been performed till now.
4. Conclusions
We can assume that the Clifford algebraic formalism is completely equivalent to the conventional approach to quantum mechanics. Quantum mechanics holds about the basic phenomenon of quantum interference. The first structure equation is written in the introduced geometrical terms is completely equivalent to the Dirac equation, and has well known solutions both for the calculation of the hydrogen atom spectrum and for the interpretation of electron states [5]. We may realize it using the basic elements, and the structure of the Clifford algebra. This open up the possibility of a different interpretation an explanation of quantum phenomena in term of a noncommutative geometry and predict the new experiment for determination geometrical presentation of wave function for elementary particle. We have to consider the basic foundations of quantum mechanics as basic framework representing conceptual entities [8].
I would like to thank Prof. J. Klauder for very useful discussion.