Traffic Flow Merging and Bifurcating at Junction on Two-Lane Highway ()
1. Introduction
Mobility is nowadays one of the most significant ingredients of a modern society. Interchanges, junctions, and on ramp prevent mobility highly. Traffic networks often exceed the capacity. The traffic congestion often occurs in city traffic networks. Traffic flow is a self-driven many-particle system of strongly interacting vehicles [1-5]. The concepts and techniques of physics are applied to such complex systems as transportation systems. Several physical models have been applied to the vehicular flow [6-28]. The dynamical phase transitions such the jamming transitions between distinct traffic states have been studied from a point of view of statistical physics and nonlinear dynamics.
Traffic jams are a typical signature of the complex behavior of traffic flow. Traffic jams are classified into two kinds of jams: 1) spontaneous jam (or phantom jam) which propagates backward as the stopand go-wave and 2) stationary jam which is induced by slowdown or blockage at a section of roadway. If a sensitivity of driver is lower than a critical value, the spontaneous jam occurs. The jamming transition is very similar to the conventional phase transitions and critical phenomena [1,15]. When the sensitivity is higher than the critical value, the spontaneous jam does not appear, while the stationary jam induced by slowdown occurs [1,26].
Nagatani [25] and Hananura et al. [26] showed that the traffic flow on a highway with bottlenecks can be modeled by introducing the slowdown section into the highway. The bottleneck corresponds to the slowdown section where the maximal velocity in the optimal velocity function is reduced and less than that at the normal section. The stationary jam is formed just before the slowdown section. The vehicular traffic with slowdown section is similar to the synchronized traffic in the threephase theory. The extension of the optimal velocity model taken into account the slowdown corresponds to the nonunique case. By introducing the slowdown section instead of the bottleneck on a highway, one will be able to model the real traffic using the extended version of optimal velocity model.
In this paper, we introduce the slowdown and weaving sections instead of the bottleneck. Therefore, the bottleneck effect on the traffic flow is taken into account in our model.
In real traffic on toll roads, manual tollgates induce frequently the queuing just in front of traditional tollbooths because the delay occurs by collecting tolls manually (with cash). The electronic toll collection system (ETC) has been used to avoid the delay by the traditional tollgates on toll road. ETC operates together with traditional tollbooths. Very recently, the dynamic model has been presented for the traffic flow of electronicand manual-collection vehicles on a toll highway with electronic and manual tollgates. The traffic behavior has been studied for the toll highway with ETC and manual tollgates [27].
In real traffic, heavy congestion frequently occurs at the junction on a highway. Vehicles change their direction at the junction by changing to the other lane. The merging and bifurcating traffic flow is called weaving. When vehicles change their lane at the weaving section of junction, they slow down. The lane changing becomes easy by the slowdown because the speed is slower, the headway necessary for changing the lane is shorter. Also, the slowdown is stronger, the traffic is more congested at the junction. Thus, traffic congestion is induced by the slowdown when vehicles move aside on the other lane for changing their direction. There exist a few works for the weaving traffic flow at the junction on a highway [28-30]. Nishi et al. have studied the effect of vehicular configuration on the weaving traffic flow on a two-lane highway by using the cellular automaton model [28]. However, the slowdown effect on the weaving traffic flow has little been studied. At the junction, the traffic behavior changes with varying the fraction of vehicles changing their direction. It is little known how the fraction of vehicles changing their direction affect the fundamental diagram and traffic states.
Weaving traffic is a combined system of the traffic flow with off and on ramps. In the weaving section on a highway, traffic behaviors observed in offand on-ramps traffic occur simultaneously because inflow and outflow occurs simultaneously on each lane. Therefore, the weaving traffic in the present work is definitely different from off-ramp traffic or from on-ramp traffic. However, the present work for weaving traffic may be related to the congestion caused by isolated off ramp or on ramp if one is able to combine the on-ramp traffic with the off-ramp traffic.
In this paper, we present the dynamic model for the weaving traffic flow at the junction on a two-lane highway. The optimal-velocity model is applied to the weaving traffic flow on a two-lane highway. Then we study the traffic states and jams induced by the weaving at the junction on the two-lane highway. The dynamical states of weaving traffic flow are clarified. The fundamental diagrams for the weaving traffic on the two-lane highway are derived.
2. Model
We consider the situation such that many vehicles move ahead through a merging and bifurcating junction on a two-lane highway. Vehicles change their lane at the weaving section of the junction for changing their direction. We mimic the weaving traffic flow at the junction on the two-lane highway. There are two kinds of vehicles: the one is A-bound vehicle and the other B-bound vehicle. A-bound vehicles on lane 1 go ahead to A direction without changing their lane. B-bound vehicles on lane 1 try to change their lane from lane 1 to lane 2 and wish to go ahead to B direction. B-bound vehicles on lane 2 go ahead to B direction without changing their lane. Abound vehicles on lane 2 try to change their lane from lane 2 to lane 1 and wish to go ahead to A direction. Figure 1(a) shows the schematic illustration of the weaving traffic flow through the merging junction on the twolane highway. A-bound vehicles are indicated by dark (red) color. B-bound vehicles are indicated by light (blue) color. Two kinds of vehicles enter into the merging junction together. The weaving occurs at the merging section. Vehicles move ahead by changing their lane if necessary. Vehicles slow down to change their lane when they enter into the weaving (merging) section. Figure 1(b) shows the schematic illustration of the weaving traffic flow model on the two-lane highway.
We partitioned the two-lane highway with the merging junction into four sections. Section N1 is a normal region with maximal velocity  where vehicles do not change their lane. Section S1 is a slowdown region with maximal velocity
where vehicles do not change their lane. Section S1 is a slowdown region with maximal velocity  (
( where vehicles do not change their lane but slow down. Section S2 is a weaving region with maximal velocity
where vehicles do not change their lane but slow down. Section S2 is a weaving region with maximal velocity 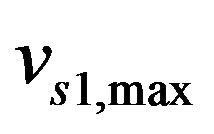 where vehicles change their lane if necessary. Section N2 is an acceleration region with maximal velocity
where vehicles change their lane if necessary. Section N2 is an acceleration region with maximal velocity  where vehicles do not change their lane but speed up. The lengths of Sections N1, S1, S2, and N2 are set as
where vehicles do not change their lane but speed up. The lengths of Sections N1, S1, S2, and N2 are set as  respectively. Two kinds of vehicles enter into the two-lane highway with mixing at a fraction. Vehicles slow down when they enter into Section S1. In Section S2, they change their lane with slowing down if necessary. After changing the lane, vehicles go ahead with accelerating.
respectively. Two kinds of vehicles enter into the two-lane highway with mixing at a fraction. Vehicles slow down when they enter into Section S1. In Section S2, they change their lane with slowing down if necessary. After changing the lane, vehicles go ahead with accelerating.
Here, traffic flow is under the periodic boundary condition. In real traffic, vehicular traffic is under the open boundary. The open boundary condition affects the traffic behavior. Also, under the open boundary conditions, it is not easy to vary the values of vehicular density. To study the effect of the vehicular density on the traffic flow, one uses the periodic boundary condition.
We assume that vehicles are forced to slow down when they enter into sections of the slowdown and weaving. When vehicles enter into the weaving section S2, vehicles change their lane if the criteria of lane changing are satisfied. The speed is lower, the lane changing is easier. At highway junctions in Japan, the slowdown region is set just before the weaving region because the lane changing is easy. Therefore, we set the slowdown section just before the weaving section. In the weaving section, vehicles slow down and change the lane. Even if there exist no slowdown section, the present simulation result is effective because vehicles slow down in the weaving section.
When a vehicle tries to take his desired route in weaving traffic, it is important that the vehicle changes the lane successfully with no collisions. When the vehicle
 (a)
(a) (b)
(b)
Figure 1. (a) Schematic illustration of the weaving traffic flow through the merging and bifurcating junction on the two-lane highway. A-bound vehicles are indicated by dark (red) color. B-bound vehicles are indicated by light (blue) color. Two kinds of vehicles enter into the junction with a mixed state. The weaving occurs at the merging section; (b) Schematic illustration of the weaving traffic flow model on the two-lane highway. We partitioned the two-lane highway with the junction into four sections.
enters into the desired lane, the vehicular speed and headway vary with time continuously. In weaving traffic, it is necessary and important that the physical quantities, space, and time are continuous variables. We prefer the differential equation model rather than the CA model. In the traffic model described in terms of the differential equation, the optimal velocity model is simple and is well studied. Therefore, we applied the optimal velocity model to the weaving traffic. Since the original optimal velocity model is an over-simplified model, we extended the original optimal velocity model to take into account the bottleneck effect (slowdown) and the lane changing.
Lane changing is implemented as a sideways movement. We assume that the vehicular movement is divided into two parts: one is the forward movement and the other is the sideways movement. We apply the optimal velocity model to the forward movement [1,15]. The optimal velocity model is described by the following equation of motion of vehicle i :
 , (1)
, (1)
where  is the optimal velocity function,
is the optimal velocity function, 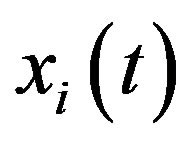 is the position of vehicle i at time t,
is the position of vehicle i at time t,
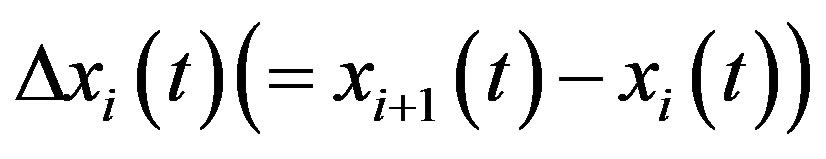 is the headway of vehicle i at time t, and
is the headway of vehicle i at time t, and  is the sensitivity (the inverse of the delay time) [1].
is the sensitivity (the inverse of the delay time) [1].
A driver adjusts the vehicular speed to approach the optimal velocity determined by the observed headway. The sensitivity  allows for the time lag
allows for the time lag  that it takes the vehicular speed to reach the optimal velocity when the traffic is varying. Generally, it is necessary that the optimal velocity function has the following properties: it is a monotonically increasing function and it has an upper bound (maximal velocity). The vehicle length is taken to be zero.
that it takes the vehicular speed to reach the optimal velocity when the traffic is varying. Generally, it is necessary that the optimal velocity function has the following properties: it is a monotonically increasing function and it has an upper bound (maximal velocity). The vehicle length is taken to be zero.
Vehicles move with the normal velocity except for the slowdown sections. In the region of normal-speed section, the optimal velocity function of vehicles is given by
 , (2)
, (2)
where  is the maximal velocity of vehicles on the roadway except for the slowdown sections and
is the maximal velocity of vehicles on the roadway except for the slowdown sections and  the position of turning point [1].
the position of turning point [1].
In the slowdown Section S1 and weaving Section S2, vehicles move with the forced speed and the vehicular velocity should be lower than the speed limits of slowdown. When vehicles enter into the slowdown and weaving sections, they obey the conventional optimal-velocity function with speed limit :
:
 , (3)
, (3)
where  is the speed limit of slowdown and weaving sections,
is the speed limit of slowdown and weaving sections, 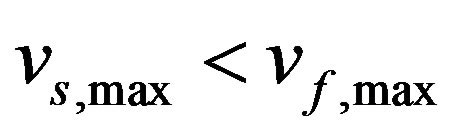 , and
, and  the position of turning point.
the position of turning point.
We consider the criteria for the lane changing. A driver of A-bound (B-bound) vehicle on the first (second) lane goes ahead on lane 1 (lane 2) without changing lane. A driver of A-bound (B-bound) vehicle on the second (first) lane change to the first (second) lane if the security criterion is satisfied. The security criterion is necessary to avoid the collision with the vehicles ahead or behind. The space between vehicles ahead and behind should be sufficiently large not to collide with the vehicles ahead and behind. The space is proportional to the maximal velocity. We propose the following security criterion. When the headway between his vehicle and the front vehicle on the target lane is larger than the prescribed distance and the headway between his vehicle and the back vehicle on the target lane is larger than the prescribed distance, it is successful for his vehicle to change the lane. We set the prescribed distance as .
.
We adopt the following lane changing rule for the two-lane highway:
 and
and 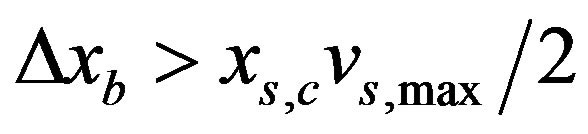
for the security criterion, (4)
where  is the headway between vehicle i and the vehicle ahead on the target lane and
is the headway between vehicle i and the vehicle ahead on the target lane and  is the headway between vehicle i and the vehicle behind on the target lane. Figure 2(a) shows the schematic illustration of lane changing. After changing lane, the vehicle shifts just to the side in Figure 2(a).
is the headway between vehicle i and the vehicle behind on the target lane. Figure 2(a) shows the schematic illustration of lane changing. After changing lane, the vehicle shifts just to the side in Figure 2(a).
If the security criterion (4) is not satisfied, the following security rule is applied because the vehicle accelerates or decelerates for changing lane:
 for the security condition. (5)
for the security condition. (5)
Figure 2(b) shows the schematic illustration of lane changing. After changing lane, the vehicular position on the target lane changes to the following: